第5章特殊的平行四边形单元检测试卷B

浙教版八年级下第5章特殊的平行四边形单元检测试卷B
班级_____________考号______________姓名_______________总分_________________
一、选择题（10小题，每题3分，共30分)
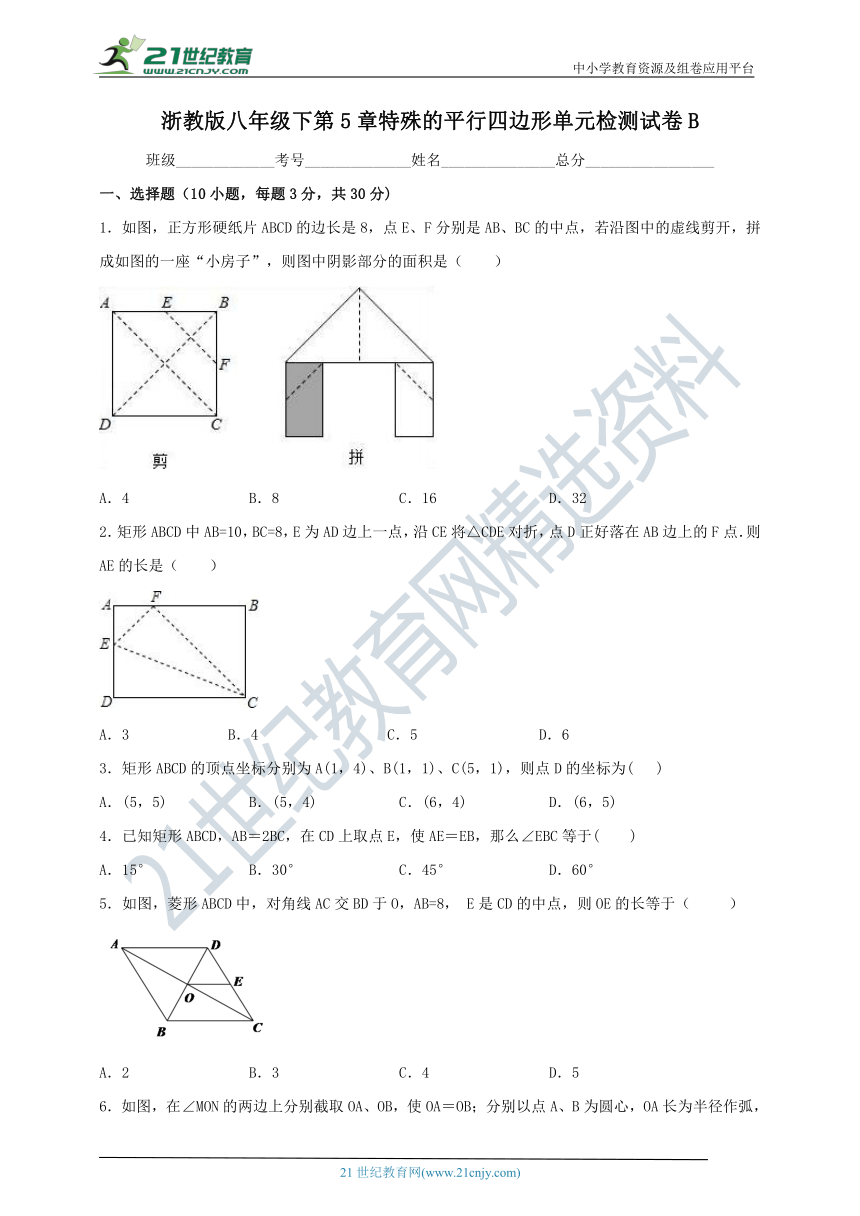
1．如图，正方形硬纸片ABCD的边长是8，点E、F分别是AB、BC的中点，若沿图中的虚线剪开，拼成如图的一座“小房子”，则图中阴影部分的面积是（　　）
A．4 B．8 C．16 D．32
2．矩形ABCD中AB=10，BC=8，E为AD边上一点，沿CE将△CDE对折，点D正好落在AB边上的F点．则AE的长是（　　）
A．3 B．4 C．5 D．6
3．矩形ABCD的顶点坐标分别为A(1，4)、B(1，1)、C(5，1)，则点D的坐标为( )
A．(5，5) B．(5，4) C．(6，4) D．(6，5)
4．已知矩形ABCD，AB＝2BC，在CD上取点E，使AE＝EB，那么∠EBC等于(　　)
A．15° B．30° C．45° D．60°
5．如图，菱形ABCD中，对角线AC交BD于O，AB=8， E是CD的中点，则OE的长等于（ ）
A．2 B．3 C．4 D．5
6．如图，在∠MON的两边上分别截取OA、OB，使OA＝OB；分别以点A、B为圆心，OA长为半径作弧，两弧交于点C；连接AC、BC、AB、OC．若AB＝2cm，四边形OACB的面积为4cm2．则OC的长为(　　)
A．2 B．3 C．4 D．5
7．如图，四边形内有一点，，，若，则的大小是（ ）
A． B． C． D．
8．如图，从下列四个条件①AB＝BC，②AC⊥BD，③∠ABC＝90°，④AC＝BD中选两个作为补充条件，使?ABCD成为正方形，下列四种选法错误的是（　　）
A．①② B．①③ C．②③ D．①④
9．如图，在梯形ABCD中，，，，，，则CD的长为　　
A． B．3 C． D．
10．如图，在△ABC中，AB=3，AC=4，BC=5，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为　( )
A． B． C． D．
二、填空题（8小题，每题3分，共24分)
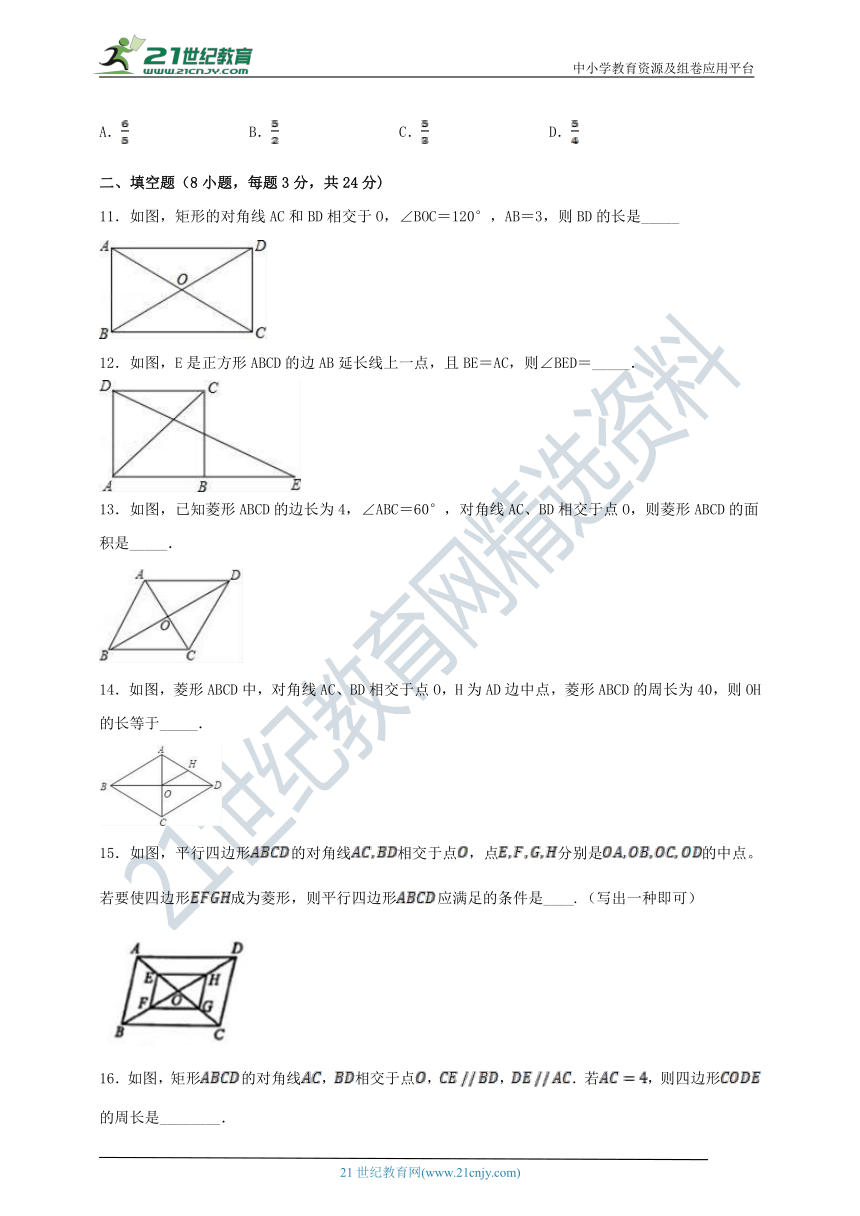
11．如图，矩形的对角线AC和BD相交于O，∠BOC＝120°，AB＝3，则BD的长是_____
12．如图，E是正方形ABCD的边AB延长线上一点，且BE＝AC，则∠BED＝_____．
13．如图，已知菱形ABCD的边长为4，∠ABC＝60°，对角线AC、BD相交于点O，则菱形ABCD的面积是_____．
14．如图，菱形ABCD中，对角线AC、BD相交于点O，H为AD边中点，菱形ABCD的周长为40，则OH的长等于_____．
15．如图，平行四边形的对角线相交于点，点分别是的中点。若要使四边形成为菱形，则平行四边形应满足的条件是____.（写出一种即可）
16．如图，矩形的对角线，相交于点，，．若，则四边形的周长是________．
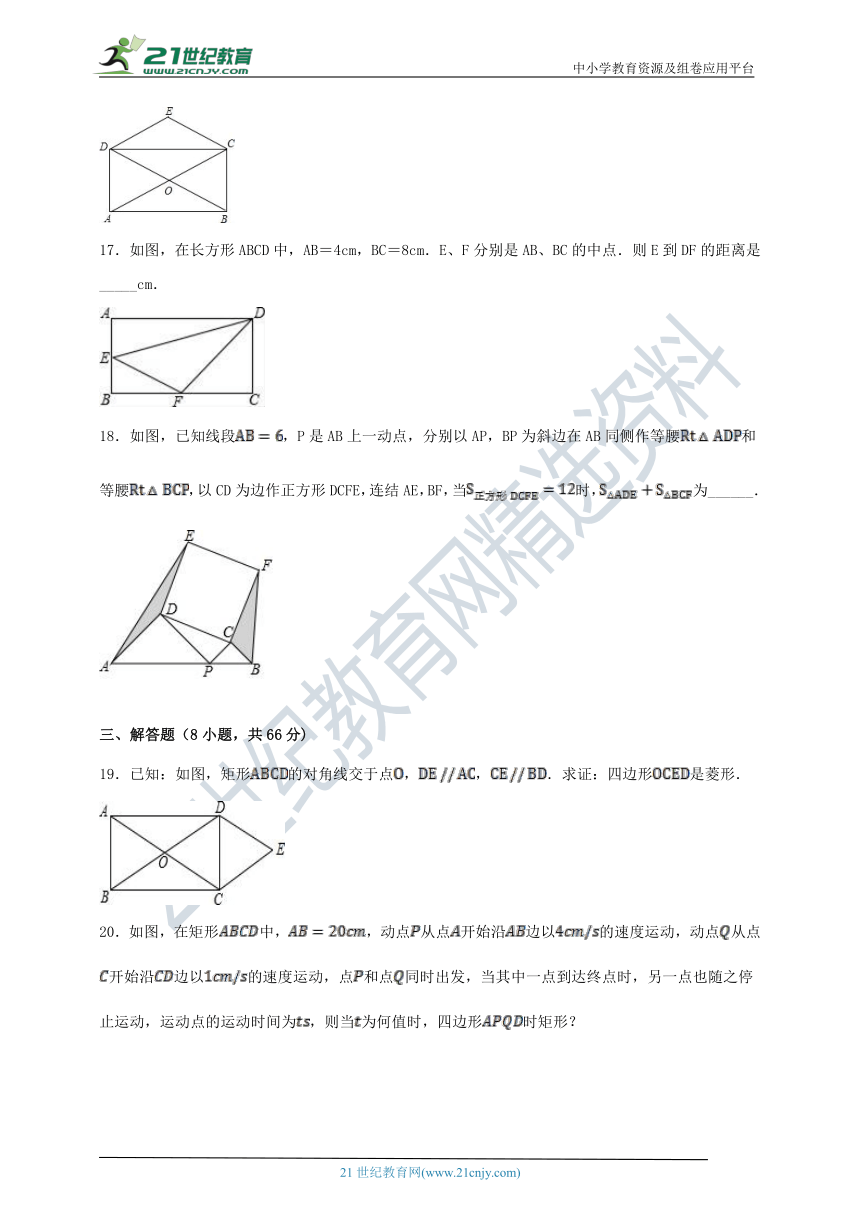
17．如图，在长方形ABCD中，AB＝4cm，BC＝8cm．E、F分别是AB、BC的中点．则E到DF的距离是_____cm．
18．如图，已知线段，P是AB上一动点，分别以AP，BP为斜边在AB同侧作等腰和等腰，以CD为边作正方形DCFE，连结AE，BF，当时，为______．
三、解答题（8小题，共66分)
19．已知：如图，矩形的对角线交于点，，．求证：四边形是菱形．
20．如图，在矩形中，，动点从点开始沿边以的速度运动，动点从点开始沿边以的速度运动，点和点同时出发，当其中一点到达终点时，另一点也随之停止运动，运动点的运动时间为，则当为何值时，四边形时矩形？
21．如图，在正方形ABCD的对角线AC上取一点E，使CE＝CD，过点E作EF⊥AC交AD于点F.
求证：AE＝EF＝DF.
22．已知平行四边形ABCD中，对角线AC和BD相交于点O，AC＝10，BD＝8．
(1)若AC⊥BD，试求四边形ABCD的面积；
(2)若AC与BD的夹角∠AOD＝60°，求四边形ABCD的面积．
23．如图，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA＝PE，PE交CD于F.
(1)证明：PC＝PE；
(2)求∠CPE的度数．
24．如图，矩形ABCD的对角线AC的中点为O，过点O作，交BC边于点E，交AD边于点F，分别连接AE、CF．
求证：四边形AECF是菱形；
若，，请直接写出EF的长为______．
25．小儒在学习了定理“直角三角形斜边上的中线等于斜边的一半”之后做了如下思考：
（1）他认为该定理有逆定理，即“如果一个三角形某条边上的中线等于该边长的一半，那么这个三角形是直角三角形”应该成立，你能帮小儒证明一下吗？如图①，在△ABC中，AD是BC边上的中线，若AD＝BD＝CD，求证：∠BAC＝90°．
（2）接下来，小儒又遇到一个问题：如图②，已知矩形ABCD，如果在矩形外存在一点E，使得AE⊥CE，求证：BE⊥DE，请你作出证明，可以直接用到第（1）问的结论．
（3）在第（2）问的条件下，如果△AED恰好是等边三角形，直接用等式表示出此时矩形的两条邻边AB与BC的数量关系．
26．在矩形ABCD中，AB=4，BC=8，经过对角线交点O的直线EF绕点O旋转，分别交AD、BC于点E、F，连接AF、CE．
（1）如图（1），依据下列条件在普通四边形、梯形、普通平行四边形、矩形、菱形或正方形中选择填空：①旋转过程中四边形AFCE始终为________；
②当点E为AD的中点时四边形AFCE为_______；
③当EF⊥AC时四边形AFCE为________；
（2）如图（1），当EF⊥AC时，求AF的长；
（3）如图（2），在（2）的基础上，若动点P从A点出发，沿A→F→B→A运动一周停止，速度为每秒5cm；同时点Q从C点出发，沿C→D→E→C运动一周停止，速度为每秒4cm，在P、Q运动过程中，第几秒时，四边形APCQ是平行四边形？
参考答案
1．【考点】正方形的性质
【分析】根据阴影部分的组成与原正方形面积之间的关系解答．
解：阴影部分由一个等腰直角三角形和一个直角梯形组成，
由第一个图形可知：阴影部分的两部分可构成正方形的四分之一，
正方形的面积=8×8=64，
∴图中阴影部分的面积是64÷4=16．
故选：C．
【点睛】此题考查了剪纸问题．注意得到阴影部分面积与原正方形面积的关系是解决本题的突破点．
2．【考点】翻折变换，矩形的性质，勾股定理
【分析】由矩形的性质和折叠的性质可得CF=DC=10，DE=EF，由勾股定理可求BF的长，即可得AF=4，在Rt△AEF中，由勾股定理即可求得AE的长．
解：∵四边形ABCD是矩形，
∴AB=CD=10，BC=AD=8，∠A=∠D=∠B=90°，
∵折叠，
∴CD=CF=10，EF=DE，
在Rt△BCF中，BF==6，
∴AF=AB-BF=10-6=4，
在Rt△AEF中，AE2+AF2=EF2，
∴AE2+16=(8-AE)2，
∴AE=3，
故选A．
【点睛】本题考查了翻折变换，矩形的性质，勾股定理，熟练掌握折叠的性质是本题的关键．
3．【考点】矩形的性质，坐标与图形性质
【分析】由矩形的性质可得AB∥CD，AB=CD，AD=BC，AD∥BC，即可求点D坐标．
解：∵四边形ABCD是矩形∴AB∥CD，AB=CD，AD=BC，AD∥BC，∵A（1，4）、B（1，1）、C（5，1），∴AB∥CD∥y轴，AD∥BC∥x轴∴点D坐标为（5，4）故选：B．
【点睛】本题考查了矩形的性质，坐标与图形性质，关键是熟练掌握这些性质.
4．【考点】矩形性质，三角形的内角和定理，平行线性质，等腰三角形的性质，含30度角的直角三角形
【分析】根据矩形性质得出∠D＝∠ABC＝90°，AD＝BC，DC∥AB，推出AE＝2AD，得出∠DEA＝30°＝∠EAB，求出∠EBA的度数，即可求出答案．
解：如图：
∵四边形ABCD是矩形，
∴∠D＝∠ABC＝90°，AD＝BC，DC∥AB，
∵AB＝AE，AB＝2CB，
∴AE＝2AD，
∴∠DEA＝30°，
∵DC∥AB，
∴∠DEA＝∠EAB＝30°，
∵AE＝AB，
∴∠ABE＝∠AEB＝（180°﹣∠EAB）＝75°，
∵∠ABC＝90°，
∴∠EBC＝90°﹣75°＝15°，
故选：A．
【点睛】本题考查了矩形性质，三角形的内角和定理，平行线性质，等腰三角形的性质，含30度角的直角三角形性质的应用，解此题的关键是求出∠ABC和∠EBA的度数．
5．【考点】菱形的性质，三角形的中位线定理
【分析】根据菱形的性质得出OD=OB，根据三角形的中位线性质得出OE=AB，代入求出即可．
解：∵四边形ABCD是菱形，
∴DO=OB，
∵E是BC的中点，
∴OE=AB，
∵AB=8，
∴OE=4．
故选C．
【点睛】本题考查了菱形的性质和三角形的中位线定理的应用，关键是求出OE=AB，此题比较简单．
6．【考点】菱形的判定与性质
【分析】根据作法判定出四边形OACB是菱形，再根据菱形的面积等于对角线乘积的一半列式计算即可得解．
解：根据作图，AC＝BC＝OA，
∵OA＝OB，
∴OA＝OB＝BC＝AC，
∴四边形OACB是菱形，
∵AB＝2cm，四边形OACB的面积为4cm2，
∴AB?OC＝×2×OC＝4，
解得OC＝4cm．
故选：C．
【点睛】本题考查了菱形的判定与性质，菱形的面积等于对角线乘积的一半的性质，判定出四边形OACB是菱形是解题的关键．
7．【考点】菱形的判定与性质
【分析】由题干BE=DE=BC=DC，可知四边形BECD为菱形，又∠C=100°，所以∠BED=100°，∠CBE=∠CDE=80°．连接BD，易知AE、BE、DE是△ABD的角平分线．再根据菱形的性质即可得出答案．
解：连接BD，并延长AE交BD于点O
∵AE=BE=DE=BC=DC，AB=AD，
∴四边形BCDE是菱形，
∴AE、BE、DE是△ABD的角平分线．
∴A、E、O、C四点共线，
∵∠C=100°，∴∠BED=50°，
∴∠BEO=∠BED=50°，
∴∠ABE=25°，
∴∠BAD=50°，
故选B．
【点睛】本题主要是考查学生对三角形的性质及角平分线的灵活运用．
8．【考点】正方形的判定，矩形、菱形的判定
【分析】利用矩形、菱形、正方形之间的关系与区别，结合正方形的判定方法分别判断得出即可．
解：A、∵四边形ABCD是平行四边形，
当①AB＝BC时，平行四边形ABCD是菱形，
当②AC⊥BD时，菱形ABCD不一定正方形，故此选项错误，符合题意；
B、∵四边形ABCD是平行四边形，
当①AB＝BC时，平行四边形ABCD是菱形，
当③∠ABC＝90°时，平行四边形ABCD是正方形，故此选项正确，不符合题意；
C、∵四边形ABCD是平行四边形，
当③∠ABC＝90°时，平行四边形ABCD是矩形，
当②AC⊥BD时，菱形ABCD是正方形，故此选项正确，不合题意；
D、∵四边形ABCD是平行四边形，
∴当①AB＝BC时，平行四边形ABCD是菱形，
当④AC＝BD时，矩形ABCD是正方形，故此选项正确，不合题意，
故选A．
【点睛】本题主要考查了正方形的判定以及矩形、菱形的判定方法，正确掌握正方形的判定方法是解题关键．
9．【考点】等腰直角三角形的判定和性质，正方形的判定和性质，勾股定理
【分析】延长AD，过C作AD的延长线，垂足为过A作BC的垂线，垂足为F，已知四边形AFCE是正方形，所以，，在直角三角形DEC中，根据勾股定理，即可求出CD的值．
解：延长AD，过C作AD的延长线，垂足为过A作BC的垂线，垂足为F，
，，
三角形ABC是等腰直角三角形，
，
，四边形AFCE是正方形；
，，
，
，
在直角三角形DEC中，根据勾股定理，得到，
故选D．
【点睛】本题考查了等腰直角三角形的判定和性质、正方形的判定和性质以及勾股定理的运用，正确添加辅助线，熟练运用相关知识是解题的关键.
10．【考点】勾股定理的逆定理，矩形的判定及性质
【分析】根据勾股定理的逆定理可以证明∠BAC=90°；根据直角三角形斜边上的中线等于斜边的一半，则AMEF，要求AM的最小值，即求EF的最小值；根据三个角都是直角的四边形是矩形，得到四边形AEPF是矩形，根据矩形的对角线相等，得EF=AP，则EF的最小值即为AP的最小值，根据垂线段最短，知：AP的最小值即等于直角三角形ABC斜边上的高．
解：在△ABC中，∵AB=3，AC=4，BC=5，
∴AB2+AC2=BC2，即∠BAC=90°．
又∵PE⊥AB于E，PF⊥AC于F，
∴∠AEP=∠AFP=90°，
∴四边形AEPF是矩形，
∴EF=AP．
∵M是EF的中点，
∴AMEFAP．
因为AP的最小值即为直角三角形ABC斜边上的高，即等于，
∴AM的最小值是．
故选A．
【点睛】本题综合运用了勾股定理的逆定理、矩形的判定及性质、直角三角形的性质．要能够把要求的线段的最小值转换为便于分析其最小值的线段．
11．【考点】矩形的性质，等边三角形的判定与性质
【分析】根据矩形的性质，因为矩形的对角线相等且互相平分，则△AOB是等腰三角形．
解：∵∠BOC＝120°，
∴∠AOB＝180°﹣∠BOC＝180°﹣120°＝60°，
∵四边形ABCD是矩形，
∴AO＝BO＝OD，
∴△AOB是等边三角形，
∴AO＝OB＝AB＝3，
∴BD＝2OB＝6．
故答案为：6
【点睛】本题考查了矩形的性质，等边三角形的判定与性质，熟记各性质并判断出△AOB是等边三角形是解题的关键．
12．【考点】正方形的性质，等腰三角形的性质
【分析】首先连接BD，所以得BE＝AC＝BD，即得∠BED＝∠BDE，根据正方形的性质得∠ABD＝45°，∠BED+∠BDE＝∠ABD＝45°，从而求得∠BED．
解：连接BD，
∵正方形ABCD，AD＝AB，
∴∠ABD＝45°，
∴AC＝BD，
∵BE＝AC，
∴BE＝BD，
∴∠BED＝∠BDE，
∴∠BED+∠BDE＝∠ABD＝45°，
∴2∠BED＝45°，
∴∠BED＝22.5°，
故答案为：22.5°．
【点睛】本题考查了正方形的性质、等腰三角形底角相等的性质，根据∠BED＝∠BDE和∠BED+∠BDE＝∠ABD＝45°求∠BED是解题的关键．
13．【考点】菱形的性质
【分析】根据菱形的性质可得AO=CO，BO=DO，AC⊥BD，∠DBC=∠ABC=30°，根据直角三角形的性质可得CO=BC=2，BO=CO=2，即可求菱形ABCD的面积．
解：∵四边形ABCD是菱形，
∴AO=CO,BO=DO,AC⊥BD,∠DBC=∠ABC=30°，
∴CO=BC=2，BO=CO=2
∴AC=4，BD=4
∴S菱形ABCD=×AC×BD=
故答案为
【点睛】本题考查了利用菱形的性质求面积，熟练掌握性质是解题的关键.
14．【考点】菱形的性质，直角三角形斜边上的中线
【分析】首先求得菱形的边长，则OH是直角△AOD斜边上的中线，依据直角三角形的性质即可求解．
解：AD＝×40＝10．
∵菱形ANCD中，AC⊥BD．
∴△AOD是直角三角形，
又∵H是AD的中点，
∴OH＝AD＝×10＝5．
故答案是：5．
【点睛】本题考查了菱形的性质和直角三角形的性质，直角三角形斜边上的中线等于斜边的一半．
15． 【考点】三角形中位线，菱形的判定
【分析】根据中位线定理可得FG=BC，FG//BC，EH=AD，EH//AD，由AD//BC可证明EH//FG，EH=FG，即可证明四边形EFGH是平行四边形，根据邻边相等的平行四边形是菱形添加条件即可.
解：∵点分别是的中点，
∴FG=BC，FG//BC，EH=AD，EH//AD，EF=AB，EF//AB
∵AD//BC，
∴EH//FG，EH=FG，
∴四边形EFGH是平行四边形，
∵要使四边形成为菱形，
∴EF=FG，
∵EF=AB，FG=BC，
∴AB=BC.
∴平行四边形应满足的条件是AB=BC(答案不唯一).
故答案为：AB=BC(答案不唯一)
【点睛】本题考查三角形中位线的性质及菱形的判定，三角形的中位线平行于底边，且等于底边的一半；熟练掌握相关性质及定理是解题关键.
16．【考点】菱形的判定与性质，矩形的性质
【分析】先证明四边形CODE是平行四边形，再根据矩形的性质得出OC=OD，然后证明四边形CODE是菱形，即可求出周长．
解：∵CE∥BD，DE∥AC，
∴四边形CODE是平行四边形，
∵四边形ABCD是矩形，
∴OC=AC=2，OD=BD，AC=BD，
∴OC=OD=2，
∴四边形CODE是菱形，
∴DE=CE=OC=OD=2，
∴四边形CODE的周长=2×4=8；
故答案为：8．
【点睛】本题考查了菱形的判定与性质以及矩形的性质；证明四边形是菱形是解决问题的关键．
17．【考点】矩形的性质，勾股定理，三角形面积
【分析】根据矩形的性质得出CD=AB=4cm，AD=BC=8cm，∠A=∠B=∠C=∠D=90°，由已知条件求出AE、BE、BF、CF的长，根据勾股定理求出DF，求出△DEF的面积，作EG⊥DF于G，由三角形的面积求出EG即可．
解：∵四边形ABCD是矩形，
∴CD＝AB＝4cm，AD＝BC＝8cm，∠A＝∠B＝∠C＝∠D＝90°，
∵E、F分别是AB、BC的中点，
∴AE＝BE＝ AB＝2cm，BF＝CF＝ BC＝4cm，
∴DF＝ ＝4 （cm），
∴△DEF的面积＝矩形ABCD的面积﹣△BEF的面积﹣△CDF的面积﹣△ADE的面积
＝8×4﹣ ×4×2﹣ ×4×4﹣ ×8×2
＝12（cm2），
作EG⊥DF于G，如图所示：
则△DEF的面积＝ DF?EG＝12，
∴EG＝ ＝3 （cm），
即E到DF的距离是3 cm，
故答案为：3 ．
【点睛】本题考查矩形的性质、勾股定理、三角形面积的计算；解题的关键是熟练掌握矩形的性质，并能进行推理计算．
18．【考点】正方形的性质，等腰直角三角形的性质，三角形全等的判定和性质，勾股定理
【分析】作于M，于N，EH垂直AD交AD的延长线于点H，作于K，则四边形KMNC为矩形，设，，可得，因为，可得，得，证明≌可得，同理，进而得出．
解：如图，作于M，于N，EH垂直AD交AD的延长线于点H，作于K，
则四边形KMNC为矩形，
线段，P是AB上一动点，分别以AP，BP为斜边在AB同侧作等腰和等腰，
设，，
，
，，
，
，即，
四边形CDEF为正方形，
，，
，
，
≌，
，
，
，
同理，
，
，
，
，
故答案为：3．
【点睛】本题考查正方形的性质，等腰直角三角形的性质，三角形全等的判定和性质，勾股定理，整体思想解题的关键是得出．
19．【考点】矩形的性质，菱形的判定
【分析】根据题意易证得四边形OCED是平行四边形，再根据矩形的对角线互相平分且相等求出OC=OD，然后根据一组邻边相等的平行四边形是菱形证明．
解：∵，即，
，即，
∴ 四边形是平行四边形．
又∵四边形是矩形，
∴ ，，
且，
∴．
∴四边形是菱形．
【点睛】本题主要考查矩形的性质，菱形的判定，解此题的关键在于熟练掌握其知识点.
20．【考点】矩形的判定与性质
【分析】根据题意表示出AP=4t, DQ=20-t; 根据菱形的对边相等, 求出的值, 即可解决问题.
解：
由题意得：，；
∵四边形是矩形，
∴，即，
解得：．
即当时，四边形是矩形．
【点睛】本题主要考查矩形的判定与性质.
21．【考点】正方形的性质，全等三角形的判定与性质，等腰直角三角形的判定与性质
【分析】连接CF，求证△CEF≌△CDF，可以求证EF=DF．进一步求证△AEF为等腰直角三角形，得出EF=AE，即可证得结论．
证明：如图，连接CF，在正方形ABCD中，∠D＝∠DAB＝90°，AC平分∠DAB，
∴∠DAC＝∠CAB＝45°.
又∵EF⊥AC，
∴∠DAC＝∠AFE＝45°，
∴AE＝EF.
在Rt△CEF和Rt△CDF中，
∴Rt△CEF≌Rt△CDF(HL)，
∴EF＝DF，∴AE＝EF＝DF.
【点睛】本题考查了正方形的性质，全等三角形的判定与性质，等腰直角三角形的判定与性质，连接CF，并且求证Rt△CEF≌Rt△CDF是解本题的关键．
22．【考点】平行四边形的性质，菱形的性质和判定
【分析】（1）先证平行四边形ABCD是菱形，根据菱形的面积公式即可求解；（2）过点A分别作AE⊥BD，垂足为E，根据三角函数即可求得AE的长，从而求得△OAD的面积，四边形ABCD的面积是三角形OAD的面积的4倍，据此即可求解．
解：(1)∵AC⊥BD，
∴平行四边形ABCD为菱形，
∴S菱形ABCD＝AC×BD＝40；
(2)过点A分别作AE⊥BD，垂足为E，
∵四边形ABCD为平行四边形，
∴AO＝CO＝AC＝5，BO＝DO＝BD＝4，
在Rt△AOE中，sin∠AOE＝，
∴AE＝AO?sin∠AOE＝AO×sin60°＝，
∴S四ABCD＝OD?AE×4＝×4××4＝20．
故答案为：(1)S菱形ABCD＝40；(2)S四ABCD=20 .
【点睛】本题考查平行四边形的性质，菱形的性质和判定的应用，正确理解四边形ABCD的面积是△OAD的面积的4倍是解题的关键．
23．【考点】方形的性质，全等三角形的判定与性质
【分析】（1）先利用正方形的性质得，AB=BC，∠ABD=∠CBD=45°，则根据“SAS”可判定△ABP≌△CBP，所以PA=PC，于是得到PC=PE；（2）利用△ABP≌△CBP得到∠BAP=∠BCP，根据等角的余角相等得到∠DAP=∠DCP，再利用PA=PE得到∠DAP=∠E，所以∠PCD=∠E，然后利用三角形内角和定理得到∠CPE=∠EDF=90°
(1)证明：在正方形ABCD中，AB＝BC，∠ABP＝∠CBP＝45°，
在△ABP和△CBP中，
∴△ABP≌△CBP(SAS)．∴PA＝PC.∵PA＝PE，∴PC＝PE.
(2)解：由(1)知，△ABP≌△CBP，
∴∠BAP＝∠BCP.∴∠DAP＝∠DCP.
∵PA＝PE，∴∠DAP＝∠E.∴∠DCP＝∠E.
∵∠CFP＝∠EFD(对顶角相等)，
∴180°－∠PFC－∠PCF＝180°－∠DFE－∠E.即∠CPE＝∠EDF＝90°.
【点睛】本题考查了正方形的性质、全等三角形的判定与性质定理，关键是掌握正方形的性质
24．【考点】矩形的性质，菱形的判定和性质，全等三角形的判定和性质，勾股定理
【分析】(1)由矩形的性质可得∠ACB=∠DAC，然后利用“角角边”证明△AOF和△COE全等，根据全等三角形对应边相等可得OE=OF，即可证四边形AECF是菱形；
(2)由菱形的性质可得AE=EC，AO=CO，EO=FO，由勾股定理可求CE、EO的长，即可求EF的长．
解：四边形ABCD是矩形，
，
，
是AC的中点，
，
在和中，
，
≌，
，且
四边形AECF是平行四边形，
又，
四边形AECF是菱形；
四边形AECF是菱形，
，，，
，
，
，
，，
，
故答案为：.
【点睛】本题考查了矩形的性质，菱形的判定和性质，全等三角形的判定和性质，勾股定理，熟练运用这些性质进行推理是本题的关键．
25．【考点】四边形综合题
【分析】（1）利用等腰三角形的性质和三角形内角和即可得出结论；
（2）先判断出OEAC，即可得出OEBD，即可得出结论；
（3）先判断出△ABE是底角是30°的等腰三角形，即可构造直角三角形即可得出结论．
解：（1）∵AD＝BD，
∴∠B＝∠BAD，
∵AD＝CD，
∴∠C＝∠CAD，
在△ABC中，∠B+∠C+∠BAC＝180°，
∴∠B+∠C+∠BAD+∠CAD＝∠B+∠C+∠B+∠C＝180°
∴∠B+∠C＝90°，
∴∠BAC＝90°，
（2）如图②，连接AC，BD，OE，
∵四边形ABCD是矩形，
∴OA＝OB＝OC＝ODACBD，
∵AE⊥CE，
∴∠AEC＝90°，
∴OEAC，
∴OEBD，
∴∠BED＝90°，
∴BE⊥DE；
（3）如图3，∵四边形ABCD是矩形，
∴AD＝BC，∠BAD＝90°，
∵△ADE是等边三角形，
∴AE＝AD＝BC，∠DAE＝∠AED＝60°，
由（2）知，∠BED＝90°，
∴∠BAE＝∠BEA＝30°，
过点B作BF⊥AE于F，
∴AE＝2AF，在Rt△ABF中，∠BAE＝30°，
∴AB＝2BF，AF＝BF，
∴AE＝2BF，
∴AE＝AB，
∴BC＝AB．
【点睛】此题是四边形综合题，主要考查了矩形的性质，直角三角形的性质和判定，含30°角的直角三角形的性质，三角形的内角和公式，解（1）的关键是判断出∠B＝∠BAD，解（2）的关键是判断出OEAC，解（3）的关键是判断出△ABE是底角为30°的等腰三角形，进而构造直角三角形，是一道中等难度的中考常考题．
26．【考点】四边形综合题
【分析】由AAS证明△AOE≌△COF，得出AE=CF，即可得出四边形AFCE为平行四边形；当E点为AD中点时，四边形AFCE为平行四边形；当EF⊥AC时，得出四边形AFCE为菱形；（2）根据勾股定理得出方程，解方程即可求得AF的长；（3）分情况讨论可知，P在BF上，Q在ED上时，才能构成平行四边形，根据平行四边形的性质列方程求解即可.
解：（1）①∵四边形ABCD是矩形，
∴AD∥BC，OA=OC，
∴∠CAD=∠ACB，∠AEF=∠CFE．
在△AOE和△COF中，，
∴△AOE≌△COF（AAS），
∴AE=CF．
又∵AE∥CF，
∴四边形AFCE为平行四边形；
②当点E为AD的中点时，AE=CF，AE∥CF，
则四边形AFCE为平行四边形；
③当EF⊥AC时，四边形AFCE为菱形，理由如下：
∵由①知四边形AFCE为平行四边形，
∵EF⊥AC，
∴四边形AFCE为菱形；
故答案为：平行四边形；平行四边形；菱形．
（2）设菱形的边长AF=CF=xcm，则BF=（8–x）cm，
在Rt△ABF中，AB=4cm，
由勾股定理得：AB2+BF2=AF2，即42+（8–x）2=x2，
解得：x=5，∴AF=5；
（3）根据题意得，P点AF上时，Q点CD上，此时A，C，P，Q四点不可能构成平行四边形；
同理P点AB上时，Q点DE或CE上，也不能构成平行四边形．
∴只有当P点在BF上，Q点在ED上时，才能构成平行四边形，
∴以A，C，P，Q四点为顶点的四边形是平行四边形时，PC=QA，
∵点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，
∴PC=5t，QA=12–4t，
∴5t=12–4t，
解得：t=，
∴以A，C，P，Q四点为顶点的四边形是平行四边形时，t=秒．
【点睛】此题主要考查四边形综合题，解题的关键是熟知勾股定理的应用，特殊平行四边形的判定与性质.