1.2 锐角三角函数的计算 同步练习(含答案)
文档属性
| 名称 | 1.2 锐角三角函数的计算 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 301.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-15 18:21:48 | ||
图片预览



文档简介
浙教版九年级数学下第一章解直角三角形同步练习
1.2 锐角三角函数的计算
题号
一
二
三
总分
得分
第Ⅰ卷(选择题)
评卷人
得 分
一.选择题(共10小题,3*10=30)
1.用计算器求cos 15°,正确的按键顺序是 ( )
A.
B.
C.
D.
2. Rt△ABC中,∠C=90°,tan A=,则sin B的值为 ( )
A. B. C. D.
3. 已知sinα·sin45°=,则锐角α为( )
A.30° B.60° C. 45° D.75°
4.若tan(α+10°)=1,则锐角α的度数是 ( )
A.20° B.30° C.40° D.50°
5.将一副三角尺按如图放置,则上下两块三角尺的面积比S1:S2是( ).
A.2:3 B.2:(-1) C.:2 D.2:
6.若∠A是锐角,且cosA=tan30°,则( )
A.0°<∠A<30° B.30°<∠A<45°
C.45°<∠A<60° D.60°<∠A<90°
7.如图,在矩形ABCD中,若AD=1,AB=,则该矩形的两条对角线所成的锐角是( )
A.30° B.45° C.60° D.75°
8.如图所示是一张简易活动餐桌,测得OA=OB=30cm,OC=OD=50cm,现要求桌面离地面的高度为40cm,那么两条桌脚的张角∠COD的度数大小应为( )
A.100° B.120° C.135° D.150°
9.在△ABC中,∠A,∠B都是锐角,且sinA=,cosB=,则△ABC三个角的大小关系是( )
A.∠C>∠A>∠B B.∠B<∠C<∠A
C.∠A>∠B>∠C D.∠C>∠B>∠A
10.若θ为三角形的一个锐角,且2sinθ-=0,则θ等于( )
A.30° B.45° C.60° D.75°
第Ⅱ卷(非选择题)
评卷人
得 分
二.填空题(共8小题,3*8=24)
11.在Rt△ABC中,∠C=90°,若AC=3,AB=5,则sinA=______,tanB=______
12. 已知一个小山坡的坡度为0.62,则它的坡角为______(用计算器计算,精确到1″).
13.等腰三角形的底边长为20cm,面积为cm2,则顶角为________度.
14.化简_________,______。
15.要加工形状如图的零件,根据图示尺寸(单位:mm)计算斜角α的度数为____________.(用计算器计算,精确到1″).
16.关于x的一元二次方程x2-x+sinα=0有两个相等的实数根,则锐角α=______.
17.如图,在Rt△ABC中,∠ACB=90°,点D是AB的中点,tan∠BCD=3,则sinA=______.
18. =______
评卷人
得 分
三.解答题(共7小题, 46分)
19.(6分) 计算:
(1)2cos60°+3tan30°
(2)sin260°+tan60·cos30°
(3)sin30°+cos260°- tan30°
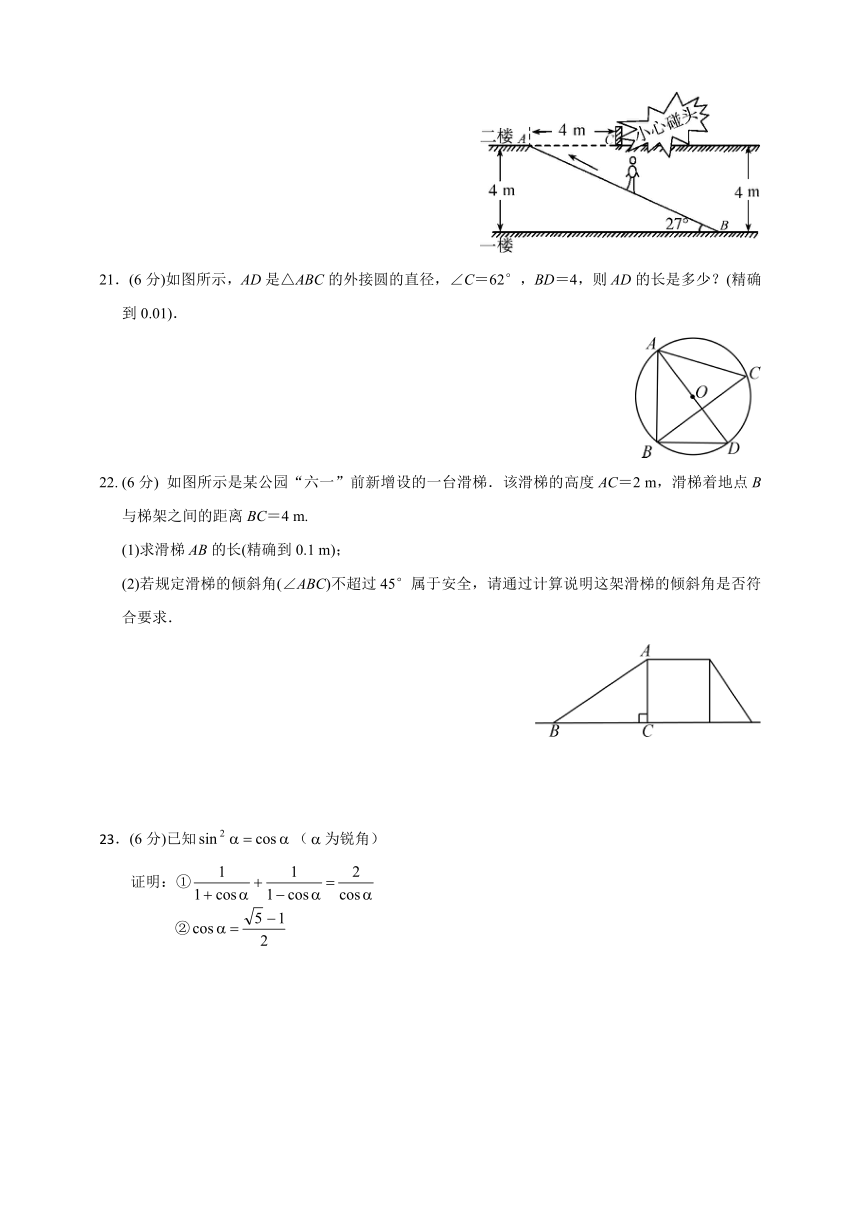
20.(6分) 4.如图所示,某超市在一楼至二楼之间安有电梯,天花板与地面平行,请你根据图中数据计算回答:小敏身高1.78 m,她乘电梯会有碰头的危险吗?姚明身高2.26 m,他乘电梯会有碰头的危险吗?(可能用到的三角函数值利用计算器完成)
21.(6分)如图所示,AD是△ABC的外接圆的直径,∠C=62°,BD=4,则AD的长是多少?(精确到0.01).
22. (6分) 如图所示是某公园“六一”前新增设的一台滑梯.该滑梯的高度AC=2 m,滑梯着地点B与梯架之间的距离BC=4 m.
(1)求滑梯AB的长(精确到0.1 m);
(2)若规定滑梯的倾斜角(∠ABC)不超过45°属于安全,请通过计算说明这架滑梯的倾斜角是否符合要求.
23.(6分)已知(为锐角)
证明:①
②
24. (8分) 已知中,∠BDC=30°,求15°和75°的四个三角函数值。
25. (8分) 数学老师布置了这样一个问题:如果α,β都为锐角,且tanα=,tanβ=.求α+β的度数.甲、乙两位同学想利用正方形网格构图来解决问题.他们分别设计了图1和图2.
(1)请你分别利用图1,图2求出α+β的度数,并说明理由;
(2)请参考以上思考问题的方法,选择一种方法解决下面问题:
如果α,β都为锐角,当tanα=5,tanβ=时,在图3的正方形网格中,利用已作出的锐角α,画出∠MON,使得∠MON=α-β.求出α-β的度数,并说明理由.
参考答案
1-5 AACAD
6-10 CCBDC
11. ;
12. 31°47′56″
13. 120
14. 1,
15. 22°9′12″
16. 30°
17.
18. 1
19. 解:(1)2cos60°+3tan30°
=1+
(2)sin260°+tan60°·cos30°
(3)sin30°+cos260°- tan30°
20. 【解析】计算C点到电梯的高度,再分别与两人的身高相比较.
解: 因为AC平行地面,所以∠CAB=27°,电梯到C点的高度=AC·tan27°≈4×0.51=2.04(m),1.78<2.04<2.26,故小敏没有碰头的危险,而姚明有碰头的危险..
21. 解: 由题意知∠D=∠C=62°,∵AD为直径,
∴∠ABD=90°.
在Rt△ABD中,cos ∠ADB=,
∴AD=≈8.52.
22. 解:(1)滑梯长AB==≈4.5(m).
(2)∵tan ∠ABC==,
∴∠ABC≈27°,27°<45°,
∴这架滑梯的倾斜角符合要求.
23. 解析:应充分利用同角三角函数的关系式。
证明:①左式通分得 又由知
命题得证。
②在已知中等量代换,使成为一个关于的方程。
但为锐角,
24. 解:如图,延长CD到点A,使AD=BD,设BC=1。
则,
25. 解:(1)①如图1中,只要证明△AMC≌△CNB,即可证明△ACB是等腰直角三角形,∠BAC=α+β=45°.②如图2中,只要证明△CEB∽△BEA,即可证明∠BED=α+β=45°. (2)如图3中,∠MOE=α,∠NOH=β,∠MON=α-β,只要证明△MFN≌△NHO即可解决问题.∠MON=α-β=45°.
1.2 锐角三角函数的计算
题号
一
二
三
总分
得分
第Ⅰ卷(选择题)
评卷人
得 分
一.选择题(共10小题,3*10=30)
1.用计算器求cos 15°,正确的按键顺序是 ( )
A.
B.
C.
D.
2. Rt△ABC中,∠C=90°,tan A=,则sin B的值为 ( )
A. B. C. D.
3. 已知sinα·sin45°=,则锐角α为( )
A.30° B.60° C. 45° D.75°
4.若tan(α+10°)=1,则锐角α的度数是 ( )
A.20° B.30° C.40° D.50°
5.将一副三角尺按如图放置,则上下两块三角尺的面积比S1:S2是( ).
A.2:3 B.2:(-1) C.:2 D.2:
6.若∠A是锐角,且cosA=tan30°,则( )
A.0°<∠A<30° B.30°<∠A<45°
C.45°<∠A<60° D.60°<∠A<90°
7.如图,在矩形ABCD中,若AD=1,AB=,则该矩形的两条对角线所成的锐角是( )
A.30° B.45° C.60° D.75°
8.如图所示是一张简易活动餐桌,测得OA=OB=30cm,OC=OD=50cm,现要求桌面离地面的高度为40cm,那么两条桌脚的张角∠COD的度数大小应为( )
A.100° B.120° C.135° D.150°
9.在△ABC中,∠A,∠B都是锐角,且sinA=,cosB=,则△ABC三个角的大小关系是( )
A.∠C>∠A>∠B B.∠B<∠C<∠A
C.∠A>∠B>∠C D.∠C>∠B>∠A
10.若θ为三角形的一个锐角,且2sinθ-=0,则θ等于( )
A.30° B.45° C.60° D.75°
第Ⅱ卷(非选择题)
评卷人
得 分
二.填空题(共8小题,3*8=24)
11.在Rt△ABC中,∠C=90°,若AC=3,AB=5,则sinA=______,tanB=______
12. 已知一个小山坡的坡度为0.62,则它的坡角为______(用计算器计算,精确到1″).
13.等腰三角形的底边长为20cm,面积为cm2,则顶角为________度.
14.化简_________,______。
15.要加工形状如图的零件,根据图示尺寸(单位:mm)计算斜角α的度数为____________.(用计算器计算,精确到1″).
16.关于x的一元二次方程x2-x+sinα=0有两个相等的实数根,则锐角α=______.
17.如图,在Rt△ABC中,∠ACB=90°,点D是AB的中点,tan∠BCD=3,则sinA=______.
18. =______
评卷人
得 分
三.解答题(共7小题, 46分)
19.(6分) 计算:
(1)2cos60°+3tan30°
(2)sin260°+tan60·cos30°
(3)sin30°+cos260°- tan30°
20.(6分) 4.如图所示,某超市在一楼至二楼之间安有电梯,天花板与地面平行,请你根据图中数据计算回答:小敏身高1.78 m,她乘电梯会有碰头的危险吗?姚明身高2.26 m,他乘电梯会有碰头的危险吗?(可能用到的三角函数值利用计算器完成)
21.(6分)如图所示,AD是△ABC的外接圆的直径,∠C=62°,BD=4,则AD的长是多少?(精确到0.01).
22. (6分) 如图所示是某公园“六一”前新增设的一台滑梯.该滑梯的高度AC=2 m,滑梯着地点B与梯架之间的距离BC=4 m.
(1)求滑梯AB的长(精确到0.1 m);
(2)若规定滑梯的倾斜角(∠ABC)不超过45°属于安全,请通过计算说明这架滑梯的倾斜角是否符合要求.
23.(6分)已知(为锐角)
证明:①
②
24. (8分) 已知中,∠BDC=30°,求15°和75°的四个三角函数值。
25. (8分) 数学老师布置了这样一个问题:如果α,β都为锐角,且tanα=,tanβ=.求α+β的度数.甲、乙两位同学想利用正方形网格构图来解决问题.他们分别设计了图1和图2.
(1)请你分别利用图1,图2求出α+β的度数,并说明理由;
(2)请参考以上思考问题的方法,选择一种方法解决下面问题:
如果α,β都为锐角,当tanα=5,tanβ=时,在图3的正方形网格中,利用已作出的锐角α,画出∠MON,使得∠MON=α-β.求出α-β的度数,并说明理由.
参考答案
1-5 AACAD
6-10 CCBDC
11. ;
12. 31°47′56″
13. 120
14. 1,
15. 22°9′12″
16. 30°
17.
18. 1
19. 解:(1)2cos60°+3tan30°
=1+
(2)sin260°+tan60°·cos30°
(3)sin30°+cos260°- tan30°
20. 【解析】计算C点到电梯的高度,再分别与两人的身高相比较.
解: 因为AC平行地面,所以∠CAB=27°,电梯到C点的高度=AC·tan27°≈4×0.51=2.04(m),1.78<2.04<2.26,故小敏没有碰头的危险,而姚明有碰头的危险..
21. 解: 由题意知∠D=∠C=62°,∵AD为直径,
∴∠ABD=90°.
在Rt△ABD中,cos ∠ADB=,
∴AD=≈8.52.
22. 解:(1)滑梯长AB==≈4.5(m).
(2)∵tan ∠ABC==,
∴∠ABC≈27°,27°<45°,
∴这架滑梯的倾斜角符合要求.
23. 解析:应充分利用同角三角函数的关系式。
证明:①左式通分得 又由知
命题得证。
②在已知中等量代换,使成为一个关于的方程。
但为锐角,
24. 解:如图,延长CD到点A,使AD=BD,设BC=1。
则,
25. 解:(1)①如图1中,只要证明△AMC≌△CNB,即可证明△ACB是等腰直角三角形,∠BAC=α+β=45°.②如图2中,只要证明△CEB∽△BEA,即可证明∠BED=α+β=45°. (2)如图3中,∠MOE=α,∠NOH=β,∠MON=α-β,只要证明△MFN≌△NHO即可解决问题.∠MON=α-β=45°.
