3.4 圆锥的侧面积与全面积 同步练习(含答案)
文档属性
| 名称 | 3.4 圆锥的侧面积与全面积 同步练习(含答案) | 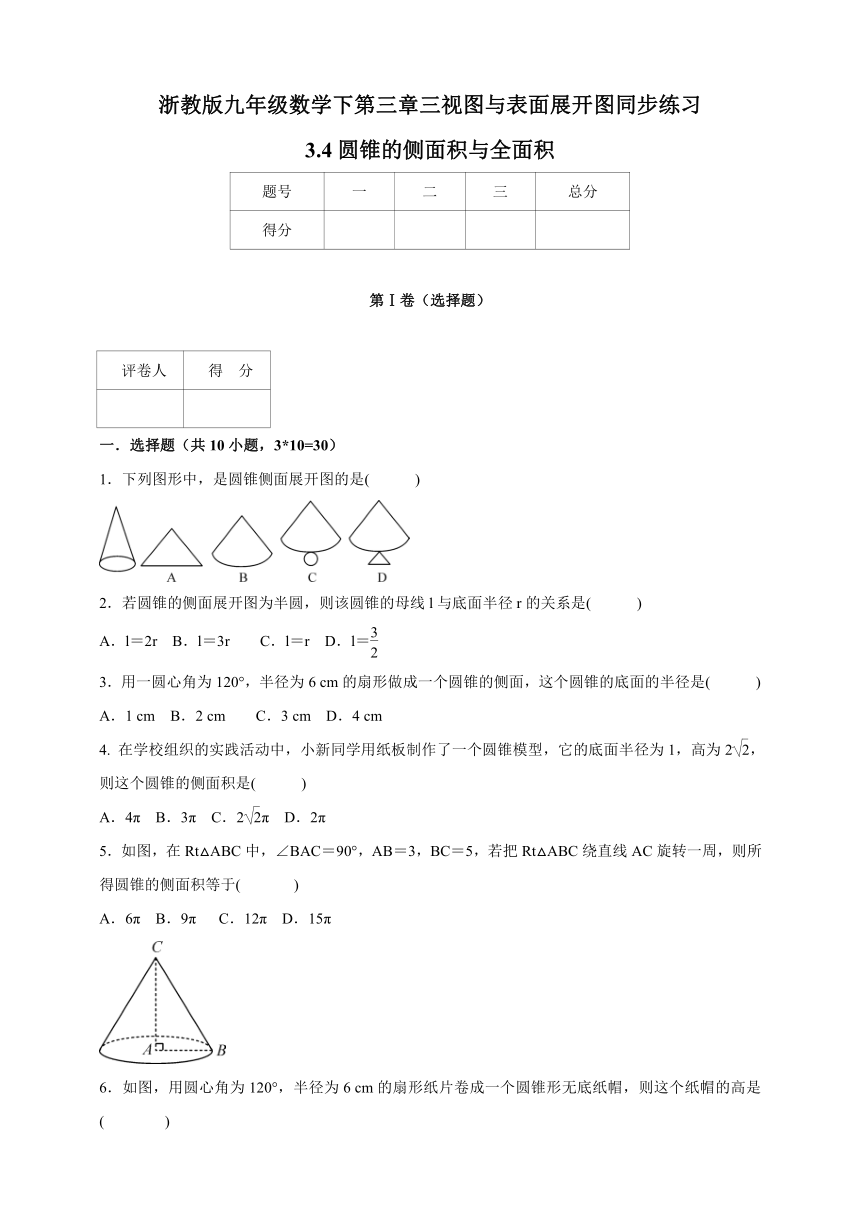 | |
| 格式 | zip | ||
| 文件大小 | 474.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-15 17:44:13 | ||
图片预览



文档简介
浙教版九年级数学下第三章三视图与表面展开图同步练习
3.4圆锥的侧面积与全面积
题号
一
二
三
总分
得分
第Ⅰ卷(选择题)
评卷人
得 分
一.选择题(共10小题,3*10=30)
1.下列图形中,是圆锥侧面展开图的是( )
2.若圆锥的侧面展开图为半圆,则该圆锥的母线l与底面半径r的关系是( )
A.l=2r B.l=3r C.l=r D.l=
3.用一圆心角为120°,半径为6 cm的扇形做成一个圆锥的侧面,这个圆锥的底面的半径是( )
A.1 cm B.2 cm C.3 cm D.4 cm
4. 在学校组织的实践活动中,小新同学用纸板制作了一个圆锥模型,它的底面半径为1,高为2,则这个圆锥的侧面积是( )
A.4π B.3π C.2π D.2π
5.如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于( )
A.6π B.9π C.12π D.15π
6.如图,用圆心角为120°,半径为6 cm的扇形纸片卷成一个圆锥形无底纸帽,则这个纸帽的高是( )
A. cm B.3 cm C.4 cm D.4 cm
7.将一个圆心角是90°的扇形围成圆锥的侧面,则该圆锥的侧面积S侧和底面积S底的关系为( )
A.S侧=S底 B.S侧=2S底 C.S侧=3S底 D.S侧=4S底
8.如图,扇形OED的半径为3,边长为的菱形OABC的顶点A,C,B分别在OD,OE,上,若把扇形OED围成一个圆锥,则此圆锥的高为( )
A. B.2 C. D.
9.已知圆锥的底面半径为3 cm,母线长为6 cm,则圆锥的侧面积是( )
A.20 cm2 B.20 π cm2 C.18 π cm2 D.18 cm2
10.若一个圆锥的侧面积是10,圆锥母线l与底面半径r之间的函数关系图象大致是( )
第Ⅱ卷(非选择题)
评卷人
得 分
二.填空题(共8小题,3*8=24)
11. 已知圆锥的母线是3 cm,底面半径是1 cm,则圆锥的表面积是_________cm2.
12.若一个圆锥的主视图是腰长为5,底边长为6的等腰三角形,则该圆锥的侧面积是___________.
13.已知圆锥的底面半径为40 cm,母线长为90 cm,则它的侧面展开图的圆心角为________度.
14.如图,如果从半径为5 cm的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高是______cm.
15.小刚用一张半径为24 cm的扇形纸板做一个圆锥形小丑帽子侧面(接缝面积忽略不计),如果做成的圆锥形小丑帽子的底面半径为10 cm,那么这张扇形纸板的面积是__________cm2.
16. 已知一个扇形的半径为60厘米,圆心角为150°.用它围成一个圆锥的侧面,那么圆锥的底面半径为_______厘米.
17. 如图,有一直径为 m的圆形纸片,要从中去一个最大的圆心角是90°的扇形ABC.
则被剪掉的阴影部分的面积是_______________
18.如图,在⊙O中,AB=4,AC是⊙O的直径,AC⊥BD于点F,∠A=30°.若用阴影扇形OBD围成一个圆锥侧面,则这个圆锥的底面圆的半径是____________.
评卷人
得 分
三.解答题(共6小题, 46分)
19.(6分) 如图,在半径为50 cm的圆形铁片上剪一块扇形铁片,用它制作成一个底面直径为80 cm,母线长为50 cm的圆锥形烟囱帽,求剪下来的扇形的圆心角的度数.
20.(6分)如图所示,圆锥底面圆的直径为6 cm,高为4 cm,则它的全面积为__________cm2.
21. (6分) 要在如图①所示的一个机器零件(尺寸如图②所示,单位:mm)的表面涂上防锈漆,请你帮助计算一下这个零件的表面积.(参考公式:S圆柱侧=2πrh,S圆锥侧=πrl,S圆=πr2,其中r为底面圆半径,h为高,l为母线长,π取3.14)
22.(6分) 圆锥形烟囱帽的底面直径是100 cm,母线长为60 cm,求它的侧面展开图中扇形的圆心角及面积.
23. (10分)现有一个圆心角为90°,半径为8 cm的扇形纸片,用它恰好可以围成一个圆锥的侧面(接缝忽略不计),求该圆锥底面圆的半径和该圆锥的全面积.
24.(12分) 如图,有一圆锥形粮堆,其轴截面示意图是边长为6 m的正△ABC,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路径是多少?
参考答案
1-5 BABBD
6-10 CDDCD
11. 4π
12. 15π
13. 160
14. 3
15. 240π
16. 25
17. π m2
18.
19. 解:母线l=50,底面半径r=40,∴圆心角度数θ=·360°=288°
20. 解:由条件知AO=4 cm,BC=6 cm,∴BO=3 cm.,Rt△AOB中,AB==5(cm),
运用圆锥的全面积公式得:S全=π×3×5+π×32=24π(cm2).
21. 解:S=S圆柱侧+S圆锥侧+S圆=2πrh+πrl+πr2==2π·40·100+π·40·50+π·1600=36424 mm2
22. 解:设其展开图中扇形的半径为R,弧长为l,圆心角为α,则R=60 cm,l=100π cm.由弧长公式l=,得n==300,即α=n°=300°,S扇形=×60×100π=3000π(cm2)
23. 解:由题意设围成的圆锥底面圆的半径为r cm,则2πr=·π·8,∴r=2,即该圆锥底面圆的半径为2 cm,则S全=S侧+S底=π·82+π522=20π(cm2),即该圆锥的全面积为20 πcm2
24. 解:设圆锥的底面半径为r,母线长为l,展开后所得扇形的圆心角的度数为n°,则底面圆的周长为2πr,侧面展开图的弧长为,∴2πr=.由题意知,轴截面△ABC为等边三角形,∵AB=BC,即l=2r=6.∴r=3,∴2π×3=,∴n=180,即其侧面展开图为半圆,如图,则△ABP为直角三角形,BP为最短线路.在Rt△ABP中,BP===3(m),即小猫所经过的最短路程是3m
3.4圆锥的侧面积与全面积
题号
一
二
三
总分
得分
第Ⅰ卷(选择题)
评卷人
得 分
一.选择题(共10小题,3*10=30)
1.下列图形中,是圆锥侧面展开图的是( )
2.若圆锥的侧面展开图为半圆,则该圆锥的母线l与底面半径r的关系是( )
A.l=2r B.l=3r C.l=r D.l=
3.用一圆心角为120°,半径为6 cm的扇形做成一个圆锥的侧面,这个圆锥的底面的半径是( )
A.1 cm B.2 cm C.3 cm D.4 cm
4. 在学校组织的实践活动中,小新同学用纸板制作了一个圆锥模型,它的底面半径为1,高为2,则这个圆锥的侧面积是( )
A.4π B.3π C.2π D.2π
5.如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于( )
A.6π B.9π C.12π D.15π
6.如图,用圆心角为120°,半径为6 cm的扇形纸片卷成一个圆锥形无底纸帽,则这个纸帽的高是( )
A. cm B.3 cm C.4 cm D.4 cm
7.将一个圆心角是90°的扇形围成圆锥的侧面,则该圆锥的侧面积S侧和底面积S底的关系为( )
A.S侧=S底 B.S侧=2S底 C.S侧=3S底 D.S侧=4S底
8.如图,扇形OED的半径为3,边长为的菱形OABC的顶点A,C,B分别在OD,OE,上,若把扇形OED围成一个圆锥,则此圆锥的高为( )
A. B.2 C. D.
9.已知圆锥的底面半径为3 cm,母线长为6 cm,则圆锥的侧面积是( )
A.20 cm2 B.20 π cm2 C.18 π cm2 D.18 cm2
10.若一个圆锥的侧面积是10,圆锥母线l与底面半径r之间的函数关系图象大致是( )
第Ⅱ卷(非选择题)
评卷人
得 分
二.填空题(共8小题,3*8=24)
11. 已知圆锥的母线是3 cm,底面半径是1 cm,则圆锥的表面积是_________cm2.
12.若一个圆锥的主视图是腰长为5,底边长为6的等腰三角形,则该圆锥的侧面积是___________.
13.已知圆锥的底面半径为40 cm,母线长为90 cm,则它的侧面展开图的圆心角为________度.
14.如图,如果从半径为5 cm的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高是______cm.
15.小刚用一张半径为24 cm的扇形纸板做一个圆锥形小丑帽子侧面(接缝面积忽略不计),如果做成的圆锥形小丑帽子的底面半径为10 cm,那么这张扇形纸板的面积是__________cm2.
16. 已知一个扇形的半径为60厘米,圆心角为150°.用它围成一个圆锥的侧面,那么圆锥的底面半径为_______厘米.
17. 如图,有一直径为 m的圆形纸片,要从中去一个最大的圆心角是90°的扇形ABC.
则被剪掉的阴影部分的面积是_______________
18.如图,在⊙O中,AB=4,AC是⊙O的直径,AC⊥BD于点F,∠A=30°.若用阴影扇形OBD围成一个圆锥侧面,则这个圆锥的底面圆的半径是____________.
评卷人
得 分
三.解答题(共6小题, 46分)
19.(6分) 如图,在半径为50 cm的圆形铁片上剪一块扇形铁片,用它制作成一个底面直径为80 cm,母线长为50 cm的圆锥形烟囱帽,求剪下来的扇形的圆心角的度数.
20.(6分)如图所示,圆锥底面圆的直径为6 cm,高为4 cm,则它的全面积为__________cm2.
21. (6分) 要在如图①所示的一个机器零件(尺寸如图②所示,单位:mm)的表面涂上防锈漆,请你帮助计算一下这个零件的表面积.(参考公式:S圆柱侧=2πrh,S圆锥侧=πrl,S圆=πr2,其中r为底面圆半径,h为高,l为母线长,π取3.14)
22.(6分) 圆锥形烟囱帽的底面直径是100 cm,母线长为60 cm,求它的侧面展开图中扇形的圆心角及面积.
23. (10分)现有一个圆心角为90°,半径为8 cm的扇形纸片,用它恰好可以围成一个圆锥的侧面(接缝忽略不计),求该圆锥底面圆的半径和该圆锥的全面积.
24.(12分) 如图,有一圆锥形粮堆,其轴截面示意图是边长为6 m的正△ABC,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路径是多少?
参考答案
1-5 BABBD
6-10 CDDCD
11. 4π
12. 15π
13. 160
14. 3
15. 240π
16. 25
17. π m2
18.
19. 解:母线l=50,底面半径r=40,∴圆心角度数θ=·360°=288°
20. 解:由条件知AO=4 cm,BC=6 cm,∴BO=3 cm.,Rt△AOB中,AB==5(cm),
运用圆锥的全面积公式得:S全=π×3×5+π×32=24π(cm2).
21. 解:S=S圆柱侧+S圆锥侧+S圆=2πrh+πrl+πr2==2π·40·100+π·40·50+π·1600=36424 mm2
22. 解:设其展开图中扇形的半径为R,弧长为l,圆心角为α,则R=60 cm,l=100π cm.由弧长公式l=,得n==300,即α=n°=300°,S扇形=×60×100π=3000π(cm2)
23. 解:由题意设围成的圆锥底面圆的半径为r cm,则2πr=·π·8,∴r=2,即该圆锥底面圆的半径为2 cm,则S全=S侧+S底=π·82+π522=20π(cm2),即该圆锥的全面积为20 πcm2
24. 解:设圆锥的底面半径为r,母线长为l,展开后所得扇形的圆心角的度数为n°,则底面圆的周长为2πr,侧面展开图的弧长为,∴2πr=.由题意知,轴截面△ABC为等边三角形,∵AB=BC,即l=2r=6.∴r=3,∴2π×3=,∴n=180,即其侧面展开图为半圆,如图,则△ABP为直角三角形,BP为最短线路.在Rt△ABP中,BP===3(m),即小猫所经过的最短路程是3m
