2.3 三角形的内切圆 同步练习(含答案)
文档属性
| 名称 | 2.3 三角形的内切圆 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 354.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-16 11:46:09 | ||
图片预览



文档简介
浙教版九年级数学下第二章直线与圆的位置关系同步练习
2.2 切线长定理
题号
一
二
三
总分
得分
第Ⅰ卷(选择题)
评卷人
得 分
一、选择题(共10小题,3*10=30)
1.下列说法中,不正确的是 ( )
A.三角形的内心是三角形三条内角平分线的交点
B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部
C.垂直于半径的直线是圆的切线
D.三角形的内心到三角形的三边的距离相等
2. 给出下列命题:①任一个三角形一定有一个外接圆,并且只有一个外接圆;②任一个圆一定有一个内接三角形,并且只有一个内接三角形;③任一个三角形一定有一个内切圆,并且只有一个内切圆;④任一个圆一定有一个外切三角形,并且只有一个外切三角形.其中真命题共有( )
A.1个 B.2个 C.3个 D.4个
3.已知如图所示,等边△ABC的边长为2cm,下列以A为圆心的各圆中, 半径是3cm的圆是( )
4.如图所示,⊙O的外切梯形ABCD中,如果AD∥BC,那么∠DOC的度数为( )
A.70° B.90° C.60° D.45°
5.△ABC的三边长分别为a、b、c,它的内切圆的半径为r,则△ABC的面积为( )
A.(a+b+c)r B.2(a+b+c) C.(a+b+c)r D.(a+b+c)r
6. 如图,在△ABC中,∠C=90°,AC=8,AB=10,点P在AC上,AP=2,若⊙O的圆心在线段BP上,且⊙O与AB、AC都相切,则⊙O的半径是( )
A. 1 B. C. D.
7. 正三角形内切圆半径r与外接圆半径R之间的关系为( )
A.4R=5r B.3R=4r C.2R=3r D.R=2r
8. 若正方形的边长为a,其内切圆的半径为r,外接圆的半径为R,则r∶R∶a=…( )
A. B. C. D.
9. 如图,内切于,切点分别为.已知,,连结,那么等于( )
A. B. C. D.
10. 若O是△ABC的内心,且∠BOC=100°,则∠A=( )
A.20° B.30° C.50° D.60°
第Ⅱ卷(非选择题)
评卷人
得 分
二.填空题(共8小题,3*8=24)
11.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,则∠A的度为________。
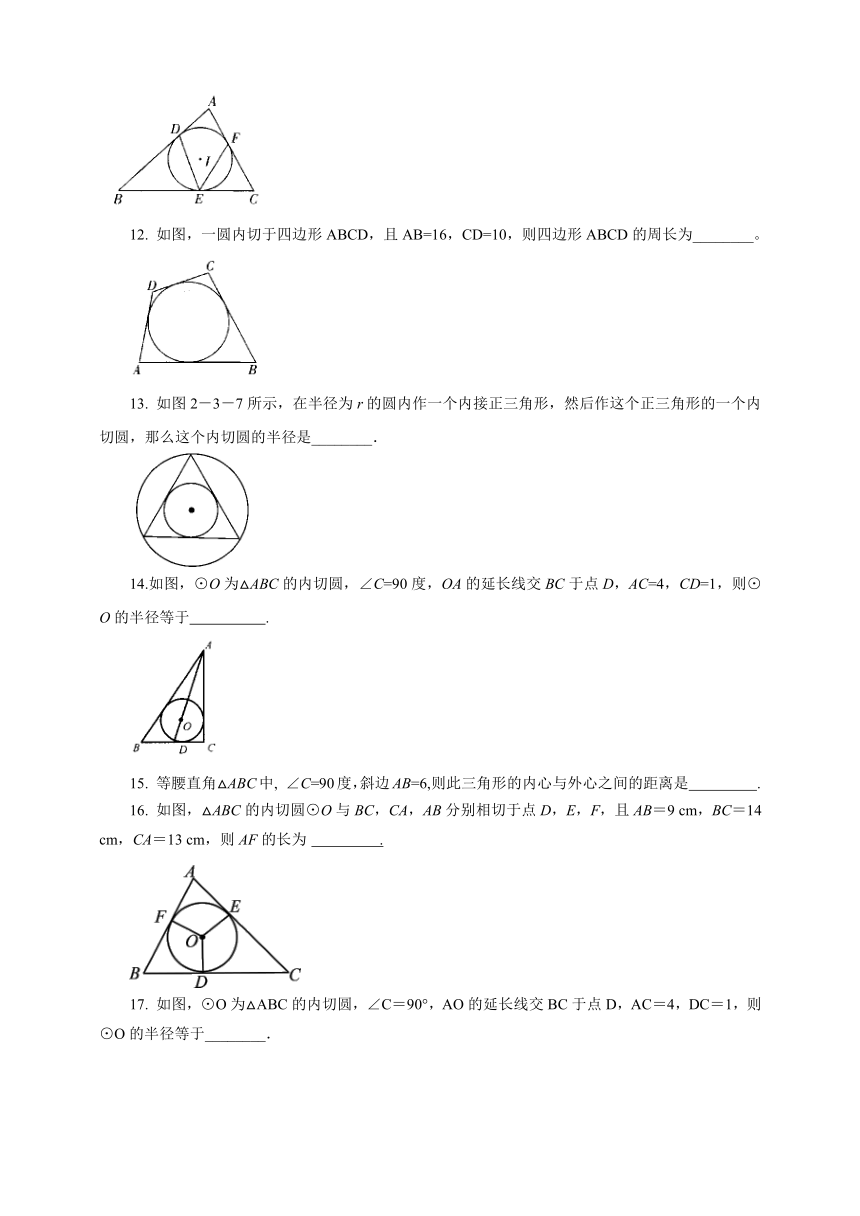
12. 如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________。
13. 如图2-3-7所示,在半径为r的圆内作一个内接正三角形,然后作这个正三角形的一个内切圆,那么这个内切圆的半径是________.
14.如图,⊙O为△ABC的内切圆,∠C=90度,OA的延长线交BC于点D,AC=4,CD=1,则⊙O的半径等于 .
15. 等腰直角△ABC中, ∠C=90度,斜边AB=6,则此三角形的内心与外心之间的距离是 .
16. 如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9 cm,BC=14 cm,CA=13 cm,则AF的长为 .
17. 如图,⊙O为△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,AC=4,DC=1,则⊙O的半径等于________.
18. 将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1,B1C1交CD于点E,AB=,则四边形AB1ED的内切圆半径为_________
评卷人
得 分
三.解答题(共7小题, 46分)
19.如图,点I是△ABC的内心,线段AI的延长线交△ ABC的外接圆于点D,交BC边于点E.求证:ID=BD.
20. 如图,园林部门准备在公园的三条小道围成的地域内建造一个圆形喷水池,要求它的面积尽量大,请设计水池的半径与圆心.
21. (6分) 如图, △ABC中, AB=10, BC=8, AC=7, ⊙O为△ABC的内切圆, 切点分别是D, E, F. 求AD的长.
22. 如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC的外接圆于点E.
(1)求证:IE=BE;
(2)若IE=4,AE=8,求DE的长.
23. (6分) 如图,△ABC外切于⊙O,切点分别为点D,E,F,∠A=60°,BC=7,⊙O的半径为.求:
24.(8分) 已知:如图5,PA、PB是⊙O的切线;A、B是切点;连结OA、OB、OP.
①若∠COP=∠DOP,求证:AC=BD;
②连结CD,设△PCD的周长为l,若l=2AP,判断直线CD与⊙O的位置关系,并说明理由.
25. (8分) 如图2-3-8,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D,E,F.
(1)求证:BE=CE;
(2)若∠A=90°,AB=AC=2,求⊙O的半径.
参考答案
1-5 CBCBA
6-10 ADDBA
11. 76°
12. 52
13.
14.
15. 6
16. 4 cm
17.
18.
19. 解:∵ 点I是△ABC的内心,∴ ∠BAD=∠CAD,∠ABI=∠CBI.
∵ ∠CBD=∠CAD,∴ ∠BAD=∠CBD.
∴ ∠BID=∠ABI+∠BAD =∠CBI+∠CBD=∠IBD. ∴ID=BD.
20. 解:作∠ABC和∠BCA的平分线BM,CN,其交点为圆心,因为402+92=412,所以△ABC为直角三角形,由面积法(AB+BC+AC)×半径=×40×9,则半径为4m
21. 解:连结OD, OF, OA.
∵AB, AC是⊙O的切线, ∴∠ODA=∠OFA=90°.
又∵OD=OF, OA=OA, ∴Rt△OAD≌Rt△OAF, ∴AD=AF.
同理, BD=BE, CE=CF.
∵BE+CE=BC=8, ∴BD+BE+CE+CF=16. ∴2AD=(10+8+7)-16=9, 即AD=4.5.
22. 解: 连结IB.∵点I是△ABC的内心,∴∠BAD=∠CAD,∠ABI=∠IBD.又∵∠BIE=∠BAD+∠ABI,∴∠BIE=∠CAD+∠IBD=∠DBE+∠IBD=∠IBE,∴BE=IE;
(2)在△BED和△AEB中,∵∠EBD=∠CAD=∠EAB,∠BED=∠AEB,∴△BED∽△AEB,∴=.∵IE=4,∴BE=4.∵AE=8,∴DE==2.
23. 解:(1)∵△ABC外切于⊙O,切点分别为点D、E、F,∴BF=BD,CE=CD,∴BF+CE=BD+CD=BC=7,所以BF+CE的值是7.
连结OE、OA.∵△ABC外切于⊙O,切点分别为点D、E、F,∴AE=AF,∠OEA=90°,∠OAE=∠BAC=30°,∴OA=2OE=2.由勾股定理得AE=AF===3,∴AB+BC+AC=AF+AE+CE+BF+BC=7+7+3+3=20,∴△ABC的周长是20.
24. 解:(1)∵PA、PB是⊙O的切线,∴∠OAP=90°. ∵∠AOP=60°,∴∠OPA=30°=∠OPB.
(2) ①∵∠COP=∠DOP,∠CPO=∠DPO,PO=PO, ∴△OCP≌△ODP,∴CP=DP.
又可证△OPA≌OPB得PA=PB, ∴AC=BD.
②作OE⊥CD于E,设OE=d,CE=x,DE=y. 则d2=AC2+AO2-x2=BD2+OA2-y2.
∴(AC+x)(AC-x)- (BD+y)(BD-y)=0, ∵l=2AP=2BP,∴x+y=AC+BD, ∴AC-x=y-BD.
∴(AC+x)(y-BD)- (BD+y)(BD-y)=0, ∴(y-BD) (AC+x+BD+y)=0.
∵AC+x+BD+y≠0,∴y=BD, 即d=AO,∴直线CD与⊙O相切.
25. 解:(1)证明:∵⊙O是△ABC的内切圆,切点为D,E,F,
∴AD=AF,BD=BE,CE=CF,
∵AB=AC,
∴AB-AD=AC-AF,
即BD=CF,∴BE=CE.
(2) 连结OD,OF.
∵⊙O是△ABC的内切圆,切点为D,E,F,
∴∠ODA=∠OFA=∠A=90°,
又∵OD=OF,
∴四边形ODAF是正方形,
设OD=AD=AF=r,
则BE=BD=CF=CE=2-r.
在△ABC中,∠A=90°,
∴BC==2,
又∵BC=BE+CE,∴(2-r)+(2-r)=2,
得r=2-,∴⊙O的半径是2-.
2.2 切线长定理
题号
一
二
三
总分
得分
第Ⅰ卷(选择题)
评卷人
得 分
一、选择题(共10小题,3*10=30)
1.下列说法中,不正确的是 ( )
A.三角形的内心是三角形三条内角平分线的交点
B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部
C.垂直于半径的直线是圆的切线
D.三角形的内心到三角形的三边的距离相等
2. 给出下列命题:①任一个三角形一定有一个外接圆,并且只有一个外接圆;②任一个圆一定有一个内接三角形,并且只有一个内接三角形;③任一个三角形一定有一个内切圆,并且只有一个内切圆;④任一个圆一定有一个外切三角形,并且只有一个外切三角形.其中真命题共有( )
A.1个 B.2个 C.3个 D.4个
3.已知如图所示,等边△ABC的边长为2cm,下列以A为圆心的各圆中, 半径是3cm的圆是( )
4.如图所示,⊙O的外切梯形ABCD中,如果AD∥BC,那么∠DOC的度数为( )
A.70° B.90° C.60° D.45°
5.△ABC的三边长分别为a、b、c,它的内切圆的半径为r,则△ABC的面积为( )
A.(a+b+c)r B.2(a+b+c) C.(a+b+c)r D.(a+b+c)r
6. 如图,在△ABC中,∠C=90°,AC=8,AB=10,点P在AC上,AP=2,若⊙O的圆心在线段BP上,且⊙O与AB、AC都相切,则⊙O的半径是( )
A. 1 B. C. D.
7. 正三角形内切圆半径r与外接圆半径R之间的关系为( )
A.4R=5r B.3R=4r C.2R=3r D.R=2r
8. 若正方形的边长为a,其内切圆的半径为r,外接圆的半径为R,则r∶R∶a=…( )
A. B. C. D.
9. 如图,内切于,切点分别为.已知,,连结,那么等于( )
A. B. C. D.
10. 若O是△ABC的内心,且∠BOC=100°,则∠A=( )
A.20° B.30° C.50° D.60°
第Ⅱ卷(非选择题)
评卷人
得 分
二.填空题(共8小题,3*8=24)
11.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,则∠A的度为________。
12. 如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________。
13. 如图2-3-7所示,在半径为r的圆内作一个内接正三角形,然后作这个正三角形的一个内切圆,那么这个内切圆的半径是________.
14.如图,⊙O为△ABC的内切圆,∠C=90度,OA的延长线交BC于点D,AC=4,CD=1,则⊙O的半径等于 .
15. 等腰直角△ABC中, ∠C=90度,斜边AB=6,则此三角形的内心与外心之间的距离是 .
16. 如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9 cm,BC=14 cm,CA=13 cm,则AF的长为 .
17. 如图,⊙O为△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,AC=4,DC=1,则⊙O的半径等于________.
18. 将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1,B1C1交CD于点E,AB=,则四边形AB1ED的内切圆半径为_________
评卷人
得 分
三.解答题(共7小题, 46分)
19.如图,点I是△ABC的内心,线段AI的延长线交△ ABC的外接圆于点D,交BC边于点E.求证:ID=BD.
20. 如图,园林部门准备在公园的三条小道围成的地域内建造一个圆形喷水池,要求它的面积尽量大,请设计水池的半径与圆心.
21. (6分) 如图, △ABC中, AB=10, BC=8, AC=7, ⊙O为△ABC的内切圆, 切点分别是D, E, F. 求AD的长.
22. 如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC的外接圆于点E.
(1)求证:IE=BE;
(2)若IE=4,AE=8,求DE的长.
23. (6分) 如图,△ABC外切于⊙O,切点分别为点D,E,F,∠A=60°,BC=7,⊙O的半径为.求:
24.(8分) 已知:如图5,PA、PB是⊙O的切线;A、B是切点;连结OA、OB、OP.
①若∠COP=∠DOP,求证:AC=BD;
②连结CD,设△PCD的周长为l,若l=2AP,判断直线CD与⊙O的位置关系,并说明理由.
25. (8分) 如图2-3-8,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D,E,F.
(1)求证:BE=CE;
(2)若∠A=90°,AB=AC=2,求⊙O的半径.
参考答案
1-5 CBCBA
6-10 ADDBA
11. 76°
12. 52
13.
14.
15. 6
16. 4 cm
17.
18.
19. 解:∵ 点I是△ABC的内心,∴ ∠BAD=∠CAD,∠ABI=∠CBI.
∵ ∠CBD=∠CAD,∴ ∠BAD=∠CBD.
∴ ∠BID=∠ABI+∠BAD =∠CBI+∠CBD=∠IBD. ∴ID=BD.
20. 解:作∠ABC和∠BCA的平分线BM,CN,其交点为圆心,因为402+92=412,所以△ABC为直角三角形,由面积法(AB+BC+AC)×半径=×40×9,则半径为4m
21. 解:连结OD, OF, OA.
∵AB, AC是⊙O的切线, ∴∠ODA=∠OFA=90°.
又∵OD=OF, OA=OA, ∴Rt△OAD≌Rt△OAF, ∴AD=AF.
同理, BD=BE, CE=CF.
∵BE+CE=BC=8, ∴BD+BE+CE+CF=16. ∴2AD=(10+8+7)-16=9, 即AD=4.5.
22. 解: 连结IB.∵点I是△ABC的内心,∴∠BAD=∠CAD,∠ABI=∠IBD.又∵∠BIE=∠BAD+∠ABI,∴∠BIE=∠CAD+∠IBD=∠DBE+∠IBD=∠IBE,∴BE=IE;
(2)在△BED和△AEB中,∵∠EBD=∠CAD=∠EAB,∠BED=∠AEB,∴△BED∽△AEB,∴=.∵IE=4,∴BE=4.∵AE=8,∴DE==2.
23. 解:(1)∵△ABC外切于⊙O,切点分别为点D、E、F,∴BF=BD,CE=CD,∴BF+CE=BD+CD=BC=7,所以BF+CE的值是7.
连结OE、OA.∵△ABC外切于⊙O,切点分别为点D、E、F,∴AE=AF,∠OEA=90°,∠OAE=∠BAC=30°,∴OA=2OE=2.由勾股定理得AE=AF===3,∴AB+BC+AC=AF+AE+CE+BF+BC=7+7+3+3=20,∴△ABC的周长是20.
24. 解:(1)∵PA、PB是⊙O的切线,∴∠OAP=90°. ∵∠AOP=60°,∴∠OPA=30°=∠OPB.
(2) ①∵∠COP=∠DOP,∠CPO=∠DPO,PO=PO, ∴△OCP≌△ODP,∴CP=DP.
又可证△OPA≌OPB得PA=PB, ∴AC=BD.
②作OE⊥CD于E,设OE=d,CE=x,DE=y. 则d2=AC2+AO2-x2=BD2+OA2-y2.
∴(AC+x)(AC-x)- (BD+y)(BD-y)=0, ∵l=2AP=2BP,∴x+y=AC+BD, ∴AC-x=y-BD.
∴(AC+x)(y-BD)- (BD+y)(BD-y)=0, ∴(y-BD) (AC+x+BD+y)=0.
∵AC+x+BD+y≠0,∴y=BD, 即d=AO,∴直线CD与⊙O相切.
25. 解:(1)证明:∵⊙O是△ABC的内切圆,切点为D,E,F,
∴AD=AF,BD=BE,CE=CF,
∵AB=AC,
∴AB-AD=AC-AF,
即BD=CF,∴BE=CE.
(2) 连结OD,OF.
∵⊙O是△ABC的内切圆,切点为D,E,F,
∴∠ODA=∠OFA=∠A=90°,
又∵OD=OF,
∴四边形ODAF是正方形,
设OD=AD=AF=r,
则BE=BD=CF=CE=2-r.
在△ABC中,∠A=90°,
∴BC==2,
又∵BC=BE+CE,∴(2-r)+(2-r)=2,
得r=2-,∴⊙O的半径是2-.
