第五章 特殊平行四边形解答题精选(1)(含解析)
文档属性
| 名称 | 第五章 特殊平行四边形解答题精选(1)(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-20 14:07:23 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
浙教新版八年级下学期《第5章 特殊平行四边形》解答题精选
解答题(共46小题)
1.已知:(x﹣2)2+(5﹣x)2=.若把x﹣2与5﹣x看成一个长方形的长和宽,求这个长方形的周长和面积.
2.如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.
(1)如图1,若点E为线段AM的中点,BM:CM=1:2,BE=,求AB的长;
(2)如图2.若G为AE中点,延长DG至N,使DG=NG,连接EN,且∠EDG=∠ENG.求证:BF+DF=AF.
3.已知菱形ABCD,E为AD上一点,且BA=BE,连接BD.
(1)如图1,过B作BF⊥AD,垂足为F,若BD=2,DE=1,求菱形ABCD的边长.
(2)如图2,点M为边CD上一点,连接BM,且∠CBM=∠DBE,过E作EG⊥BM,垂足为G点,O为BD中点,连接GO并延长交BE于H点,交AD于N点,求证AN=EN.
4.在四边形ABCD中,对角线AC、BD相交于点O,过点O的两条直线分别交边AB、CD、AD、BC于点E、F、G、H.
【感知】如图①,若四边形ABCD是正方形,且AG=BE=CH=DF,则S四边形AEOG= S正方形ABCD;
【拓展】如图②,若四边形ABCD是矩形,且S四边形AEOG=S矩形ABCD,设AB=a,AD=b,BE=m,求AG的长(用含a、b、m的代数式表示);
【探究】如图③,若四边形ABCD是平行四边形,且AB=3,AD=5,BE=1,试确定F、G、H的位置,使直线EF、GH把四边形ABCD的面积四等分.
5.如图,平行四边形ABCD,F是对角线AC上的一点,过点D作DE∥AC,且DE=CF,连接AE、DE、EF.
(1)求证:△ADE≌△BCF;
(2)若∠BAF+∠AED=180°,求证:四边形ABFE为菱形.
6.菱形ABCD中,∠ABC=60°,点E在AD上,连接BE,点F、H在BE上,△AFH为等边三角形.
(1)如图1,若CE⊥AD,BE=,求菱形ABCD的面积;
(2)如图2,点G在AC上,连接FG,HC,若FG∥AH,HC=2AH,求证:AG=GC.
7.已知:在平行四边形ABCD中,点O是边AD的中点,连接CO并延长交BA延长线于点E,连接ED、AC.
(1)如图1,求证:四边形AEDC是平行四边形;
(2)如图2,若四边形AEDC是矩形,请探究∠COD与∠B的数量关系,写出你的探究结论,并加以证明.
8.如图1,P为正方形ABCD内一点,且PA:PB:PC=1:2:3,求∠APB的度数.
小明同学的想法是:不妨设PA=x,PB=2x,PC=3x,设法把PA、PB、PC相对集中,于是他将△BCP绕点B顺时针旋转90°得到△BAE(如图2),然后连结PE,问题得以解决.请你回答图2中∠APB= 度.
请你参考小明同学的方法,解答下列问题.
如图3,P是等边△ABC内一点,PA:PB:PC=3:4:5,那么∠APB= 度.请写出推理过程.
9.(1)如图①,分别以△ABC的边AB、AC为一边向形外作正方形ABDE和正方形ACGF.求证S△AEF=S△ABC.
(2)如图②,分别以△ABC的边AB、AC、BC为边向形外作正方形ABDE、ACGF、BCHI,可得六边形DEFGHI,若S正方形ABDE=17,S正方形ACGF=25,S正方形BCHI=16,求S六边形DEFGHI.
10.如图1,点E为正方形ABCD的边AB上一点,EF⊥EC,且EF=EC,连接AF.
(1)求∠EAF的度数;
(2)如图2,连接FC交BD于M,交AD于N.求证:BD=AF+2DM.
11.如图(1),在Rt△ABC,∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连结AD、CF,AD与CF交于点M.
(1)求证:△ABD≌△FBC;
(2)如图(2),求证:AM2+MF2=AF2.
12.如图,DE是平行四边形ABCD中∠ADC的角平分线,EF∥AD交DC于F.
(1)如图1,求证:四边形AEFD是菱形;
(2)如图2,连接FB,FB⊥AB,若∠DAB=60°,FC=2,请直接写出所有长度为4的线段.
13.已知:分别以△ABC的各边为边,在BC边的同侧作等边三角形ABE、等边三角形CBD和等边三角形ACF,连结DE,DF.
(1)试说明四边形DEAF为平行四边形.
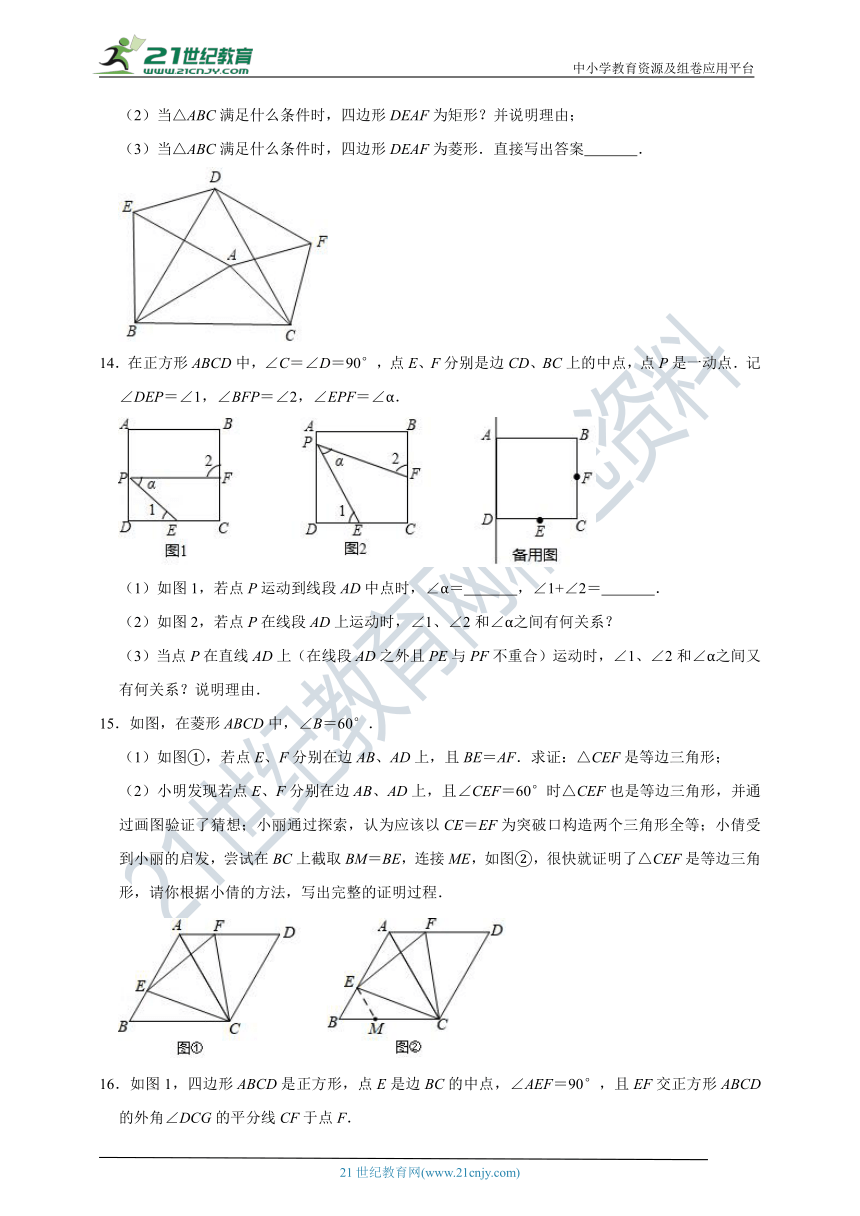
(2)当△ABC满足什么条件时,四边形DEAF为矩形?并说明理由;
(3)当△ABC满足什么条件时,四边形DEAF为菱形.直接写出答案 .
14.在正方形ABCD中,∠C=∠D=90°,点E、F分别是边CD、BC上的中点,点P是一动点.记∠DEP=∠1,∠BFP=∠2,∠EPF=∠α.
(1)如图1,若点P运动到线段AD中点时,∠α= ,∠1+∠2= .
(2)如图2,若点P在线段AD上运动时,∠1、∠2和∠α之间有何关系?
(3)当点P在直线AD上(在线段AD之外且PE与PF不重合)运动时,∠1、∠2和∠α之间又有何关系?说明理由.
15.如图,在菱形ABCD中,∠B=60°.
(1)如图①,若点E、F分别在边AB、AD上,且BE=AF.求证:△CEF是等边三角形;
(2)小明发现若点E、F分别在边AB、AD上,且∠CEF=60°时△CEF也是等边三角形,并通过画图验证了猜想;小丽通过探索,认为应该以CE=EF为突破口构造两个三角形全等;小倩受到小丽的启发,尝试在BC上截取BM=BE,连接ME,如图②,很快就证明了△CEF是等边三角形,请你根据小倩的方法,写出完整的证明过程.
16.如图1,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形ABCD的外角∠DCG的平分线CF于点F.
(1)如图2,取AB的中点H,连接HE,求证:AE=EF.
(2)如图3,若点E是BC的延长线上(除C点外)的任意一点,其他条件不变结论“AE=EF”仍然成立吗?如果正确,写出证明过程:如果不正确,请说明理由.
17.如图,四边形ABCD和四边形CEFG都是正方形,且BC=CD,CE=CG,∠BCD=∠GCE=90°.
(1)求证:△BCG≌△DCE;
(2)求证:BG⊥DE.
18.已知:在正方形ABCD和正方形DEFG中,顶点B、D、F在同一直线上,H是BF的中点.
(1)如图①,若AB=1,DG=2,求BH的长;
(2)如图②,连接AH、GH,求证:AH=GH且AH⊥GH.
19.如图,点P是正方形ABCD的对角线AC上的一点,PM⊥AB,PN⊥BC,垂足分别为点M,N,求证:DP=MN.
20.如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.
21.如图,四边形ABCD是正方形,AC与BD,相交于点O,点E、F是边AD上两动点,且AE=DF,BE与对角线AC交于点G,联结DG,DG交CF于点H.
(1)求证:∠ADG=∠DCF;
(2)联结HO,试证明HO平分∠CHG.
22.如图,已知AD是Rt△ABC斜边BC上的高,∠B的平分线交AD于M交AC于E,∠DAC的平分线交ME于O,交CD于N.求证:四边形AMNE是菱形.
23.如图,正方形ABCD的对角线AC,BD相交于点O,AB=3,E为OC上一点,OE=1,连接BE,过点A作AF⊥BE于点F,与BD交于点G.
(1)BE与AG相等吗?若相等,请证明,若不相等,请说明理由;
(2)求AF的长.
24.如图,正方形ABCD中,AB=4,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE、EF为邻边作矩形DEFG,连接AG.
(1)求证:矩形DEFG是正方形;
(2)求AG+AE的值;
(3)若F恰为AB中点,连接DF交AC于点M,请直接写出ME的长.
25.如图,在正方形ABCD的外侧,作等边三角形BCE,连接AE,DE.
(1)求证:AE=DE
(2)过点D作DF⊥AE,垂足为F,若AB=2cm,求DF的长.
26.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=CD,求证:∠AEF=90°.
27.如图①,正方形ABCD中,点E、F都在AD边上,且AE=FD,分别连接BE、FC,对角线BD交FC于点P,连接AP,交BE于点G;
(1)试判断AP与BE的位置关系;
(2)如图②,再过点P作PH⊥AP,交BC于点H,连接AH,分别交BE、BD于点N,M,请直接写出图②中有哪些等腰三角形.
28.如图,正方形ABCD中,点E是BC延长线上一点,连接DE,过点B作BF⊥DE于点F,连接FC.
(1)求证:∠FBC=∠CDF;
(2)作点C关于直线DE的对称点G,连接CG,FG,猜想线段DF,BF,CG之间的数量关系,并证明你的结论.
29.(1)如图,已知等边△ABC的边长为10,点E是AB上一点,过点E作ED⊥AC于点D,过点D作DF⊥BC于点F.
①若AE=7,求BF的长;
②连接EF,若EF⊥AB,求AE的长;
(2)已知正方形ABCD的边长为10,点E是边AB上一点,过点E作∠AEF=60°交边AD于点F,再过点F作∠DFG=60°交边CD于点G,继续过点G作∠CGH=60°交边BC于点H,连接EH,若∠BHE=60°,请直接写出AE的长.
30.如图,以△ABC的各边为边长,在边BC的同侧分别作正方形ABDI,正方形BCFE,正方形ACHG,连接AD,DE,EG.
(1)求证:△BDE≌△BAC;
(2)①设∠BAC=α,请用含α的代数式表示∠EDA,∠DAG;
②求证:四边形ADEG是平行四边形;
(3)当△ABC满足什么条件时,四边形ADEG是正方形?请说明理由.
31.在△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG,DF.
(1)求证:BD=DF;
(2)求证:四边形BDFG为菱形;
(3)若AG=5,CF=,求四边形BDFG的周长.
32.如图,长方形ABCD在平面直角坐标系中,已知点A(0,a),B(0,6),C(b,6),且满足a=+8.
(1)请直接写出A、C、D三个点的坐标,A ,C ,D ;
(2)连接线段BD、OD,试求三角形BOD的面积;
(3)若长方形ABCD以每秒1个单位长度匀速向下运动,设运动的时间为t秒,问是否存在某一时刻,三角形BOD的面积与长方形ABCD的面积相等?若存在,请求出t的值;若不存在,请说明理由.
33.已知:如图,菱形ABCD的对角线AC,BD相交于O,点E,F分别是AD,DC的中点,已知OE=,EF=3,求菱形ABCD的周长和面积.
34.如图,在△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:四边形BDFG是菱形;
(2)若AG=11,CF=8,求四边形BDFG的周长.
35.如图,在△ABC中,AD、BE分别是边BC、AC上的中线,AD与BE交于点O,点F、G分别是BO、AO的中点,联结DE、EG、GF、FD.
(1)求证:FG∥DE;
(2)若AC=BC,求证:四边形EDFG是矩形.
36.(1)如图(1),已知:正方形ABCD的对角线交于点O,E是AC上的一动点,过点A作AG⊥BE于G,交BD于F.求证:OE=OF.
(2)在(1)的条件下,若E点在AC的延长线上,以上结论是否成立,为什么?
37.如图,已知点P为∠ACB平分线上的一点,∠ACB=60°,PD⊥CA于D,PE⊥CB于E.点M是线段CP上的动点(不与两端点C、P重合),连接DM,EM.
(1)求证:DM=ME;
(2)当点M运动到线段CP的什么位置时,四边形PDME为菱形,请说明理由.
38.如图,正方形ABCD的边长为2,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F.
(1)求证:AF=BE;
(2)求点E到BC边的距离.
39.菱形ABCD中,F是对角线AC的中点,过点A作AE⊥BC垂足为E,G为线段AB上一点,连接GF并延长交直线BC于点H.
(1)当∠CAE=30°时,且CE=,求菱形的面积;
(2)当∠BGF+∠BCF=180°,AE=BE时,求证:BF=(+1)GF.
40.如图,P为正方形ABCD边BC上任一点,BG⊥AP于点G,在AP的延长线上取点E,使AG=GE,连接BE、CE,作DM⊥AG于M.
(1)求证:DM=AG;
(2)若△BCE是等边三角形,连DE,△ADE的面积为25,求BG长.
41.如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD,BE,BC于点P,O,Q,连接BP,EQ.
(1)求证:四边形BPEQ是菱形;
(2)F为AB的中点,则线段OF与线段AE有什么位置关系和数量关系?直接写出结论,不必证明.
(3)在(2)的条件下,若AB=6,OF=4,求PQ的长.
42.如图,在△ABC中,BD、CE分别为AC、AB边上的中线,BD、CE交于点H,点G、F分别为HC、HB的中点,连接AH、DE、EF、FG、GD,其中HA=BC.
(1)证明:四边形DEFG为菱形;
(2)猜想当AC、AB满足怎样的数量关系时,四边形DEFG为正方形,并说明理由.
43.在菱形ABCD中,AC是对角线,CD=CE,连接DE,点M是线段DE的中点.
(1)如图1,连接CM,若AC=16,CD=10,求DE的长;
(2)如图2,点F在菱形的外部,DF=DM,且∠CDA=∠FDE,连接FM交AD于点G,FM的延长线交AC于点N,求证:CN=AG.
44.在菱形ABCD中,∠C=60°,E为CD边上的点,连接BE.
(1)如图1,若E为CD的中点且BE=3,求菱形ABCD的面积.
(2)如图2,点F在BC边上,且DE=CF,连接DF交BE于点M,连接EB并延长至点N,使得BN=DM,求证:AN=DM+BM.
45.正方形ABCD中,点P是边CD上的任意一点,连接BP,O为BP的中点,作PE⊥BD于E,连接EO,AE.
(1)若∠PBC=α,求∠POE的大小(用含α的式子表示);
(2)用等式表示线段AE与BP之间的数量关系,并证明.
46.边长为a的正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连结CE.
(1)若点F在边BC上(如图);
①求证:CE=EF;
②若BC=2BF,求DE的长.
(2)若点F在CB延长线上,BC=2BF,请直接写出DE的长.
浙教新版八年级下学期《第5章 特殊平行四边形》2019年单元测试卷
参考答案与试题解析
一.解答题(共46小题)
1.已知:(x﹣2)2+(5﹣x)2=.若把x﹣2与5﹣x看成一个长方形的长和宽,求这个长方形的周长和面积.
【分析】根据矩形的周长公式和矩形的面积公式解答即可.
【解答】解:周长=2(x﹣2+5﹣x)=6.
由2(x﹣2)(5﹣x)=[(x﹣2)+(5﹣x)]2﹣[(x﹣2)2+(5﹣x)2]=知,
面积=(x﹣2)(5﹣x)=.
【点评】考查了矩形的性质,求矩形的面积时,需要利用完全平方公式的变形公式,难度不大.
2.如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.
(1)如图1,若点E为线段AM的中点,BM:CM=1:2,BE=,求AB的长;
(2)如图2.若G为AE中点,延长DG至N,使DG=NG,连接EN,且∠EDG=∠ENG.求证:BF+DF=AF.
【分析】(1)设BM=x,则MC=2x,由此得到AB=BC=3x,在Rt△ABM中,根据直角三角形斜边上的中线等于斜边的一半,可求AM长,再利用勾股定理可求AB长;
(2)要证明的三条线段没有组成一个三角形或一条线段,所以延长FD交过点A作垂直于AF的直线于H点,证明△ABF≌△ADH,把BF转化到DH,从而三条线段放在了等腰直角三角形中便解决了问题.
【解答】解:(1)设BM=x,则CM=2x,BC=3x,
∵BA=BC,∴BA=3x.
在Rt△ABM中,E为斜边AM中点,
∴AM=2BE=2.
由勾股定理可得AM2=MB2+AB2,
即40=x2+9x2,解得x=2.
∴AB=3x=6.
(2)∵∠EDG=∠ENG,
∴DE=EN,
∵DG=NG,
∴AE⊥DN,
∵G为AE中点,
∴DA=DE,延长FD交过点A作垂直于AF的直线于H点,
∵DF平分∠CDE,
∴∠1=∠2.
∵DE=DA,DG⊥AF,
∴∠3=∠4.
∵∠1+∠2+∠3+∠4=90°,
∴∠2+∠3=45°.
∴∠DFG=90°﹣45°=45°.
∴AH=AF.
∵∠BAF+∠DAF=90°,∠HAD+∠DAF=90°,
∴∠BAF=∠DAH.
又AB=AD,
∴△ABF≌△ADH(SAS).
∴AF=AH,BF=DH.
∵Rt△FAH是等腰直角三角形,
∴HF=AF.
∵HF=DH+DF=BF+DF,
∴BF+DF=AF.
【点评】本题主要考查了正方形的性质、全等三角形的判定和性质以及等腰三角形的性质、勾股定理,综合性较强,正确作出辅助线,把三条线段转化到一个等腰直角三角形是解题的关键.
3.已知菱形ABCD,E为AD上一点,且BA=BE,连接BD.
(1)如图1,过B作BF⊥AD,垂足为F,若BD=2,DE=1,求菱形ABCD的边长.
(2)如图2,点M为边CD上一点,连接BM,且∠CBM=∠DBE,过E作EG⊥BM,垂足为G点,O为BD中点,连接GO并延长交BE于H点,交AD于N点,求证AN=EN.
【分析】(1)由条件给的两条线段长度并不能直接求出菱形边长,故需要设未知数列方程间接求解.由BA=BE,BF⊥AD可得AF=EF,设菱形边长为x,则AF=EF=,DF=.观察Rt△BEF与Rt△BDF根据勾股定理列出两等式,再以BF为等量关系列方程,即能求出x.
(2)由∠CBM=∠DBE易得∠CBD=∠EBM,且∠CBD与∠EBM有一边相等,考虑到一边一角相等的情况,把BM延长到P使BP=BD即得到全等的△BEP与△BCD,所以BE=EP即△BEP是等腰三角形,加上EG⊥BM即有G未BP中点.又O为BD中点,根据中位线定理有OG∥DP,所以有同位角相等,进而证得BG=BO.证明△BGH≌△DON得BH=DN即EH=AN,再根据全等三角形对应角相等和对顶角相等证得EN=EH,最后得证AN=EN.
【解答】解:(1)设菱形ABCD边长为x
∴AD=AB=BE=x
∵DE=1
∴AE=AD﹣DE=x﹣1
∵BF⊥AD于F,AB=BE
∴∠BFE=90°,AF=EF=AE=
∴DF=AD﹣AF=x﹣=
∵BF2+EF2=BE2,BF2+DF2=BD2
∴BF2=BE2﹣EF2=BD2﹣DF2
∵BD=2
∴
解得:x1=﹣4(舍去),x2=3
∴菱形ABCD 的边长等于3
(2)证明:延长BM到P,使BP=BD,连接DP、EP
∴∠BPD=∠BDP
∵菱形ABCD中,AB=BE
∴BE=AB=BC=CD=AD,AD∥BC
∴∠ADB=∠ABD=∠CBD
∵∠CBM=∠DBE
∴∠CBM+∠MBD=∠DBE+∠MBD
即∠CBD=∠EBP
在△BEP与△BCD中
∴△BEP≌△BCD(SAS)
∴PE=CD
∴PE=BE
∵EG⊥BM
∴G为BP中点
∵O为BD中点
∴OG为△BDP中位线,OG∥PD
∴∠BGO=∠BPD,∠BOG=∠BDP
∴∠BGO=∠BOG
∴∠DON=∠BGO=∠BOG,BG=OB
∴DO=BO=BG
在△BGH与△DON中,
∴△BGH≌△DON(ASA)
∴BH=DN,∠BHG=∠DNO
∴BE﹣BH=AD﹣DN
即EH=AN
∵∠EHN=∠BHG
∴∠EHN=∠DNO
∴EN=EH
∴AN=EN
【点评】本题考查了菱形的性质,勾股定理,解一元二次方程,等腰三角形性质,全等三角形的判定和性质,中位线定理.第(1)题的解题关键是在不能直接求得线段时,利用设未知数列方程的方法间接求,利用勾股定理作为等量关系,是勾股定理应用的常见题型.第(2)题的解题关键是如何发现给出条件之间的联系和使用,注意角度和线段长度的等量代换,层层推进解题思路.
4.在四边形ABCD中,对角线AC、BD相交于点O,过点O的两条直线分别交边AB、CD、AD、BC于点E、F、G、H.
【感知】如图①,若四边形ABCD是正方形,且AG=BE=CH=DF,则S四边形AEOG= S正方形ABCD;
【拓展】如图②,若四边形ABCD是矩形,且S四边形AEOG=S矩形ABCD,设AB=a,AD=b,BE=m,求AG的长(用含a、b、m的代数式表示);
【探究】如图③,若四边形ABCD是平行四边形,且AB=3,AD=5,BE=1,试确定F、G、H的位置,使直线EF、GH把四边形ABCD的面积四等分.
【分析】【感知】如图①,根据正方形的性质和全等三角形的性质即可得到结论;
【拓展】如图②,过O作ON⊥AD于N,OM⊥AB于M,根据图形的面积得到mb=AG?a,于是得到结论;
【探究】如图③,过O作KL⊥AB,PQ⊥AD,则KL=2OK,PQ=2OQ,根据平行四边形的面积公式得到=,根据三角形的面积公式列方程即可得到结论.
【解答】解:【感知】如图①,
∵四边形ABCD是正方形,
∴∠OAG=∠OBE=45°,OA=OB,
在△AOG与△BOE中,,
∴△AOG≌△BOE,
∴S四边形AEOG=S△AOB=S正方形ABCD;
故答案为:;
【拓展】如图②,过O作ON⊥AD于N,OM⊥AB于M,
∵S△AOB=S矩形ABCD,S四边形AEOG=S矩形ABCD,
∴S△AOB=S四边形AEOG,
∵S△AOB=S△BOE+S△AOE,S四边形AEOG=S△AOG+S△AOE,
∴S△BOE=S△AOG,
∵S△BOE=BE?OM=mb=mb,S△AOG=AG?ON=AG?a=AG?a,
∴mb=AG?a,
∴AG=;
【探究】如图③,过O作KL⊥AB,PQ⊥AD,
则KL=2OK,PQ=2OQ,
∵S平行四边形ABCD=AB?KL=AD?PQ,
∴3×2OK=5×2OQ,
∴=,
∵S△AOB=S平行四边形ABCD,S四边形AEOG=S平行四边形ABCD,
∴S△AOB=S四边形AEOG,
∴S△BOE=S△AOG,
∵S△BOE=BE?OK=×1×OK,S△AOG=AG?OQ,
∴×1×OK=AG?OQ,∴=AG=,
∴当AG=CH=,BE=DF=1时,直线EF、GH把四边形ABCD的面积四等分.
【点评】本题考查了正方形、矩形、平行四边形的性质及三角形、四边形的面积问题,认真阅读材料,理解并证明S△BOE=S△AOG是解决问题的关键.
5.如图,平行四边形ABCD,F是对角线AC上的一点,过点D作DE∥AC,且DE=CF,连接AE、DE、EF.
(1)求证:△ADE≌△BCF;
(2)若∠BAF+∠AED=180°,求证:四边形ABFE为菱形.
【分析】(1)根据平行四边形的性质和全等三角形的判定证明即可;
(2)根据平行四边形的判定和菱形的判定解答即可.
【解答】证明:(1)∵平行四边形ABCD,
∴AD=BC,AD∥BC,
∴∠DAC=∠BCF,
∵DE∥AC,
∴∠DAC=∠EDA,
∴∠FCB=∠EDA,
在△ADE与△BCF中
,
∴△ADE≌△BCF(SAS);
(2)∵DE∥AC,且DE=AC,
∴四边形EFCD是平行四边形,
∴DC=EF,且DC∥EF,
又∵AB=CD,AB∥CD,
∴AB=EF,AB∥EF,
∴四边形ABFE是平行四边形,
∵△ADE≌△BCF,
∴∠AED=∠BFC,
∵∠BAF+∠AED=180°,
∴∠BAF+∠BFC=180°,
又∠BFA+∠BFC=180°,
∴∠BAF=∠BFA,
∴BA=BF,
∴四边形ABFE为菱形.
【点评】此题考查菱形的判定,关键是根据平行四边形的判定、菱形的判定和全等三角形的判定解答.
6.菱形ABCD中,∠ABC=60°,点E在AD上,连接BE,点F、H在BE上,△AFH为等边三角形.
(1)如图1,若CE⊥AD,BE=,求菱形ABCD的面积;
(2)如图2,点G在AC上,连接FG,HC,若FG∥AH,HC=2AH,求证:AG=GC.
【分析】(1)首先证明△ABC,△ADC都是等边三角形,由CE⊥AD,推出AE=DE,BC⊥CE,设AE=DE=m,则AD=BC=2m,CE=m,在Rt△BCE中,根据BE2=CE2+BC2,构建方程求出m即可解决问题;
(2)作CK∥AH交BE于点K.想办法证明FH=FK,利用平行线分线段成比例定理即可解决问题;
【解答】(1)解:如图1中,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠ABC=∠D=60°,AD∥BC
∴△ABC,△ADC都是等边三角形,
∵CE⊥AD,
∴AE=DE,BC⊥CE,设AE=DE=m,则AD=BC=2m,CE=m,
在Rt△BCE中,∵BE2=CE2+BC2,
∴4m2+3m2=63,
∴m=±3,
∵m>0,
∴m=3,
∴BC=6,EC=3,
∴S菱形ABCD=BC?CE=18.
(2)作CK∥AH交BE于点K.
∵△AFH是等边三角形,
∴∠AHF=∠AFH=60°,
∵AH∥CK,
∴∠AHF=∠CKE=60°,
∴∠AFB=∠BKC=120°,
∵∠ABF+∠CBK=60°,∠CBK+∠BCK=60°,
∴∠ABF=∠BCK,
∵AB=BC,
∴△ABF≌△BCK(AAS),
∴BK=AF,
∵∠BAC=∠FAH=60°,
∴∠BAF=∠CAH,
∵BA=AC,AF=AH,
∴△BAF≌△CAH(SAS),
∴BF=CH,
∵CH=2AH,AH=AF=FH=BK,
∴BK=FK=FH,
∵AH∥FG∥CK,FH=FK,
∴AG=CG.
【点评】本题考查菱形的性质、等边三角形的判定和性质、全等三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,正确寻找全等三角形解决问题,属于中考常考题型.
7.已知:在平行四边形ABCD中,点O是边AD的中点,连接CO并延长交BA延长线于点E,连接ED、AC.
(1)如图1,求证:四边形AEDC是平行四边形;
(2)如图2,若四边形AEDC是矩形,请探究∠COD与∠B的数量关系,写出你的探究结论,并加以证明.
【分析】(1)由题意可证△AEO≌△DCO,可得AE=CD,且AE∥CD,则四边形AEDC是平行四边形;
(2)由矩形的性质可得OC=OD=OA=OE,可得∠ADC=∠OCD,根据三角形内角和为180°,可得∠COD与∠B的数量关系.
【解答】证明:(1)∵四边形ABCD是平行四边形
∴AB∥CD
∴∠BEC=∠DCE
∵点O是边AD的中点
∴AO=DO,且∠BEC=∠DCE,∠AOE=∠DOC
∴△AEO≌△DCO(AAS)
∴AE=CD
∵AE∥DC,AE=CD
∴四边形AEDC是平行四边形
(2)∠COD=180°﹣2∠B
理由如下:
∵四边形ABCD是平行四边形
∴∠B=∠ADC
∵四边形AEDC是矩形
∴AO=EO=CO=DO
∴∠ADC=∠OCD
∵∠ADC+∠OCD+∠COD=180°
∴∠COD=180°﹣2∠ADC=180°﹣2∠B
【点评】本题考查了矩形的性质,平行四边形的性质和判定,熟练运用这些性质进行推理是本题的关键.
8.如图1,P为正方形ABCD内一点,且PA:PB:PC=1:2:3,求∠APB的度数.
小明同学的想法是:不妨设PA=x,PB=2x,PC=3x,设法把PA、PB、PC相对集中,于是他将△BCP绕点B顺时针旋转90°得到△BAE(如图2),然后连结PE,问题得以解决.请你回答图2中∠APB= 135 度.
请你参考小明同学的方法,解答下列问题.
如图3,P是等边△ABC内一点,PA:PB:PC=3:4:5,那么∠APB= 150 度.请写出推理过程.
【分析】图2中,根据旋转的性质知△BCP≌△BAE.由全等三角形的对应边相等、等腰三角形的判定推知△BPE是等腰三角形,则∠BPE=∠BEP=45°;然后由全等三角形的对应边相等、勾股定理证得∠APE=90°;最后根据图中角与角间的数量关系求得∠APB=135°;
如图3,将△BCP绕点B顺时针旋转60°得到△ABM,然后连接PM,根据旋转的性质知∠PBM=60°,△BCP≌△BMA.推出△PBM是等边三角形,得到∠BPM═∠PBM=60°,根据勾股定理的逆定理得到∠APM=90°,于是得到结论.
【解答】解:如图2.
∵根据旋转的性质知∠PBE=90°,△BCP≌△BAE,
∴BP=BE,PC=AE,
∴∠BPE=∠BEP=45°,PE=PB,
又PA:PB:PC=1:2:3,
设PA=x,PB=2x,PC=3x,
∴AE=PC=3x,AP=x,PE=2x,
∴AE2=AP2+PE2,
∴∠APE=90°,
∴∠APB=∠APE+∠BPE=90°+45°=135°,
即图2中∠APB的度数为135°.
故答案是:135;
如图3,将△BCP绕点B顺时针旋转60°得到△ABM,然后连接PM,
∵根据旋转的性质知∠PBM=60°,△BCP≌△BMA.
∴PB=BM,
∴△PBM是等边三角形,
∴∠BPM═∠PBM=60°,
∵PA:PB:PC=3:4:5,
∴PA=3x,PB=4x,PC=5x,
∴AM=PC=5x,BM=PB=PM=4x,PA=3x,
∴AM2=PA2+PM2,
∴∠APM=90°,
∴∠APB=90°+60°=150°
∴PA:PB:PC=3:4:5,那么∠APB=150度,
故答案是:150.
【点评】本题综合考查了旋转的性质,等边三角形和正方形的性质以及全等三角形的判定与性质等知识点.旋转变化前后,对应角、对应线段分别相等,图形的大小、形状都不变.
9.(1)如图①,分别以△ABC的边AB、AC为一边向形外作正方形ABDE和正方形ACGF.求证S△AEF=S△ABC.
(2)如图②,分别以△ABC的边AB、AC、BC为边向形外作正方形ABDE、ACGF、BCHI,可得六边形DEFGHI,若S正方形ABDE=17,S正方形ACGF=25,S正方形BCHI=16,求S六边形DEFGHI.
【分析】(1)作辅助线,证明△AMC≌△ANF(AAS),得CM=FN根据三角形面积公式可得结论;
(2)同理得:S△AEF=S△ABC=S△BDI=S△CHG,设BO=x,则CO=4﹣x,根据勾股定理列方程得:17﹣x2=25﹣(4﹣x)2,解得:x=1,根据面积和可得S六边形DEFGHI.
【解答】证明:(1)如图①,过点C作CM⊥AB,过F作FN⊥EA与EA的延长线交于点N,
∴∠CMA=∠ANF=90°,
∵四边形ABDE和四边形ACGF是正方形,
∴AB=AE,AC=AF,∠BAE=∠CAF=90°,
∴∠CAM+∠CAN=∠FAN+∠CAN=90°,
∴∠CAM=∠FAN,
在△AMC和△ANF中,
∵,
∴△AMC≌△ANF(AAS),
∴CM=FN,
∴AE?FN=,
∴S△AEF=S△ABC.
(2)由上题结论得:S△AEF=S△ABC=S△BDI=S△CHG,
由题意得:AB=,AC=5,BC=4,
过点O作AO⊥BC,设BO=x,则CO=4﹣x,
在Rt△ABO和Rt△ACO中,
AO2=AB2﹣BO2=AC2﹣CO2,
即17﹣x2=25﹣(4﹣x)2,
解得:x=1,
∴AO=4,
S六边形DEFGHI=S正方形ABDE+S正方形BCHI+S正方形ACGF+S△AEF+S△BDI+S△CHG+S△ABC,
=17+25+16+4××4×4,
=90.
【点评】本题考查正方形的性质,三角形和多边形的面积等知识,解题的关键是理解题意,恰当作辅助线,学会利用面积和求六边形面积,属于中考常考题型.
10.如图1,点E为正方形ABCD的边AB上一点,EF⊥EC,且EF=EC,连接AF.
(1)求∠EAF的度数;
(2)如图2,连接FC交BD于M,交AD于N.求证:BD=AF+2DM.
【分析】(1)过点F作FM⊥AB并交AB的延长线于点M,只要证明△EBC≌△FME(AAS)即可解决问题;
(2)过点F作FG∥AB交BD于点G.首先证明四边形ABGF为平行四边形,再证明△FGM≌△DMC(AAS)即可解决问题;
【解答】(1)解:过点F作FM⊥AB并交AB的延长线于点M,
∵四边形ABCD是正方形,
∴∠B=∠M=∠CEF=90°,
∴∠MEF+∠CEB=90°,∠CEB+∠BCE=90°,
∴∠MEF=∠ECB,
∵EC=EF,
∴△EBC≌△FME(AAS)
∴FM=BE
∴EM=BC
∵BC=AB,
∴EM=AB,
∴EM﹣AE=AB﹣AE
∴AM=BE,
∴FM=AM,
∵FM⊥AB,
∴∠MAF=45°,
∴∠EAF=135°.
(2)证明:过点F作FG∥AB交BD于点G.
由(1)可知∠EAF=135°,
∵∠ABD=45°
∴∠EAF=135°+∠ABD=180°,
∴AF∥BG,
∵FG∥AB,
∴四边形ABGF为平行四边形,
AF=BG,FG=AB,
∵AB=CD,
∴FG=CD,
∵AB∥CD,
∴FG∥CD,
∴∠FGM=∠CDM,
∵∠FMG=∠CMD
∴△FGM≌△DMC(AAS),
∴GM=DM,
∴DG=2DM,
∴BD=BG+DG=AF+2DM.
【点评】本题考查全等三角形的判定和性质、正方形的性质、平行四边形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
11.如图(1),在Rt△ABC,∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连结AD、CF,AD与CF交于点M.
(1)求证:△ABD≌△FBC;
(2)如图(2),求证:AM2+MF2=AF2.
【分析】(1)根据四边形ABFG、BCED是正方形得到两对边相等,一对直角相等,根据图形利用等式的性质得到一对角相等,利用SAS即可得到三角形全等;
(2)根据全等三角形的性质和勾股定理即可得到结论.
【解答】解:(1)∵四边形ABFG、BCED是正方形,
∴AB=FB,CB=DB,∠ABF=∠CBD=90°,
∴∠ABF+∠ABC=∠CBD+∠ABC,
即∠ABD=∠CBF,
在△ABD和△FBC中,,
∴△ABD≌△FBC(SAS);
(2)∵△ABD≌△FBC,
∴∠BAD=∠BFC,
∴∠AMF=180°﹣∠BAD﹣∠CNA=180°﹣(∠BFC+∠BNF)=180°﹣90°=90°,
∴AM2+MF2=AF2.
【点评】此题考查了全等三角形的判定与性质,正方形的性质,勾股定理,熟练掌握全等三角形的判定定理是解题的关键.
12.如图,DE是平行四边形ABCD中∠ADC的角平分线,EF∥AD交DC于F.
(1)如图1,求证:四边形AEFD是菱形;
(2)如图2,连接FB,FB⊥AB,若∠DAB=60°,FC=2,请直接写出所有长度为4的线段.
【分析】(1)由题意可证四边形AEFD是平行四边形,由DE平分∠ADC,可得∠ADE=∠FDE=∠AED,可得AD=AE,即可证四边形AEFD是菱形;
(2)由题意可得∠C=DAB=60°,可求BC=4,根据平行四边形的性质和菱形的性质可得AD=DF=AE=EF=BC=4.
【解答】解:(1)∵四边形ABCD是平行四边形
∴DF∥AE,AD=BC
∵EF∥AD,DF∥AE
∴四边形AEFD是平行四边形
∵DE平分∠ADC
∴∠ADE=∠FDE
∵DF∥AE
∴∠FDE=∠AED
∴∠ADE=∠AED
∴AD=AE且四边形AEFD是平行四边形
∴四边形AEFD是菱形
(2)∵FB⊥AB,DC∥AB
∴∠BFC=90°
∵四边形ABCD是平行四边形,
∴∠DAB=∠C,且∠DAB=60°
∴∠C=60°
∴∠FBC=30°
∴BC=2FC=4
∴AD=BC=4
∵四边形AEFD是菱形
∴AD=DF=EF=AE=4
∴长度为4的线段有:AD,DF,EF,AE,BC
【点评】本题菱形的性质和判定,平行四边形的性质,熟练运用这些性质解决问题是本题的关键.
13.已知:分别以△ABC的各边为边,在BC边的同侧作等边三角形ABE、等边三角形CBD和等边三角形ACF,连结DE,DF.
(1)试说明四边形DEAF为平行四边形.
(2)当△ABC满足什么条件时,四边形DEAF为矩形?并说明理由;
(3)当△ABC满足什么条件时,四边形DEAF为菱形.直接写出答案 AB=AC .
【分析】(1)根据等边三角形的性质得∠ABE=∠CBD=60°,AB=BE=AE,CB=BD=CD,则∠ABC=∠EBD,于是可利用“SAS”判断△ABC≌△EBD,得到AC=DE,再由△ACF为等边三角形得AC=AF,则AF=DE,同理可证△ACB≌△FCD得到AB=DF,则AE=DF,然后根据平行四边形的判定方法即可得到结论;
(2)由于四边形DEAF是平行四边形,当∠EAF=90°时,四边形DEAF为矩形,根据等边三角形角的大小,可得∠BAC=150°;
(3)由于四边形DEAF是平行四边形,根据菱形的判定方法,当AE=AF时,四边形DEAF是菱形,此时AB=AC.
【解答】解:(1)如图1,∵△ABE和△CBD为等边三角形,
∴∠ABE=∠CBD=60°,AB=BE=AE,CB=BD=CD,
∴∠ABC=∠EBD,
在△ABC和△EBD中
,
∴△ABC≌△EBD(SAS),
∴AC=DE,
∵△ACF为等边三角形,
∴AC=AF,
∴AF=DE,
同理可证得△ACB≌△FCD,
∴AB=DF,
而AB=AE,
∴AE=DF,
∴四边形DEAF是平行四边形;
(2)如图2,当△ABC满足∠BAC=150°时,四边形DEAF是矩形.理由如下:
由(1)知:四边形DEAF是平行四边形,
∵∠BAC=150°,∠EAB=∠FAC=60°
∴∠EAF=360°﹣150°﹣60°﹣60°=90°
∴四边形DEAF是矩形;
(3)如图3,△ABC满足AB=AC时,四边形DEAF是菱形.理由如下:
由(1)知:四边形DEAF是平行四边形,
∵AB=AC,AE=AB,AC=AF,
∴AE=AF,
∴四边形DEAF是菱形.
故答案为:AB=AC.
【点评】本题考查了菱形的判定:一组邻边相等的平行四边形是菱形(平行四边形+一组邻边相等=菱形);四条边都相等的四边形是菱形;对角线互相垂直的平行四边形是菱形(或“对角线互相垂直平分的四边形是菱形”).也考查了全等三角形的判定与性质、等边三角形的性质和平行四边形、矩形的判定.
14.在正方形ABCD中,∠C=∠D=90°,点E、F分别是边CD、BC上的中点,点P是一动点.记∠DEP=∠1,∠BFP=∠2,∠EPF=∠α.
(1)如图1,若点P运动到线段AD中点时,∠α= 45° ,∠1+∠2= 135° .
(2)如图2,若点P在线段AD上运动时,∠1、∠2和∠α之间有何关系?
(3)当点P在直线AD上(在线段AD之外且PE与PF不重合)运动时,∠1、∠2和∠α之间又有何关系?说明理由.
【分析】(1)只要证明△PDE是等腰直角三角形,四边形CDPF是矩形即可解决问题;
(2)连接PC.利用三角形的外角的性质即可解决问题;
(3)分三种情形分别求解即可;
【解答】解:(1)如图1中,
∵四边形ABCD是正方形,
∴∠D=90°,AD=BC=DC,AD∥BC,
∵PA=PD,DE=EC,BF=FC,
∴PD=DE,
∴∠1=45°,
∵PD=FC,PD∥FC,
∴四边形CDPF是平行四边形,
∵∠D=90°,
∴四边形CDPF是矩形,
∴PF∥CD,∠PFC=90°,
∴∠α=∠1=45°,∠2=90°,
∴∠1+∠2=135°,
故答案为45°,135°.
(2)如图2中,连接PC.
∵∠1=∠EPC+∠ECP,∠2=∠FPC+∠FCP,
∴∠1+∠2=∠EPC+∠FPC+∠ECP+∠FCP=∠α+90°.
(3)如图:
①当点P在线段DA的延长线上时,由(2)可知:∠1+∠2=∠α+90°.
②当点P在线段AD的延长线上且在直线EF的上方时,
∵∠2=∠α+∠PKF,∠PKF=90°+∠KEC=90°+∠1,
∴∠2=∠α+∠1+90°.
③当点P在直线EF的下方时,设PF交CD于K.
∵∠2=90°+∠FKC=90°+∠PKE=90°+(∠1﹣∠α),
∴∠2=90°+∠1﹣∠α.
【点评】本题考查正方形的性质、平行线的判定和性质、三角形的外角的性质等知识,解题的关键是熟练掌握基本知识,学会用分类讨论的思想思考问题,属于中考常考题型.
15.如图,在菱形ABCD中,∠B=60°.
(1)如图①,若点E、F分别在边AB、AD上,且BE=AF.求证:△CEF是等边三角形;
(2)小明发现若点E、F分别在边AB、AD上,且∠CEF=60°时△CEF也是等边三角形,并通过画图验证了猜想;小丽通过探索,认为应该以CE=EF为突破口构造两个三角形全等;小倩受到小丽的启发,尝试在BC上截取BM=BE,连接ME,如图②,很快就证明了△CEF是等边三角形,请你根据小倩的方法,写出完整的证明过程.
【分析】(1)想办法证明△BEC≌△AFC(SAS),即可解决问题;
(2)想办法证明△ECM≌△FEA(ASA),即可解决问题;
【解答】(1)证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵∠B=60°,
∴△ABC,△ADC都是等边三角形,
∴∠B=∠CAF=∠ACB=60°,
∵BC=AC,BE=AF,
∴△BEC≌△AFC(SAS),
∴CE=CF,∠BCE=∠ACF,
∴∠ECF=∠BCA=60°,
∴△ECF是等边三角形.
(2)证明:∵BE=BM,∠B=60°,
∴△BEM是等边三角形,
∴∠EMB=∠BEM=60°,∠EMC=∠AEM=120°,
∵AB=BC,∠EAF=120°,
∴AE=CM,∠EAF=∠EMC,
∵∠FEC=60°,
∴∠AEF+∠CEM=60°,
∵∠CEM+∠ECM=60°,
∴∠AEF=∠ECM,
∴△ECM≌△FEA(ASA),
∴EF=EC,∵∠FEC=60°,
∴△EFC是等边三角形.
【点评】本题考查菱形的性质、等边三角形的判定和性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题.
16.如图1,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形ABCD的外角∠DCG的平分线CF于点F.
(1)如图2,取AB的中点H,连接HE,求证:AE=EF.
(2)如图3,若点E是BC的延长线上(除C点外)的任意一点,其他条件不变结论“AE=EF”仍然成立吗?如果正确,写出证明过程:如果不正确,请说明理由.
【分析】(1)取AB的中点H,连接EH,根据已知及正方形的性质利用ASA判定△AHE≌△ECF,从而得到AE=EF;
(2)成立,延长BA到M,使AM=CE,根据已知及正方形的性质利用ASA判定△AHE≌△ECF,从而得到AE=EF;
【解答】(1)证明:取AB的中点H,连接EH;如图1所示
∵四边形ABCD是正方形,AE⊥EF;
∴∠1+∠AEB=90°,∠2+∠AEB=90°
∴∠1=∠2,
∵BH=BE,∠BHE=45°,且∠FCG=45°,
∴∠AHE=∠ECF=135°,AH=CE,
在△AHE和△ECF中,
,
∴△AHE≌△ECF(ASA),
∴AE=EF;
(2)解:AE=EF成立,
理由如下:如图2,延长BA到M,使AM=CE,
∵∠AEF=90°,
∴∠FEG+∠AEB=90°.
∵∠BAE+∠AEB=90°,
∴∠BAE=∠FEG,
∴∠MAE=∠CEF.
∵AB=BC,
∴AB+AM=BC+CE,
即BM=BE.
∴∠M=45°,
∴∠M=∠FCE.
在△AME与△ECF中,
,
∴△AME≌△ECF(ASA),
∴AE=EF.
【点评】本题考查正方形的性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
17.如图,四边形ABCD和四边形CEFG都是正方形,且BC=CD,CE=CG,∠BCD=∠GCE=90°.
(1)求证:△BCG≌△DCE;
(2)求证:BG⊥DE.
【分析】(1)根据正方形的性质和全等三角形的判定证明即可;
(2)利用全等三角形的性质和三角形内角和解答即可.
【解答】证明:(1)∵∠BCD=∠GCE=90°,
∴∠BCG=∠DCE,
在△BCG与△DCE中
,
∴△BCG≌△DCE(SAS);
(2)∵△BCG≌△DCE,
∴∠HBC=∠ODH,
∵∠BHC=∠DHO,
∵∠HBC+∠BHC=90°,
∴∠ODH+∠DHO=90°,
∴∠DOH=90°,
∴BG⊥DE.
【点评】本题考查三角形全等的判定和性质和正方形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
18.已知:在正方形ABCD和正方形DEFG中,顶点B、D、F在同一直线上,H是BF的中点.
(1)如图①,若AB=1,DG=2,求BH的长;
(2)如图②,连接AH、GH,求证:AH=GH且AH⊥GH.
【分析】(1)先根据勾股定理得出AB,DG,进而求出BF,即可得出结论;
(2)证法一、先判断△ABH≌△MFH,进而判断出△ADG≌△MFG.即可判断出△AGM为等腰直角三角形,即可得出结论;
证法二、先判断出MN=BF.进而判断出△AMH≌△HNG,即可判断出∠AHM+∠GHN=90°.即可得出结论.
【解答】(1)解:∵正方形中ABCD和正方形DEFG,
∴△ABD,△GDF为等腰直角三角形.
∵AB=1,DG=2,
∴由勾股定理得BD=,DF=2.
∵B、D、F共线,
∴BF=3.
∵H是BF的中点,
∴BH=BF=
(2)证法一:
如图1,延长AH交EF于点M,连接AG,GM,
∵正方形中ABCD和正方形DEFG且B、D、F共线,
∴AB∥EF.
∴∠ABH=∠MFH.
又∵BH=FH,∠AHB=∠MHF,
∴△ABH≌△MFH.
∴AH=MH,AB=MF.
∵AB=AD,
∴AD=MF.
∵DG=FG,∠ADG=∠MFG=90°,
∴△ADG≌△MFG.
∴∠AGD=∠MGF,AG=MG.
又∵∠DGM+∠MGF=90°,
∴∠AGD+∠DGM=90°.
∴△AGM为等腰直角三角形.
∵AH=MH,
∴AH=GH,AH⊥GH.
证法二:
如图2,连接AC,GE分别交BF于点M,N,
∵正方形中ABCD和正方形DEFG且B、D、F共线,
∴AC⊥BF,GE⊥BF,DM=BD,DN=DF.
∴∠AMD=∠GNH=90°,MN=BF.
∵H是BF的中点,
∴BH=BF.
∴BH=MN.
∴BH﹣MH=MN﹣MH.
∴BM=HN.
∵AM=BM=DM,
∴AM=HN=DM.
∴MD+DH=NH+DH.
∴MH=DN.
∵DN=GN,
∴MH=GN.
∴△AMH≌△HNG.
∴AH=GH,∠AHM=∠HGN.
∵∠HGN+∠GHN=90°,
∴∠AHM+∠GHN=90°.
∴∠AHG=90°.
∴AH⊥GH.
∴AH=GH,AH⊥GH.
【点评】此题主要考查了正方形的性质,等腰直角三角形的判定和性质,全等三角形的判定和性质,解(1)的关键是求出BF,解(2)的关键是判断出△ABH≌△MFH和△AMH≌△HNG;是一道中等难度的中考常考题.
19.如图,点P是正方形ABCD的对角线AC上的一点,PM⊥AB,PN⊥BC,垂足分别为点M,N,求证:DP=MN.
【分析】连结PB,由正方形的性质得到BC=DC,∠BCP=∠DCP,接下来证明△CBP≌△CDP,于是得到DP=BP,然后证明四边形BNPM是矩形,由矩形的对角线相等可得到BP=MN,从而等量代换可证得问题的答案.
【解答】证明:如图,连结PB.
∵四边形ABCD是正方形,
∴BC=DC,∠BCP=∠DCP=45°.
∵在△CBP和△CDP中,
,
∴△CBP≌△CDP(SAS).
∴DP=BP.
∵PM⊥AB,PN⊥BC,∠MBN=90°
∴四边形BNPM是矩形.
∴BP=MN.
∴DP=MN.
【点评】本题主要考查的是正方形的性质、全等三角形的性质和判定、矩形的性质和判定,证得四边形BFPE为矩形是解题的关键.
20.如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.
【分析】(1)依据矩形的性质,即可得出△AEG≌△CFH,进而得到GE=FH,∠CHF=∠AGE,由∠FHG=∠EGH,可得FH∥GE,即可得到四边形EGFH是平行四边形;
(2)由菱形的性质,即可得到EF垂直平分AC,进而得出AF=CF=AE,设AE=x,则FC=AF=x,DF=8﹣x,依据Rt△ADF中,AD2+DF2=AF2,即可得到方程,即可得到AE的长.
【解答】解:(1)∵矩形ABCD中,AB∥CD,
∴∠FCH=∠EAG,
又∵CD=AB,BE=DF,
∴CF=AE,
又∵CH=AG,
∴△AEG≌△CFH,
∴GE=FH,∠CHF=∠AGE,
∴∠FHG=∠EGH,
∴FH∥GE,
∴四边形EGFH是平行四边形;
(2)如图,连接EF,AF,
∵EG=EH,四边形EGFH是平行四边形,
∴四边形GFHE为菱形,
∴EF垂直平分GH,
又∵AG=CH,
∴EF垂直平分AC,
∴AF=CF=AE,
设AE=x,则FC=AF=x,DF=8﹣x,
在Rt△ADF中,AD2+DF2=AF2,
∴42+(8﹣x)2=x2,
解得x=5,
∴AE=5.
【点评】此题考查了菱形的性质、矩形的性质、全等三角形的判定与性质以及勾股定理的运用.注意准确作出辅助线是解此题的关键.
21.如图,四边形ABCD是正方形,AC与BD,相交于点O,点E、F是边AD上两动点,且AE=DF,BE与对角线AC交于点G,联结DG,DG交CF于点H.
(1)求证:∠ADG=∠DCF;
(2)联结HO,试证明HO平分∠CHG.
【分析】(1)根据题意可得△DFC≌△AFB,△AGB≌△ADG,可得∠ADG=∠DCF
(2)由题意可证CF⊥DG,由∠CHD=∠COD=90°,则D,F,O,C四点共圆,可得∠CDO=∠CHO=45°,可证OH平分∠CHG
【解答】证明(1)∵四边形ABCD是正方形
∴AB=AD=CD=BC,∠CDA=∠DAB=90°,∠DAC=∠CAB=45°,AC⊥BD
∵DC=AB,DF=AE,∠CDA=∠DAB=90°
∴△DFC≌△AEB
∴∠ABE=∠DCF
∵AG=AG,AB=AD,∠DAC=∠CAB=45°
∴△ADG≌△ABG
∴∠ADG=∠ABE
∴∠DCF=∠ADG
(2)∵∠DCF=∠ADG,且∠ADG+∠CDG=90°
∴∠DCF+∠CDG=90°
∴∠CHD=∠CHG=90°
∵∠CHD=∠COD
∴C,D,H,O四点共圆
∴∠CHO=∠CDO=45°
∴∠GHO=∠CHO=45°
∴HO平分∠CHG
【点评】本题考查了正方形的性质,全等三角形的判定和性质,灵活运用这些性质解决问题是本题的关键.
22.如图,已知AD是Rt△ABC斜边BC上的高,∠B的平分线交AD于M交AC于E,∠DAC的平分线交ME于O,交CD于N.求证:四边形AMNE是菱形.
【分析】根据全等三角形的判定和菱形的判定证明即可.
【解答】证明:∵BE平分∠ABC交AD于M,交AC于E,
∵∠ABE=∠DBM,
∵AD是Rt△ABC斜边BC上的高,
∴∠BAC=∠ADB=90°,
∴∠AEM=∠BMD,
∵∠AME=∠BMD,
∴∠AEM=∠AME,
∴AE=AM,
∵∠DAC的平分线交CD于N,
∴∠MAN=∠NAE,AN⊥ME,且AN平分ME,
在△BAO和△BNO中,
,
∴△ABO≌△NBO(ASA),
∴AO=NO,
∴AN和ME互相垂直平分,
∴四边形AMNE是菱形.
【点评】此题考查菱形的判定,关键是根据全等三角形的判定和性质解答.
23.如图,正方形ABCD的对角线AC,BD相交于点O,AB=3,E为OC上一点,OE=1,连接BE,过点A作AF⊥BE于点F,与BD交于点G.
(1)BE与AG相等吗?若相等,请证明,若不相等,请说明理由;
(2)求AF的长.
【分析】(1)利用正方形的性质得OA=OB,∠AOB=∠BOC=90°,再利用等角的余角相等得到∠AGO=∠BEO,则利用”AAS“可判断△AOG≌△BOE,然后根据全等三角形的性质得到结论;
(2)根据面积法列式可得AF的长.
【解答】解:(1)BE=AG,理由是:(1分)
∵AF⊥BE,
∴∠AFE=∠OAG+AEF=90°,
∵四边形ABCD是正方形,
∴AC⊥BD,AO=BO,
∴∠AOG=∠OAG+∠AGO=90°,
∴∠AEF=∠AGO,(3分)
在△AOG和△BOE中
∵
∴△AOG≌△BOE(AAS),
∴AG=BE;(5分)
(2)∵△AOB是等腰直角三角形,且AB=3,
∴BO=3,
∵OE=1,
∴AE=3+1=4,
由勾股定理得:BE==,
S△ABE=BE?AF=AE?OB,
∴××,
AF=.(8分)
【点评】本题考查了正方形的性质、全等三角形的性质和判定,熟知正方形的四条边都相等,四个角都是直角,对角线互相垂直且相等平分,掌握相关的判定定理和性质定理是解题的关键.
24.如图,正方形ABCD中,AB=4,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE、EF为邻边作矩形DEFG,连接AG.
(1)求证:矩形DEFG是正方形;
(2)求AG+AE的值;
(3)若F恰为AB中点,连接DF交AC于点M,请直接写出ME的长.
【分析】(1)如图,作EM⊥AD于M,EN⊥AB于N.只要证明△EMD≌△ENF即可解决问题;
(2)只要证明△ADG≌△CDE,可得AG=EC即可解决问题;
(3)如图,作EH⊥DF于H.想办法求出EH,HM即可解决问题;
【解答】解:(1)如图,作EM⊥AD于M,EN⊥AB于N.
∵四边形ABCD是正方形,
∴∠EAD=∠EAB,
∵EM⊥AD于M,EN⊥AB于N,
∴EM=EN,
∵∠EMA=∠ENA=∠DAB=90°,
∴四边形ANEM是矩形,
∴∠MEN=∠DEF=90°,
∴∠DEM=∠FEN,
∵∠EMD=∠ENF=90°,
∴△EMD≌△ENF,
∴ED=EF,
∵四边形DEFG是矩形,
∴四边形DEFG是正方形.
(2)∵四边形DEFG是正方形,四边形ABCD是正方形,
∴DG=DE,DC=DA=AB=4,∠GDE=∠ADC=90°,
∴∠ADG=∠CDE,
∴△ADG≌△CDE,
∴AG=CE,
∴AE+AG=AE+EC=AC=AD=4.
(3)如图,作EH⊥DF于H.
∵四边形ABCD是正方形,
∴AB=AD=4,AB∥CD,
∵F是AB中点,
∴AF=FB2
∴DF==2,
∵△DEF是等腰直角三角形,EH⊥AD,
∴DH=HF,
∴EH=DF=,
∵AF∥CD,
∴AF:CD=FM:MD=1:2,
∴FM=,
∴HM=HF﹣FM=,
在Rt△EHM中,EM==.
【点评】本题考查正方形的性质、全等三角形的判定和性质、矩形的性质和判定、解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
25.如图,在正方形ABCD的外侧,作等边三角形BCE,连接AE,DE.
(1)求证:AE=DE
(2)过点D作DF⊥AE,垂足为F,若AB=2cm,求DF的长.
【分析】(1)证明△ABE≌△DCE,可得结论;
(2)作辅助线,构建直角三角形,根据等腰三角形的性质得∠BCG=30°,∠DEF=30°,利用正方形的边长计算DE的长,从而得DF的长.
【解答】(1)证明:∵四边形ABCD是正方形,(1分)
∴AB=CD,∠ABC=∠DCB=90°,
∵△BCE是等边三角形,
∴BE=CE,∠EBC=∠ECB=60°,(2分)
即∠ABE=∠DCE=150°,(3分)
∴△ABE≌△DCE,
∴AE=DE;(5分)
(2)解:过点E作EG⊥CD于G,(6分)
∵DC=CE,∠DCE=150°,
∴∠CDE=∠CED=15°,
∴∠ECG=30°,(7分)
∵CB=CD=AB=2,
∴EG=1,CG=,(8分)
在Rt△DGE中,DE===+,(9分)
在Rt△DEF中,∠EDA=∠DAE=90°﹣15°=75°
∴∠DEF=30°,
∴DF=DE=(cm).(10分)
【点评】本题考查了正方形的性质、等边三角形的性质、全等三角形的判定和性质、等腰三角形的判定和性质,题目的综合性很好,难度不大.
26.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=CD,求证:∠AEF=90°.
【分析】设正方形的边长为4a,先依据勾股定理求得AE、AF、EF的长,然后依据勾股定理的逆定理可证明△AEF为直角三角形.
【解答】证明:∵ABCD为正方形,
∴AB=BC=CD=DA,∠B=∠C=∠D=90°.
设AB=BC=CD=DA=4a,
∵E是BC的中点,且CF=CD,
∴BE=EC=2a,CF=a,
在Rt△ABE中,由勾股定理可得AE2=AB2+BE2=20a2,
同理可得:EF2=EC2+FC2=5a2,AF2=AD2+DF2=25a2,
∵AE2+EF2=AF2,
∴△AEF为直角三角形,
∴∠AEF=90°.
【点评】本题主要考查的是勾股定理和勾股定理的逆定理的定义,熟练掌握勾股定理的逆定理是解题的关键.
27.如图①,正方形ABCD中,点E、F都在AD边上,且AE=FD,分别连接BE、FC,对角线BD交FC于点P,连接AP,交BE于点G;
(1)试判断AP与BE的位置关系;
(2)如图②,再过点P作PH⊥AP,交BC于点H,连接AH,分别交BE、BD于点N,M,请直接写出图②中有哪些等腰三角形.
【分析】(1)由题意可证△ADP≌△DPC,△AEB≌△DFC可得∠DAP=∠DCF=∠ABE,通过角的换算可证AP⊥BE.
(2)根据正方形的性质可得△ABD,△BCD是等腰△,由AP⊥PH,∠ABC=90°可得A,B,H,P四点共圆,可证△APH,△PHC是等腰△
【解答】解:(1)垂直,
理由是∵四边形ABCD是正方形,
∴AD=CD=AB,∠BAD=∠CDA=90°,∠ADB=∠CDB=45°,且DP=DP,
∴△ADP≌△CDP,
∴∠DCF=∠DAP,AP=PC
又AE=DF,∠BAD=∠CDA=90°,AB=CD,
∴△ABE≌△DCF,
∴∠ABE=∠DCF,
∴∠ABE=∠DAP
∵∠ABE+∠AEB=90°,
∴∠DAP+∠AEB=90°,即∠AGE=90°,
∴AP⊥BE
(2)∵AB=BC=CD=DA
∴△ABD,△BCD是等腰△
∵AP⊥PH,∠ABC=90°
∴A,B,H,P四点共圆
∴∠PAH=∠DBC=45°
∴∠PAH=∠PHA=45°
∴PA=PH
∴△APH是等腰△
∵AP=PH,AP=PC,
∴PC=PH
∴△PHC 是等腰△
【点评】本题考查了正方形的性质,全等三角形的性质和判定,关键是利用这些性质解决问题.
28.如图,正方形ABCD中,点E是BC延长线上一点,连接DE,过点B作BF⊥DE于点F,连接FC.
(1)求证:∠FBC=∠CDF;
(2)作点C关于直线DE的对称点G,连接CG,FG,猜想线段DF,BF,CG之间的数量关系,并证明你的结论.
【分析】(1)由题意可得到∠FBC+∠E=90°,∠CDF+∠E=90°,然后依据余角的性质求解即可;
(2)在线段FB上截取FM,使得FM=FD,然后可证明△BDM∽△CDF,由相似三角形的性质可得到BM=FC,然后证明△CFG为等腰直角三角形,从而可得到CG=CF,然后可得到问题的答案.
【解答】解:(1)∵ABCD为正方形,
∴∠DCE=90°.
∴∠CDF+∠E=90°,
又∵BF⊥DE,
∴∠FBC+∠E=90°,
∴∠FBC=∠CDF
(2)如图所示:在线段FB上截取FM,使得FM=FD.
∵∠BDC=∠MDF=45°,
∴∠BDM=∠CDF,
∵==,
∴△BDM∽△CDF,
∴==,∠DBM=∠DCF,
∴BM=CF,
∴∠CFE=∠FCD+∠CDF=∠DBM+∠BDM=∠DMF=45°,
∴∠EFG=∠EFC=45°,
∴∠CFG=90°,
∵CF=FG,
∴CG=CF,
∴BM=CG,
∴BF=BM+FM=CG+DF.
【点评】本题考查四边形综合题、正方形的性质、等腰直角三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题.
29.(1)如图,已知等边△ABC的边长为10,点E是AB上一点,过点E作ED⊥AC于点D,过点D作DF⊥BC于点F.
①若AE=7,求BF的长;
②连接EF,若EF⊥AB,求AE的长;
(2)已知正方形ABCD的边长为10,点E是边AB上一点,过点E作∠AEF=60°交边AD于点F,再过点F作∠DFG=60°交边CD于点G,继续过点G作∠CGH=60°交边BC于点H,连接EH,若∠BHE=60°,请直接写出AE的长.
【分析】(1)①根据直角三角形中,30°所对的直角边是斜边的一半,可依次求AD,FC的长,则BF的长可求
②先证△EDF是等边三角形,再证△ADE≌△BEF≌△DFC,可得AE=BF=CD,BE=CF=AD,即可求AE的长
(2)先证EFGH是矩形,可得EF=HG,EH=FG,根据三角函数可求AF=AE,BE=BH,即可求AE的长度.
【解答】解:(1)①∵△ABC是等边三角形
∴AB=AC=BC=10,∠A=60°=∠B=∠C且DE⊥AC,DF⊥BC
∴∠AED=∠FDC=30°
∵AE=7,DE⊥AC,∠EAD=30°
∴AD=,
∴CD= 且DF⊥BC,∠CDF=30°
∴CF=
∴BF=
②如图1连接EF
∵EF⊥AB,ED⊥AC,DF⊥BC,∠A=∠B=∠C=60°
∴∠AED=∠CDF=∠EFB=30°,
∴∠EDF=∠DFE=∠DEF=60°
∴△DEF是等边三角形,
∴DE=DF=EF且∠A=∠B=∠C,∠AED=∠CDF=∠EFB=30°
∴△ADE≌△BEF≌△DCF
∴AD=CF=BE,AE=BF=CD
∵∠EFB=30°,EF⊥AB
∴BF=2BE即AE=2BE
∵AE+BE=10
∴BE=,AE=
(2)
∵ABCD为正方形
∴∠A=∠B=∠C=∠D=90°,AB=AD=CD=BC
∵∠AEF=∠DFG=∠HGC=∠EHB=60°
∴∠GHC=∠BEH=∠AFE=∠FGD=30°,BE=BH,AF=AE
∴∠FEH=∠EHG=∠HGF=∠EFG=90°
∴EFGH是矩形
∴EH=FG,EF=HG,
∵∠A=∠C=90°,EF=HG,∠AEF=∠HGC=60°
∴△AEF≌△HGC
∴AE=CG,AF=CH同理可得AF=CH
设AE=a,∴AF=a,∴
∴BH=10﹣a,
∵BE=BH=10﹣3a,
∵AE+BE=10
∴10a﹣3a+a=10
∴a=5﹣5
∴AE=5﹣5
【点评】本题考查了等边三角形的性质和判定,正方形的性质,锐角三角函数,关键是灵活运用这些性质解决问题.
30.如图,以△ABC的各边为边长,在边BC的同侧分别作正方形ABDI,正方形BCFE,正方形ACHG,连接AD,DE,EG.
(1)求证:△BDE≌△BAC;
(2)①设∠BAC=α,请用含α的代数式表示∠EDA,∠DAG;
②求证:四边形ADEG是平行四边形;
(3)当△ABC满足什么条件时,四边形ADEG是正方形?请说明理由.
【分析】(1)根据全等三角形的判定定理SAS证得△BDE≌△BAC,
(2)由△BDE≌△BAC,可得全等三角形的对应边DE=AG.然后利用正方形对角线的性质、周角的定义推知∠EDA+∠DAG=180°,易证ED∥GA;最后由“一组对边平行且相等”的判定定理证得结论;
(3)由“正方形的内角都是直角,四条边都相等”易证∠DAG=90°,且AG=AD.由?ABDI和?ACHG的性质证得,AC=AB.
【解答】(1)证明:∵四边形ABDI、四边形BCFE、四边形ACHG都是正方形,
∴AC=AG,AB=BD,BC=BE,∠GAC=∠EBC=∠DBA=90°.
∴∠ABC=∠EBD(同为∠EBA的余角).
在△BDE和△BAC中,
,
∴△BDE≌△BAC(SAS),
(2)①解:∵△BDE≌△BAC,∠ADB=45°,
∴∠EDA=α﹣45°,
∵∠DAG=360°﹣45°﹣90°﹣α=225°﹣α,
②证明:∵△BDE≌△BAC,
∴DE=AC=AG,∠BAC=∠BDE.
∵AD是正方形ABDI的对角线,
∴∠BDA=∠BAD=45°.
∵∠EDA=∠BDE﹣∠BDA=∠BDE﹣45°,
∠DAG=360°﹣∠GAC﹣∠BAC﹣∠BAD
=360°﹣90°﹣∠BAC﹣45°
=225°﹣∠BAC
∴∠EDA+∠DAG=∠BDE﹣45°+225°﹣∠BAC=180°
∴DE∥AG,
∴四边形ADEG是平行四边形(一组对边平行且相等).
(3)解:结论:当四边形ADEG是正方形时,∠DAG=90°,且AG=AD.
理由:由①知,当∠DAG=90°时,∠BAC=135°.
∵四边形ABDI是正方形,
∴AD=AB.
又∵四边形ACHG是正方形,
∴AC=AG,
∴AC=AB.
∴当∠BAC=135°且AC=AB时,四边形ADEG是正方形.
【点评】本题综合考查了正方形的判定与性质,全等三角形的判定与性质,平行四边形的判定与性质等知识点.解题时,注意利用隐含在题干中的已知条件:周角是360°.
31.在△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG,DF.
(1)求证:BD=DF;
(2)求证:四边形BDFG为菱形;
(3)若AG=5,CF=,求四边形BDFG的周长.
【分析】(1)利用平行线的性质得到∠CFA=90°,再利用直角三角形斜边上的中线等于斜边的一半即可得证,
(2)利用平行四边形的判定定理判定四边形BDFG为平行四边形,再利用(1)得结论即可得证,
(3)设GF=x,则AF=5﹣x,利用菱形的性质和勾股定理得到CF、AF和AC之间的关系,解出x即可.
【解答】(1)证明:∵AG∥BD,CF⊥BD,
∴CF⊥AG,
又∵D为AC的中点,
∴DF=AC,
又∵BD=AC,
∴BD=DF,
(2)证明:∵BD∥GF,BD=FG,
∴四边形BDFG为平行四边形,
又∵BD=DF,
∴四边形BDFG为菱形,
(3)解:设GF=x,则AF=5﹣x,AC=2x,
在Rt△AFC中,(2x)2=+(5﹣x)2,
解得:x1=2,x2=﹣(舍去),
∴GF=2,
∴菱形BDFG的周长为8.
【点评】本题考查了菱形的判定与性质直角三角形斜边上的中线,勾股定理等知识,正确掌握这些定义性质及判定并结合图形作答是解决本题的关键.
32.如图,长方形ABCD在平面直角坐标系中,已知点A(0,a),B(0,6),C(b,6),且满足a=+8.
(1)请直接写出A、C、D三个点的坐标,A (0,8) ,C (4,6) ,D (4,8) ;
(2)连接线段BD、OD,试求三角形BOD的面积;
(3)若长方形ABCD以每秒1个单位长度匀速向下运动,设运动的时间为t秒,问是否存在某一时刻,三角形BOD的面积与长方形ABCD的面积相等?若存在,请求出t的值;若不存在,请说明理由.
【分析】(1)利用二次根式的性质求出a、b的值即可解决问题;
(2)根据三角形的面积公式计算即可;
(3)分两种情形分别计算即可;
【解答】解:(1)∵a=+8,
又∵,
∴b=4,a=8,
∴A(0,8),C(4,6),D(4,8),
故答案为(0,8),(4,6),(4,8);
(2)由题意:S△OBD=×6×4=12.
(3)存在.
理由:当长方形ABCD在x轴的上方时,BO=6﹣t,则×4×(6﹣t)=2×4,
解得t=2,
当长方形ABCD在x轴的下方时,BO=t﹣6,
则×4(t﹣6)=2×4,
解得t=10,
答:运动的时间2或10秒时,三角形BOD的面积与长方形ABCD的面积相等.
【点评】本题考查矩形的性质、坐标与图形的性质、二次根式的性质、三角形的面积等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
33.已知:如图,菱形ABCD的对角线AC,BD相交于O,点E,F分别是AD,DC的中点,已知OE=,EF=3,求菱形ABCD的周长和面积.
【分析】首先由菱形ABCD的对角线AC,BD相交于O,点E,F分别是AD,DC的中点,根据直角三角形斜边上的中线等于斜边的一半,可求得AB的长,由三角形中位线定理可求得AC的长,进而可求出菱形的周长,再求出AC的长即可求出菱形的面积.
【解答】解:∵菱形ABCD的对角线AC,BD相交于点O,
∴AC⊥BD,OA=OC,OB=OD,
∵点E,F分别是AD,DC的中点,
∴OE=AB,EF=AC,
∵OE=2.5,EF=3,
∴AB=5,AC=6,
∴菱形ABCD的周长为:4×5=20;
∵AO=AC=3,AB=5,
∴BO==4,
∴BD=2BO=8,
∴菱形ABCD的面积=AC?BD=24.
【点评】此题考查了菱形的性质、三角形中位线的性质、勾股定理以及直角三角形的性质.注意根据题意求得AC与AB的长是解此题的关键.
34.如图,在△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:四边形BDFG是菱形;
(2)若AG=11,CF=8,求四边形BDFG的周长.
【分析】(1)首先可判断四边形BGFD是平行四边形,再由直角三角形斜边中线等于斜边一半,可得BD=FD,则可判断四边形BGFD是菱形;
(2)设GF=x,则AC=2x,AF=11﹣x.在Rt△ACF中,依据勾股定理方程求解即可.
【解答】解:∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CF⊥BD,
∴CF⊥AG,
又∵点D是AC中点,
∴BD=DF=AC,
∴四边形BGFD是菱形.
(2)设GF=x,则DF=x,AC=2x.
∵AF=AG﹣GF,
∴AF=11﹣x.
在Rt△ACF中,∠AFC=90°.
∴AF2+CF2=AC2,
∴(11﹣x)2+82=(2x)2,
解得:x=5(负值已舍去).
∴FG=5.
∴菱形BDFG的周长=4GF=20.
【点评】本题考查了菱形的判定与性质、勾股定理及直角三角形的斜边中线的性质,解答本题的关键是依据题意列出关于x的方程.
35.如图,在△ABC中,AD、BE分别是边BC、AC上的中线,AD与BE交于点O,点F、G分别是BO、AO的中点,联结DE、EG、GF、FD.
(1)求证:FG∥DE;
(2)若AC=BC,求证:四边形EDFG是矩形.
【分析】(1)依据三角形的中位线定理可得到DE∥AB且DE=AB、FG∥AB且FG=AB,从而可证明FG∥DE;
(2)首先证明四边形EDFG是平行四边形,然后再证明EF=DG,最后,依据矩形的判定定理进行证明即可.
【解答】解:(1)∵AD、BE分别是边BC、AC上的中线,
∴DE是△ABC的中位线,
∴DE∥AB且DE=AB.
∵点F、G分别是BO、AO的中点,
∴FG是△OAB的中位线,
∴FG∥AB且FG=AB.
∴GF∥DE.
(2)由(1)GF∥DE,GF=DE
∴四边形EDFG是平行四边形.
∵AD、BE是BC、AC上的中线,
∴CD=BC,CE=AC.
又∵AC=BC,
∴CD=CE.
在△ACD和△BCE中,,
∴△ACD≌△BCE,
∴∠CAB=∠CBA.
∵AC=BC,
∴∠CAB=∠CBA,
∴∠DAB=∠EBA,
∴OB=OA.
∵点F、G分别是OB、AO的中点,
∴OF=OB,OG=OA,
∴OF=OG,
∴EF=DG,
∴四边形EDFG是矩形.
【点评】本题主要考查的是矩形的判定、三角形的中位线定理,熟练掌握三角形的中位线定理是解题的关键.
36.(1)如图(1),已知:正方形ABCD的对角线交于点O,E是AC上的一动点,过点A作AG⊥BE于G,交BD于F.求证:OE=OF.
(2)在(1)的条件下,若E点在AC的延长线上,以上结论是否成立,为什么?
【分析】(1)利用正方形的性质得OA=OB,∠AOB=∠BOC=90°,则利用等角的余角相等得到∠GAE=∠OBE,则可根据”ASA“判断△AOF≌△BOE,从而得到OF=OE;
(2)同样方法证明△AOF≌△BOE,仍然得到OF=OE.
【解答】(1)证明:∵四边形ABCD为正方形,
∴OA=OB,∠AOB=∠BOC=90°,
∵AG⊥BE于点G,
∴∠AGE=90°,
∴∠GAE=∠OBE,
在△AOF和△BOE中
,
∴△AOF≌△BOE(ASA),
∴OF=OE;
(2)解:以上结论仍然成立.理由如下:
同样可证明△AOF≌△BOE(ASA),所以OF=OE.
【点评】本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质;两条对角线将正方形分成四个全等的等腰直角三角形,同时,正方形又是轴对称图形,有四条对称轴.
37.如图,已知点P为∠ACB平分线上的一点,∠ACB=60°,PD⊥CA于D,PE⊥CB于E.点M是线段CP上的动点(不与两端点C、P重合),连接DM,EM.
(1)求证:DM=ME;
(2)当点M运动到线段CP的什么位置时,四边形PDME为菱形,请说明理由.
【分析】(1)先利用角平分线定义得到∠ACP=∠BCP=30°,再根据角平分线的性质得PD=PE,则利用“HL”可证明Rt△DCP≌Rt△ECP得到CD=CE,然后证明△DCM≌△ECM得到DM=ME;
(2)利用∠DCP=30°得到PC=2PD,∠CPD=60°,则当DM=DP时,PD=PE=MD=ME,则四边形DMEP为菱形,由于此时△PDM为等边三角形,所以PD=PM,从而得到CM=PM,即当点M运动到线段CP的中点时,四边形PDME为菱形.
【解答】(1)证明:∵点P为∠ACB平分线上的一点,
∴∠ACP=∠BCP=30°,
∵PD⊥CA于D,PE⊥CB于E,
∴PD=PE,
在Rt△DCP和Rt△ECP中
,
∴Rt△DCP≌Rt△ECP,
∴CD=CE,
在△DCM和△ECM中
,
∴△DCM≌△ECM,
∴DM=ME;
(2)解:当点M运动到线段CP的中点时,四边形PDME为菱形.
理由如下:∵∠DCP=30°,
∴PC=2PD,∠CPD=60°,
∵PD=PE,MD=ME,
∴当DM=DP时,PD=PE=MD=ME,则四边形DMEP为菱形,
此时△PDM为等边三角形,
∴PD=PM,
∴CM=PM,
∴当点M运动到线段CP的中点时,四边形PDME为菱形.
【点评】本题考查了菱形的判定:一组邻边相等的平行四边形是菱形(平行四边形+一组邻边相等=菱形);四条边都相等的四边形是菱形.也考查了全等三角形的判定与性质和角平分线的性质.
38.如图,正方形ABCD的边长为2,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F.
(1)求证:AF=BE;
(2)求点E到BC边的距离.
【分析】(1)利用正方形的性质得OA=OB,∠AOB=∠BOC=90°,再利用等角的余角相等得到∠MAE=∠OBE,则利用”ASA“可判断△AOF≌△BOE,然后根据全等三角形的性质得到结论;
(2)作EN⊥BC于N,如图,由正方形的性质得OC=BC=2,∠OCB=45°,则CE=1,然后利用△CEN为等腰直角三角形即可得到EN=CE=.
【解答】(1)证明:∵四边形ABCD为正方形,
∴OA=OB,∠AOB=∠BOC=90°,
∵AM⊥BE于点M,
∴∠AME=90°,
∴∠MAE=∠OBE,
在△AOF和△BOE中
,
∴△AOF≌△BOE(ASA),
∴AF=BE;
(2)解:作EN⊥BC于N,如图,
∵四边形ABCD为正方形,
∴OC=BC=×2=2,∠OCB=45°,
∵E是OC的中点,
∴CE=1,
在Rt△ECN中,∵∠ECN=45°,
∵△CEN为等腰直角三角形,
∴EN=CE=,
即点E到BC边的距离为.
【点评】本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质;两条对角线将正方形分成四个全等的等腰直角三角形,同时,正方形又是轴对称图形,有四条对称轴.
39.菱形ABCD中,F是对角线AC的中点,过点A作AE⊥BC垂足为E,G为线段AB上一点,连接GF并延长交直线BC于点H.
(1)当∠CAE=30°时,且CE=,求菱形的面积;
(2)当∠BGF+∠BCF=180°,AE=BE时,求证:BF=(+1)GF.
【分析】(1)只要证明△ABC是等边三角形,即可解决问题;
(2)如图,连接GC,作GM⊥GF交BF于M.想办法证明△BGC是等腰直角三角形,再证明△BGM≌△CGF即可解决问题;
【解答】(1)解:∵四边形ABCD是菱形,
∴AB=BC,
∵AE⊥BC,∠EAC=30°,
∴∠ACE=60°,AC=2EC=2,
∴△ABC,△ACD都是等边三角形,
∴S菱形ABCD=2?S△ABC=2××(2)2=6.
(2)如图,连接GC,作GM⊥GF交BF于M.
∵四边形ABCD是菱形,
∴BA=BC,∵AF=FC,
∴BF⊥AC,
∴∠BFA=90°,
∵∠BGF+∠BCF=180°,∠AGF+∠BGF=180°,
∴∠AGF=∠ACB,∵∠GAF=∠CAB
∴△AGF∽△ACB,
∴=,
∴=,∵∠CAG=∠BAF,
∴△CAG∽△BAF,
∴∠CGA=∠BFA=90°,
∵AE⊥BE,AE=BE,
∴∠ABE=45°,
∴∠GBC=∠GCB=45°,
∴GB=GC,
∵∠BGC=∠MGF,
∴∠BGM=∠CGF,
∵∠GBM=∠GCF,
∴△BGM≌△CGF,
∴BM=CF,GM=GF,FM=GF,
∵∠AGC=90°AF=FC,
∴GF=FC=BM,
∴BF=BM+FM=GF+GF=(+1)GF.
【点评】本题考查菱形的性质、等边三角形的判定和性质、全等三角形的判定和性质、等腰直角三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.
40.如图,P为正方形ABCD边BC上任一点,BG⊥AP于点G,在AP的延长线上取点E,使AG=GE,连接BE、CE,作DM⊥AG于M.
(1)求证:DM=AG;
(2)若△BCE是等边三角形,连DE,△ADE的面积为25,求BG长.
【分析】(1)先证明△ADM≌△BAG,然后依据全等三角形的性质可证明DM=AG.
(2)过点A作AF⊥BE,垂足为F.由(1)可知AG=MD=GE,然后依据三角形ADE的面积为25可求得DM的长,然后再证明∠ABF=30°,设AB=BE=a,则FB=a,EF=(+2)a,在Rt△AFE中,依据勾股定理可得到4a2=100(2﹣),即AB2=100(2﹣),最后,在Rt△ABG中,依据勾股定理求解即可.
【解答】解:(1)∵DM⊥AG,BG⊥AP,
∴∠AMD=∠AGB=90°.
∵∠DAM+∠GAB=90°,∠DAM+∠ADM=90°,
∴∠GAB=∠ADM.
在△ADM和△BAG中,∠AMD=∠AGB=90°,∠GAB=∠ADM,AB=AD,
∴△ADM≌△BAG.
∴DM=AG.
(2)如图所示:过点A作AF⊥BE,垂足为F.
∵△BCE是等边三角形,ABCD为正方形,
∴AB=EB,∠ABE=150°.
∴∠ABE=30°.
∴AF=AB.
设AB=BE=a,则FB=a,AB=2a,EF=(+2)a.
∵AG=GE=MD,△ADE的面积为25,
∴MD?AE=MD?2MD=25,解得MD=5.
∴AE=10.
在Rt△AFE中,AE2=AF2+EF2,即[(+2)a]2+a2=102,解得:4a2=100(2﹣).
∴AB2=100(2﹣).
∴BG====5=5=5×(2﹣)=10﹣5.
【点评】本题主要考查的是正方形的性质、等边三角形的性质、勾股定理的应用、含30°直角三角形的性质,熟练掌握相关图形的性质是解题的关键.
41.如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD,BE,BC于点P,O,Q,连接BP,EQ.
(1)求证:四边形BPEQ是菱形;
(2)F为AB的中点,则线段OF与线段AE有什么位置关系和数量关系?直接写出结论,不必证明.
(3)在(2)的条件下,若AB=6,OF=4,求PQ的长.
【分析】(1)先根据线段垂直平分线的性质证明PB=PE,由ASA证明△BOQ≌△EOP,得出PE=QB,证出四边形ABGE是平行四边形,再根据菱形的判定即可得出结论;
(2)先证明OF为△BAE的中位线,然后依据三角形的中位线定理进行解答即可;
(3)先求得OB的长,则可得到BE的长,设菱形的边长为x,则AP=8﹣x,在Rt△APB中依据勾股定理可列出关于x的方程,然后依据菱形的面积公式可求得PQ的长.
【解答】解:(1)证明:∵PQ垂直平分BE,
∴PB=PE,OB=OE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PEO=∠QBO,
在△BOQ与△EOP中,∠PEO=∠QBO,OB=OE,∠POE=∠QOB,
∴△BOQ≌△EOP(ASA),
∴PE=QB,
又∵AD∥BC,
∴四边形BPEQ是平行四边形,
又∵QB=QE,
∴四边形BPEQ是菱形;
(2)∵四边形BPEQ是菱形,
∴OB=OE.
又∵F是AB的中点,
∴OF是△BAE的中位线,
∴AE∥OF且OF=AE.
(3)∵AB=6,F是AB的中点,
∴BF=3.
∵OF∥AE,
∴∠BFO=90°.
在Rt△FOB中,OB==5.
∴BE=10.
设菱形的边长为x,则AP=8﹣x.
在Rt△APB中,BP2=AB2+AP2,即x2=62+(8﹣x)2,解得:x=.
由菱形的面积公式可知:×6=×10PQ,解得:PQ=.
【点评】本题考查了菱形的判定与性质、矩形的性质,平行四边形的判定与性质、线段垂直平分线的性质、勾股定理等知识,列出关于x的方程是解题的关键.
42.如图,在△ABC中,BD、CE分别为AC、AB边上的中线,BD、CE交于点H,点G、F分别为HC、HB的中点,连接AH、DE、EF、FG、GD,其中HA=BC.
(1)证明:四边形DEFG为菱形;
(2)猜想当AC、AB满足怎样的数量关系时,四边形DEFG为正方形,并说明理由.
【分析】(1)利用三角形中位线定理推知ED∥FG,ED=FG,则由“对边平行且相等的四边形是平行四边形”证得四边形DEFG是平行四边形,同理得EF=HA=BC=DE,可得结论;
(2)AC=AB时,四边形DEFG为正方形,通过证明△DCB≌△EBC(SAS),得HC=HB,证明对角线DF=EG,可得结论.
【解答】(1)证明:∵D、E分别为AC、AB的中点,
∴ED∥BC,ED=BC.
同理FG∥BC,FG=BC,
∴ED∥FG,ED=FG,
∴四边形DEFG是平行四边形,
∵AE=BE,FH=BF,
∴EF=HA,
∵BC=HA,
∴EF=BC=DE,
∴?DEFG是菱形;
(2)解:猜想:AC=AB时,四边形DEFG为正方形,
理由是:∵AB=AC,
∴∠ACB=∠ABC,
∵BD、CE分别为AC、AB边上的中线,
∴CD=AC,BE=AB,
∴CD=BE,
在△DCB和△EBC中,
∵,
∴△DCB≌△EBC(SAS),
∴∠DBC=∠ECB,
∴HC=HB,
∵点G、F分别为HC、HB的中点,
∴HG=HC,HF=HB,
∴GH=HF,
由(1)知:四边形DEFG是菱形,
∴DF=2FH,EG=2GH,
∴DF=EG,
∴四边形DEFG为正方形.
【点评】本题考查了平行四边形、矩形的判定、菱形的判定、正方形的判定、三角形的中位线性质定理,三角形中线的性质及等腰三角形的性质,其中三角形的中位线的性质定理为证明线段相等和平行提供了依据.
43.在菱形ABCD中,AC是对角线,CD=CE,连接DE,点M是线段DE的中点.
(1)如图1,连接CM,若AC=16,CD=10,求DE的长;
(2)如图2,点F在菱形的外部,DF=DM,且∠CDA=∠FDE,连接FM交AD于点G,FM的延长线交AC于点N,求证:CN=AG.
【分析】(1)过D作DP⊥AC交AC于P.想办法求出PE,DP的值即可解决问题;
(2)连接AF,CM.想办法证明△AFD≌△CME,△AFG≌△MNC即可解决问题;
【解答】解:(1)过D作DP⊥AC交AC于P.
∵DC=AD,DP⊥AC
∴CP=AC=8
又∵DC=10
∴DP=6
∵EC=DC=10
∴AE=6
∴EP=2,DE==2.
(2)连接AF,CM.
∵CD=CE
∴∠CDE=∠CED
又∵∠CDA=∠FDE
∴∠FDA=∠CDE=∠CED
在△AFD和△CME中
,
∴△AFD≌△CME
∴∠FAD=∠MCE AF=CM
又∵FD=DM
∴∠DFM=∠DMF=∠EMN
∵∠AFD=∠EMC∠AFG+∠DFM=∠CMN+∠EMN
∴∠AFG=∠CMN
∴在△AFG和△MNC中
,
∴△AFG≌△MNC
∴CN=AG.
【点评】本题考查菱形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
44.在菱形ABCD中,∠C=60°,E为CD边上的点,连接BE.
(1)如图1,若E为CD的中点且BE=3,求菱形ABCD的面积.
(2)如图2,点F在BC边上,且DE=CF,连接DF交BE于点M,连接EB并延长至点N,使得BN=DM,求证:AN=DM+BM.
【分析】(1)只要证明△BDC是等边三角形,求出CD即可解决问题;
(2)如图2中,连接AM,在MA上截取MH=MD,连接DH.想办法证明△AMN,△DMH都是等边三角形,△ADH≌△BDM即可解决问题;
【解答】解:(1)如图1中,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵∠C=60°,
∴△BCD是等边三角形,
∵DE=EC,
∴BE⊥CD,
∴tan60°=,
∴EC=,
∴CD=2EC=2,
∴菱形ABCD的面积=CD?BE=6.
(2)如图2中,连接AM,在MA上截取MH=MD,连接DH.
∵DE=CF.∠BDE=∠C,BD=CD,
∴△BDE≌△DCF,
∴∠DBE=∠CDF,
∴∠MBF=∠DBM+∠BDM=∠CDF+∠BDM=60°,
∴∠DMB=120°,
∵∠DAB+∠DMB=180°,
∴∠ADM+∠ABM=180°,
∵∠ABN+∠ABM=180°,
∴∠ABN=∠ADM,
∵AB=AD,BN=DM,
∴△ABN≌△ADM,
∴∠DAM=∠BAN,AM=AN,
∴∠MAN=∠DAB=60°,
∴△AMN是等边三角形,
∴∠AMB=∠AMD=60°,
∵MH=MD,
∴△DMN是等边三角形,
∴DH=DM,∠ADB=∠HDM=60°,
∴∠ADH=∠BDM,
∵AD=DB,DH=DM.
∴△ADH≌△BDM,
∴AH=BM,
∵AM=AH+HM,
∴AN=AM=DM+BM.
【点评】本题考查菱形的性质、等边三角形的判定和性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.
45.正方形ABCD中,点P是边CD上的任意一点,连接BP,O为BP的中点,作PE⊥BD于E,连接EO,AE.
(1)若∠PBC=α,求∠POE的大小(用含α的式子表示);
(2)用等式表示线段AE与BP之间的数量关系,并证明.
【分析】(1)先根据正方形的性质得:∠DBC=∠CDB=45°,则∠DBP=45°﹣α,根据直角三角形斜边中线的性质可得EO=BO,由等腰三角形性质和外角的性质可得结论;
(2)作辅助线,证明△ABE≌△CBE,则AE=CE,根据直角三角形斜边中线的性质得:OC=OB=OP=OE,证明△EOC是等腰直角三角形,最后由勾股定理可得:BP=,所以BP=.
【解答】解:(1)在正方形ABCD中,BC=DC,∠C=90°,
∴∠DBC=∠CDB=45°,
∵∠PBC=α,
∴∠DBP=45°﹣α,……………………………………(1分)
∵PE⊥BD,且O为BP的中点,
∴EO=BO,……………………………………(2分)
∴∠EBO=∠BEO,
∴∠EOP=∠EBO+∠BEO=90°﹣2 α;……………………………………(3分)
(2)连接OC,EC,
在正方形ABCD中,AB=BC,∠ABD=∠CBD,BE=BE,
∴△ABE≌△CBE,
∴AE=CE,……………………………………(4分)
在Rt△BPC中,O为BP的中点,
∴CO=BO=,
∴∠OBC=∠OCB,
∴∠COP=2 α,……………………………………(5分)
由(1)知∠EOP=90°﹣2α,
∴∠EOC=∠COP+∠EOP=90°,
又由(1)知BO=EO,
∴EO=CO.
∴△EOC是等腰直角三角形,……………………………………(6分)
∴EO2+OC2=EC2,
∴EC=OC=,
即BP=,
∴BP=.……………………………………(7分)
【点评】本题考查正方形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质、勾股定理等知识,第(2)问有难度,作辅助线,构建全等三角形和等腰直角三角形是解决问题的关键.
46.边长为a的正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连结CE.
(1)若点F在边BC上(如图);
①求证:CE=EF;
②若BC=2BF,求DE的长.
(2)若点F在CB延长线上,BC=2BF,请直接写出DE的长.
【分析】(1)①先利用正方形的对称性可得到∠BAE=∠BCE,然后在证明又∠BAE=∠EFC,通过等量代换可得到∠BCE=∠EFC;②过点E作MN⊥BC,垂直为N,交AD于M.依据等腰三角形的性质可得到FN=CN,从而可得到NC的长,然后可得到MD的长,在Rt△MDE中可求得ED的长;
(2)先根据题意画出图形,然后再证明EF=EC,然后再按照(1)②中的思路进行证明即可.
【解答】解:(1)①证明:∵正方形ABCD关于BD对称,
∴△ABE≌△CBE,
∴∠BAE=∠BCE.
又∵∠ABC=∠AEF=90°,
∴∠BAE=∠EFC,
∴∠BCE=∠EFC,
∴CE=EF.
②过点E作MN⊥BC,垂直为N,交AD于M.
∵CE=EF,
∴N是CF的中点.
∵BC=2BF,
∴=.
又∵四边形CDMN是矩形,△DME为等腰直角三角形,
∴CN=DM=ME,
∴ED=DM=CN=a.
(2)如图所示:过点E作MN⊥BC,垂直为N,交AD于M.
∵正方形ABCD关于BD对称,
∴△ABE≌△CBE,
∴∠BAE=∠BCE.
又∵∠ABF=∠AEF=90°,
∴∠BAE=∠EFC,
∴∠BCE=∠EFC,
∴CE=EF.
∴FN=CN.
又∵BC=2BF,
∴FC=a,
∴CN=a,
∴EN=BN=a,
∴DE=a.
【点评】本题主要考查的是正方形的性质、全等三角形的性质和判定、等腰三角形的性质和判定、等腰直角三角形的性质,掌握本题的辅助线的法则是解题的关键.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2019/4/20 13:27:10;用户:zhrasce20;邮箱:zhrasce20@163.com;学号:6322261
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
