浙江省东阳市林头中学2018-2019学年八年级下第4章平行四边形单元测试卷(含答案)
文档属性
| 名称 | 浙江省东阳市林头中学2018-2019学年八年级下第4章平行四边形单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 170.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-04-30 09:48:34 | ||
图片预览


文档简介
浙教版八年级下第4章《平行四边形》单元测试
一、选择题:
1、四边形ABCD中,AD∥BC,要判别四边形ABCD是平行四边形,还需满足条件( )
A.∠A+∠C=180° B.∠B+∠D=180°
C.∠A+∠B=180° D.∠A+∠D=180°
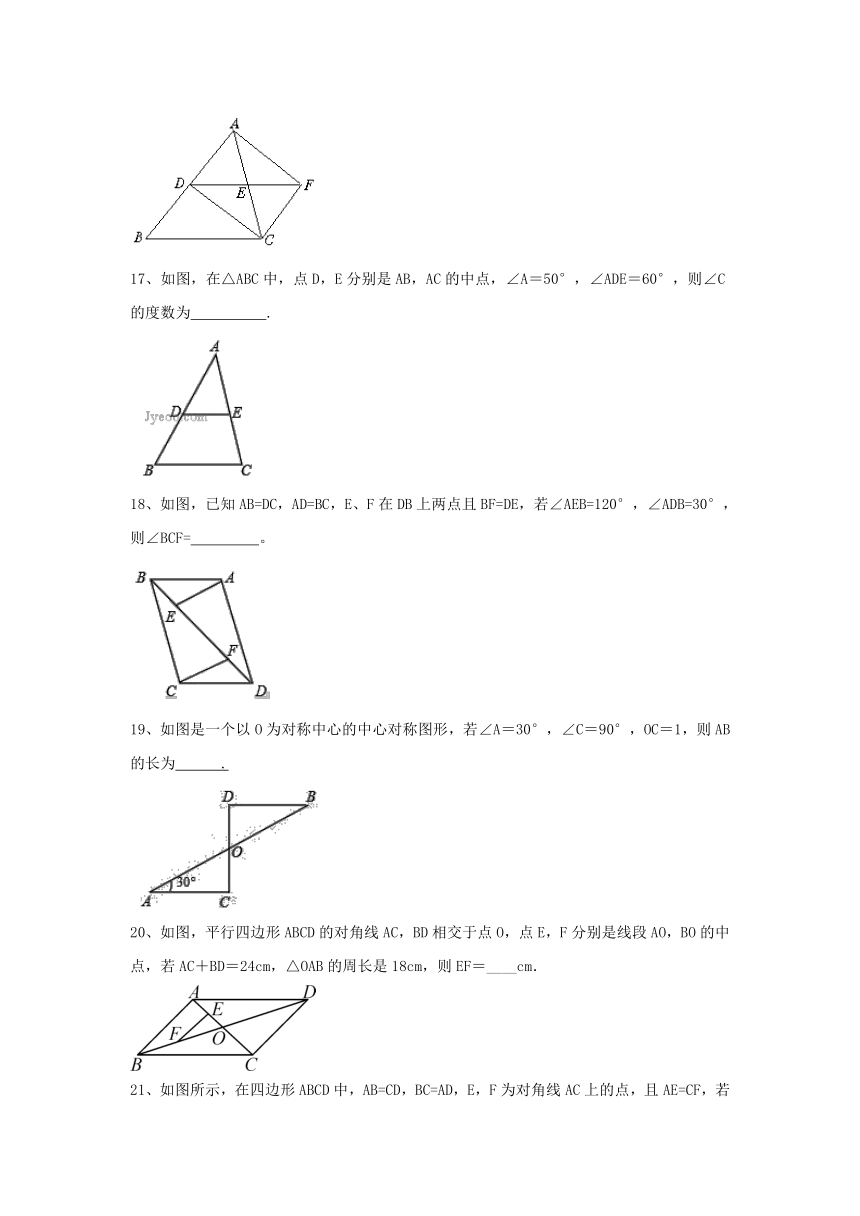
2、下列图形中,是中心对称图形的是( )
3、下列命题中,假命题是( )
A.平行四边形的对角线互相平分; B.矩形的对角线相等
C.等腰梯形的对角线相等; D.菱形的对角线相等且互相平分
4、一个多边形的内角和与外角和相等,则这个多边形是( )
A.三角形 B.四边形 C.五边形 D.都可以
5、选择用反证法证明“已知:在△ABC中,∠C=90°. 求证:∠A,∠B中至少有一个角不大于45°.”时,应先假设( )
A. ∠A>45°,∠B>45° B. ∠A≥45°,∠B≥45°
C. ∠A<45°,∠B<45° D. ∠A≤45°,∠B≤45°
6、如图所示,四边形ABCD的对角线AC和BD相交于点O,下列判断正确的是( ).
A.若AO=OC,则ABCD是平行四边形;
B.若AC=BD,则ABCD是平行四边形;
C.若AO=BO,CO=DO,则ABCD是平行四边形;
D.若AO=OC,BO=OD,则ABCD是平行四边形
7、一个五边形的五个外角的度数比是1∶2∶3∶4∶5,这个五边形的五个内角的度数比( ).
A. 1∶2∶3∶4∶5 B. 5∶4∶3∶2∶1
C. 13∶11∶9∶7∶5 D. 11∶9∶7∶5∶3
8、已知△ABC的各边长度分别为3 cm,4 cm,5 cm,则连结各边中点的三角形的周长为( )
A.2 cm B.7 cm C.5 cm D.6 cm
9、如图,在△ABC中,点D,E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )
A.8 B.10 C.12 D.14
10、已知平行四边形ABCD的周长为32,AB=4,则BC=(??? )
A.?12?????B.?8????C.?24????D.?28
11、如图,点D,E,F分别是△ABC三边上的中点.若△ABC的面积为12 cm2,则△DEF的面积为 ( )
A.3cm2. B.6cm2. C.5cm2. D.4cm2.
12、平行四边形ABCD中,∠ABC的平分线将AD边分成的两部分的长分别为2和3,则平行四边形ABCD的周长是( )
A.8或12 B.10或15 C.14或16 D.14或21
二、填空题:
13、 命题“线段垂直平分线上的点到线段两端的距离相等”的逆命题是_______,这个命题是________命题.(填“真”或“假”)
14、n边形与m边形内角和度数差为720°,则n与m的差为 .
15、如图,直线AB,CD相交,求证:AB,CD只有一个交点.
证明:假设AB,CD相交于两个交点O与O′,那么过O,O′两点就有_____条直线,这与“过两点_______”矛盾,所以假设不成立,则________.
16、如图,DE∥BC,AE=EC,延长DE到F,使EF=DE,连结AF、FC、CD,则图中四边形ADCF是______.
17、如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为 .
18、如图,已知AB=DC,AD=BC,E、F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF= 。
19、如图是一个以O为对称中心的中心对称图形,若∠A=30°,∠C=90°,OC=1,则AB的长为 .
20、如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24cm,△OAB的周长是18cm,则EF=____cm.
21、如图所示,在四边形ABCD中,AB=CD,BC=AD,E,F为对角线AC上的点,且AE=CF,若BE=4,则DF= .
22、如图所示,B、C、E三点在一条直线上,△ABC 和△DCE均为等边三角形,连结AE、DB.若AB=5,AE=12,则DB= .
三、解答题:
23、两个正多边形的边数之比为1∶2,内角和之比为3∶8,求这两个多边形的边数、内角和.
24、如图所示,在四边形ABCD中,DC∥AB,以AD,AC为边作□ACED,延长DC交EB于F,求证:EF=FB.
25、如图,点D,E分别在边AB,AC上,BD=CE,BE,CD的中点分别是M,N,直线MN分别交AB,AC于点P,Q.求证:AP=AQ.
26、如图所示,梯形ABCD中,AD∥BC,F、H分别是AB、CD的中点, FH分别交BD、AC于G、M, BD=6,ED=2,BC=10.
(1)求GM的长;(2)若梯形ABCD是等腰梯形,求证:△BFG≌△CHM.
27、如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)若AB=6,求平行四边形BCFD的面积.
参考答案
一、选择题:
1、D 2、C 3、D 4、B 5、A 6、D
7、C 8、D 9、C 10、A 11、A 12、C
二、填空题:
13、到线段两端距离相等的点在这条线段的垂直平分线上,真.
14、4
15、两;有且只有一条直线;原命题成立
16、平行四边形
17、70°
18、90°
19、4
20、3
21、4
22、12
三、解答题:
23、五边形,540°;十边形,1440°
24、过点B作BG∥AD,交DC的延长线于G,连接EG.
∵DC∥AB,∴ABGD是平行四边形,∴BG AD.
在□ACED中,ADCE,∴CEBG.
∴四边形BCEG为平行四边形,∴EF=FB.
25、取BC的中点K,连结KM,KN,
∴KM,KN分别是△BCE和△BCD的中位线,
∴KM∥AC,KM=CE,KN∥AB,KN=BD,
∴∠AQP=∠KMN,∠APQ=∠KNM,
又∵BD=CE,∴KM=KN,∴∠KMN=∠KNM,
∴∠APQ=∠AQP,∴AP=AQ
26、∵F、H为AB、CD的中点,∴AD∥FH∥BC.
∴△AED∽△CEB.∴,∴.∴AD=5.
又∵△AED∽△MEC,∴.∴,∴MG=.
(2)∵等腰梯形ABCD中F、H分别是AB、CD的中点,
∴BF=CH,∠BAD=∠CDA,FH∥AD.∴∠BFG=∠CHM.
∴FG=HM=AD.∴△BFG≌△CHM.
27、(1)证明:在△ABC中,∠ACB=90°,∠CAB=30°,∴∠ABC=60°.
在等边△ABD中,∠BAD=60°,∴∠BAD=∠ABC=60°.
∵E为AB的中点,∴AE=BE.
又∵∠AEF=∠BEC,∴△AEF≌△BEC.
在△ABC中,∠ACB=90°,E为AB的中点,∴CE=AB,BE=AB.
∴CE=AE,∴∠EAC=∠ECA=30°,∴∠BCE=∠EBC=60°.
又∵△AEF≌△BEC,∴∠AFE=∠BCE=60°.
又∵∠D=60°,∴∠AFE=∠D=60°.∴FC∥BD.
又∵∠BAD=∠ABC=60°,∴AD∥BC,即FD∥BC.
∴四边形BCFD是平行四边形.
(2)解:在Rt△ABC中,∵∠BAC=30°,AB=6,
∴BC=AB=3,AC=BC=3,∴S=3×=9.
一、选择题:
1、四边形ABCD中,AD∥BC,要判别四边形ABCD是平行四边形,还需满足条件( )
A.∠A+∠C=180° B.∠B+∠D=180°
C.∠A+∠B=180° D.∠A+∠D=180°
2、下列图形中,是中心对称图形的是( )
3、下列命题中,假命题是( )
A.平行四边形的对角线互相平分; B.矩形的对角线相等
C.等腰梯形的对角线相等; D.菱形的对角线相等且互相平分
4、一个多边形的内角和与外角和相等,则这个多边形是( )
A.三角形 B.四边形 C.五边形 D.都可以
5、选择用反证法证明“已知:在△ABC中,∠C=90°. 求证:∠A,∠B中至少有一个角不大于45°.”时,应先假设( )
A. ∠A>45°,∠B>45° B. ∠A≥45°,∠B≥45°
C. ∠A<45°,∠B<45° D. ∠A≤45°,∠B≤45°
6、如图所示,四边形ABCD的对角线AC和BD相交于点O,下列判断正确的是( ).
A.若AO=OC,则ABCD是平行四边形;
B.若AC=BD,则ABCD是平行四边形;
C.若AO=BO,CO=DO,则ABCD是平行四边形;
D.若AO=OC,BO=OD,则ABCD是平行四边形
7、一个五边形的五个外角的度数比是1∶2∶3∶4∶5,这个五边形的五个内角的度数比( ).
A. 1∶2∶3∶4∶5 B. 5∶4∶3∶2∶1
C. 13∶11∶9∶7∶5 D. 11∶9∶7∶5∶3
8、已知△ABC的各边长度分别为3 cm,4 cm,5 cm,则连结各边中点的三角形的周长为( )
A.2 cm B.7 cm C.5 cm D.6 cm
9、如图,在△ABC中,点D,E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )
A.8 B.10 C.12 D.14
10、已知平行四边形ABCD的周长为32,AB=4,则BC=(??? )
A.?12?????B.?8????C.?24????D.?28
11、如图,点D,E,F分别是△ABC三边上的中点.若△ABC的面积为12 cm2,则△DEF的面积为 ( )
A.3cm2. B.6cm2. C.5cm2. D.4cm2.
12、平行四边形ABCD中,∠ABC的平分线将AD边分成的两部分的长分别为2和3,则平行四边形ABCD的周长是( )
A.8或12 B.10或15 C.14或16 D.14或21
二、填空题:
13、 命题“线段垂直平分线上的点到线段两端的距离相等”的逆命题是_______,这个命题是________命题.(填“真”或“假”)
14、n边形与m边形内角和度数差为720°,则n与m的差为 .
15、如图,直线AB,CD相交,求证:AB,CD只有一个交点.
证明:假设AB,CD相交于两个交点O与O′,那么过O,O′两点就有_____条直线,这与“过两点_______”矛盾,所以假设不成立,则________.
16、如图,DE∥BC,AE=EC,延长DE到F,使EF=DE,连结AF、FC、CD,则图中四边形ADCF是______.
17、如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为 .
18、如图,已知AB=DC,AD=BC,E、F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF= 。
19、如图是一个以O为对称中心的中心对称图形,若∠A=30°,∠C=90°,OC=1,则AB的长为 .
20、如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24cm,△OAB的周长是18cm,则EF=____cm.
21、如图所示,在四边形ABCD中,AB=CD,BC=AD,E,F为对角线AC上的点,且AE=CF,若BE=4,则DF= .
22、如图所示,B、C、E三点在一条直线上,△ABC 和△DCE均为等边三角形,连结AE、DB.若AB=5,AE=12,则DB= .
三、解答题:
23、两个正多边形的边数之比为1∶2,内角和之比为3∶8,求这两个多边形的边数、内角和.
24、如图所示,在四边形ABCD中,DC∥AB,以AD,AC为边作□ACED,延长DC交EB于F,求证:EF=FB.
25、如图,点D,E分别在边AB,AC上,BD=CE,BE,CD的中点分别是M,N,直线MN分别交AB,AC于点P,Q.求证:AP=AQ.
26、如图所示,梯形ABCD中,AD∥BC,F、H分别是AB、CD的中点, FH分别交BD、AC于G、M, BD=6,ED=2,BC=10.
(1)求GM的长;(2)若梯形ABCD是等腰梯形,求证:△BFG≌△CHM.
27、如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)若AB=6,求平行四边形BCFD的面积.
参考答案
一、选择题:
1、D 2、C 3、D 4、B 5、A 6、D
7、C 8、D 9、C 10、A 11、A 12、C
二、填空题:
13、到线段两端距离相等的点在这条线段的垂直平分线上,真.
14、4
15、两;有且只有一条直线;原命题成立
16、平行四边形
17、70°
18、90°
19、4
20、3
21、4
22、12
三、解答题:
23、五边形,540°;十边形,1440°
24、过点B作BG∥AD,交DC的延长线于G,连接EG.
∵DC∥AB,∴ABGD是平行四边形,∴BG AD.
在□ACED中,ADCE,∴CEBG.
∴四边形BCEG为平行四边形,∴EF=FB.
25、取BC的中点K,连结KM,KN,
∴KM,KN分别是△BCE和△BCD的中位线,
∴KM∥AC,KM=CE,KN∥AB,KN=BD,
∴∠AQP=∠KMN,∠APQ=∠KNM,
又∵BD=CE,∴KM=KN,∴∠KMN=∠KNM,
∴∠APQ=∠AQP,∴AP=AQ
26、∵F、H为AB、CD的中点,∴AD∥FH∥BC.
∴△AED∽△CEB.∴,∴.∴AD=5.
又∵△AED∽△MEC,∴.∴,∴MG=.
(2)∵等腰梯形ABCD中F、H分别是AB、CD的中点,
∴BF=CH,∠BAD=∠CDA,FH∥AD.∴∠BFG=∠CHM.
∴FG=HM=AD.∴△BFG≌△CHM.
27、(1)证明:在△ABC中,∠ACB=90°,∠CAB=30°,∴∠ABC=60°.
在等边△ABD中,∠BAD=60°,∴∠BAD=∠ABC=60°.
∵E为AB的中点,∴AE=BE.
又∵∠AEF=∠BEC,∴△AEF≌△BEC.
在△ABC中,∠ACB=90°,E为AB的中点,∴CE=AB,BE=AB.
∴CE=AE,∴∠EAC=∠ECA=30°,∴∠BCE=∠EBC=60°.
又∵△AEF≌△BEC,∴∠AFE=∠BCE=60°.
又∵∠D=60°,∴∠AFE=∠D=60°.∴FC∥BD.
又∵∠BAD=∠ABC=60°,∴AD∥BC,即FD∥BC.
∴四边形BCFD是平行四边形.
(2)解:在Rt△ABC中,∵∠BAC=30°,AB=6,
∴BC=AB=3,AC=BC=3,∴S=3×=9.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
