(公开课)5.2 等式的基本性质 课件(21张PPT)
文档属性
| 名称 | (公开课)5.2 等式的基本性质 课件(21张PPT) |  | |
| 格式 | rar | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-22 16:20:54 | ||
图片预览




文档简介
5.2 等式的基本性质
梅溪中学 刘向萍
(1) (2)
(3) (4)
(5) (6)
下列各式中,哪些是一元一次方程?
?
?
?
?
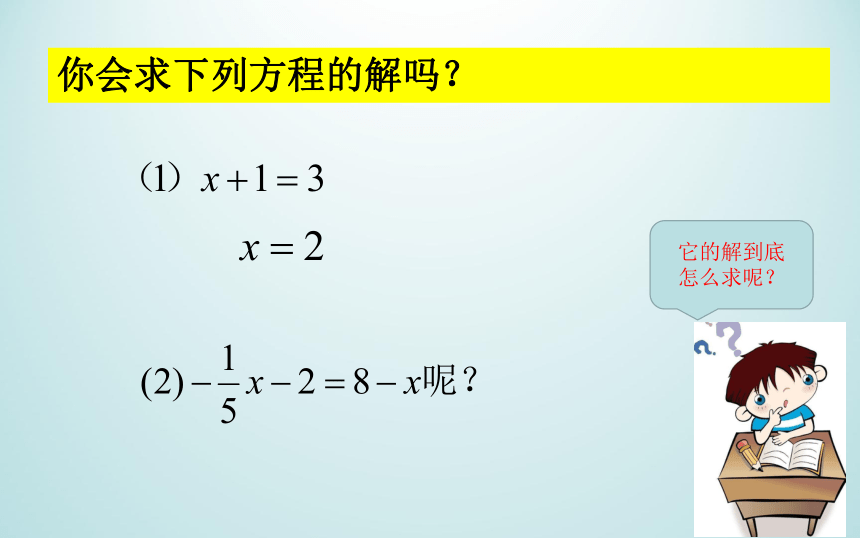
你会求下列方程的解吗?
它的解到底
怎么求呢?
a
b
b
b
a
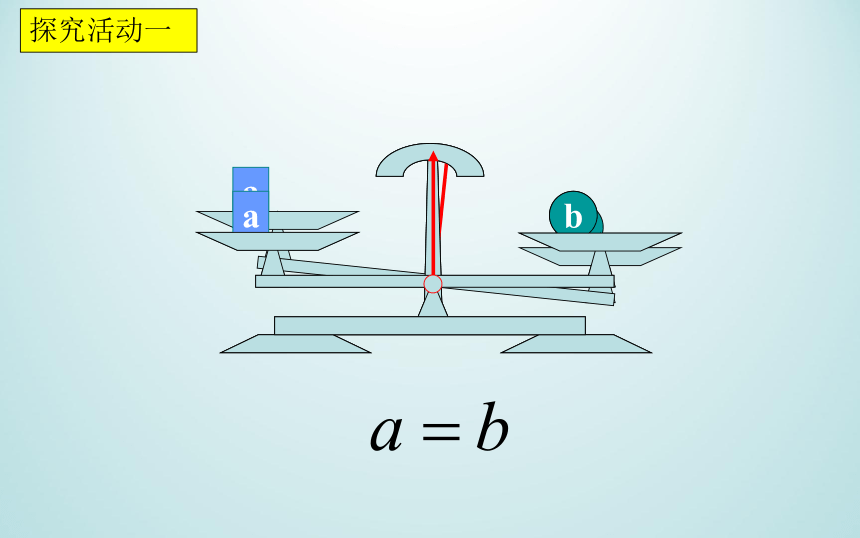
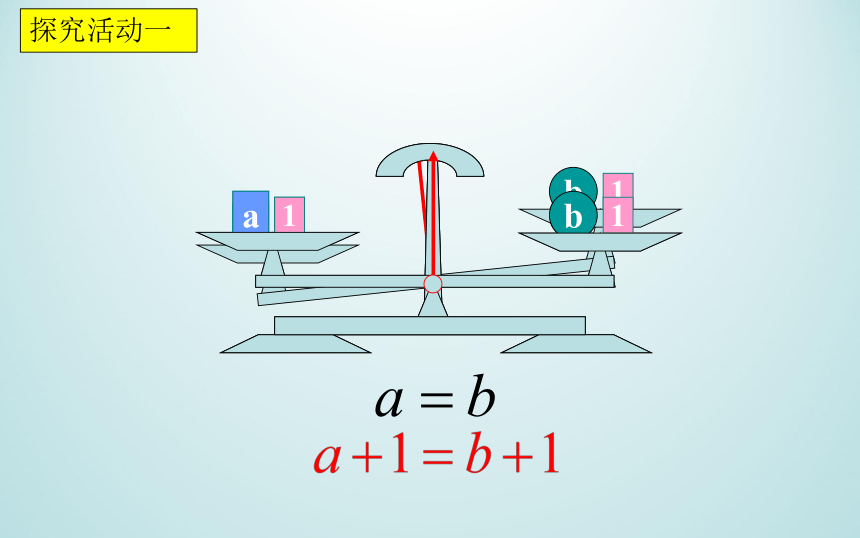
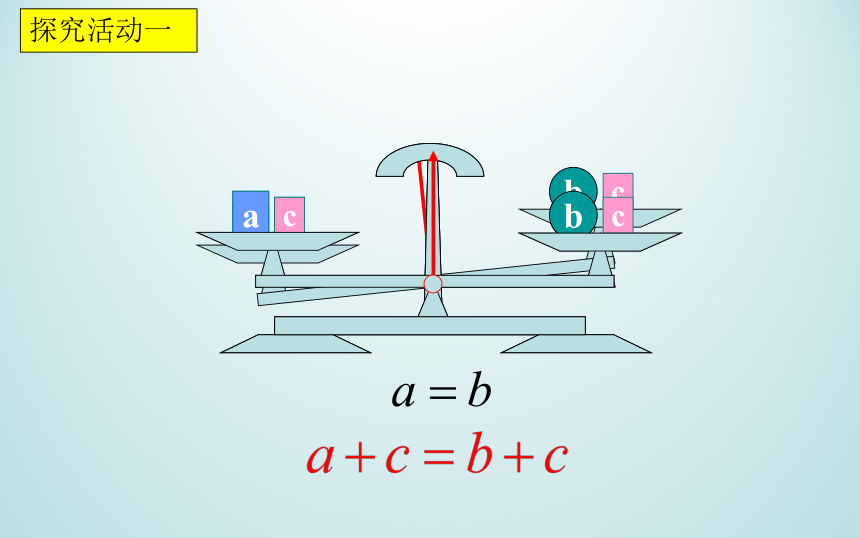
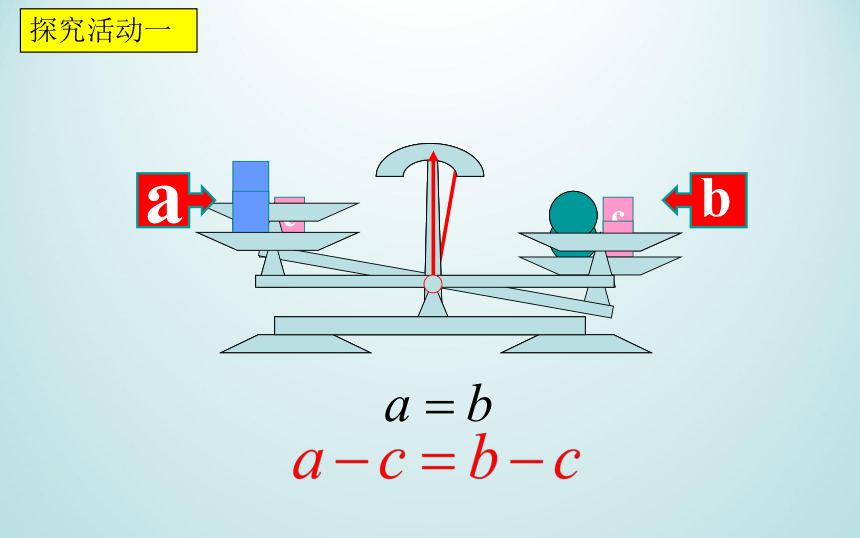
探究活动一
1
b
a
1
a
b
1
1
a
b
1
探究活动一
c
b
a
c
a
b
c
c
a
b
c
探究活动一
c
c
c
a
b
探究活动一
引发思考
结合刚才发现的两个规律,你能试着用一句话表述清楚吗?
等式两边同时加上(或都减去)同一个数或式,所得结果仍是等式.
等式的性质1:
用字母可表示为:
如果 ,那么 .
a
b
a
a
a
b
b
a
a
b
b
…
…
b
a
b
a
b
a
b
a
b
a
C个
C个
探究活动二
c ≠ 0
等式的性质2:
等式两边都乘或都除以同一个的数或式(除数不为零),所得结果仍是等式.
用字母可表示为:
如果 ,那么 .
试一试:
1. 判断下面变形是否正确?并说明理由.
?
?
?
?
(1)
(2)
(3)
(4)
看成一个整体
2. 根据下列各题的条件,写出仍然成立的等式.
试一试:
已知 ,判断下列等式是否成立,并说明理由.
例1:
且
试一试:
3. 用适当的数或式子填空,使所得结果仍是等式.
(1)如果 ,
那么 ( )
即 x =
(2)如果 ,
那么 = 6 ( )
等式性质1
等式性质2
结论:
求方程的解,就是将方程变形为 的形式,变形的依据就是等式的基本性质.
例2,利用等式的性质解下列方程,并写出检验过程:
(1)
(2)
利用等式的性质解下列方程,并写出检验过程:
(1)
(2)
练一练
超越自我
课堂总结
1.等式的性质有几条?
2.用字母怎么表示?
3.解方程最终必须将方程 化成什么形式?变形的依据是什么?
作业布置:
1.作业本5.2
2.(选做)全品
梅溪中学 刘向萍
(1) (2)
(3) (4)
(5) (6)
下列各式中,哪些是一元一次方程?
?
?
?
?
你会求下列方程的解吗?
它的解到底
怎么求呢?
a
b
b
b
a
探究活动一
1
b
a
1
a
b
1
1
a
b
1
探究活动一
c
b
a
c
a
b
c
c
a
b
c
探究活动一
c
c
c
a
b
探究活动一
引发思考
结合刚才发现的两个规律,你能试着用一句话表述清楚吗?
等式两边同时加上(或都减去)同一个数或式,所得结果仍是等式.
等式的性质1:
用字母可表示为:
如果 ,那么 .
a
b
a
a
a
b
b
a
a
b
b
…
…
b
a
b
a
b
a
b
a
b
a
C个
C个
探究活动二
c ≠ 0
等式的性质2:
等式两边都乘或都除以同一个的数或式(除数不为零),所得结果仍是等式.
用字母可表示为:
如果 ,那么 .
试一试:
1. 判断下面变形是否正确?并说明理由.
?
?
?
?
(1)
(2)
(3)
(4)
看成一个整体
2. 根据下列各题的条件,写出仍然成立的等式.
试一试:
已知 ,判断下列等式是否成立,并说明理由.
例1:
且
试一试:
3. 用适当的数或式子填空,使所得结果仍是等式.
(1)如果 ,
那么 ( )
即 x =
(2)如果 ,
那么 = 6 ( )
等式性质1
等式性质2
结论:
求方程的解,就是将方程变形为 的形式,变形的依据就是等式的基本性质.
例2,利用等式的性质解下列方程,并写出检验过程:
(1)
(2)
利用等式的性质解下列方程,并写出检验过程:
(1)
(2)
练一练
超越自我
课堂总结
1.等式的性质有几条?
2.用字母怎么表示?
3.解方程最终必须将方程 化成什么形式?变形的依据是什么?
作业布置:
1.作业本5.2
2.(选做)全品
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
