26.2.2 二次函数y=ax2+bx+c的图象与性质 课件(30张PPT)
文档属性
| 名称 | 26.2.2 二次函数y=ax2+bx+c的图象与性质 课件(30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 388.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-05 08:24:05 | ||
图片预览







文档简介
课件30张PPT。2.二次函数y=ax2+bx+c的图象与性质26.2 二次函数的图象与性质第26章 二次函数情境引入1.会用配方法或公式法将一般式y=ax2+bx+c化成顶点式y=a(x-h)2+k.(难点)
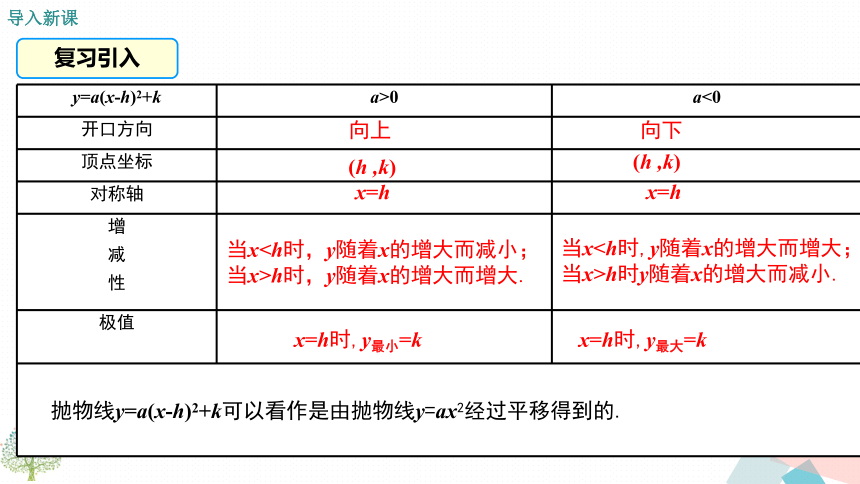
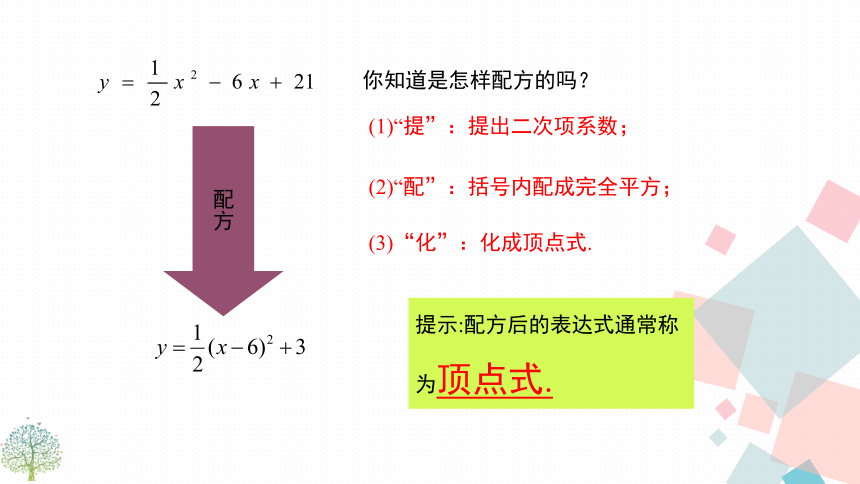
2.会熟练求出二次函数一般式y=ax2+bx+c的顶点坐标、对称轴.(重点)导入新课复习引入向上向下(h ,k)(h ,k)x=hx=h当xh时,y随着x的增大而增大. 当xh时y随着x的增大而减小. x=h时,y最小=kx=h时,y最大=k抛物线y=a(x-h)2+k可以看作是由抛物线y=ax2经过平移得到的.(0,0)y轴最大值0(0,-5)y轴最大值-5(-2,0)直线x=-2最大值0 (-2,-4)直线x=-2最大值-4(4,3)直线x=4最小值3??????讲授新课探究归纳配方可得配方你知道是怎样配方的吗? (1)“提”:提出二次项系数;(2)“配”:括号内配成完全平方;(3)“化”:化成顶点式.提示:配方后的表达式通常称为顶点式.答:对称轴是直线x=6,顶点坐标是(6,3).答:平移方法1:
先向上平移3个单位,再向右平移6个单位得到的;
平移方法2:
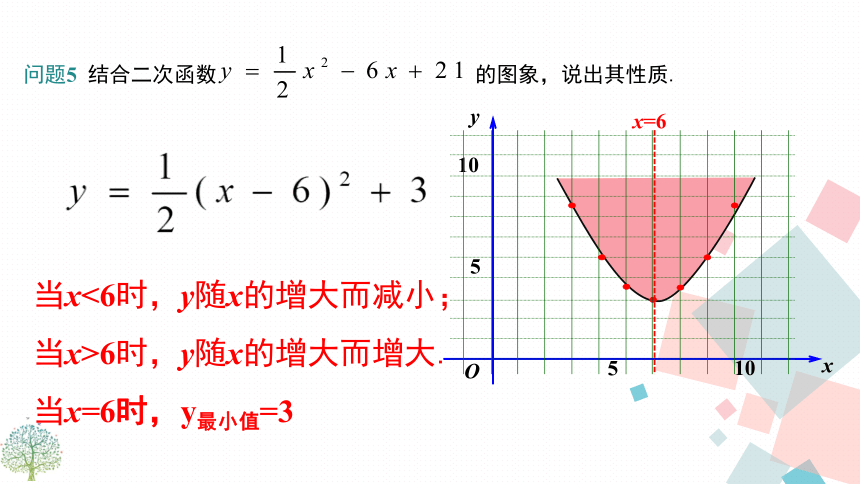
先向右平移6个单位,再向上平移3个单位得到的.问题4 如何用描点法画二次函数 的图象?解: 先利用图形的对称性列表7.553.533.557.5然后描点画图,得到图象如右图.O问题5 结合二次函数 的图象,说出其性质.x=6当x<6时,y随x的增大而减小;
当x>6时,y随x的增大而增大.
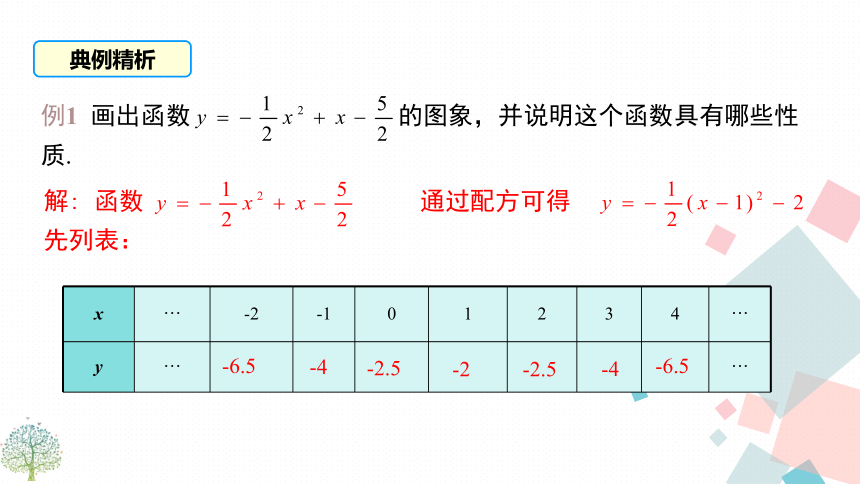
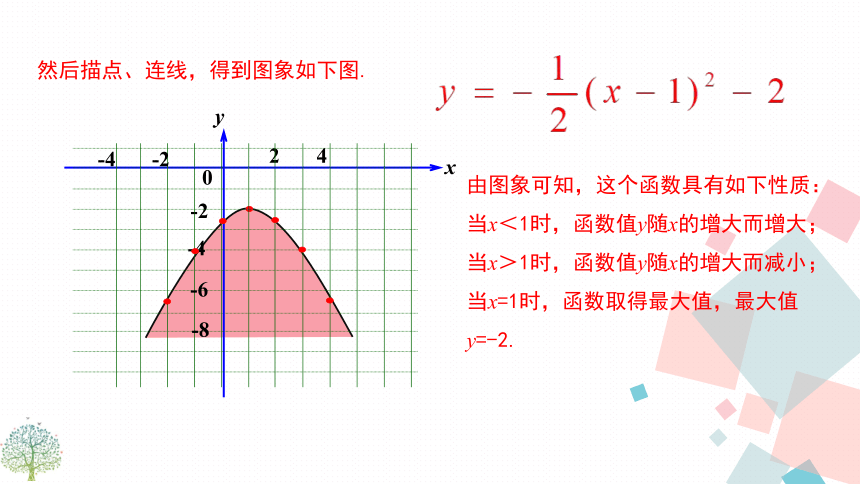
当x=6时,y最小值=3 O-6.5-4-2.5-2-2.5-4-6.5典例精析然后描点、连线,得到图象如下图.由图象可知,这个函数具有如下性质:
当x<1时,函数值y随x的增大而增大;
当x>1时,函数值y随x的增大而减小;
当x=1时,函数取得最大值,最大值y=-2. 求二次函数y=2x2-8x+7图象的对称轴和顶点坐标. 因此,二次函数y=2x2-8x+7图象的对称轴是直线x=2,顶点坐标为(2,-1).解:练一练 我们如何用配方法将一般式y=ax2+bx+c(a≠0)化成顶点式y=a(x-h)2+k?配方法有些麻烦,那么有没有更简单的方法呢?y=ax2+bx+c 归纳总结二次函数y=ax2+bx+c的图象和性质归纳总结二次函数y=ax2+bx+c的图象和性质(1)(2)如果a>0,当x< 时,y随x的增大而减小;当x> 时,y随x的增大而增大.如果a<0,当x< 时,y随x的增大而增大;当x> 时,y随x的增大而减小.例2 已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )
A.b≥-1 B.b≤-1
C.b≥1 D.b≤1D填一填(1,3)x=1最大值1(0,-1)y轴最大值-1最小值-6合作探究问题1 一次函数y=kx+b的图象如下图所示,请根据一次函数图象的性质填空:>><>>问题2 二次函数 的图象如下图所示,请根据二次函数的性质填空:>>>><=x=0时,y=c.<=><><x=0时,y=c.二次函数y=ax2+bx+c的图象与a、b、c的关系向上向下y左右 正负知识要点例3 已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2. 其中正确的个数是 ( )
A.1 B.2 C.3 D.4D由图象上横坐标为 x=-2的点在第三象限可得4a-2b+c<0,故③正确; 由图象上x=1的点在第四象限得a+b+c<0,由图象上x=-1的点在第二象限得出 a-b+c>0,则(a+b+c)(a-b+c)<0,即(a+c)2-b2<0,可得(a+c)2<b2,故④正确.【解析】由图象开口向下可得a<0,由对称轴在y轴左侧可得b<0,由图象与y轴交于正半轴可得 c>0,则abc>0,故①正确;由对称轴x>-1可得2a-b<0,故②正确;练一练解析:由二次函数的图象得知:a<0,b>0.故反比例函数的图象在二、四象限,正比例函数的图象经过一、三象限.即正确答案是C.C1.已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:A.y轴 B.直线x=
C. 直线x=2 D.直线x= 则该二次函数图象的对称轴为( )D当堂练习2.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
(1)a、b同号;
(2)当x=–1和x=3时,函数值相等;
(3) 4a+b=0;
(4)当y=–2时,x的值只能取0;
其中正确的是 .直线x=1(2)3.如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c= -9a;④若(-3,y1),( ,y2)是抛物线上两点,则y1>y2.其中正确的是( )A.①②③ B.①③④ C.①②④ D.②③④yO2x=-1Bx4.根据公式确定下列二次函数图象的对称轴和顶点坐标:直线x=3直线x=8直线x=1.25直线x= 0.5课堂小结顶点:对称轴:y=ax2+bx+c(a ≠0)
(一般式)配方法公式法
2.会熟练求出二次函数一般式y=ax2+bx+c的顶点坐标、对称轴.(重点)导入新课复习引入向上向下(h ,k)(h ,k)x=hx=h当x
先向上平移3个单位,再向右平移6个单位得到的;
平移方法2:
先向右平移6个单位,再向上平移3个单位得到的.问题4 如何用描点法画二次函数 的图象?解: 先利用图形的对称性列表7.553.533.557.5然后描点画图,得到图象如右图.O问题5 结合二次函数 的图象,说出其性质.x=6当x<6时,y随x的增大而减小;
当x>6时,y随x的增大而增大.
当x=6时,y最小值=3 O-6.5-4-2.5-2-2.5-4-6.5典例精析然后描点、连线,得到图象如下图.由图象可知,这个函数具有如下性质:
当x<1时,函数值y随x的增大而增大;
当x>1时,函数值y随x的增大而减小;
当x=1时,函数取得最大值,最大值y=-2. 求二次函数y=2x2-8x+7图象的对称轴和顶点坐标. 因此,二次函数y=2x2-8x+7图象的对称轴是直线x=2,顶点坐标为(2,-1).解:练一练 我们如何用配方法将一般式y=ax2+bx+c(a≠0)化成顶点式y=a(x-h)2+k?配方法有些麻烦,那么有没有更简单的方法呢?y=ax2+bx+c 归纳总结二次函数y=ax2+bx+c的图象和性质归纳总结二次函数y=ax2+bx+c的图象和性质(1)(2)如果a>0,当x< 时,y随x的增大而减小;当x> 时,y随x的增大而增大.如果a<0,当x< 时,y随x的增大而增大;当x> 时,y随x的增大而减小.例2 已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )
A.b≥-1 B.b≤-1
C.b≥1 D.b≤1D填一填(1,3)x=1最大值1(0,-1)y轴最大值-1最小值-6合作探究问题1 一次函数y=kx+b的图象如下图所示,请根据一次函数图象的性质填空:>><>>问题2 二次函数 的图象如下图所示,请根据二次函数的性质填空:>>>><=x=0时,y=c.<=><><x=0时,y=c.二次函数y=ax2+bx+c的图象与a、b、c的关系向上向下y左右 正负知识要点例3 已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2. 其中正确的个数是 ( )
A.1 B.2 C.3 D.4D由图象上横坐标为 x=-2的点在第三象限可得4a-2b+c<0,故③正确; 由图象上x=1的点在第四象限得a+b+c<0,由图象上x=-1的点在第二象限得出 a-b+c>0,则(a+b+c)(a-b+c)<0,即(a+c)2-b2<0,可得(a+c)2<b2,故④正确.【解析】由图象开口向下可得a<0,由对称轴在y轴左侧可得b<0,由图象与y轴交于正半轴可得 c>0,则abc>0,故①正确;由对称轴x>-1可得2a-b<0,故②正确;练一练解析:由二次函数的图象得知:a<0,b>0.故反比例函数的图象在二、四象限,正比例函数的图象经过一、三象限.即正确答案是C.C1.已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:A.y轴 B.直线x=
C. 直线x=2 D.直线x= 则该二次函数图象的对称轴为( )D当堂练习2.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
(1)a、b同号;
(2)当x=–1和x=3时,函数值相等;
(3) 4a+b=0;
(4)当y=–2时,x的值只能取0;
其中正确的是 .直线x=1(2)3.如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c= -9a;④若(-3,y1),( ,y2)是抛物线上两点,则y1>y2.其中正确的是( )A.①②③ B.①③④ C.①②④ D.②③④yO2x=-1Bx4.根据公式确定下列二次函数图象的对称轴和顶点坐标:直线x=3直线x=8直线x=1.25直线x= 0.5课堂小结顶点:对称轴:y=ax2+bx+c(a ≠0)
(一般式)配方法公式法
