26.2.2二次函数y=ax2+bx+c的图象与性质 课件 (14张PPT)
文档属性
| 名称 | 26.2.2二次函数y=ax2+bx+c的图象与性质 课件 (14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 303.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-04 17:02:51 | ||
图片预览





文档简介
课件14张PPT。2.二次函数y=ax2+bx+c的图象与性质
第4课时 函数y=ax2+bx+c的图象与性质华东师大版 九年级下册情景导入 由前面的知识,我们知道,函数 的图象,向上平移2个单位,可以得到函数 的图象;函数 的图象,向右平移3个单位,可以得到函数 的图象,那么函数 的图象,如何平移,才能得到函数 的图象呢?
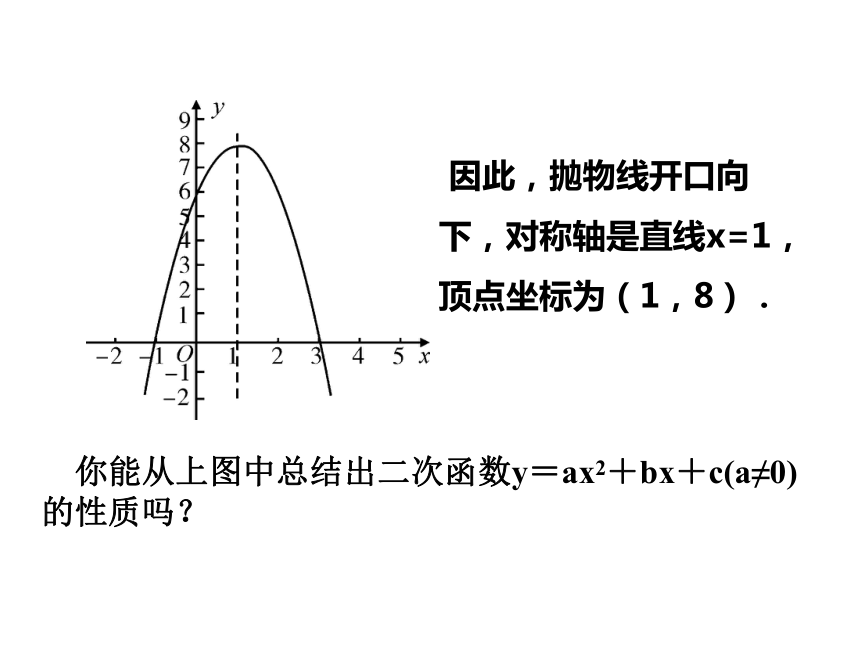
函数y=-4(x-2)2+1具有哪些性质?获取新知 因此,抛物线开口向下,对称轴是直线x=1,顶点坐标为(1,8). 你能从上图中总结出二次函数y=ax2+bx+c(a≠0)的性质吗?【归纳结论】
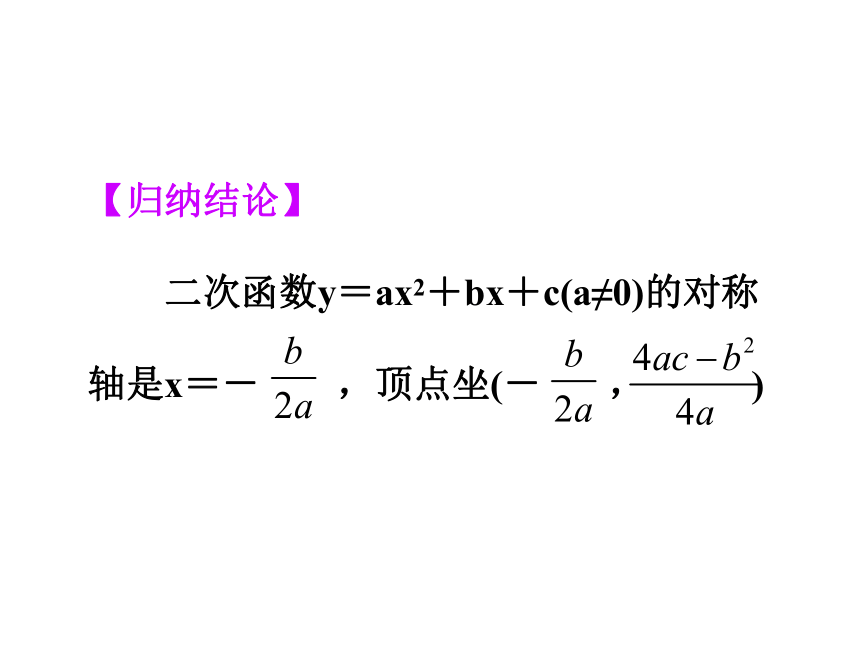
二次函数y=ax2+bx+c(a≠0)的对称
轴是x=- ,顶点坐(- , )运用新知1、函数y=x2-2x+3的图象的顶点坐标是( ) A. (1,-4) B.(-1,2)
C. (1,2) D.(0,3)解析:法一,直接用二次函数顶点坐标公式求.
法二,将二次函数解析式由一般形式转换为顶点式,即y=a(x-h)2+k的形式,顶点坐标即为(h,k),y=x2-2x+3=(x-1)2+2,所以顶点坐标为(1,2),答案选C.C2、抛物线 的对称轴是( )
A. x=-2 B.x=2
C. x=-4 D. x=4B 解析:由图象,抛物线开口方向向下,
∴ a<0
抛物线对称轴在y轴右侧,
∴ 又∵a<0,b>0,∴ab<0,
抛物线与y轴交点坐标为(0,c)点,由图知,该点在x轴上方, ∴c>0.
答案选C.3、已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中,正确的是( ) A. ab>0,c>0 B. ab>0,c<0 C. ab<0,c>0 D. ab<0,c<0C4、把抛物线 的图象向左平移2个单位,再向上平移3个单位,所得的抛物线的函数关系式是( ) A. B.
C. D.C5、已知抛物线 的顶点在坐标轴上,求a的值.分析:顶点在坐标轴上有两种可能:
(1)顶点在x轴上,则顶点的纵坐标等于0;
(2)顶点在y轴上,则顶点的横坐标等于0.课堂小结 课后作业1.从教材练习中选取;
2.完成练习册中本课时的习题。 不存在没有热情的智能,也不存在没有知能的热情,如果没有勤奋,也不存在热情与才能的结合。——约瑟夫
第4课时 函数y=ax2+bx+c的图象与性质华东师大版 九年级下册情景导入 由前面的知识,我们知道,函数 的图象,向上平移2个单位,可以得到函数 的图象;函数 的图象,向右平移3个单位,可以得到函数 的图象,那么函数 的图象,如何平移,才能得到函数 的图象呢?
函数y=-4(x-2)2+1具有哪些性质?获取新知 因此,抛物线开口向下,对称轴是直线x=1,顶点坐标为(1,8). 你能从上图中总结出二次函数y=ax2+bx+c(a≠0)的性质吗?【归纳结论】
二次函数y=ax2+bx+c(a≠0)的对称
轴是x=- ,顶点坐(- , )运用新知1、函数y=x2-2x+3的图象的顶点坐标是( ) A. (1,-4) B.(-1,2)
C. (1,2) D.(0,3)解析:法一,直接用二次函数顶点坐标公式求.
法二,将二次函数解析式由一般形式转换为顶点式,即y=a(x-h)2+k的形式,顶点坐标即为(h,k),y=x2-2x+3=(x-1)2+2,所以顶点坐标为(1,2),答案选C.C2、抛物线 的对称轴是( )
A. x=-2 B.x=2
C. x=-4 D. x=4B 解析:由图象,抛物线开口方向向下,
∴ a<0
抛物线对称轴在y轴右侧,
∴ 又∵a<0,b>0,∴ab<0,
抛物线与y轴交点坐标为(0,c)点,由图知,该点在x轴上方, ∴c>0.
答案选C.3、已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中,正确的是( ) A. ab>0,c>0 B. ab>0,c<0 C. ab<0,c>0 D. ab<0,c<0C4、把抛物线 的图象向左平移2个单位,再向上平移3个单位,所得的抛物线的函数关系式是( ) A. B.
C. D.C5、已知抛物线 的顶点在坐标轴上,求a的值.分析:顶点在坐标轴上有两种可能:
(1)顶点在x轴上,则顶点的纵坐标等于0;
(2)顶点在y轴上,则顶点的横坐标等于0.课堂小结 课后作业1.从教材练习中选取;
2.完成练习册中本课时的习题。 不存在没有热情的智能,也不存在没有知能的热情,如果没有勤奋,也不存在热情与才能的结合。——约瑟夫
