浙教版数学八年级下册 第一章二次根式复习课件(共18张PPT)
文档属性
| 名称 | 浙教版数学八年级下册 第一章二次根式复习课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 127.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-08 22:48:17 | ||
图片预览






文档简介
课件18张PPT。 二次根式复习课课前2分钟朗读内容:课程标准要求:
1.了解二次根式的概念,了解简单二次根式的字母取值范围.2.了解二次根式的性质及其加、减、乘、除运算法则.
3.会用二次根式的性质和运算法则进行有关实数的简单四则运算.
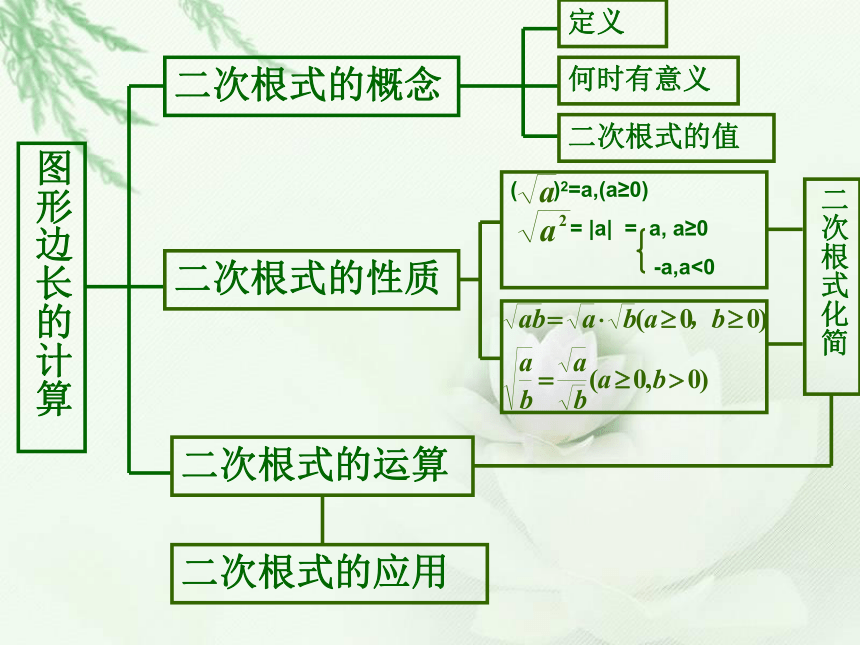
(不要求分母有理化)图形边长的计算二次根式的概念定义何时有意义二次根式的值二次根式的性质( )2=a,(a≥0)
= |a| = a, a≥0
-a,a<0二次根式化简二次根式的运算二次根式的应用本章主要性质与法则:a,a<0练习:1.计算 的结果是… … … … … …( )
(A) -3 (B) ±9 (C) 3 (D) 92.化简 的结果是… … … … … …( )
(A) (B) (C) (D)
3. 的结果是… … … … … …( )
(A) 3 (B) (C) (D)
4.已知x<2,则化简 的结果 …( )
(A) x-2 (B) x+2 (C) –x-2 (D) 2-x
CBBD5.要使式子 有意义,字母x的取值必须满足…… ……………………………… …… ( )
(A) x>-1.5 (B) x≥-1.5 (C) x>1.5(D) x≥1.5
6. 当x为实数时,下列式子中一定有意义的是( )
(A) (B) (C) (D)
7.式子 中的x的取值范围是____________.8. 成立的条件是__________.9.已知a= ,b= ,则a2-ab+b2=______.10.计算 =_______.BCx≥0且x≠12则它的面积为_____,
AC边上的高是______.hh=11.如图,小正方形的边长为1,连结小正方形的三个顶点可得△ABC,AC边上的高是______.ABC12.设实数 的整数部分为a,小数部分为b,则 (2a+b)(2a-b)=________.a=2,b=(2a+b)(2a-b)=13.在△ABC中,已知AB=1,AC= ,
∠C=30°,∠ABC=45°,求△ABC的面积。ABC13.在△ABC中,已知AB=1,AC= ,
∠C=30°,∠ABC=45°,求△ABC的面积。ABC解:如图所示,过点A作AD⊥BC,垂足为D.
D∵ AB=1,∠ABC=45° AD⊥BC∴AD=BD=又∵AC= ,∠C=30°,14.如图,一次函数
的图象与x轴、y轴交于A、B两点,
求坐标原点O到直线AB的距离。OBADxy 14.如图,一次函数 的图象与x轴、y轴交于A、B两点,求坐标原点O到直线AB的距离。OBADxy解:根据题意,可知A、B两点的坐标分别为A( ,0),B(0, ).即OA= ,OB= ,∴坐标原点O到直线AB的距离OABCyx15.在平面直角坐标系中,
四边形OABC是等腰梯形,BC//OA,OA=10,AB=4,∠COA=45°,
点P为x轴正半轴上由O向A运动的一个动点,点P不与点O、A重合。
(1)求点B的坐标和直线AB的解析式;
(2)点P运动到什么位置时,△OCP为
等腰三角形?求这时点P的坐标.OABCyx15.在平面直角坐标系中,
四边形OABC是等腰梯形,BC//OA,OA=10,AB=4,∠COA=45°,
点P为x轴正半轴上由O向A运动的一个动点,点P不与点O、A重合。
(1)求点B的坐标和直线AB的解析式;解:过点B作BF⊥OA于F.F∵AB=4, ∠COA=∠BAO=45 °,∴点B的坐标是( )∵点A的坐标(10,0), 设直线AB的解析式为y=kx+b(k≠0)
10k+b=0∴ k=-1,b=10 ∴直线AB的解析式为 y=-x+10OABCyx(2)点P运动到什么位置时,△OCP为等腰三角形?求这时点P的坐标.(3) 当OP=CP时,P( ,0)P1 当CO=CP时,P( ,0) 当OP=OC时,P (4,0)P2P316.如图,正方形ABFG与正方形BCDE的面积和为7,AD2-CG2=3,求AC与EF的乘积.ABCDEFG<分析>本例先设两个正方形的面积为a,b,则它们的边长分别可用 表示.这样利用图形的性质就得到以a,b为未知数的简单方程,从而使问题得到解决.16.如图,正方形ABFG与正方形BCDE的面积和为7,AD2-CG2=3,求AC与EF的乘积.ABCDEFG解:设正方形BCDE和正方形ABFG的面积为a,b,则它们的边长分别可用 表示.在Rt△ACD和 Rt△CAG中,∴AD2-CG2=a-b由已知得 a+b=7
a-b=3解得 a=5
b=2
∴ AC与EF的乘积=小结 本节课有何学习收获
和学习感悟?
3.会用二次根式的性质和运算法则进行有关实数的简单四则运算.
(不要求分母有理化)图形边长的计算二次根式的概念定义何时有意义二次根式的值二次根式的性质( )2=a,(a≥0)
= |a| = a, a≥0
-a,a<0二次根式化简二次根式的运算二次根式的应用本章主要性质与法则:a,a<0练习:1.计算 的结果是… … … … … …( )
(A) -3 (B) ±9 (C) 3 (D) 92.化简 的结果是… … … … … …( )
(A) (B) (C) (D)
3. 的结果是… … … … … …( )
(A) 3 (B) (C) (D)
4.已知x<2,则化简 的结果 …( )
(A) x-2 (B) x+2 (C) –x-2 (D) 2-x
CBBD5.要使式子 有意义,字母x的取值必须满足…… ……………………………… …… ( )
(A) x>-1.5 (B) x≥-1.5 (C) x>1.5(D) x≥1.5
6. 当x为实数时,下列式子中一定有意义的是( )
(A) (B) (C) (D)
7.式子 中的x的取值范围是____________.8. 成立的条件是__________.9.已知a= ,b= ,则a2-ab+b2=______.10.计算 =_______.BCx≥0且x≠12
AC边上的高是______.hh=11.如图,小正方形的边长为1,连结小正方形的三个顶点可得△ABC,AC边上的高是______.ABC12.设实数 的整数部分为a,小数部分为b,则 (2a+b)(2a-b)=________.a=2,b=(2a+b)(2a-b)=13.在△ABC中,已知AB=1,AC= ,
∠C=30°,∠ABC=45°,求△ABC的面积。ABC13.在△ABC中,已知AB=1,AC= ,
∠C=30°,∠ABC=45°,求△ABC的面积。ABC解:如图所示,过点A作AD⊥BC,垂足为D.
D∵ AB=1,∠ABC=45° AD⊥BC∴AD=BD=又∵AC= ,∠C=30°,14.如图,一次函数
的图象与x轴、y轴交于A、B两点,
求坐标原点O到直线AB的距离。OBADxy 14.如图,一次函数 的图象与x轴、y轴交于A、B两点,求坐标原点O到直线AB的距离。OBADxy解:根据题意,可知A、B两点的坐标分别为A( ,0),B(0, ).即OA= ,OB= ,∴坐标原点O到直线AB的距离OABCyx15.在平面直角坐标系中,
四边形OABC是等腰梯形,BC//OA,OA=10,AB=4,∠COA=45°,
点P为x轴正半轴上由O向A运动的一个动点,点P不与点O、A重合。
(1)求点B的坐标和直线AB的解析式;
(2)点P运动到什么位置时,△OCP为
等腰三角形?求这时点P的坐标.OABCyx15.在平面直角坐标系中,
四边形OABC是等腰梯形,BC//OA,OA=10,AB=4,∠COA=45°,
点P为x轴正半轴上由O向A运动的一个动点,点P不与点O、A重合。
(1)求点B的坐标和直线AB的解析式;解:过点B作BF⊥OA于F.F∵AB=4, ∠COA=∠BAO=45 °,∴点B的坐标是( )∵点A的坐标(10,0), 设直线AB的解析式为y=kx+b(k≠0)
10k+b=0∴ k=-1,b=10 ∴直线AB的解析式为 y=-x+10OABCyx(2)点P运动到什么位置时,△OCP为等腰三角形?求这时点P的坐标.(3) 当OP=CP时,P( ,0)P1 当CO=CP时,P( ,0) 当OP=OC时,P (4,0)P2P316.如图,正方形ABFG与正方形BCDE的面积和为7,AD2-CG2=3,求AC与EF的乘积.ABCDEFG<分析>本例先设两个正方形的面积为a,b,则它们的边长分别可用 表示.这样利用图形的性质就得到以a,b为未知数的简单方程,从而使问题得到解决.16.如图,正方形ABFG与正方形BCDE的面积和为7,AD2-CG2=3,求AC与EF的乘积.ABCDEFG解:设正方形BCDE和正方形ABFG的面积为a,b,则它们的边长分别可用 表示.在Rt△ACD和 Rt△CAG中,∴AD2-CG2=a-b由已知得 a+b=7
a-b=3解得 a=5
b=2
∴ AC与EF的乘积=小结 本节课有何学习收获
和学习感悟?
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
