26.2.2 第1课时 二次函数y=ax2+k的图象与性质 课件
文档属性
| 名称 | 26.2.2 第1课时 二次函数y=ax2+k的图象与性质 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-20 17:09:20 | ||
图片预览



文档简介
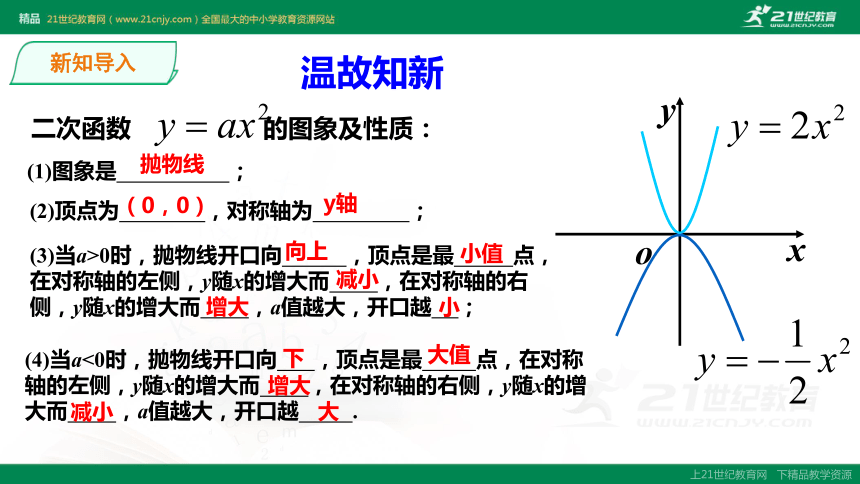
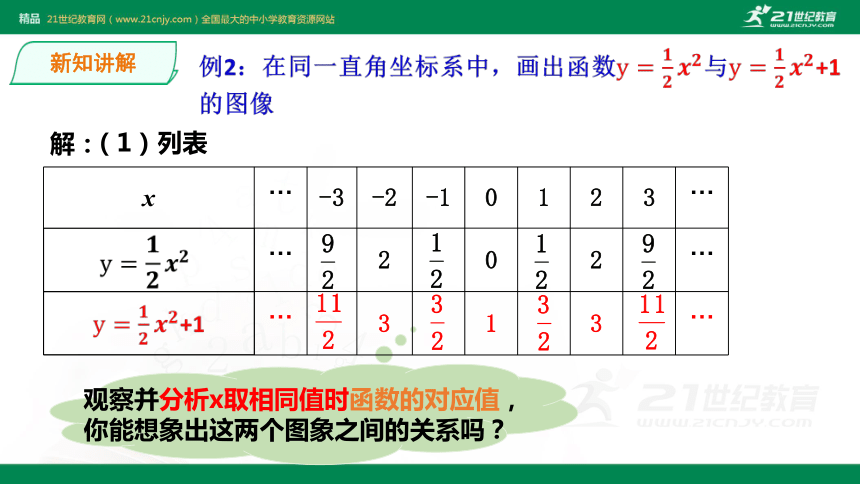
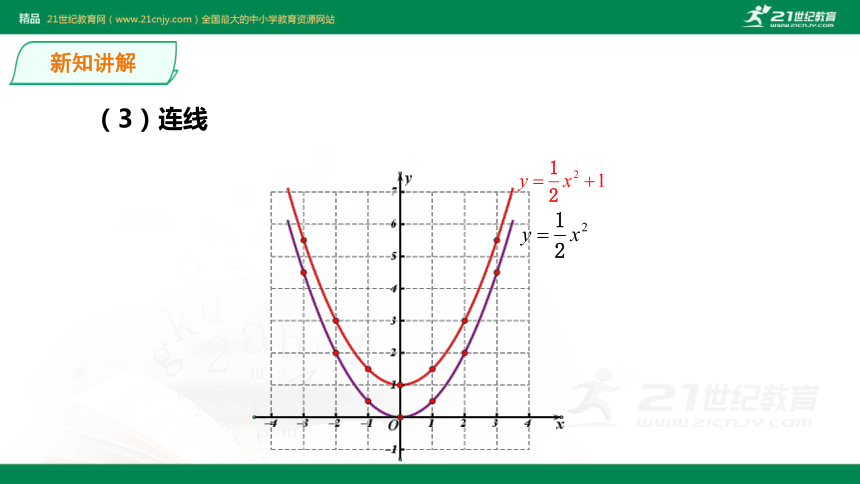
课件19张PPT。华师大版 九年级下26.2 二次函数的图象与性质第1节 二次函数y=ax2的图象与性质第1课时 二次函数y=ax2+k的图象与性质温故知新二次函数 的图象及性质:(1)图象是 ;(2)顶点为 ,对称轴为 ;(4)当a<0时,抛物线开口向 ,顶点是最 点,在对称轴的左侧,y随x的增大而 ,在对称轴的右侧,y随x的增大而 ,a值越大,开口越 .(3)当a>0时,抛物线开口向 ,顶点是最 点,在对称轴的左侧,y随x的增大而 ,在对称轴的右侧,y随x的增大而 ,a值越大,开口越 ;抛物线(0,0)y轴向上小值减小增大小下大值增大减小大探究1:分析:将函数关系式配方,得??解:(1)列表观察并分析x取相同值时函数的对应值,你能想象出这两个图象之间的关系吗?(2)描点(2)描点(3)连线对称轴相同比较两个函数图象的共性和区别:小组讨论(0,0)(0,1)y轴y轴在x轴的上方(除顶点外)在x轴的上方向上向上当x=0时,最小值为0当x=0时,最小值为1对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 抛物线顶点坐标对称轴位置开口方向增减性最值?顶点不同
最值不同增减性相同探索:观察下表思考这两个函数的图象的形状相同吗?提示:用平移的方法????2+10+1????2+1思考:自变量x取同一值时,两个函数的函数值之间有什么关系?反映在图像上,相应的两个点之间的位置又有关系??1.画出y=x2 与 y=x2 +2、 y=x2 -2的图像,并观察彼此的位置关系.试一试:6 3 2 3 62 -1 -2 -1 2y=x2y=x2 +2y=x2 -2函数y=x2的图象函数y=x2-2的图象函数y=x2+2的图象沿y轴向上平移2个单位长度沿y轴向下平移2个单位长度 函数y=ax2 (a≠0)和函数y=ax2+k (a≠0)的图象形状相同,只是位置不同:
(1)当k>0时,函数y=ax2+k的图象可由y=ax2的图象向上平移k个单位得到;
(2)当k<0时,函数y=ax2+k的图象可由y=ax2的图象向下平移|k|个单位得到。上加下减思考:比较函数y=ax2 (a≠0)和函数y=ax2+k (a≠0)的图象的异同,能总结出什么规律吗?小组研讨(0,0)(0,k)y轴y轴当x=0时,取最值0当x=0时,取最值ka>0,开口向上
a<0,开口向下相同抛物线顶点坐标对称轴开口方向增减性最值y=ax2 (a≠0)y=ax2+k (a≠0)相同a>0,开口向上
a<0,开口向下
3. 若y=x2+(2k-1)的顶点位于x轴上方,则K____ ___1、二次函数y=-x2-2是由二次函数y=-x2 向 平移 个单位得到的。 4. y =-2x2+5的图象可由抛物线y=-2x2经过 得到的. 它的对称轴是 , 顶点坐标是 ,在x<0时,y值随x的增大而 ;与x轴有 交点。沿Y轴向上平移5个单位Y轴(0,5)增大2 2.把函数y=3x2+2的图象沿x轴对折,得到的图象的函数解析为_______________.y=-3x2-2下2向上y轴( 0 , 5 )y轴y轴向下向下( 0 , -2 )( 0 , 3 )5. 填写下表: 6. 二次函数y=ax2+c (a≠0)的图象经过点A(1,-1),B(2,5),则函数y=ax2+c的表达式为 。若点C(-2,m),D(n ,7)也在函数的图象上,则点C的坐标为 ,点D的坐标为 .y=2x2-3(-2,5)7.函数y=ax2+a与y= (a≠0)在同一坐标系中 的大致图象是( )
yA.C.D.D? 解:以AB为x轴,对称轴为y轴建立直角坐标系,设抛物线的代数表达式为y=ax2+ c.?故0=24a+c,3=12a+c, ??其顶点为(0,6),(6-3)÷0.25=12小时.O向上向下(0 ,k)(0 ,k)y轴(直线x=0 )当x<0(在对称轴的左侧)时,
y随着x的增大而减小。
当x>0(在对称轴的右侧)时,
y随着x的增大而增大。 当x<0(在对称轴的左侧)时,
y随着x的增大而增大。
当x>0(在对称轴的右侧)时,
y随着x的增大而减小。 x=0时,y最小=kx=0时,y最大=k抛物线y=ax2 +k (a≠0)的图象可由y=ax2的图象通过上下平移得到(上加下减).y轴(直线x=0 )课本P10页习题26.2第1、2、3题。上21世纪教育网 下精品教学资源谢谢21世纪教育网(www.21cnjy.com)全国最大的中小学教育资源网站有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
最值不同增减性相同探索:观察下表思考这两个函数的图象的形状相同吗?提示:用平移的方法????2+10+1????2+1思考:自变量x取同一值时,两个函数的函数值之间有什么关系?反映在图像上,相应的两个点之间的位置又有关系??1.画出y=x2 与 y=x2 +2、 y=x2 -2的图像,并观察彼此的位置关系.试一试:6 3 2 3 62 -1 -2 -1 2y=x2y=x2 +2y=x2 -2函数y=x2的图象函数y=x2-2的图象函数y=x2+2的图象沿y轴向上平移2个单位长度沿y轴向下平移2个单位长度 函数y=ax2 (a≠0)和函数y=ax2+k (a≠0)的图象形状相同,只是位置不同:
(1)当k>0时,函数y=ax2+k的图象可由y=ax2的图象向上平移k个单位得到;
(2)当k<0时,函数y=ax2+k的图象可由y=ax2的图象向下平移|k|个单位得到。上加下减思考:比较函数y=ax2 (a≠0)和函数y=ax2+k (a≠0)的图象的异同,能总结出什么规律吗?小组研讨(0,0)(0,k)y轴y轴当x=0时,取最值0当x=0时,取最值ka>0,开口向上
a<0,开口向下相同抛物线顶点坐标对称轴开口方向增减性最值y=ax2 (a≠0)y=ax2+k (a≠0)相同a>0,开口向上
a<0,开口向下
3. 若y=x2+(2k-1)的顶点位于x轴上方,则K____ ___1、二次函数y=-x2-2是由二次函数y=-x2 向 平移 个单位得到的。 4. y =-2x2+5的图象可由抛物线y=-2x2经过 得到的. 它的对称轴是 , 顶点坐标是 ,在x<0时,y值随x的增大而 ;与x轴有 交点。沿Y轴向上平移5个单位Y轴(0,5)增大2 2.把函数y=3x2+2的图象沿x轴对折,得到的图象的函数解析为_______________.y=-3x2-2下2向上y轴( 0 , 5 )y轴y轴向下向下( 0 , -2 )( 0 , 3 )5. 填写下表: 6. 二次函数y=ax2+c (a≠0)的图象经过点A(1,-1),B(2,5),则函数y=ax2+c的表达式为 。若点C(-2,m),D(n ,7)也在函数的图象上,则点C的坐标为 ,点D的坐标为 .y=2x2-3(-2,5)7.函数y=ax2+a与y= (a≠0)在同一坐标系中 的大致图象是( )
yA.C.D.D? 解:以AB为x轴,对称轴为y轴建立直角坐标系,设抛物线的代数表达式为y=ax2+ c.?故0=24a+c,3=12a+c, ??其顶点为(0,6),(6-3)÷0.25=12小时.O向上向下(0 ,k)(0 ,k)y轴(直线x=0 )当x<0(在对称轴的左侧)时,
y随着x的增大而减小。
当x>0(在对称轴的右侧)时,
y随着x的增大而增大。 当x<0(在对称轴的左侧)时,
y随着x的增大而增大。
当x>0(在对称轴的右侧)时,
y随着x的增大而减小。 x=0时,y最小=kx=0时,y最大=k抛物线y=ax2 +k (a≠0)的图象可由y=ax2的图象通过上下平移得到(上加下减).y轴(直线x=0 )课本P10页习题26.2第1、2、3题。上21世纪教育网 下精品教学资源谢谢21世纪教育网(www.21cnjy.com)全国最大的中小学教育资源网站有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
