浙教版九年级数学下册培优练习:3.4 简单几何体的表面展开图(附答案)
文档属性
| 名称 | 浙教版九年级数学下册培优练习:3.4 简单几何体的表面展开图(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 599.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-21 14:19:40 | ||
图片预览


文档简介
3.4 简单几何体的表面展开图
一、选择题(共15小题)
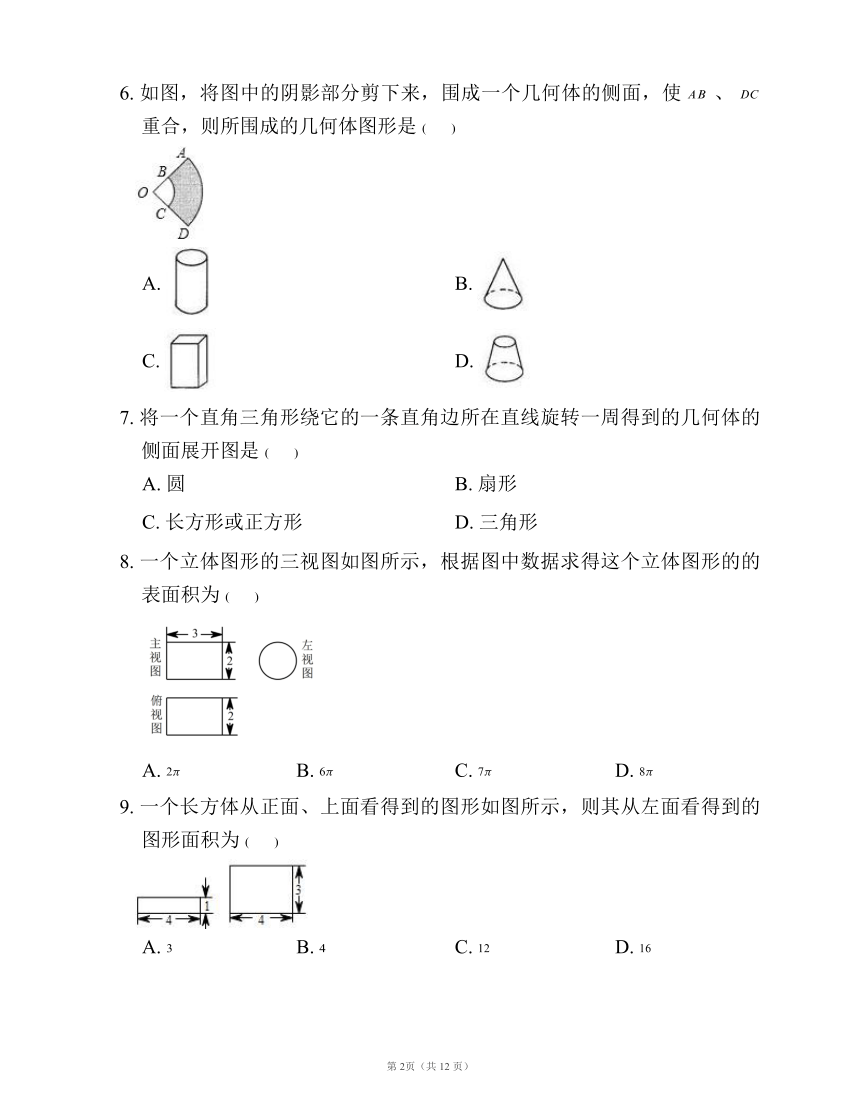
1. 一个几何体的展开图如图所示,则该几何体的顶点有
A. 个 B. 个 C. 个 D. 个
2. 下列各图中,经过折叠能围成一个立方体的是
A. B.
C. D.
3. 下列图形中,不是立方体表面展开图的是
A. B.
C. D.
4. 下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方形包装盒的是
A. B.
C. D.
5. 下列图形中只有一个面围成的是
A. 正方体 B. 圆柱 C. 圆锥 D. 球
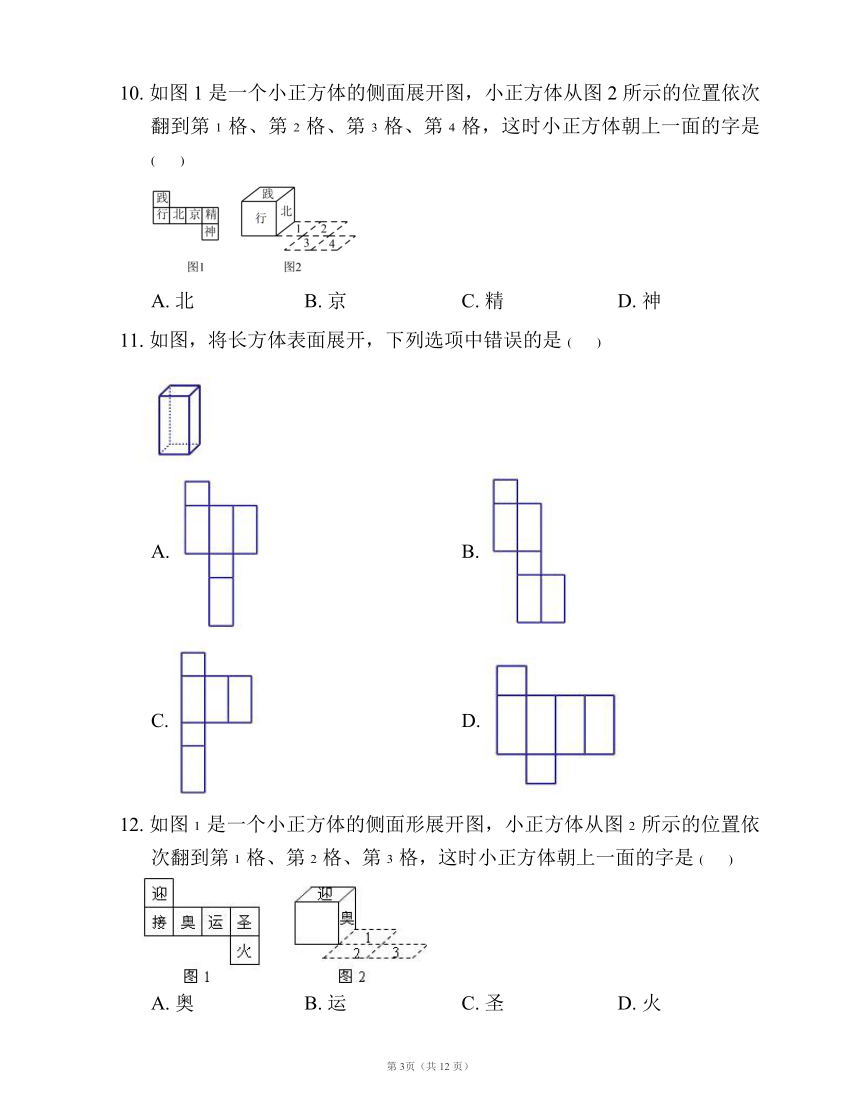
6. 如图,将图中的阴影部分剪下来,围成一个几何体的侧面,使 、 重合,则所围成的几何体图形是
A. B.
C. D.
7. 将一个直角三角形绕它的一条直角边所在直线旋转一周得到的几何体的侧面展开图是
A. 圆 B. 扇形
C. 长方形或正方形 D. 三角形
8. 一个立体图形的三视图如图所示,根据图中数据求得这个立体图形的的表面积为
A. B. C. D.
9. 一个长方体从正面、上面看得到的图形如图所示,则其从左面看得到的图形面积为
A. B. C. D.
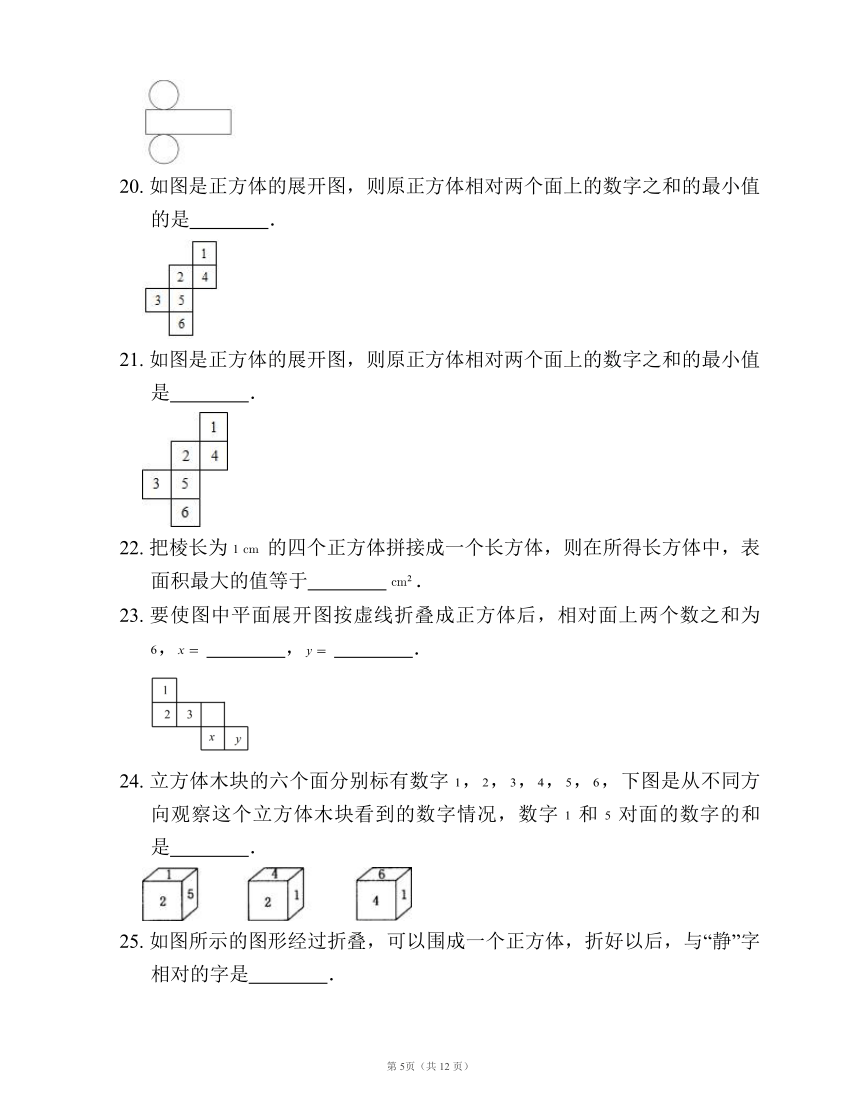
10. 如图 1 是一个小正方体的侧面展开图,小正方体从图 2 所示的位置依次翻到第 格、第 格、第 格、第 格,这时小正方体朝上一面的字是
A. 北 B. 京 C. 精 D. 神
11. 如图,将长方体表面展开,下列选项中错误的是
A. B.
C. D.
12. 如图 是一个小正方体的侧面形展开图,小正方体从图 所示的位置依次翻到第 格、第 格、第 格,这时小正方体朝上一面的字是
A. 奥 B. 运 C. 圣 D. 火
13. 将一边长为 的正方形纸片折成四部分,再沿折痕折起来,恰好能不重叠地搭建成一个三棱锥,则此三棱锥四个面中最小的面积是
A. B. C. D.
14. 如图所示是老年活动中心门口放着的一个招牌,这个招牌是由三个特大号的骰子摞在一起而成的.每个骰子的六个面的点数分别是 到 .其中可看见 个面,其余 个面是看不见的,则看不见的面上的点数总和是
A. B. C. D.
15. 将一边长为 的正方形纸片折成四部分,再沿折痕折起来,恰好能不重叠地搭建成一个三棱锥,则三棱锥四个面中最小的面积是
A. B. C. D.
二、填空题(共15小题)
16. 如图所示,将图沿实线折起来得到一个正方体,那么“”的对面是 ?(填编号).
17. 直三棱柱底面边长都是 ,侧棱长为 ,则侧面展开图的面积是 ?.
18. 圆柱的底面周长为 ,高为 ,则圆柱的侧面展开图的面积为 ?.
19. 若图是某几何体的表面展开图,则这个几何体是 ?.
20. 如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值的是 ?.
21. 如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是 ?.
22. 把棱长为 的四个正方体拼接成一个长方体,则在所得长方体中,表面积最大的值等于 ? .
23. 要使图中平面展开图按虚线折叠成正方体后,相对面上两个数之和为 , ?, ?.
24. 立方体木块的六个面分别标有数字 ,,,,,,下图是从不同方向观察这个立方体木块看到的数字情况,数字 和 对面的数字的和是 ?.
25. 如图所示的图形经过折叠,可以围成一个正方体,折好以后,与“静”字相对的字是 ?.
26. 如图所示图形可以折成一个正方体形状的盒子,折好后,与“做”字相对应的字是 ?.
27. 有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动 算一次,则滚动第 次后,骰子朝下一面的点数是 ?.
28. 如图所示,要使展开图按虚线折叠成正方体后,相对面上两个数之积为 ,则 ?.
29. 马小虎准备制作一个封闭的正方体盒子,他先用 个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在右图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子(添加所有符合要求的正方形,添加的正方形用阴影表示) ?.
30. 将正方体骰子(相对面上的点数分别为 和 , 和 , 和 )放置于水平桌面上,如图 1.在图 2 中,将骰子向右翻滚 ,然后在桌面上按逆时针方向旋转 ,则完成一次变换.若骰子的初始位置为图 1 所示的状态,那么按上述规则连续完成 次变换后,骰子朝上一面的点数是 ?;连续完成 次变换后,骰子朝上一面的点数是 ?.
三、解答题(共5小题)
31. 如图所示是一个食品包装盒的侧面展开图.
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标的尺寸,计算这个多面体的侧面积和全面积(侧面积与两个底面体之和).
32. 请根据图①②所示的数字,在图③中的空格中填上相应的数字.
33. 如图,有一个正方体的盒子 ,在盒子的顶点 处有一只蚂蚁,而在对角的顶点 处有一块糖,蚂蚁应沿着什么路径爬行,才能最快地吃到糖,请画出蚂蚁爬行的路线并简要说明理由.
34. 如图 所示,一个长方体的长、宽、高分别是 ,,,有一只蚂蚁从点 出发沿棱爬行,每条棱不允许重复,则蚂蚁回到点 时,最多爬行多远?并把蚂蚁所爬行的路线用字母按顺序表示出来.
35. 如图所示是一个底面为正方形的长方体,把它的侧面展开后,恰好是一个边长为 的正方形,求这个长方体的体积.
答案
1. C
2. A
3. C
4. C
5. D
6. D
7. B
8. D 【解析】根据三视图得到该立体图形为圆柱,再由圆柱的展开图是一个矩形和两个圆,根据题目中的数据,求出表面积.
9. A 【解析】从正面和上面看可知长方体的长为 ,宽为 ,高为 ,
所以它从左面看所得长方形的面积等于 .
10. A
【解析】由图1可得,“践”和“神”相对;“北”和“精”相对;“行”和“京”相对;
由图2可得,小正方体从图2的位置依次翻到第4格时,“精”在下面,则这时小正方体朝上面的字是“北”.
11. C
12. D
13. C 【解析】
取正方形相邻两边的中点,如图.
三棱锥四个面中的最小的一个面是等腰直角三角形,它的两条直角边等于正方形边长的一半,
根据三角形面积公式可得最小面积为 .
14. C 【解析】看见的 个面上的点数之和为 ,所以看不见的 个面的点数之和为 .
15. C
【解析】
如图所示,最小的一个面是等腰直角三角形,面积是 .
16.
17.
18.
19. 圆柱
20.
21.
22.
【解析】排成一列时,面积最大重合的有个 面.
23. ,
24.
【解析】由图可知和 相邻的数字有 ,,,,
所以 对面的数字是 ,
而 不和 , 相对,
所以 的对面是 ,
所以 .
25. 着
26. 人
27.
【解析】观察图象知道点数三和点数四相对,点数二和点数五相对且四次一循环,
,
滚动第 次后与第二次相同,
朝下的点数为 .
28. 0
【解析】将题图中展开图按虚线折叠成正方体后,可知标有数字" "的面和标有" "的面是相对面,标有数字" "的面和标有" "的面是相对面,
所以 ,,
所以 .
29.
30. ,
【解析】第 次变换:
第 次变换:
第 次变换:
易得,每 次变换为一个周期,而 ,
所以连续完成 次变换后,骰子朝上一面的点数是 .
31. (1) 这个多面体是六棱柱.
??????(2) 侧面积为 ;
全面积为 .
32. 对面是 , 对面是 ( 在 与 之间), 对面是 .
【解析】可以自己用纸剪一个试试看.
33. 经过六种途径可以最快到达,分别取 ,,,,, 的中点 ,,,,,,六条途径分别为 ,,,,,,如图所示,将蚂蚁所在的起始点与终点的平面展开,连接两个目标点,即得到最近线路.
34. 由于不能重复且最后回到点 处,那么经过的棱数便等于经过的顶点数,当走的路线最长时必过所有顶点,则选择合理的路线时尽可能多地经过长为 的棱即可.
,
所以最多爬行 .
路线举例:.
35.
答:这个长方体的体积是 .
一、选择题(共15小题)
1. 一个几何体的展开图如图所示,则该几何体的顶点有
A. 个 B. 个 C. 个 D. 个
2. 下列各图中,经过折叠能围成一个立方体的是
A. B.
C. D.
3. 下列图形中,不是立方体表面展开图的是
A. B.
C. D.
4. 下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方形包装盒的是
A. B.
C. D.
5. 下列图形中只有一个面围成的是
A. 正方体 B. 圆柱 C. 圆锥 D. 球
6. 如图,将图中的阴影部分剪下来,围成一个几何体的侧面,使 、 重合,则所围成的几何体图形是
A. B.
C. D.
7. 将一个直角三角形绕它的一条直角边所在直线旋转一周得到的几何体的侧面展开图是
A. 圆 B. 扇形
C. 长方形或正方形 D. 三角形
8. 一个立体图形的三视图如图所示,根据图中数据求得这个立体图形的的表面积为
A. B. C. D.
9. 一个长方体从正面、上面看得到的图形如图所示,则其从左面看得到的图形面积为
A. B. C. D.
10. 如图 1 是一个小正方体的侧面展开图,小正方体从图 2 所示的位置依次翻到第 格、第 格、第 格、第 格,这时小正方体朝上一面的字是
A. 北 B. 京 C. 精 D. 神
11. 如图,将长方体表面展开,下列选项中错误的是
A. B.
C. D.
12. 如图 是一个小正方体的侧面形展开图,小正方体从图 所示的位置依次翻到第 格、第 格、第 格,这时小正方体朝上一面的字是
A. 奥 B. 运 C. 圣 D. 火
13. 将一边长为 的正方形纸片折成四部分,再沿折痕折起来,恰好能不重叠地搭建成一个三棱锥,则此三棱锥四个面中最小的面积是
A. B. C. D.
14. 如图所示是老年活动中心门口放着的一个招牌,这个招牌是由三个特大号的骰子摞在一起而成的.每个骰子的六个面的点数分别是 到 .其中可看见 个面,其余 个面是看不见的,则看不见的面上的点数总和是
A. B. C. D.
15. 将一边长为 的正方形纸片折成四部分,再沿折痕折起来,恰好能不重叠地搭建成一个三棱锥,则三棱锥四个面中最小的面积是
A. B. C. D.
二、填空题(共15小题)
16. 如图所示,将图沿实线折起来得到一个正方体,那么“”的对面是 ?(填编号).
17. 直三棱柱底面边长都是 ,侧棱长为 ,则侧面展开图的面积是 ?.
18. 圆柱的底面周长为 ,高为 ,则圆柱的侧面展开图的面积为 ?.
19. 若图是某几何体的表面展开图,则这个几何体是 ?.
20. 如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值的是 ?.
21. 如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是 ?.
22. 把棱长为 的四个正方体拼接成一个长方体,则在所得长方体中,表面积最大的值等于 ? .
23. 要使图中平面展开图按虚线折叠成正方体后,相对面上两个数之和为 , ?, ?.
24. 立方体木块的六个面分别标有数字 ,,,,,,下图是从不同方向观察这个立方体木块看到的数字情况,数字 和 对面的数字的和是 ?.
25. 如图所示的图形经过折叠,可以围成一个正方体,折好以后,与“静”字相对的字是 ?.
26. 如图所示图形可以折成一个正方体形状的盒子,折好后,与“做”字相对应的字是 ?.
27. 有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动 算一次,则滚动第 次后,骰子朝下一面的点数是 ?.
28. 如图所示,要使展开图按虚线折叠成正方体后,相对面上两个数之积为 ,则 ?.
29. 马小虎准备制作一个封闭的正方体盒子,他先用 个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在右图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子(添加所有符合要求的正方形,添加的正方形用阴影表示) ?.
30. 将正方体骰子(相对面上的点数分别为 和 , 和 , 和 )放置于水平桌面上,如图 1.在图 2 中,将骰子向右翻滚 ,然后在桌面上按逆时针方向旋转 ,则完成一次变换.若骰子的初始位置为图 1 所示的状态,那么按上述规则连续完成 次变换后,骰子朝上一面的点数是 ?;连续完成 次变换后,骰子朝上一面的点数是 ?.
三、解答题(共5小题)
31. 如图所示是一个食品包装盒的侧面展开图.
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标的尺寸,计算这个多面体的侧面积和全面积(侧面积与两个底面体之和).
32. 请根据图①②所示的数字,在图③中的空格中填上相应的数字.
33. 如图,有一个正方体的盒子 ,在盒子的顶点 处有一只蚂蚁,而在对角的顶点 处有一块糖,蚂蚁应沿着什么路径爬行,才能最快地吃到糖,请画出蚂蚁爬行的路线并简要说明理由.
34. 如图 所示,一个长方体的长、宽、高分别是 ,,,有一只蚂蚁从点 出发沿棱爬行,每条棱不允许重复,则蚂蚁回到点 时,最多爬行多远?并把蚂蚁所爬行的路线用字母按顺序表示出来.
35. 如图所示是一个底面为正方形的长方体,把它的侧面展开后,恰好是一个边长为 的正方形,求这个长方体的体积.
答案
1. C
2. A
3. C
4. C
5. D
6. D
7. B
8. D 【解析】根据三视图得到该立体图形为圆柱,再由圆柱的展开图是一个矩形和两个圆,根据题目中的数据,求出表面积.
9. A 【解析】从正面和上面看可知长方体的长为 ,宽为 ,高为 ,
所以它从左面看所得长方形的面积等于 .
10. A
【解析】由图1可得,“践”和“神”相对;“北”和“精”相对;“行”和“京”相对;
由图2可得,小正方体从图2的位置依次翻到第4格时,“精”在下面,则这时小正方体朝上面的字是“北”.
11. C
12. D
13. C 【解析】
取正方形相邻两边的中点,如图.
三棱锥四个面中的最小的一个面是等腰直角三角形,它的两条直角边等于正方形边长的一半,
根据三角形面积公式可得最小面积为 .
14. C 【解析】看见的 个面上的点数之和为 ,所以看不见的 个面的点数之和为 .
15. C
【解析】
如图所示,最小的一个面是等腰直角三角形,面积是 .
16.
17.
18.
19. 圆柱
20.
21.
22.
【解析】排成一列时,面积最大重合的有个 面.
23. ,
24.
【解析】由图可知和 相邻的数字有 ,,,,
所以 对面的数字是 ,
而 不和 , 相对,
所以 的对面是 ,
所以 .
25. 着
26. 人
27.
【解析】观察图象知道点数三和点数四相对,点数二和点数五相对且四次一循环,
,
滚动第 次后与第二次相同,
朝下的点数为 .
28. 0
【解析】将题图中展开图按虚线折叠成正方体后,可知标有数字" "的面和标有" "的面是相对面,标有数字" "的面和标有" "的面是相对面,
所以 ,,
所以 .
29.
30. ,
【解析】第 次变换:
第 次变换:
第 次变换:
易得,每 次变换为一个周期,而 ,
所以连续完成 次变换后,骰子朝上一面的点数是 .
31. (1) 这个多面体是六棱柱.
??????(2) 侧面积为 ;
全面积为 .
32. 对面是 , 对面是 ( 在 与 之间), 对面是 .
【解析】可以自己用纸剪一个试试看.
33. 经过六种途径可以最快到达,分别取 ,,,,, 的中点 ,,,,,,六条途径分别为 ,,,,,,如图所示,将蚂蚁所在的起始点与终点的平面展开,连接两个目标点,即得到最近线路.
34. 由于不能重复且最后回到点 处,那么经过的棱数便等于经过的顶点数,当走的路线最长时必过所有顶点,则选择合理的路线时尽可能多地经过长为 的棱即可.
,
所以最多爬行 .
路线举例:.
35.
答:这个长方体的体积是 .
