浙教版九年级数学下册培优练习:2.1 直线与圆的位置关系(附答案)
文档属性
| 名称 | 浙教版九年级数学下册培优练习:2.1 直线与圆的位置关系(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-21 14:23:03 | ||
图片预览




文档简介
2.1 直线与圆的位置关系
一、选择题(共15小题)
1. 如图, 中,,,,以点 为圆心的圆与 相切,则 的半径为
A. B. C. D.
2. 已知圆的半径为 ,如果一条直线和圆心的距离为 ,那么这条直线和这个圆的位置关系是
A. 相交 B. 相切 C. 相离 D. 相交或相离
3. 如图, 是 的弦, 与 相切于点 ,连接 、 .若 ,则 等于
A. B. C. D.
4. 在平面直角坐标系 中,以 为圆心,半径为 的圆与 轴的位置关系是
A. 相离 B. 相交 C. 相切 D. 无法确定
5. 如图,已知线段 交 于点 ,且 ,点 是 上的一个动点,那么 的最大值是
A. B. C. D.
6. 以点 为圆心, 为半径画圆,与坐标轴恰好有三个交点,则 应满足
A. 或 B. C. D.
7. 若等腰直角三角形的外接圆半径的长为 ,则其内切圆半径的长为
A. B. C. D.
8. 和 的半径分别是 和 ,如果 ,则这两圆的位置关系是
A. 内含 B. 相交 C. 外切 D. 外离
9. 如图所示, 切 于 , 交 于 ,若 ,,则 的半径是
A. B. C. D.
10. 如图, 与 相切于点 , 的延长线交 于点 ,连接 ,若 ,则 等于
A. B. C. D.
11. 如图, 的半径是 ,点 是弦 延长线上的一点,连接 ,若 ,,则弦 的长为
A. B. C. D.
12. 如果正三角形的内切圆半径为 ,那么这个正三角形的边长为
A. B. C. D.
13. 如图, 是 的切线, 为切点, 的延长线交 于 点,连接 ,若 ,,则 等于
A. B. C. D.
14. 在平面直角坐标系 中,点 的坐标为 .如果以原点为圆心,半径为 的 上存在点 ,使得 ,那么 的取值范围是
A. B. C. D.
15. 如图所示, 为 的直径, 切 于点 ,交 的延长线于 ,且 ,则
A. B. C. D.
二、填空题(共15小题)
16. 如图, 切 于 ,,则 ?.
17. 已知 的半径为 ,点 是 外一点, 的长为 ,那么以 为圆心,且与 相切的圆的半径是 ?.
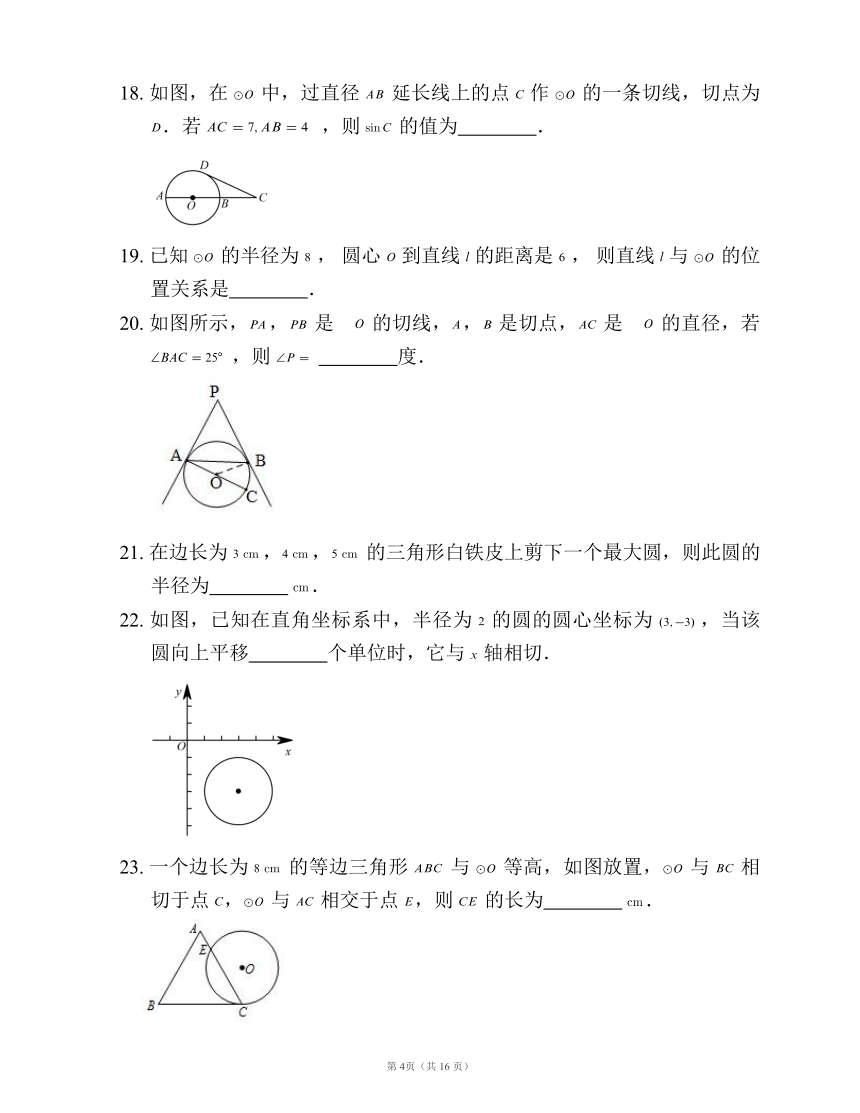
18. 如图,在 中,过直径 延长线上的点 作 的一条切线,切点为 .若 ,则 的值为 ?.
19. 已知 的半径为 , 圆心 到直线 的距离是 , 则直线 与 的位置关系是 ?.
20. 如图所示,, 是 的切线,, 是切点, 是 的直径,若 ,则 ?度.
21. 在边长为 ,, 的三角形白铁皮上剪下一个最大圆,则此圆的半径为 ? .
22. 如图,已知在直角坐标系中,半径为 的圆的圆心坐标为 ,当该圆向上平移 ?个单位时,它与 轴相切.
23. 一个边长为 的等边三角形 与 等高,如图放置, 与 相切于点 , 与 相交于点 ,则 的长为 ? .
24. 在 中,,, ,则 的内切圆的半径为 ?
25. 已知 ,点 在 的平分线上,,以 为圆心 为半径作圆,则圆 与 的位置关系是 ?.
26. 如图所示,在 中,点 是 的内心,则 ? 度.
27. 如图所示, 是 外一点,, 分别切 于点 , 切 于点 ,分别交 , 于点 ,.若 ,则 的周长为 ?.
28. 已知:如图, 是 的内切圆,分别切 ,, 于 ,,, 的周长为 ,,则 ? .
29. 如图所示,, 是 的切线, 是 的直径,,则 ?.
30. 如图,点 ,, 分别在正三角形 的三边上,且 也是正三角形,若 的边长为 , 的边长为 ,则 的内切圆半径为 ?.
三、解答题(共5小题)
31. 任何三角形都有一个内切圆,任何四边形是否一定有一个内切圆?请举例说明.
32. 定义:对于数轴上的任意两点 , 分别表示数 ,,用 表示它们之间的距离;对于平面直角坐标系中的任意两点 ,,我们把 叫做 , 两点之间的直角距离,记作 .
(1)已知 为坐标原点,若点 坐标为 ,则 ?;
(2)已知 是直线 上的一个动点,
(i)若 ,求点 与点 的直角距离的最小值;
(ii)若 是以原点 为圆心, 为半径的圆上的一个动点,请直接写出点 与点 的直角距离的最小值.
33. 已知:如图,在 中,, 是 边上一点,以 为直径作 恰过点 .
(1)求证: 所在直线是 的切线;
(2)若 ,求弦 的长.
34. 如图, 为 的直径,以 为直角边作 ,,斜边 与 交于点 ,过点 作 的切线 交 于点 , 于点 ,交 于点 .
(1)求证:;
(2)若 ,,求 的长.
35. 已知:如图, 为 的直径,, 是 的切线, 、 为切点,.
(1)求 的大小;
(2)若 ,求 的长.
答案
1. B 【解析】答案:B
2. C
3. B
4. B
5. D
6. A 【解析】如图是圆心为 ,半径分别为 和 时的圆与坐标轴有三个交点时的情况.
7. B 【解析】,,用面积可得 ,.
8. C
9. C 【解析】 切 于 ,
.
设圆的半径为 ,
由勾股定理得,,解得 .
10. B
【解析】
连接 ,则 ,,
,
.
11. A 【解析】过 作 于点 ,连接 .
,,
,
,
,
.
12. B
13. B 【解析】
连接 ,则 .
在 中,,.
,.
.
14. A 【解析】如图所示,当直线 与 相切时,若 ,满足题意,故 .
15. D
【解析】 切 于点 ,
.
又 ,
.
,
,
.
16.
17. 或
18.
19. 相交
20.
【解析】,
.
21.
【解析】由勾股定理的逆定理可得,边长为 ,, 的三角形是直角三角形,其内切圆半径 ().
22. 或
23.
【解析】提示:连接(OE),,.
的直径为 ,,.
24.
25. 相交
【解析】提示:点 到 的距离为 ,半径为 ,
,
圆 与 相交.
26.
【解析】由点 是 的内心,得 平分 , 平分 , 平分 ,所以
27.
【解析】由切线长定理,
得
.
28.
【解析】 是 的内切圆,分别切 ,, 于点 ,,,
设 ,,.
根据题意得:,
解得 .
.
29.
【解析】, 是 的切线,
(切线长定理),(切线性质定理),
,
.
30.
【解析】
如图,由于 , 都为正三角形,
,,,
,
.
在 和 中,
.
同理可证:.
,即 .
设 是 的内心,作 于 , 于 , 于 ,则 ,,,
则 .
平分 , .
设 ,则 ,根据勾股定理,得 ,解得 .
故 的内切圆半径为 .
31. 四边形不一定有内切圆,如长为 ,宽为 的矩形没有内切圆.
32. (1)
??????(2) (i)设 的坐标为 ,则 .
当 时,;
当 时,;
当 时,.
所以 .
(ii).
【解析】过 作 垂直于直线 ,交圆于点 ,交直线于 ,此时可求点 与点 的直角距离的最小值.
点 ,点 .
33. (1) 如图,连接 .
则 ,.
在 中,
,
.
.
.
是 的切线.
??????(2) 连接 .
是 的直径,
.
在 中,
,,
.
即弦 的长为 .
34. (1) 连接 ,
为 的直径,,
是 的切线.
与 相切,
.
.
是 的直径,
.
,
,
,
.
??????(2) ,
.
在 中,.
.
,
,
,
.
于点 ,
.
35. (1) 是 的切线, 为 的直径,
.
,
,
.
, 切 于点 ,,
,
是等边三角形,
.
??????(2) 如图,连接 .
是直径, ,
在 中,,,
.
又 是等边三角形,
.
一、选择题(共15小题)
1. 如图, 中,,,,以点 为圆心的圆与 相切,则 的半径为
A. B. C. D.
2. 已知圆的半径为 ,如果一条直线和圆心的距离为 ,那么这条直线和这个圆的位置关系是
A. 相交 B. 相切 C. 相离 D. 相交或相离
3. 如图, 是 的弦, 与 相切于点 ,连接 、 .若 ,则 等于
A. B. C. D.
4. 在平面直角坐标系 中,以 为圆心,半径为 的圆与 轴的位置关系是
A. 相离 B. 相交 C. 相切 D. 无法确定
5. 如图,已知线段 交 于点 ,且 ,点 是 上的一个动点,那么 的最大值是
A. B. C. D.
6. 以点 为圆心, 为半径画圆,与坐标轴恰好有三个交点,则 应满足
A. 或 B. C. D.
7. 若等腰直角三角形的外接圆半径的长为 ,则其内切圆半径的长为
A. B. C. D.
8. 和 的半径分别是 和 ,如果 ,则这两圆的位置关系是
A. 内含 B. 相交 C. 外切 D. 外离
9. 如图所示, 切 于 , 交 于 ,若 ,,则 的半径是
A. B. C. D.
10. 如图, 与 相切于点 , 的延长线交 于点 ,连接 ,若 ,则 等于
A. B. C. D.
11. 如图, 的半径是 ,点 是弦 延长线上的一点,连接 ,若 ,,则弦 的长为
A. B. C. D.
12. 如果正三角形的内切圆半径为 ,那么这个正三角形的边长为
A. B. C. D.
13. 如图, 是 的切线, 为切点, 的延长线交 于 点,连接 ,若 ,,则 等于
A. B. C. D.
14. 在平面直角坐标系 中,点 的坐标为 .如果以原点为圆心,半径为 的 上存在点 ,使得 ,那么 的取值范围是
A. B. C. D.
15. 如图所示, 为 的直径, 切 于点 ,交 的延长线于 ,且 ,则
A. B. C. D.
二、填空题(共15小题)
16. 如图, 切 于 ,,则 ?.
17. 已知 的半径为 ,点 是 外一点, 的长为 ,那么以 为圆心,且与 相切的圆的半径是 ?.
18. 如图,在 中,过直径 延长线上的点 作 的一条切线,切点为 .若 ,则 的值为 ?.
19. 已知 的半径为 , 圆心 到直线 的距离是 , 则直线 与 的位置关系是 ?.
20. 如图所示,, 是 的切线,, 是切点, 是 的直径,若 ,则 ?度.
21. 在边长为 ,, 的三角形白铁皮上剪下一个最大圆,则此圆的半径为 ? .
22. 如图,已知在直角坐标系中,半径为 的圆的圆心坐标为 ,当该圆向上平移 ?个单位时,它与 轴相切.
23. 一个边长为 的等边三角形 与 等高,如图放置, 与 相切于点 , 与 相交于点 ,则 的长为 ? .
24. 在 中,,, ,则 的内切圆的半径为 ?
25. 已知 ,点 在 的平分线上,,以 为圆心 为半径作圆,则圆 与 的位置关系是 ?.
26. 如图所示,在 中,点 是 的内心,则 ? 度.
27. 如图所示, 是 外一点,, 分别切 于点 , 切 于点 ,分别交 , 于点 ,.若 ,则 的周长为 ?.
28. 已知:如图, 是 的内切圆,分别切 ,, 于 ,,, 的周长为 ,,则 ? .
29. 如图所示,, 是 的切线, 是 的直径,,则 ?.
30. 如图,点 ,, 分别在正三角形 的三边上,且 也是正三角形,若 的边长为 , 的边长为 ,则 的内切圆半径为 ?.
三、解答题(共5小题)
31. 任何三角形都有一个内切圆,任何四边形是否一定有一个内切圆?请举例说明.
32. 定义:对于数轴上的任意两点 , 分别表示数 ,,用 表示它们之间的距离;对于平面直角坐标系中的任意两点 ,,我们把 叫做 , 两点之间的直角距离,记作 .
(1)已知 为坐标原点,若点 坐标为 ,则 ?;
(2)已知 是直线 上的一个动点,
(i)若 ,求点 与点 的直角距离的最小值;
(ii)若 是以原点 为圆心, 为半径的圆上的一个动点,请直接写出点 与点 的直角距离的最小值.
33. 已知:如图,在 中,, 是 边上一点,以 为直径作 恰过点 .
(1)求证: 所在直线是 的切线;
(2)若 ,求弦 的长.
34. 如图, 为 的直径,以 为直角边作 ,,斜边 与 交于点 ,过点 作 的切线 交 于点 , 于点 ,交 于点 .
(1)求证:;
(2)若 ,,求 的长.
35. 已知:如图, 为 的直径,, 是 的切线, 、 为切点,.
(1)求 的大小;
(2)若 ,求 的长.
答案
1. B 【解析】答案:B
2. C
3. B
4. B
5. D
6. A 【解析】如图是圆心为 ,半径分别为 和 时的圆与坐标轴有三个交点时的情况.
7. B 【解析】,,用面积可得 ,.
8. C
9. C 【解析】 切 于 ,
.
设圆的半径为 ,
由勾股定理得,,解得 .
10. B
【解析】
连接 ,则 ,,
,
.
11. A 【解析】过 作 于点 ,连接 .
,,
,
,
,
.
12. B
13. B 【解析】
连接 ,则 .
在 中,,.
,.
.
14. A 【解析】如图所示,当直线 与 相切时,若 ,满足题意,故 .
15. D
【解析】 切 于点 ,
.
又 ,
.
,
,
.
16.
17. 或
18.
19. 相交
20.
【解析】,
.
21.
【解析】由勾股定理的逆定理可得,边长为 ,, 的三角形是直角三角形,其内切圆半径 ().
22. 或
23.
【解析】提示:连接(OE),,.
的直径为 ,,.
24.
25. 相交
【解析】提示:点 到 的距离为 ,半径为 ,
,
圆 与 相交.
26.
【解析】由点 是 的内心,得 平分 , 平分 , 平分 ,所以
27.
【解析】由切线长定理,
得
.
28.
【解析】 是 的内切圆,分别切 ,, 于点 ,,,
设 ,,.
根据题意得:,
解得 .
.
29.
【解析】, 是 的切线,
(切线长定理),(切线性质定理),
,
.
30.
【解析】
如图,由于 , 都为正三角形,
,,,
,
.
在 和 中,
.
同理可证:.
,即 .
设 是 的内心,作 于 , 于 , 于 ,则 ,,,
则 .
平分 , .
设 ,则 ,根据勾股定理,得 ,解得 .
故 的内切圆半径为 .
31. 四边形不一定有内切圆,如长为 ,宽为 的矩形没有内切圆.
32. (1)
??????(2) (i)设 的坐标为 ,则 .
当 时,;
当 时,;
当 时,.
所以 .
(ii).
【解析】过 作 垂直于直线 ,交圆于点 ,交直线于 ,此时可求点 与点 的直角距离的最小值.
点 ,点 .
33. (1) 如图,连接 .
则 ,.
在 中,
,
.
.
.
是 的切线.
??????(2) 连接 .
是 的直径,
.
在 中,
,,
.
即弦 的长为 .
34. (1) 连接 ,
为 的直径,,
是 的切线.
与 相切,
.
.
是 的直径,
.
,
,
,
.
??????(2) ,
.
在 中,.
.
,
,
,
.
于点 ,
.
35. (1) 是 的切线, 为 的直径,
.
,
,
.
, 切 于点 ,,
,
是等边三角形,
.
??????(2) 如图,连接 .
是直径, ,
在 中,,,
.
又 是等边三角形,
.
