浙教版九年级有关切线问题的辅助线作法专题(含答案)
文档属性
| 名称 | 浙教版九年级有关切线问题的辅助线作法专题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 508.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-28 16:36:16 | ||
图片预览



文档简介
有关切线问题的辅助线作法
一、切线的性质
(教材P44作业题第5题)
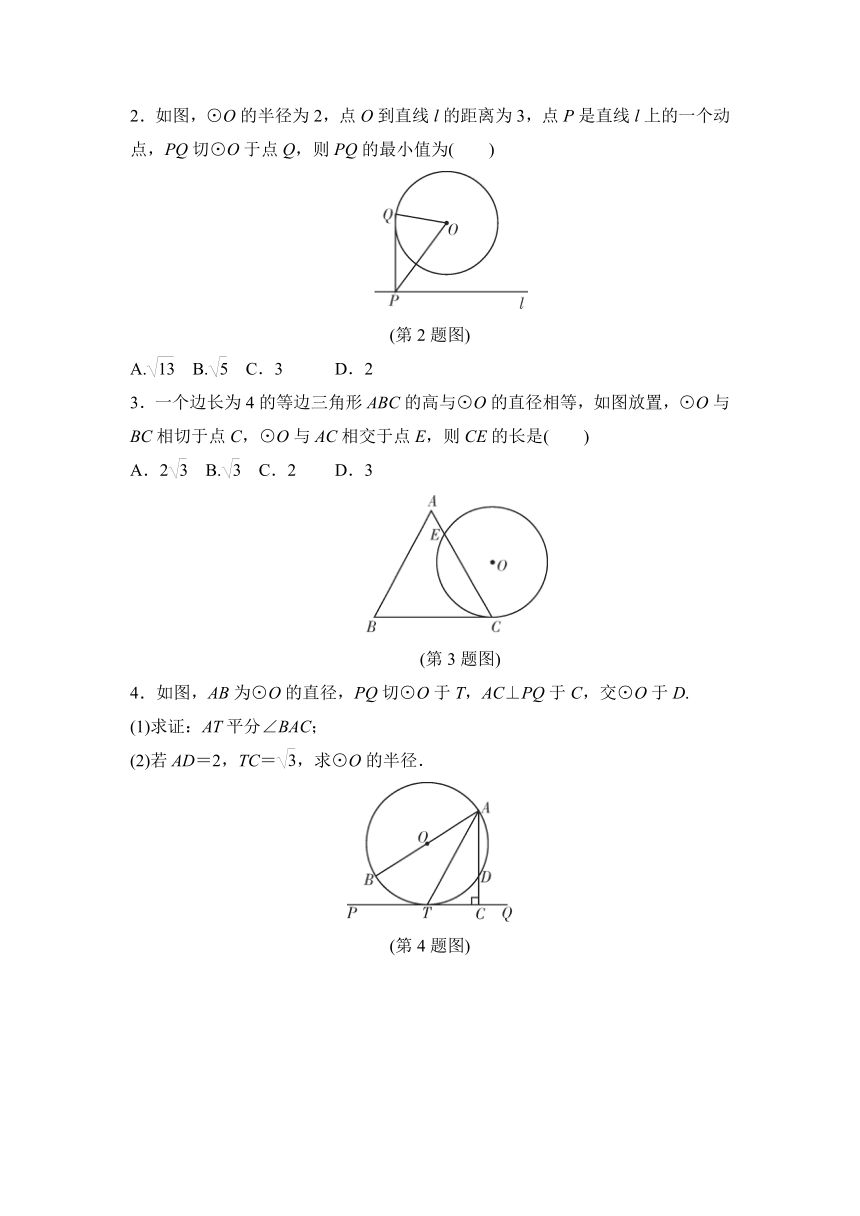
如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于F点,已知AC=12,BC=9,求AO的长.
(教材母题图) 教材母题答图
解:连结OE,如答图所示:
∵BC⊥AC于点C,∴∠C=90°,
在Rt△ABC中,AC=12,BC=9,根据勾股定理得AB=15,
∵AC切半圆于点E,∴OE⊥AC,
∴OE∥BC,∴=,
设OE为x,则AO为15-x,
∴=,解得x=,
则AO=AB-BO=15-=.
与切线有关的长度计算
1.如图,已知⊙O过正方形ABCD的顶点A,B,且与CD边相切,若正方形的边长为2,则圆的半径为( )
A. B. C. D.1
(第1 题图)
2.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
(第2题图)
A. B. C.3 D.2
3.一个边长为4的等边三角形ABC的高与⊙O的直径相等,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长是( )
A.2 B. C.2 D.3
(第3题图)
4.如图,AB为⊙O的直径,PQ切⊙O于T,AC⊥PQ于C,交⊙O于D.
(1)求证:AT平分∠BAC;
(2)若AD=2,TC=,求⊙O的半径.
(第4题图)
5.如图,在Rt△ABC中,∠B=90°,E为AB上一点,O是BC上一点,∠C=∠BEO,以O为圆心,OB长为半径作⊙O,AC是⊙O的切线.
(1)求证:OE=OC;
(2)若BE=4,BC=8,求OE的长.
(第5题图)
6.△ABC内接于⊙O,BC是⊙O的直径.
(1)过点B的切线与OA的延长线交于点P,如图1,若∠C=∠ABC,AB=2,求切线BP的长;
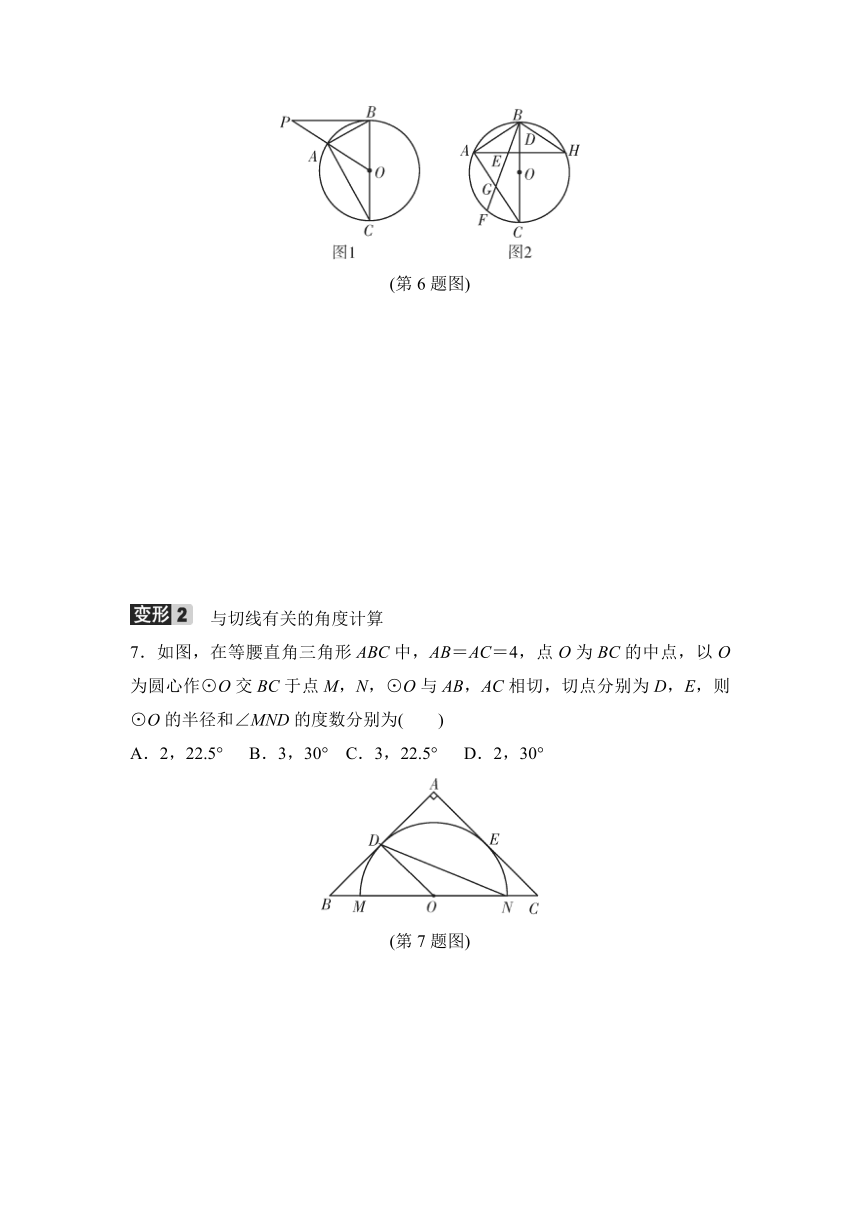
(2)过点A作AD⊥BC于D,交⊙O于H,过点B作弦BF交AD于E,交⊙O于F,且AE=BE,如图2.求证:=.
(第6题图)
与切线有关的角度计算
7.如图,在等腰直角三角形ABC中,AB=AC=4,点O为BC的中点,以O为圆心作⊙O交BC于点M,N,⊙O与AB,AC相切,切点分别为D,E,则⊙O的半径和∠MND的度数分别为( )
A.2,22.5° B.3,30° C.3,22.5° D.2,30°
(第7题图)
8.如图,已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D,则∠CDP等于( )
A.30° B.60° C.45° D.50°
(第8题图)
9.如图,已知,PD为⊙O的直径,直线BC切⊙O于点C,BP的延长线与CD的延长线交于点A,∠A=28°,∠B=26°,则∠PDC等于( )
A.34° B.36° C.38° D.40°
(第9题图)
10.如图,四边形ABCD内接于⊙O,AB为直径,PD切⊙O于D,与BA延长线交于P点,已知∠C=130°,则∠ADP=____.
(第10题图)
11.如图,已知⊙O上有A,B,C三点,D是OB延长线上的点,∠BDC=30°,CD是⊙O的切线,⊙O的半径为.
(1)求∠A的度数;
(2)如果AC∥BD,请判断四边形ACDB是什么四边形,并求其周长.
( 第11题图)
12.已知⊙O中,AC为直径,MA,MB分别切⊙O于点A,B.
(1)如图1,若∠BAC=25°,求∠M的大小;
(2)如图2,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,求∠M的大小.
(第12题图)
二、切线的判定
(教材P44练习题第4题)
已知,如图,PA是⊙O的切线,A是切点,B为⊙O上的一点,PA=PB.求证:PB是⊙O切线.
(教材母题图) 教材母题答图
证明:连结OA,OB,OP,如答图,
在△AOP和△BOP中,
∴△AOP≌△BOP,∵OA⊥AP,
∴OB⊥BP,即PB是⊙O的切线.
【思想方法】证明某直线为圆的切线时,如果该直线与已知圆有公共点,即可作出经过该点的半径,证明直线垂直于该半径,即“连半径,证垂直”;如果不能确定该直线与已知圆有公共点,则过圆心作直线的垂线,证明圆心到直线的距离等于半径,即“作垂直,证半径”.注意:在证明垂直时,常用到直径所对的圆周角是直角这一性质.
有共点、作半径、证垂直
13.如图,△ABC中,∠ACB= 90°,D是边AB上的一点,且∠A=2∠DCB.E是BC上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.
(第13题图)
14.如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.
(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若直线l与AB的延长线相交于点E,⊙O的半径为3,并且∠CAB=30°,求CE的长.
(第14题图)
15.如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线的一点,AE⊥CD交DC的延长线于E,CF⊥AB于F,且CE=CF.
(1)求证:DE是⊙O的切线;
(2)若AB=6,BD=3,求AE和BC的长.
(第15题图)
16.如图所示,在Rt△ABC中,∠C=90°,BC=3,CA=4,∠ABC的角平分线BD交AC于点D,点E是线段AB上的一点,以BE为直径的⊙O过点D.
(1)求证:AC是圆O的切线;
(2)求AE的长.
(第16题图)
17.如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连结AD交BC于F,若AC=FC.
(1)求证:AC是⊙O的切线;
(2)若BF=8,DF=,求⊙O的半径r.
(第17题图)
无共点、作垂直、证半径
18.已知:如图,同心圆O,大圆的弦AB=CD,且AB是小圆的切线,切点为E.求证:CD是小圆的切线.
(第18题图)
19.如图,已知四边形ABCD,∠B=90°,AD∥BC,并且AD+BC=CD,O为AB的中点.
(1)求证:以AB为直径的⊙O与斜腰CD相切;
(2)若OC=8 cm,OD=6 cm,求CD的长.
(第19题图)
答案
与切线有关的长度计算
1.如图,已知⊙O过正方形ABCD的顶点A,B,且与CD边相切,若正方形的边长为2,则圆的半径为( B )
A. B. C. D.1
(第1 题图) 第1题答图
【解析】 如答图,过点O作OE⊥AB于E,连结OA,设⊙O的半径为r,
∵正方形的边长为2,∴AE=1,OE=2-r,
在Rt△OAE中,AE2+OE2=OA2,
即12+(2-r)2=r2,解得r=.
2.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( B )
(第2题图)
A. B. C.3 D.2
解:∵PQ切⊙O于点Q,∴∠Q=90°,
∴PQ2=OP2-OQ2,即PQ=,
当OP最小时,PQ最小,
∵点O到直线l的距离为3,
∴OP的最小值为3,
∴PQ的最小值为=.
3.一个边长为4的等边三角形ABC的高与⊙O的直径相等,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长是( D )
A.2 B. C.2 D.3
(第3题图) 第3题答图
【解析】 如答图,连结OC,并过点O作OF⊥CE于F,
∵△ABC为等边三角形,边长为4,
∴△ABC的高为2,∴OC=,
又∵∠ACB=60°,∴∠OCF=30°,
在Rt△OFC中,可得FC=,∴CE=2FC=3.
4.如图,AB为⊙O的直径,PQ切⊙O于T,AC⊥PQ于C,交⊙O于D.
(1)求证:AT平分∠BAC;
(2)若AD=2,TC=,求⊙O的半径.
(第4题图) 第4题答图
解:(1)证明:如答图,连结OT,
∵PQ切⊙O于T,∴OT⊥PQ,
又∵AC⊥PQ,∴OT∥AC,
∴∠TAC=∠ATO,
又∵OT=OA,∴∠ATO=∠OAT,
∴∠OAT=∠TAC,即AT平分∠BAC.
(2)过点O作OM⊥AC于M,
∴AM=MD==1,
又∵∠OTC=∠ACT=∠OMC=90°,
∴四边形OTCM为矩形,
∴OM=TC=,在Rt△AOM中,
AO===2.
即⊙O的半径为2.
5.如图,在Rt△ABC中,∠B=90°,E为AB上一点,O是BC上一点,∠C=∠BEO,以O为圆心,OB长为半径作⊙O,AC是⊙O的切线.
(1)求证:OE=OC;
(2)若BE=4,BC=8,求OE的长.
(第5题图) 第5题答图
解:(1)证明:设AC切⊙O于Q,连结OQ,如答图,
∵AC是⊙O的切线,∴∠CQO=90°,
在△OQC和△OBE中,
∵∠B=∠CQO=90°,∠C=∠BEO,BO=OQ,
∴△OQC≌△OBE,∴OC=OE;
(2)设OE=OC=x,则BO=8-x,
在Rt△OQC中,OQ2+QC2=OC2,
∴42+(8-x)2=x2,
∴x=5,即OE=5.
6.△ABC内接于⊙O,BC是⊙O的直径.
(1)过点B的切线与OA的延长线交于点P,如图1,若∠C=∠ABC,AB=2,求切线BP的长;
(2)过点A作AD⊥BC于D,交⊙O于H,过点B作弦BF交AD于E,交⊙O于F,且AE=BE,如图2.求证:=.
(第6题图)
解:(1)∵BC是直径,∴∠BAC=90°.
∵∠C=∠ABC,∴∠ABC=∠AOB.
又∵OA=OB,∴△AOB是等边三角形,
∴BO=AB=2,∠AOB=60°,
∵BP是⊙O的切线,∴∠PBO=90°.
在Rt△PBO中,PB=BO=2;
(2)证明:∵AD⊥BC,BC是直径,∴=.
∵AE=BE,∴∠ABF=∠BAH,
∴=,∴=.
与切线有关的角度计算
7.如图,在等腰直角三角形ABC中,AB=AC=4,点O为BC的中点,以O为圆心作⊙O交BC于点M,N,⊙O与AB,AC相切,切点分别为D,E,则⊙O的半径和∠MND的度数分别为( A )
A.2,22.5° B.3,30° C.3,22.5° D.2,30°
(第7题图) 第7题答图
【解析】 如答图,连结OA,
∵AB与⊙O相切,∴OD⊥AB,
∵∠A=90°,∴OD∥AC,
∵O为BC的中点,∴OD=AC=2,
∵∠DOB=45°,
∴∠MND=∠DOB=22.5°.
8.如图,已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D,则∠CDP等于( C )
A.30° B.60° C.45° D.50°
(第8题图) 第8题答图
【解析】 如答图,连结OC,
∵OC=OA,PD平分∠APC,
∴∠CPD=∠DPA,∠A=∠ACO,
∵PC为⊙O的切线,∴OC⊥PC,
∵∠CPO+∠COP=90°,
∴(∠CPD+∠DPA)+(∠A+∠ACO)=90°,
∴∠DPA+∠A=45°,即∠CDP=45°.
9.如图,已知,PD为⊙O的直径,直线BC切⊙O于点C,BP的延长线与CD的延长线交于点A,∠A=28°,∠B=26°,则∠PDC等于( B )
A.34° B.36° C.38° D.40°
(第9题图) 第9题答图
【解析】 如答图,连结OC,
∵直线BC切⊙O于点C,
∴∠OCB=90°,
∵∠A=28°,∠B=26°,
∴∠ACB=180°-∠B-∠A=126°,
∠OCD=∠ACB-∠OCB=36°,
∵OC=OD,∴∠PDC=∠OCD=36°.
10.如图,四边形ABCD内接于⊙O,AB为直径,PD切⊙O于D,与BA延长线交于P点,已知∠C=130°,则∠ADP=__40°__.
(第10题图) 第10题答图
【解析】 如答图,连结OD,
∵四边形ABCD内接于⊙O,∠C=130°,
∴∠DAO=180-∠C=50°,
∵OA=OD,∴∠ODA=∠OAD=50°,
∵PD是⊙O的切线,∴OD⊥PD,
∴∠ADP=90°-∠ODA=40°.
11.如图,已知⊙O上有A,B,C三点,D是OB延长线上的点,∠BDC=30°,CD是⊙O的切线,⊙O的半径为.
(1)求∠A的度数;
(2)如果AC∥BD,请判断四边形ACDB是什么四边形,并求其周长.
( 第11题图) 第11题答图
解:(1)如答图,连结OC,
∵CD是⊙O的切线,∴OC⊥CD,
即∠OCD=90°,
∵∠BDC=30°,∴∠BOC=60°,
∴∠A=∠BOC=30°;
(2)四边形ACDB是平行四边形.
∵AC∥BD,∴∠D+∠ACD=180°,
∴∠ACD=180°-30°=150°,
∴∠ACD+∠BAC=180°,∴AB∥CD,
∴四边形ACDB是平行四边形.
在Rt△DOC中,∠OCD=90°,∠BDC=30°,
∴OD=2OC=2,
∴CD==,BD=OB=,
∴四边形ACDB的周长为:2(+)=2+2.
12.已知⊙O中,AC为直径,MA,MB分别切⊙O于点A,B.
(1)如图1,若∠BAC=25°,求∠M的大小;
(2)如图2,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,求∠M的大小.
(第12题图)
解:(1)∵MA切⊙O于点A,
∴∠MAC=90°.又∵∠BAC=25°,
∴∠MAB=∠MAC-∠BAC=65°.
∵MA,MB分别切⊙O于点A,B,
∴MA=MB,∴∠MAB=∠MBA.
∴∠AMB=180°-(∠MAB+∠MBA)=50°;
(2)如答图,连结AD,AB.
第12题答图
∵MA⊥AC,BD⊥AC,∴BD∥MA.又∵BD=MA.
∴四边形MADB是平行四边形.
∵MA=MB,
∴四边形MADB是菱形,
∴AD=BD.
又∵AC为直径,BD⊥AC,得=,∴AB=AD.
∴△ABD是等边三角形,∴∠D=60°.
∴在菱形MADB中,∠M=∠D=60°.
二、切线的判定
有共点、作半径、证垂直
13.如图,△ABC中,∠ACB= 90°,D是边AB上的一点,且∠A=2∠DCB.E是BC上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.
(第13题图) 第13题答图
解:(1)证明:如答图,连结OD,
∵∠DOB=2∠DCB,又∵∠A=2∠DCB,
∴∠A=∠DOB.又∵∠A+∠B=90°,
∴∠DOB+∠B=90°,∴∠BDO=90°,
∴OD⊥AB,∴AB是⊙O的切线;
(2)如答图,过点O作OM⊥CD于点M,
∵OD=OE=BE=BO,∠BDO=90°,
∴∠B=30°,∴∠DOB=60°,
∴∠DCB=30°,∴OC=2OM=2,
∴OD=2,BO=4,∴BD=2.
14.如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.
(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若直线l与AB的延长线相交于点E,⊙O的半径为3,并且∠CAB=30°,求CE的长.
(第14题图) 第14题答图
解:(1)直线CD与⊙O相切.
理由:如答图,连结OC.
∵OA=OC,∴∠BAC=∠OCA,
∵∠BAC=∠CAM,
∴∠OCA=∠CAM,∴OC∥AM,
∵CD⊥AM,∴OC⊥CD,
∴直线CD与⊙O相切;
(2)∵∠CAB=30°,
∴∠COE=2∠CAB=60°,
∴在Rt△COE中,OC=3,CE=3.
15.如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线的一点,AE⊥CD交DC的延长线于E,CF⊥AB于F,且CE=CF.
(1)求证:DE是⊙O的切线;
(2)若AB=6,BD=3,求AE和BC的长.
(第15题图) 第15题答图
解:(1)证明:如答图,连结OC,
∵AE⊥CD,CF⊥AB,
又∵CE=CF,∴∠1=∠2.
∵OA=OC,∴∠2=∠3,∠1=∠3.
∴OC∥AE.∴OC⊥CD.
∴DE是⊙O的切线;
(2)∵AB=6,∴OB=OC=AB=3.
在Rt△OCD中,OD=OB+BD=6,
OC=3,∴∠D=30°,∠COD=60°.
在Rt△ADE中,AD=AB+BD=9,
∴AE=AD=.
在△OBC中,∵∠COD=60°,OB=OC,
∴BC=OB=3.
16.如图所示,在Rt△ABC中,∠C=90°,BC=3,CA=4,∠ABC的角平分线BD交AC于点D,点E是线段AB上的一点,以BE为直径的⊙O过点D.
(1)求证:AC是圆O的切线;
(2)求AE的长.
(第16题图) 第16题答图
解:(1)证明:如答图,连结OD,
∵OD=OB,∴∠ODB=∠OBD,
∵BD平分∠ABC,
∴∠OBD=∠CBD,即∠ODB=∠CBD,
∴OD∥BC,
∵BC⊥AC,∴OD⊥AC,
又∵点D在⊙O上,∴AC是⊙O的切线;
(2)Rt△ABC中,AC=4,BC=3,则AB=5,
在Rt△AOD中,设AD=4x,则OD=3x,OA=5x,
∵OE=OD=3x,∴AE=OA-OE=2x,
∵AB=AE+BE=2x+6x=5,故x=,
∴AE=2x=.
17.如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连结AD交BC于F,若AC=FC.
(1)求证:AC是⊙O的切线;
(2)若BF=8,DF=,求⊙O的半径r.
(第17题图) 第17题答图
解:(1)如答图,连结OA,OD,
则OA=OD,∴∠OAD=∠ODA,
∵D为BE的下半圆弧的中点,
∴OD⊥BE,∴∠ODA+∠OFD=90°,
∴∠OAD+∠OFD=90°,
∵∠OFD=∠AFC,∴∠OAD+∠AFC=90°,
∵AC=FC,∴∠FAC=∠AFC,
∴∠OAD+∠FAC=90°,∴AC是⊙O的切线;
(2)BF=8,DF=,
∴OF=8-r,∴在Rt△OFD中,
r2+(8-r)2=40,解得r=2.
无共点、作垂直、证半径
18.已知:如图,同心圆O,大圆的弦AB=CD,且AB是小圆的切线,切点为E.求证:CD是小圆的切线.
(第18题图) 第18题答图
证明:如答图所示,连结OE,过O作OF⊥CD于F.
∵AB与小⊙O切于点E,∴OE⊥AB,
∵AB=CD,∴OE=OF,∴CD与小⊙O相切.
19.如图,已知四边形ABCD,∠B=90°,AD∥BC,并且AD+BC=CD,O为AB的中点.
(1)求证:以AB为直径的⊙O与斜腰CD相切;
(2)若OC=8 cm,OD=6 cm,求CD的长.
(第19题图) 第19题答图
解:(1)证明:过点O作OE⊥CD于E.
S梯形ABCD=(AD+BC)·AB
=(AD+BC)·OA
=2
=2(S△OAD+S△OBC),
由S梯形ABCD=S△OBC+ S△OAD+ S△OCD,
∴S△OBC+ S△OAD=S△OCD,
∴AD·OA+BC·OA=CD·OE,
∴(AD+BC)·OA=CD·OE,
又∵AD+BC=CD,∴OA=OE,
∴E点在以AB为直径的⊙O上,
又∵OE⊥CD,∴CD是⊙O的切线;
(2)∵DA,DE均为⊙O的切线,
∴DA=DE,则∠1=∠2,同理∠3=∠4.
∴∠COD=90°.
∴CD===10(cm).
一、切线的性质
(教材P44作业题第5题)
如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于F点,已知AC=12,BC=9,求AO的长.
(教材母题图) 教材母题答图
解:连结OE,如答图所示:
∵BC⊥AC于点C,∴∠C=90°,
在Rt△ABC中,AC=12,BC=9,根据勾股定理得AB=15,
∵AC切半圆于点E,∴OE⊥AC,
∴OE∥BC,∴=,
设OE为x,则AO为15-x,
∴=,解得x=,
则AO=AB-BO=15-=.
与切线有关的长度计算
1.如图,已知⊙O过正方形ABCD的顶点A,B,且与CD边相切,若正方形的边长为2,则圆的半径为( )
A. B. C. D.1
(第1 题图)
2.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
(第2题图)
A. B. C.3 D.2
3.一个边长为4的等边三角形ABC的高与⊙O的直径相等,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长是( )
A.2 B. C.2 D.3
(第3题图)
4.如图,AB为⊙O的直径,PQ切⊙O于T,AC⊥PQ于C,交⊙O于D.
(1)求证:AT平分∠BAC;
(2)若AD=2,TC=,求⊙O的半径.
(第4题图)
5.如图,在Rt△ABC中,∠B=90°,E为AB上一点,O是BC上一点,∠C=∠BEO,以O为圆心,OB长为半径作⊙O,AC是⊙O的切线.
(1)求证:OE=OC;
(2)若BE=4,BC=8,求OE的长.
(第5题图)
6.△ABC内接于⊙O,BC是⊙O的直径.
(1)过点B的切线与OA的延长线交于点P,如图1,若∠C=∠ABC,AB=2,求切线BP的长;
(2)过点A作AD⊥BC于D,交⊙O于H,过点B作弦BF交AD于E,交⊙O于F,且AE=BE,如图2.求证:=.
(第6题图)
与切线有关的角度计算
7.如图,在等腰直角三角形ABC中,AB=AC=4,点O为BC的中点,以O为圆心作⊙O交BC于点M,N,⊙O与AB,AC相切,切点分别为D,E,则⊙O的半径和∠MND的度数分别为( )
A.2,22.5° B.3,30° C.3,22.5° D.2,30°
(第7题图)
8.如图,已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D,则∠CDP等于( )
A.30° B.60° C.45° D.50°
(第8题图)
9.如图,已知,PD为⊙O的直径,直线BC切⊙O于点C,BP的延长线与CD的延长线交于点A,∠A=28°,∠B=26°,则∠PDC等于( )
A.34° B.36° C.38° D.40°
(第9题图)
10.如图,四边形ABCD内接于⊙O,AB为直径,PD切⊙O于D,与BA延长线交于P点,已知∠C=130°,则∠ADP=____.
(第10题图)
11.如图,已知⊙O上有A,B,C三点,D是OB延长线上的点,∠BDC=30°,CD是⊙O的切线,⊙O的半径为.
(1)求∠A的度数;
(2)如果AC∥BD,请判断四边形ACDB是什么四边形,并求其周长.
( 第11题图)
12.已知⊙O中,AC为直径,MA,MB分别切⊙O于点A,B.
(1)如图1,若∠BAC=25°,求∠M的大小;
(2)如图2,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,求∠M的大小.
(第12题图)
二、切线的判定
(教材P44练习题第4题)
已知,如图,PA是⊙O的切线,A是切点,B为⊙O上的一点,PA=PB.求证:PB是⊙O切线.
(教材母题图) 教材母题答图
证明:连结OA,OB,OP,如答图,
在△AOP和△BOP中,
∴△AOP≌△BOP,∵OA⊥AP,
∴OB⊥BP,即PB是⊙O的切线.
【思想方法】证明某直线为圆的切线时,如果该直线与已知圆有公共点,即可作出经过该点的半径,证明直线垂直于该半径,即“连半径,证垂直”;如果不能确定该直线与已知圆有公共点,则过圆心作直线的垂线,证明圆心到直线的距离等于半径,即“作垂直,证半径”.注意:在证明垂直时,常用到直径所对的圆周角是直角这一性质.
有共点、作半径、证垂直
13.如图,△ABC中,∠ACB= 90°,D是边AB上的一点,且∠A=2∠DCB.E是BC上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.
(第13题图)
14.如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.
(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若直线l与AB的延长线相交于点E,⊙O的半径为3,并且∠CAB=30°,求CE的长.
(第14题图)
15.如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线的一点,AE⊥CD交DC的延长线于E,CF⊥AB于F,且CE=CF.
(1)求证:DE是⊙O的切线;
(2)若AB=6,BD=3,求AE和BC的长.
(第15题图)
16.如图所示,在Rt△ABC中,∠C=90°,BC=3,CA=4,∠ABC的角平分线BD交AC于点D,点E是线段AB上的一点,以BE为直径的⊙O过点D.
(1)求证:AC是圆O的切线;
(2)求AE的长.
(第16题图)
17.如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连结AD交BC于F,若AC=FC.
(1)求证:AC是⊙O的切线;
(2)若BF=8,DF=,求⊙O的半径r.
(第17题图)
无共点、作垂直、证半径
18.已知:如图,同心圆O,大圆的弦AB=CD,且AB是小圆的切线,切点为E.求证:CD是小圆的切线.
(第18题图)
19.如图,已知四边形ABCD,∠B=90°,AD∥BC,并且AD+BC=CD,O为AB的中点.
(1)求证:以AB为直径的⊙O与斜腰CD相切;
(2)若OC=8 cm,OD=6 cm,求CD的长.
(第19题图)
答案
与切线有关的长度计算
1.如图,已知⊙O过正方形ABCD的顶点A,B,且与CD边相切,若正方形的边长为2,则圆的半径为( B )
A. B. C. D.1
(第1 题图) 第1题答图
【解析】 如答图,过点O作OE⊥AB于E,连结OA,设⊙O的半径为r,
∵正方形的边长为2,∴AE=1,OE=2-r,
在Rt△OAE中,AE2+OE2=OA2,
即12+(2-r)2=r2,解得r=.
2.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( B )
(第2题图)
A. B. C.3 D.2
解:∵PQ切⊙O于点Q,∴∠Q=90°,
∴PQ2=OP2-OQ2,即PQ=,
当OP最小时,PQ最小,
∵点O到直线l的距离为3,
∴OP的最小值为3,
∴PQ的最小值为=.
3.一个边长为4的等边三角形ABC的高与⊙O的直径相等,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长是( D )
A.2 B. C.2 D.3
(第3题图) 第3题答图
【解析】 如答图,连结OC,并过点O作OF⊥CE于F,
∵△ABC为等边三角形,边长为4,
∴△ABC的高为2,∴OC=,
又∵∠ACB=60°,∴∠OCF=30°,
在Rt△OFC中,可得FC=,∴CE=2FC=3.
4.如图,AB为⊙O的直径,PQ切⊙O于T,AC⊥PQ于C,交⊙O于D.
(1)求证:AT平分∠BAC;
(2)若AD=2,TC=,求⊙O的半径.
(第4题图) 第4题答图
解:(1)证明:如答图,连结OT,
∵PQ切⊙O于T,∴OT⊥PQ,
又∵AC⊥PQ,∴OT∥AC,
∴∠TAC=∠ATO,
又∵OT=OA,∴∠ATO=∠OAT,
∴∠OAT=∠TAC,即AT平分∠BAC.
(2)过点O作OM⊥AC于M,
∴AM=MD==1,
又∵∠OTC=∠ACT=∠OMC=90°,
∴四边形OTCM为矩形,
∴OM=TC=,在Rt△AOM中,
AO===2.
即⊙O的半径为2.
5.如图,在Rt△ABC中,∠B=90°,E为AB上一点,O是BC上一点,∠C=∠BEO,以O为圆心,OB长为半径作⊙O,AC是⊙O的切线.
(1)求证:OE=OC;
(2)若BE=4,BC=8,求OE的长.
(第5题图) 第5题答图
解:(1)证明:设AC切⊙O于Q,连结OQ,如答图,
∵AC是⊙O的切线,∴∠CQO=90°,
在△OQC和△OBE中,
∵∠B=∠CQO=90°,∠C=∠BEO,BO=OQ,
∴△OQC≌△OBE,∴OC=OE;
(2)设OE=OC=x,则BO=8-x,
在Rt△OQC中,OQ2+QC2=OC2,
∴42+(8-x)2=x2,
∴x=5,即OE=5.
6.△ABC内接于⊙O,BC是⊙O的直径.
(1)过点B的切线与OA的延长线交于点P,如图1,若∠C=∠ABC,AB=2,求切线BP的长;
(2)过点A作AD⊥BC于D,交⊙O于H,过点B作弦BF交AD于E,交⊙O于F,且AE=BE,如图2.求证:=.
(第6题图)
解:(1)∵BC是直径,∴∠BAC=90°.
∵∠C=∠ABC,∴∠ABC=∠AOB.
又∵OA=OB,∴△AOB是等边三角形,
∴BO=AB=2,∠AOB=60°,
∵BP是⊙O的切线,∴∠PBO=90°.
在Rt△PBO中,PB=BO=2;
(2)证明:∵AD⊥BC,BC是直径,∴=.
∵AE=BE,∴∠ABF=∠BAH,
∴=,∴=.
与切线有关的角度计算
7.如图,在等腰直角三角形ABC中,AB=AC=4,点O为BC的中点,以O为圆心作⊙O交BC于点M,N,⊙O与AB,AC相切,切点分别为D,E,则⊙O的半径和∠MND的度数分别为( A )
A.2,22.5° B.3,30° C.3,22.5° D.2,30°
(第7题图) 第7题答图
【解析】 如答图,连结OA,
∵AB与⊙O相切,∴OD⊥AB,
∵∠A=90°,∴OD∥AC,
∵O为BC的中点,∴OD=AC=2,
∵∠DOB=45°,
∴∠MND=∠DOB=22.5°.
8.如图,已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D,则∠CDP等于( C )
A.30° B.60° C.45° D.50°
(第8题图) 第8题答图
【解析】 如答图,连结OC,
∵OC=OA,PD平分∠APC,
∴∠CPD=∠DPA,∠A=∠ACO,
∵PC为⊙O的切线,∴OC⊥PC,
∵∠CPO+∠COP=90°,
∴(∠CPD+∠DPA)+(∠A+∠ACO)=90°,
∴∠DPA+∠A=45°,即∠CDP=45°.
9.如图,已知,PD为⊙O的直径,直线BC切⊙O于点C,BP的延长线与CD的延长线交于点A,∠A=28°,∠B=26°,则∠PDC等于( B )
A.34° B.36° C.38° D.40°
(第9题图) 第9题答图
【解析】 如答图,连结OC,
∵直线BC切⊙O于点C,
∴∠OCB=90°,
∵∠A=28°,∠B=26°,
∴∠ACB=180°-∠B-∠A=126°,
∠OCD=∠ACB-∠OCB=36°,
∵OC=OD,∴∠PDC=∠OCD=36°.
10.如图,四边形ABCD内接于⊙O,AB为直径,PD切⊙O于D,与BA延长线交于P点,已知∠C=130°,则∠ADP=__40°__.
(第10题图) 第10题答图
【解析】 如答图,连结OD,
∵四边形ABCD内接于⊙O,∠C=130°,
∴∠DAO=180-∠C=50°,
∵OA=OD,∴∠ODA=∠OAD=50°,
∵PD是⊙O的切线,∴OD⊥PD,
∴∠ADP=90°-∠ODA=40°.
11.如图,已知⊙O上有A,B,C三点,D是OB延长线上的点,∠BDC=30°,CD是⊙O的切线,⊙O的半径为.
(1)求∠A的度数;
(2)如果AC∥BD,请判断四边形ACDB是什么四边形,并求其周长.
( 第11题图) 第11题答图
解:(1)如答图,连结OC,
∵CD是⊙O的切线,∴OC⊥CD,
即∠OCD=90°,
∵∠BDC=30°,∴∠BOC=60°,
∴∠A=∠BOC=30°;
(2)四边形ACDB是平行四边形.
∵AC∥BD,∴∠D+∠ACD=180°,
∴∠ACD=180°-30°=150°,
∴∠ACD+∠BAC=180°,∴AB∥CD,
∴四边形ACDB是平行四边形.
在Rt△DOC中,∠OCD=90°,∠BDC=30°,
∴OD=2OC=2,
∴CD==,BD=OB=,
∴四边形ACDB的周长为:2(+)=2+2.
12.已知⊙O中,AC为直径,MA,MB分别切⊙O于点A,B.
(1)如图1,若∠BAC=25°,求∠M的大小;
(2)如图2,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,求∠M的大小.
(第12题图)
解:(1)∵MA切⊙O于点A,
∴∠MAC=90°.又∵∠BAC=25°,
∴∠MAB=∠MAC-∠BAC=65°.
∵MA,MB分别切⊙O于点A,B,
∴MA=MB,∴∠MAB=∠MBA.
∴∠AMB=180°-(∠MAB+∠MBA)=50°;
(2)如答图,连结AD,AB.
第12题答图
∵MA⊥AC,BD⊥AC,∴BD∥MA.又∵BD=MA.
∴四边形MADB是平行四边形.
∵MA=MB,
∴四边形MADB是菱形,
∴AD=BD.
又∵AC为直径,BD⊥AC,得=,∴AB=AD.
∴△ABD是等边三角形,∴∠D=60°.
∴在菱形MADB中,∠M=∠D=60°.
二、切线的判定
有共点、作半径、证垂直
13.如图,△ABC中,∠ACB= 90°,D是边AB上的一点,且∠A=2∠DCB.E是BC上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.
(第13题图) 第13题答图
解:(1)证明:如答图,连结OD,
∵∠DOB=2∠DCB,又∵∠A=2∠DCB,
∴∠A=∠DOB.又∵∠A+∠B=90°,
∴∠DOB+∠B=90°,∴∠BDO=90°,
∴OD⊥AB,∴AB是⊙O的切线;
(2)如答图,过点O作OM⊥CD于点M,
∵OD=OE=BE=BO,∠BDO=90°,
∴∠B=30°,∴∠DOB=60°,
∴∠DCB=30°,∴OC=2OM=2,
∴OD=2,BO=4,∴BD=2.
14.如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.
(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若直线l与AB的延长线相交于点E,⊙O的半径为3,并且∠CAB=30°,求CE的长.
(第14题图) 第14题答图
解:(1)直线CD与⊙O相切.
理由:如答图,连结OC.
∵OA=OC,∴∠BAC=∠OCA,
∵∠BAC=∠CAM,
∴∠OCA=∠CAM,∴OC∥AM,
∵CD⊥AM,∴OC⊥CD,
∴直线CD与⊙O相切;
(2)∵∠CAB=30°,
∴∠COE=2∠CAB=60°,
∴在Rt△COE中,OC=3,CE=3.
15.如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线的一点,AE⊥CD交DC的延长线于E,CF⊥AB于F,且CE=CF.
(1)求证:DE是⊙O的切线;
(2)若AB=6,BD=3,求AE和BC的长.
(第15题图) 第15题答图
解:(1)证明:如答图,连结OC,
∵AE⊥CD,CF⊥AB,
又∵CE=CF,∴∠1=∠2.
∵OA=OC,∴∠2=∠3,∠1=∠3.
∴OC∥AE.∴OC⊥CD.
∴DE是⊙O的切线;
(2)∵AB=6,∴OB=OC=AB=3.
在Rt△OCD中,OD=OB+BD=6,
OC=3,∴∠D=30°,∠COD=60°.
在Rt△ADE中,AD=AB+BD=9,
∴AE=AD=.
在△OBC中,∵∠COD=60°,OB=OC,
∴BC=OB=3.
16.如图所示,在Rt△ABC中,∠C=90°,BC=3,CA=4,∠ABC的角平分线BD交AC于点D,点E是线段AB上的一点,以BE为直径的⊙O过点D.
(1)求证:AC是圆O的切线;
(2)求AE的长.
(第16题图) 第16题答图
解:(1)证明:如答图,连结OD,
∵OD=OB,∴∠ODB=∠OBD,
∵BD平分∠ABC,
∴∠OBD=∠CBD,即∠ODB=∠CBD,
∴OD∥BC,
∵BC⊥AC,∴OD⊥AC,
又∵点D在⊙O上,∴AC是⊙O的切线;
(2)Rt△ABC中,AC=4,BC=3,则AB=5,
在Rt△AOD中,设AD=4x,则OD=3x,OA=5x,
∵OE=OD=3x,∴AE=OA-OE=2x,
∵AB=AE+BE=2x+6x=5,故x=,
∴AE=2x=.
17.如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连结AD交BC于F,若AC=FC.
(1)求证:AC是⊙O的切线;
(2)若BF=8,DF=,求⊙O的半径r.
(第17题图) 第17题答图
解:(1)如答图,连结OA,OD,
则OA=OD,∴∠OAD=∠ODA,
∵D为BE的下半圆弧的中点,
∴OD⊥BE,∴∠ODA+∠OFD=90°,
∴∠OAD+∠OFD=90°,
∵∠OFD=∠AFC,∴∠OAD+∠AFC=90°,
∵AC=FC,∴∠FAC=∠AFC,
∴∠OAD+∠FAC=90°,∴AC是⊙O的切线;
(2)BF=8,DF=,
∴OF=8-r,∴在Rt△OFD中,
r2+(8-r)2=40,解得r=2.
无共点、作垂直、证半径
18.已知:如图,同心圆O,大圆的弦AB=CD,且AB是小圆的切线,切点为E.求证:CD是小圆的切线.
(第18题图) 第18题答图
证明:如答图所示,连结OE,过O作OF⊥CD于F.
∵AB与小⊙O切于点E,∴OE⊥AB,
∵AB=CD,∴OE=OF,∴CD与小⊙O相切.
19.如图,已知四边形ABCD,∠B=90°,AD∥BC,并且AD+BC=CD,O为AB的中点.
(1)求证:以AB为直径的⊙O与斜腰CD相切;
(2)若OC=8 cm,OD=6 cm,求CD的长.
(第19题图) 第19题答图
解:(1)证明:过点O作OE⊥CD于E.
S梯形ABCD=(AD+BC)·AB
=(AD+BC)·OA
=2
=2(S△OAD+S△OBC),
由S梯形ABCD=S△OBC+ S△OAD+ S△OCD,
∴S△OBC+ S△OAD=S△OCD,
∴AD·OA+BC·OA=CD·OE,
∴(AD+BC)·OA=CD·OE,
又∵AD+BC=CD,∴OA=OE,
∴E点在以AB为直径的⊙O上,
又∵OE⊥CD,∴CD是⊙O的切线;
(2)∵DA,DE均为⊙O的切线,
∴DA=DE,则∠1=∠2,同理∠3=∠4.
∴∠COD=90°.
∴CD===10(cm).
