浙教版九年级圆的性质的综合运用专题(含答案)
文档属性
| 名称 | 浙教版九年级圆的性质的综合运用专题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 375.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-28 16:38:06 | ||
图片预览


文档简介
圆的性质的综合运用
(教材P93作业题第6题)
如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上任意一点,连结AD,GD.找出图中和∠ADC相等的角,并给出证明.
(教材母题图)
解:∠G=∠ADC,
证明:连结AC,
∵AB是圆O的直径,弦CD⊥AB,
∴AB垂直平分CD,∴=,
∴∠G=∠ADC.
垂径定理、圆心角定理圆周角定理的综合运用
1.[金华校级期中]如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,则CD的长为( )
(第1题图)
A.2 B.4
C.4 D.8
2.[嘉兴校级期中]如图,在Rt△ABC中,∠ACB=90°,AC=3,BC= 4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
A. B. C. D.
(第2题图)
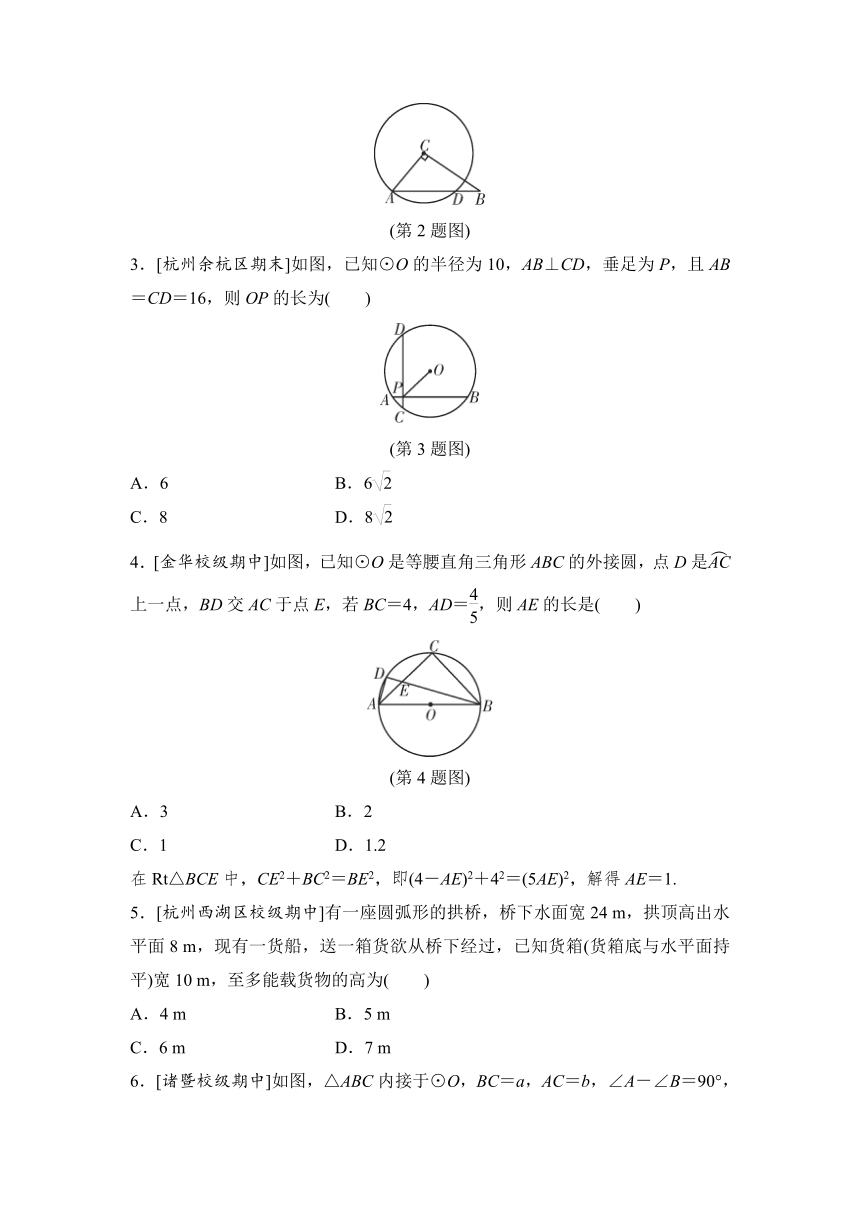
3.[杭州余杭区期末]如图,已知⊙O的半径为10,AB⊥CD,垂足为P,且AB=CD=16,则OP的长为( )
(第3题图)
A.6 B.6
C.8 D.8
4.[金华校级期中]如图,已知⊙O是等腰直角三角形ABC的外接圆,点D是上一点,BD交AC于点E,若BC=4,AD=,则AE的长是( )
(第4题图)
A.3 B.2
C.1 D.1.2
在Rt△BCE中,CE2+BC2=BE2,即(4-AE)2+42=(5AE)2,解得AE=1.
5.[杭州西湖区校级期中]有一座圆弧形的拱桥,桥下水面宽24 m,拱顶高出水平面8 m,现有一货船,送一箱货欲从桥下经过,已知货箱(货箱底与水平面持平)宽10 m,至多能载货物的高为( )
A.4 m B.5 m
C.6 m D.7 m
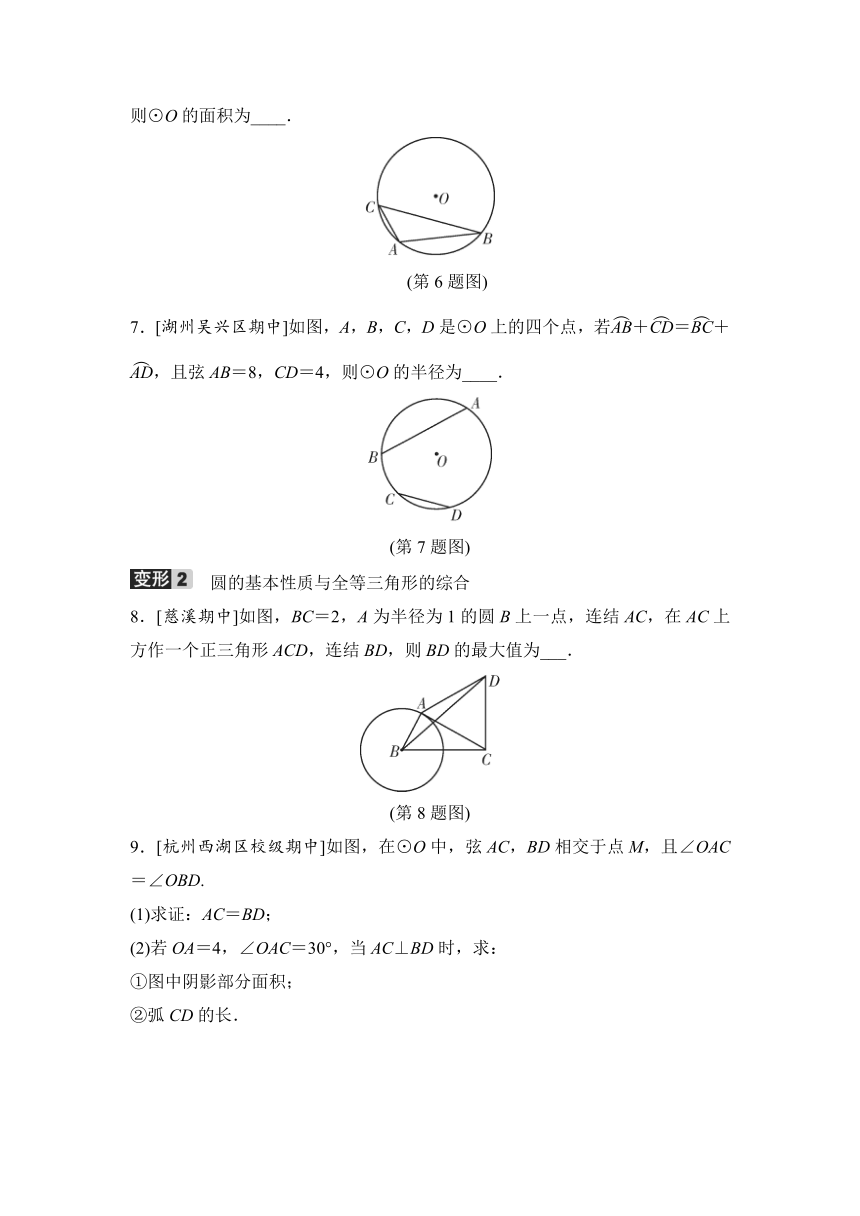
6.[诸暨校级期中]如图,△ABC内接于⊙O,BC=a,AC=b,∠A-∠B=90°,则⊙O的面积为____.
(第6题图)
7.[湖州吴兴区期中]如图,A,B,C,D是⊙O上的四个点,若+=+,且弦AB=8,CD=4,则⊙O的半径为____.
(第7题图)
圆的基本性质与全等三角形的综合
8.[慈溪期中]如图,BC=2,A为半径为1的圆B上一点,连结AC,在AC上方作一个正三角形ACD,连结BD,则BD的最大值为___.
(第8题图)
9.[杭州西湖区校级期中]如图,在⊙O中,弦AC,BD相交于点M,且∠OAC=∠OBD.
(1)求证:AC=BD;
(2)若OA=4,∠OAC=30°,当AC⊥BD时,求:
①图中阴影部分面积;
②弧CD的长.
(第9题图)
10.[杭州江干区期末]如图,⊙O是△ABC的外接圆,AC是直径,过O作OD∥BC交AB于点D.延长DO交⊙O于点E,作EF⊥AC于点F,连结DF并延长交直线BC于点G,连结EG.
(1)求证:FC=GC;
(2)四边形EDBG是哪种特殊四边形?请说明理由.
(第10题图)
圆与内、外角平分线问题
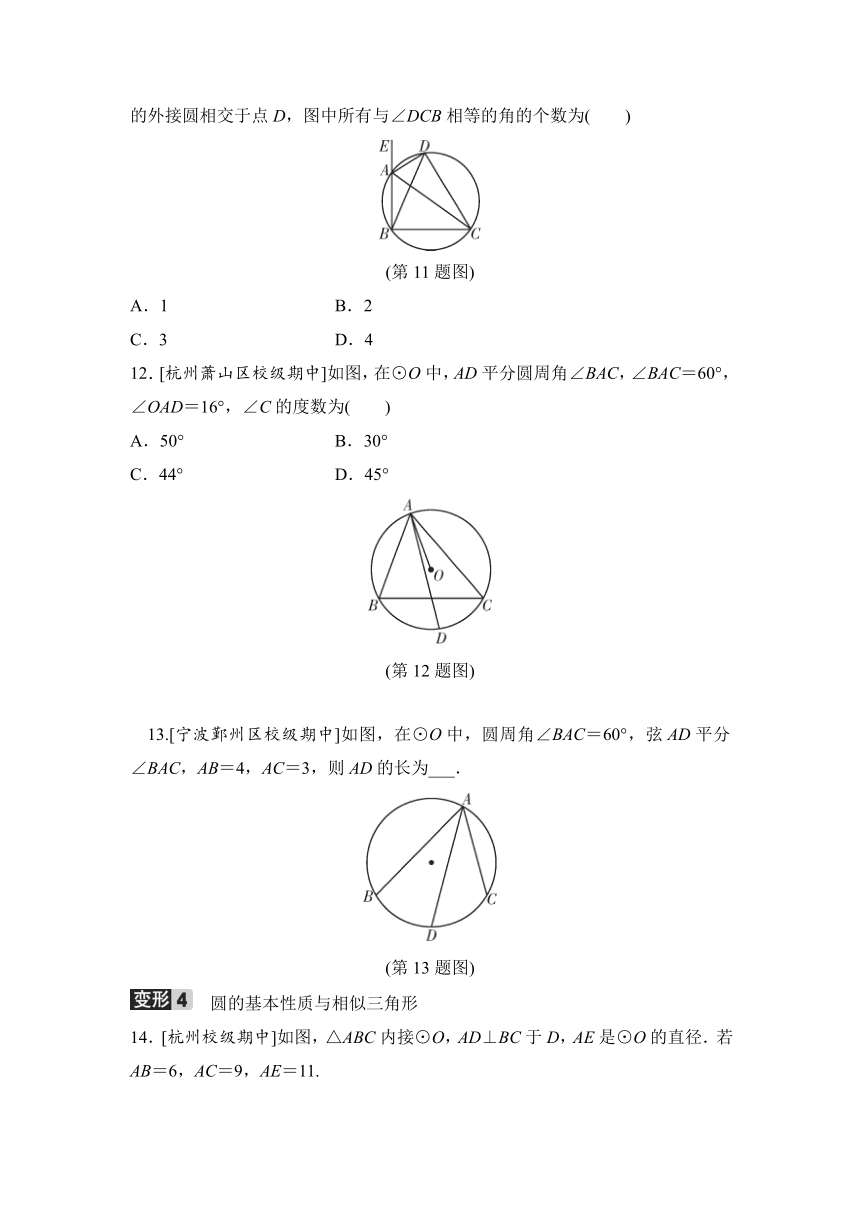
11.[杭州萧山区校级期中]如图,AD是△ABC外角∠EAC的平分线,AD与△ABC的外接圆相交于点D,图中所有与∠DCB相等的角的个数为( )
(第11题图)
A.1 B.2
C.3 D.4
12.[杭州萧山区校级期中]如图,在⊙O中,AD平分圆周角∠BAC,∠BAC=60°,∠OAD=16°,∠C的度数为( )
A.50° B.30°
C.44° D.45°
(第12题图)
13.[宁波鄞州区校级期中]如图,在⊙O中,圆周角∠BAC=60°,弦AD平分∠BAC,AB=4,AC=3,则AD的长为___.
(第13题图)
圆的基本性质与相似三角形
14.[杭州校级期中]如图,△ABC内接⊙O,AD⊥BC于D,AE是⊙O的直径.若AB=6,AC=9,AE=11.
(第14题图)
(1)求证:△ABD∽△AEC;
(2)求AD的长.
15.[衢州校级期中]如图,已知AB为⊙O的直径,弦BE=DE,且AD,BE的延长线交于点C.
(1)求证:AC=AB;
(2)若CE=2,CD=,求⊙O的直径.
(第15题图)
16.[杭州校级期中]如图,AB为⊙O的直径,弦CD⊥AB于点E,点G是上一点,连结AC,AG,CG.
(1)在不添辅助线的前提下直接写出图中与∠AGC相等的角,不用证明;
(2)求证:当AB∥DG时,△ACG与△EAC相似;
(第16题图) 备用图
(3)若OE=BE,求∠AGC的度数.
17.[杭州校级期中]如图,已知A,P,B,C是⊙O上的四点,∠APC=∠BPC=60°,AB与PC交于Q点.
(1)判断△ABC 的形状,并证明你的结论;
(2)直接写出所有与△APQ相似的三角形:__ __;
(3)若AP=6,=,求PB的长.
(第17题图)
圆的综合探究
18.[杭州余杭区期末]已知:如图,AB是圆O的直径,CD是圆O的弦,AB⊥CD,E为垂足,AE=CD=8,F是CD延长线上一点,连结AF交圆O于G,连结AD,DG.
(1)求圆O的半径;
(2)求证:△ADG∽△AFD;
(3)当点G是弧AD的中点时,求△ADG的面积与△AFD的面积之比.
(第18题图)
19.[宁波北仑区期末]如图,在⊙O中,弦AB,CD相交于点E,=,点D在上,连结CO,并延长CO交线段AB于点F,连结OA,OB,且OA=,tan∠OBA=.
(1)求证:∠OBA=∠OCD;
(2)当△AOF是直角三角形时,求EF的长;
(3)是否存在点F,使得S△CEF=4S△BOF,若存在,请求出EF的长;若不存在,请说明理由.
(第19题图) 备用图
答案
垂径定理、圆心角定理圆周角定理的综合运用
1.[金华校级期中]如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,则CD的长为( C )
(第1题图)
A.2 B.4
C.4 D.8
解:∵∠A=22.5°,
∴∠BOC=2∠A=45°,
∵⊙O的直径AB垂直于弦CD,
∴CE=DE,△OCE为等腰直角三角形,
∴CE=OC=2,
∴CD=2CE=4.
2.[嘉兴校级期中]如图,在Rt△ABC中,∠ACB=90°,AC=3,BC= 4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( C )
A. B. C. D.
(第2题图) 第2题答图
解:过C作CM⊥AB,交AB于点M,如答图所示,
∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB==5,
∵CM⊥AB,∴M为AD的中点,
∵S△ABC=AC·BC=AB·CM,且AC=3,BC=4,AB=5,∴CM=,
在Rt△ACM中,AC2=AM2+CM2,即32=AM2+,解得AM=,∴AD=2AM=.
3.[杭州余杭区期末]如图,已知⊙O的半径为10,AB⊥CD,垂足为P,且AB=CD=16,则OP的长为( B )
(第3题图)
A.6 B.6
C.8 D.8
【解析】 作OM⊥AB于M,ON⊥CD于N,连结OB,OD,
∵AB=CD=16,∴BM=DN=8,
∴OM=ON==6,
∵AB⊥CD,OM⊥AB,ON⊥CD,
∴四边形MONP是正方形,
∴OP==6.故选B.
4.[金华校级期中]如图,已知⊙O是等腰直角三角形ABC的外接圆,点D是上一点,BD交AC于点E,若BC=4,AD=,则AE的长是( C )
(第4题图)
A.3 B.2
C.1 D.1.2
解:在等腰直角三角形ABC中,BC=4,
∴AB是⊙O的直径,AC=4,∴∠D=90°,
∵∠D=∠C,∠DAC=∠CBE,
∴△ADE∽△BCE,
∴==,即BE=5AE,
在Rt△BCE中,CE2+BC2=BE2,即(4-AE)2+42=(5AE)2,解得AE=1.
5.[杭州西湖区校级期中]有一座圆弧形的拱桥,桥下水面宽24 m,拱顶高出水平面8 m,现有一货船,送一箱货欲从桥下经过,已知货箱(货箱底与水平面持平)宽10 m,至多能载货物的高为( D )
A.4 m B.5 m
C.6 m D.7 m
解:如答图,表示桥拱,AB=24 m,CD=8 m,EF=10 m,D为AB,EF的中点,且CD,ME,NF均垂直于AB,
第5题答图
设所在圆的圆心为O,连结OA,ON,设OA=R,
则OD=OC-DC=R-8,AD=AB=12 m,
又∵OA2=AD2+OD2,
即R2=122+(R-8)2,解得R=13(m).
在Rt△ONG中,由勾股定理得,OG==12 m,
∴FN=DG=OG-OD=OG-(OC-CD)=7 m.故选D.
6.[诸暨校级期中]如图,△ABC内接于⊙O,BC=a,AC=b,∠A-∠B=90°,则⊙O的面积为__(a2+b2)__.
(第6题图) 第6题答图
【解析】 如答图,过点B作圆的直径BE交圆于点E,则∠ECB=90°,
∴∠E+∠EBC=90°,
又∵圆内接四边形的对角互补,即∠E+∠A=180°,∴∠A-∠EBC=90°,
∵∠A-∠ABC=90°,∴∠CBA=∠CBE,
∴弧AC=弧CE,∴CE=AC=b,
由勾股定理得,BE=,
∴⊙O的半径=,
∴圆的面积=(a2+b2).
7.[湖州吴兴区期中]如图,A,B,C,D是⊙O上的四个点,若+=+,且弦AB=8,CD=4,则⊙O的半径为__2__.
(第7题图) 第7题答图
【解析】 如答图,连结BO并延长,与圆交于E,连结AE,
+=+,所以AB,CD所对圆心角之和是180°,
∴CD=AE,∠A=90°,
BE===4,
∴半径是2.
圆的基本性质与全等三角形的综合
8.[慈溪期中]如图,BC=2,A为半径为1的圆B上一点,连结AC,在AC上方作一个正三角形ACD,连结BD,则BD的最大值为__3__.
(第8题图) 第8题答图
【解析】 如答图,将BC绕点C顺时针旋转60°到点M,连结MD,MB,当点B,M,D共线时,BD有最大值,
∵∠BCM=60°,CM=BC=2,
∴△BCM是等边三角形,∴BM=2,
∵∠BCM=∠ACD=60°,∴∠ACB=∠MCD,
∵AC=CD,BC=CM,
∴△ABC≌△DMC,∴DM=AB=1,
∴BD=3.
9.[杭州西湖区校级期中]如图,在⊙O中,弦AC,BD相交于点M,且∠OAC=∠OBD.
(1)求证:AC=BD;
(2)若OA=4,∠OAC=30°,当AC⊥BD时,求:
①图中阴影部分面积;
②弧CD的长.
(第9题图) 第9题答图
解:(1)连结OC,OD,
∵OA=OC,∴∠CAO=∠ACO,
∵OD=OB,∴∠ODB=∠OBD,
∵ ∠OAC=∠OBD,∴∠CAO=∠ACO=∠ODB=∠OBD,
∵
∴△OAC≌△ODB(AAS),∴AC=BD;
(2)如答图,作ON⊥AC于N,OP⊥BD于P,连结OM,
由(1)可知AC=BD,∴ON=OP,
∵AC⊥BD,OP⊥BD,ON⊥AC,ON=OP,
∴四边形OPMN是正方形,
∴∠AMO=∠BMO=45°,
∵
∴△AMO≌△BMO,∴S△AMO=S△BMO,
∵OA=4,∠OAC=30°,
∴ON=2,AN=2,MN=2,
∵∠MOA=45°+60°=105°,
∴∠AOB=360°-105°×2=150°;
①S阴影=S扇AOB+ 2S△AOM
=×πr2+2××(2+2)×2=+4+4;
②∠DOC=∠AOC+∠DOB+∠AOB-360°=30°,
∴=×2πr=π.
10.[杭州江干区期末]如图,⊙O是△ABC的外接圆,AC是直径,过O作OD∥BC交AB于点D.延长DO交⊙O于点E,作EF⊥AC于点F,连结DF并延长交直线BC于点G,连结EG.
(1)求证:FC=GC;
(2)四边形EDBG是哪种特殊四边形?请说明理由.
(第10题图) 第10题答图
解:(1)证明:∵AC为直径,∴∠B=90°,
∵OD∥BC,∴∠ADO=∠B=90°,
在△AOD和△EOF中,
∴△AOD≌△EOF,∴OD=OF,
∴∠ODF=∠OFD,
∵OD∥BC,∴∠FGC=∠ODF,
又∵∠GFC=∠OFD,∴∠CFG=∠FGC,
∴FC=GC;
(2)四边形EDBG是矩形,理由如下:
如答图,连结AE,EC,
∵OA=OE,∴∠OAE=∠OEA,
∵OD=OF,∴∠ODF=∠OFD,
∴∠OAE=∠OFD,∴AE∥DG,
∵AC为直径,∴∠AEC=90°,
又∵CF=CG,∴CE是FG的垂直平分线,
∴△EFC≌△EGC,
∴∠EGC=∠EFC=90°,
又∵∠EDB=90°,∠ABC=90°,
∴四边形EDBG是矩形.
圆与内、外角平分线问题
11.[杭州萧山区校级期中]如图,AD是△ABC外角∠EAC的平分线,AD与△ABC的外接圆相交于点D,图中所有与∠DCB相等的角的个数为( C )
(第11题图)
A.1 B.2
C.3 D.4
【解析】 ∵A,B,C,D四点共圆,
∴∠DCB=∠EAD,
∵AD是△ABC外角∠EAC的平分线,
∴∠EAD=∠CAD=∠EAC,
∴∠EAD=∠CAD=∠BCD=∠DBC.故选C.
12.[杭州萧山区校级期中]如图,在⊙O中,AD平分圆周角∠BAC,∠BAC=60°,∠OAD=16°,∠C的度数为( C )
A.50° B.30°
C.44° D.45°
(第12题图) 第12题答图
【解析】 如答图,连结OD,CD,
∵OA=OD,∴∠OAD=∠ODA=16°,
∴∠AOD=148°,∴∠ACD=74°,
∵∠BAC=60°,AD平分圆周角∠BAC,
∴∠BAD=30°,∴∠BCD=30°,
∴∠ACB=∠ACD-∠BCD=44°.
13.[宁波鄞州区校级期中]如图,在⊙O中,圆周角∠BAC=60°,弦AD平分∠BAC,AB=4,AC=3,则AD的长为____.
(第13题图) 第13题答图
【解析】 如答图,连结BD,CD,过点B作BN⊥AD于N,过点C作CM⊥AD于M.
∵∠BAC=60°,AD平分∠BAC,
∴∠BAD=∠CAD=30°,
∵AB=4,∠BAD=30°,BN⊥AD,
∴BN=2,AN=2,
∵AC=3,∠CAD=30°,CM⊥AD,
∴CM=,AM=,∴MN=,
设DN=a,
∵∠BAD=∠CAD,∴BD=CD,
由勾股定理得BN2+DN2=CM2+DM2,即22+a2=+,
解得a=,∴AD=AN+DN=.
圆的基本性质与相似三角形
14.[杭州校级期中]如图,△ABC内接⊙O,AD⊥BC于D,AE是⊙O的直径.若AB=6,AC=9,AE=11.
(第14题图)
(1)求证:△ABD∽△AEC;
(2)求AD的长.
解:(1)证明:∵AE是⊙O的直径,AD⊥BC,
∴∠ACE=∠ADB=90°,
∵∠E=∠B,∴△ABD∽△AEC;
(2)∵△ABD ∽△AEC,∴=,
∵AB=6,AC=9,AE=11,∴AD=.
15.[衢州校级期中]如图,已知AB为⊙O的直径,弦BE=DE,且AD,BE的延长线交于点C.
(1)求证:AC=AB;
(2)若CE=2,CD=,求⊙O的直径.
(第15题图) 第15题答图
解:(1)证明:如答图,连结AE,
∵AB为⊙O的直径,
∴∠AEB=90°,∴∠AEB=∠AEC=90°,
∵BE=DE,
∴=,∴∠DAE=∠BAE,
∵∠C=90°-∠DAE,∠B=90°-∠BAE,
∴∠B=∠C,∴AC=AB;
(2)∵∠C=∠C,∠CED=∠CAB,
∴△CDE∽△CBA,∴=,
∴CD·CA=CB·CE,∴×AC=2×4,
∴AC=.∴⊙O的直径为.
16.[杭州校级期中]如图,AB为⊙O的直径,弦CD⊥AB于点E,点G是上一点,连结AC,AG,CG.
(1)在不添辅助线的前提下直接写出图中与∠AGC相等的角,不用证明;
(2)求证:当AB∥DG时,△ACG与△EAC相似;
(第16题图) 备用图
(3)若OE=BE,求∠AGC的度数.
解:(1)结论:∠ACE=∠AGC.
(2)证明:∵DG∥AB,
第16题答图
∴∠AEC=∠CDG=90°,
∴CG是直径,∴∠CAG=90°,
∵∠CAG=∠AEC=90°,∠AGC=∠ACE,
∴△ACG∽△EAC.
(3)如答图,连结OC,BC.
∵OE=EB,CE⊥OB,
∴CO=CB=OB,
∴△OBC是等边三角形,
∴∠B=60°,∴∠AGC=∠B=60°.
17.[杭州校级期中]如图,已知A,P,B,C是⊙O上的四点,∠APC=∠BPC=60°,AB与PC交于Q点.
(1)判断△ABC 的形状,并证明你的结论;
(2)直接写出所有与△APQ相似的三角形:__△CBQ和△CPB__;
(3)若AP=6,=,求PB的长.
(第17题图) 第17题答图
解:(1)△ABC是等边三角形.
∵∠BPC=∠APC=60°,∠BAC=∠ABC=60°,
∴△ABC是等边三角形;
(2)△CBQ和△CPB.
(3)如答图,过B作BD∥PA交PC于D,
则∠BDP=∠APC=60°.
又∵∠AQP=∠BQD,
∴△AQP∽△BQD,∴=,
∵∠BPD=∠BDP=60°,∴PB=BD.
∴=,∴=,∴PB=10.
圆的综合探究
18.[杭州余杭区期末]已知:如图,AB是圆O的直径,CD是圆O的弦,AB⊥CD,E为垂足,AE=CD=8,F是CD延长线上一点,连结AF交圆O于G,连结AD,DG.
(1)求圆O的半径;
(2)求证:△ADG∽△AFD;
(3)当点G是弧AD的中点时,求△ADG的面积与△AFD的面积之比.
(第18题图) 第18题答图
解:(1)如答图,连结OC,设⊙O的半径为R,
∵AE=8,∴OE=8-R,
∵直径AB⊥CD,
∴∠CEO=90°,CE=CD=4,
在Rt△CEO中,根据勾股定理得,R2-(8-R)2=16,∴R=5,
即⊙O的半径为5;
(2)如答图,连结BG,
∴∠ADG=∠ABG,
∵AB是⊙O的直径,∴∠AGB=90°,
∴∠ABG+∠BAG=90°,
∴∠ADG+∠BAG=90°,
∵AB⊥CD,∴∠BAG+∠F=90°,
∴∠ADG=∠F,
∵∠DAG=∠FAD,∴△ADG∽△AFD;
(3)如答图,连结OG交AD于H,
在Rt△ADE中,AE=8,DE=CD=4,根据勾股定理得,AD=4,
∵点G是的中点,
∴AH=AD=2,OG⊥AD,
在Rt△AOH中,根据勾股定理得,OH=,
在Rt△AHG中,HG=OG-OH=5-,根据勾股定理得,AG2=AH2+HG2=50-10,
由(2)知,△ADG∽△AFD,
∴===.
19.[宁波北仑区期末]如图,在⊙O中,弦AB,CD相交于点E,=,点D在上,连结CO,并延长CO交线段AB于点F,连结OA,OB,且OA=,tan∠OBA=.
(1)求证:∠OBA=∠OCD;
(2)当△AOF是直角三角形时,求EF的长;
(3)是否存在点F,使得S△CEF=4S△BOF,若存在,请求出EF的长;若不存在,请说明理由.
(第19题图) 备用图
解:(1)证明:如答图①,连结BC,
第19题答图①
∵ AC=BD,∴∠ECB=∠EBC,
∵OB=OC,∴∠OCB=∠OBC,
∴∠ECF=∠ECB-∠OCB=∠EBC-∠OBC=∠OBA,即∠OBA=∠OCD;
(2)∵OA=OB,∴∠OAF=∠OBA,
∴∠OAF=∠ECF,
①当∠AFO=90°时,
∵OA=,tan∠OBA=,
∴OC=OA=,OF=1,AB=4,
∴EF=CF·tan∠ECF= CF·tan∠OBA=;
②当∠AOF =90°时,
∵OA=OB,∴∠OAF=∠OBA,
∴tan∠OAF= tan∠OBA=,
∵OA=,∴OF= OA·tan∠OAF=,
∴AF=,CF=,
∵∠OAF=∠OBA=∠ECF,∠OFA=∠EFC,
∴△OFA∽△EFC,
∴EF=·OF=·=,
综上所述EF=或;
(3)存在,如答图②,连结OE,
第19题答图②
∵∠ECB=∠EBC,∴CE=EB,
∵OE=OE,OB=OC,
∴△OEC≌△OEB,
∵ S△CEF=4S△BOF,
∴ S△CEO+S△FEO=4(S△BEO-S△EFO),
∴=,∴=,∴FO=CO=,
∵△OFA∽△EFC,∴===,
∴BF=BE-EF=CE-EF=EF,
∴AF=AB-BF=4-EF,
∵△OFA∽△EFC,
∴=,即=,
解得EF=3+>4(舍去)或EF=3-.
∴EF=3-.
(教材P93作业题第6题)
如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上任意一点,连结AD,GD.找出图中和∠ADC相等的角,并给出证明.
(教材母题图)
解:∠G=∠ADC,
证明:连结AC,
∵AB是圆O的直径,弦CD⊥AB,
∴AB垂直平分CD,∴=,
∴∠G=∠ADC.
垂径定理、圆心角定理圆周角定理的综合运用
1.[金华校级期中]如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,则CD的长为( )
(第1题图)
A.2 B.4
C.4 D.8
2.[嘉兴校级期中]如图,在Rt△ABC中,∠ACB=90°,AC=3,BC= 4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
A. B. C. D.
(第2题图)
3.[杭州余杭区期末]如图,已知⊙O的半径为10,AB⊥CD,垂足为P,且AB=CD=16,则OP的长为( )
(第3题图)
A.6 B.6
C.8 D.8
4.[金华校级期中]如图,已知⊙O是等腰直角三角形ABC的外接圆,点D是上一点,BD交AC于点E,若BC=4,AD=,则AE的长是( )
(第4题图)
A.3 B.2
C.1 D.1.2
在Rt△BCE中,CE2+BC2=BE2,即(4-AE)2+42=(5AE)2,解得AE=1.
5.[杭州西湖区校级期中]有一座圆弧形的拱桥,桥下水面宽24 m,拱顶高出水平面8 m,现有一货船,送一箱货欲从桥下经过,已知货箱(货箱底与水平面持平)宽10 m,至多能载货物的高为( )
A.4 m B.5 m
C.6 m D.7 m
6.[诸暨校级期中]如图,△ABC内接于⊙O,BC=a,AC=b,∠A-∠B=90°,则⊙O的面积为____.
(第6题图)
7.[湖州吴兴区期中]如图,A,B,C,D是⊙O上的四个点,若+=+,且弦AB=8,CD=4,则⊙O的半径为____.
(第7题图)
圆的基本性质与全等三角形的综合
8.[慈溪期中]如图,BC=2,A为半径为1的圆B上一点,连结AC,在AC上方作一个正三角形ACD,连结BD,则BD的最大值为___.
(第8题图)
9.[杭州西湖区校级期中]如图,在⊙O中,弦AC,BD相交于点M,且∠OAC=∠OBD.
(1)求证:AC=BD;
(2)若OA=4,∠OAC=30°,当AC⊥BD时,求:
①图中阴影部分面积;
②弧CD的长.
(第9题图)
10.[杭州江干区期末]如图,⊙O是△ABC的外接圆,AC是直径,过O作OD∥BC交AB于点D.延长DO交⊙O于点E,作EF⊥AC于点F,连结DF并延长交直线BC于点G,连结EG.
(1)求证:FC=GC;
(2)四边形EDBG是哪种特殊四边形?请说明理由.
(第10题图)
圆与内、外角平分线问题
11.[杭州萧山区校级期中]如图,AD是△ABC外角∠EAC的平分线,AD与△ABC的外接圆相交于点D,图中所有与∠DCB相等的角的个数为( )
(第11题图)
A.1 B.2
C.3 D.4
12.[杭州萧山区校级期中]如图,在⊙O中,AD平分圆周角∠BAC,∠BAC=60°,∠OAD=16°,∠C的度数为( )
A.50° B.30°
C.44° D.45°
(第12题图)
13.[宁波鄞州区校级期中]如图,在⊙O中,圆周角∠BAC=60°,弦AD平分∠BAC,AB=4,AC=3,则AD的长为___.
(第13题图)
圆的基本性质与相似三角形
14.[杭州校级期中]如图,△ABC内接⊙O,AD⊥BC于D,AE是⊙O的直径.若AB=6,AC=9,AE=11.
(第14题图)
(1)求证:△ABD∽△AEC;
(2)求AD的长.
15.[衢州校级期中]如图,已知AB为⊙O的直径,弦BE=DE,且AD,BE的延长线交于点C.
(1)求证:AC=AB;
(2)若CE=2,CD=,求⊙O的直径.
(第15题图)
16.[杭州校级期中]如图,AB为⊙O的直径,弦CD⊥AB于点E,点G是上一点,连结AC,AG,CG.
(1)在不添辅助线的前提下直接写出图中与∠AGC相等的角,不用证明;
(2)求证:当AB∥DG时,△ACG与△EAC相似;
(第16题图) 备用图
(3)若OE=BE,求∠AGC的度数.
17.[杭州校级期中]如图,已知A,P,B,C是⊙O上的四点,∠APC=∠BPC=60°,AB与PC交于Q点.
(1)判断△ABC 的形状,并证明你的结论;
(2)直接写出所有与△APQ相似的三角形:__ __;
(3)若AP=6,=,求PB的长.
(第17题图)
圆的综合探究
18.[杭州余杭区期末]已知:如图,AB是圆O的直径,CD是圆O的弦,AB⊥CD,E为垂足,AE=CD=8,F是CD延长线上一点,连结AF交圆O于G,连结AD,DG.
(1)求圆O的半径;
(2)求证:△ADG∽△AFD;
(3)当点G是弧AD的中点时,求△ADG的面积与△AFD的面积之比.
(第18题图)
19.[宁波北仑区期末]如图,在⊙O中,弦AB,CD相交于点E,=,点D在上,连结CO,并延长CO交线段AB于点F,连结OA,OB,且OA=,tan∠OBA=.
(1)求证:∠OBA=∠OCD;
(2)当△AOF是直角三角形时,求EF的长;
(3)是否存在点F,使得S△CEF=4S△BOF,若存在,请求出EF的长;若不存在,请说明理由.
(第19题图) 备用图
答案
垂径定理、圆心角定理圆周角定理的综合运用
1.[金华校级期中]如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,则CD的长为( C )
(第1题图)
A.2 B.4
C.4 D.8
解:∵∠A=22.5°,
∴∠BOC=2∠A=45°,
∵⊙O的直径AB垂直于弦CD,
∴CE=DE,△OCE为等腰直角三角形,
∴CE=OC=2,
∴CD=2CE=4.
2.[嘉兴校级期中]如图,在Rt△ABC中,∠ACB=90°,AC=3,BC= 4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( C )
A. B. C. D.
(第2题图) 第2题答图
解:过C作CM⊥AB,交AB于点M,如答图所示,
∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB==5,
∵CM⊥AB,∴M为AD的中点,
∵S△ABC=AC·BC=AB·CM,且AC=3,BC=4,AB=5,∴CM=,
在Rt△ACM中,AC2=AM2+CM2,即32=AM2+,解得AM=,∴AD=2AM=.
3.[杭州余杭区期末]如图,已知⊙O的半径为10,AB⊥CD,垂足为P,且AB=CD=16,则OP的长为( B )
(第3题图)
A.6 B.6
C.8 D.8
【解析】 作OM⊥AB于M,ON⊥CD于N,连结OB,OD,
∵AB=CD=16,∴BM=DN=8,
∴OM=ON==6,
∵AB⊥CD,OM⊥AB,ON⊥CD,
∴四边形MONP是正方形,
∴OP==6.故选B.
4.[金华校级期中]如图,已知⊙O是等腰直角三角形ABC的外接圆,点D是上一点,BD交AC于点E,若BC=4,AD=,则AE的长是( C )
(第4题图)
A.3 B.2
C.1 D.1.2
解:在等腰直角三角形ABC中,BC=4,
∴AB是⊙O的直径,AC=4,∴∠D=90°,
∵∠D=∠C,∠DAC=∠CBE,
∴△ADE∽△BCE,
∴==,即BE=5AE,
在Rt△BCE中,CE2+BC2=BE2,即(4-AE)2+42=(5AE)2,解得AE=1.
5.[杭州西湖区校级期中]有一座圆弧形的拱桥,桥下水面宽24 m,拱顶高出水平面8 m,现有一货船,送一箱货欲从桥下经过,已知货箱(货箱底与水平面持平)宽10 m,至多能载货物的高为( D )
A.4 m B.5 m
C.6 m D.7 m
解:如答图,表示桥拱,AB=24 m,CD=8 m,EF=10 m,D为AB,EF的中点,且CD,ME,NF均垂直于AB,
第5题答图
设所在圆的圆心为O,连结OA,ON,设OA=R,
则OD=OC-DC=R-8,AD=AB=12 m,
又∵OA2=AD2+OD2,
即R2=122+(R-8)2,解得R=13(m).
在Rt△ONG中,由勾股定理得,OG==12 m,
∴FN=DG=OG-OD=OG-(OC-CD)=7 m.故选D.
6.[诸暨校级期中]如图,△ABC内接于⊙O,BC=a,AC=b,∠A-∠B=90°,则⊙O的面积为__(a2+b2)__.
(第6题图) 第6题答图
【解析】 如答图,过点B作圆的直径BE交圆于点E,则∠ECB=90°,
∴∠E+∠EBC=90°,
又∵圆内接四边形的对角互补,即∠E+∠A=180°,∴∠A-∠EBC=90°,
∵∠A-∠ABC=90°,∴∠CBA=∠CBE,
∴弧AC=弧CE,∴CE=AC=b,
由勾股定理得,BE=,
∴⊙O的半径=,
∴圆的面积=(a2+b2).
7.[湖州吴兴区期中]如图,A,B,C,D是⊙O上的四个点,若+=+,且弦AB=8,CD=4,则⊙O的半径为__2__.
(第7题图) 第7题答图
【解析】 如答图,连结BO并延长,与圆交于E,连结AE,
+=+,所以AB,CD所对圆心角之和是180°,
∴CD=AE,∠A=90°,
BE===4,
∴半径是2.
圆的基本性质与全等三角形的综合
8.[慈溪期中]如图,BC=2,A为半径为1的圆B上一点,连结AC,在AC上方作一个正三角形ACD,连结BD,则BD的最大值为__3__.
(第8题图) 第8题答图
【解析】 如答图,将BC绕点C顺时针旋转60°到点M,连结MD,MB,当点B,M,D共线时,BD有最大值,
∵∠BCM=60°,CM=BC=2,
∴△BCM是等边三角形,∴BM=2,
∵∠BCM=∠ACD=60°,∴∠ACB=∠MCD,
∵AC=CD,BC=CM,
∴△ABC≌△DMC,∴DM=AB=1,
∴BD=3.
9.[杭州西湖区校级期中]如图,在⊙O中,弦AC,BD相交于点M,且∠OAC=∠OBD.
(1)求证:AC=BD;
(2)若OA=4,∠OAC=30°,当AC⊥BD时,求:
①图中阴影部分面积;
②弧CD的长.
(第9题图) 第9题答图
解:(1)连结OC,OD,
∵OA=OC,∴∠CAO=∠ACO,
∵OD=OB,∴∠ODB=∠OBD,
∵ ∠OAC=∠OBD,∴∠CAO=∠ACO=∠ODB=∠OBD,
∵
∴△OAC≌△ODB(AAS),∴AC=BD;
(2)如答图,作ON⊥AC于N,OP⊥BD于P,连结OM,
由(1)可知AC=BD,∴ON=OP,
∵AC⊥BD,OP⊥BD,ON⊥AC,ON=OP,
∴四边形OPMN是正方形,
∴∠AMO=∠BMO=45°,
∵
∴△AMO≌△BMO,∴S△AMO=S△BMO,
∵OA=4,∠OAC=30°,
∴ON=2,AN=2,MN=2,
∵∠MOA=45°+60°=105°,
∴∠AOB=360°-105°×2=150°;
①S阴影=S扇AOB+ 2S△AOM
=×πr2+2××(2+2)×2=+4+4;
②∠DOC=∠AOC+∠DOB+∠AOB-360°=30°,
∴=×2πr=π.
10.[杭州江干区期末]如图,⊙O是△ABC的外接圆,AC是直径,过O作OD∥BC交AB于点D.延长DO交⊙O于点E,作EF⊥AC于点F,连结DF并延长交直线BC于点G,连结EG.
(1)求证:FC=GC;
(2)四边形EDBG是哪种特殊四边形?请说明理由.
(第10题图) 第10题答图
解:(1)证明:∵AC为直径,∴∠B=90°,
∵OD∥BC,∴∠ADO=∠B=90°,
在△AOD和△EOF中,
∴△AOD≌△EOF,∴OD=OF,
∴∠ODF=∠OFD,
∵OD∥BC,∴∠FGC=∠ODF,
又∵∠GFC=∠OFD,∴∠CFG=∠FGC,
∴FC=GC;
(2)四边形EDBG是矩形,理由如下:
如答图,连结AE,EC,
∵OA=OE,∴∠OAE=∠OEA,
∵OD=OF,∴∠ODF=∠OFD,
∴∠OAE=∠OFD,∴AE∥DG,
∵AC为直径,∴∠AEC=90°,
又∵CF=CG,∴CE是FG的垂直平分线,
∴△EFC≌△EGC,
∴∠EGC=∠EFC=90°,
又∵∠EDB=90°,∠ABC=90°,
∴四边形EDBG是矩形.
圆与内、外角平分线问题
11.[杭州萧山区校级期中]如图,AD是△ABC外角∠EAC的平分线,AD与△ABC的外接圆相交于点D,图中所有与∠DCB相等的角的个数为( C )
(第11题图)
A.1 B.2
C.3 D.4
【解析】 ∵A,B,C,D四点共圆,
∴∠DCB=∠EAD,
∵AD是△ABC外角∠EAC的平分线,
∴∠EAD=∠CAD=∠EAC,
∴∠EAD=∠CAD=∠BCD=∠DBC.故选C.
12.[杭州萧山区校级期中]如图,在⊙O中,AD平分圆周角∠BAC,∠BAC=60°,∠OAD=16°,∠C的度数为( C )
A.50° B.30°
C.44° D.45°
(第12题图) 第12题答图
【解析】 如答图,连结OD,CD,
∵OA=OD,∴∠OAD=∠ODA=16°,
∴∠AOD=148°,∴∠ACD=74°,
∵∠BAC=60°,AD平分圆周角∠BAC,
∴∠BAD=30°,∴∠BCD=30°,
∴∠ACB=∠ACD-∠BCD=44°.
13.[宁波鄞州区校级期中]如图,在⊙O中,圆周角∠BAC=60°,弦AD平分∠BAC,AB=4,AC=3,则AD的长为____.
(第13题图) 第13题答图
【解析】 如答图,连结BD,CD,过点B作BN⊥AD于N,过点C作CM⊥AD于M.
∵∠BAC=60°,AD平分∠BAC,
∴∠BAD=∠CAD=30°,
∵AB=4,∠BAD=30°,BN⊥AD,
∴BN=2,AN=2,
∵AC=3,∠CAD=30°,CM⊥AD,
∴CM=,AM=,∴MN=,
设DN=a,
∵∠BAD=∠CAD,∴BD=CD,
由勾股定理得BN2+DN2=CM2+DM2,即22+a2=+,
解得a=,∴AD=AN+DN=.
圆的基本性质与相似三角形
14.[杭州校级期中]如图,△ABC内接⊙O,AD⊥BC于D,AE是⊙O的直径.若AB=6,AC=9,AE=11.
(第14题图)
(1)求证:△ABD∽△AEC;
(2)求AD的长.
解:(1)证明:∵AE是⊙O的直径,AD⊥BC,
∴∠ACE=∠ADB=90°,
∵∠E=∠B,∴△ABD∽△AEC;
(2)∵△ABD ∽△AEC,∴=,
∵AB=6,AC=9,AE=11,∴AD=.
15.[衢州校级期中]如图,已知AB为⊙O的直径,弦BE=DE,且AD,BE的延长线交于点C.
(1)求证:AC=AB;
(2)若CE=2,CD=,求⊙O的直径.
(第15题图) 第15题答图
解:(1)证明:如答图,连结AE,
∵AB为⊙O的直径,
∴∠AEB=90°,∴∠AEB=∠AEC=90°,
∵BE=DE,
∴=,∴∠DAE=∠BAE,
∵∠C=90°-∠DAE,∠B=90°-∠BAE,
∴∠B=∠C,∴AC=AB;
(2)∵∠C=∠C,∠CED=∠CAB,
∴△CDE∽△CBA,∴=,
∴CD·CA=CB·CE,∴×AC=2×4,
∴AC=.∴⊙O的直径为.
16.[杭州校级期中]如图,AB为⊙O的直径,弦CD⊥AB于点E,点G是上一点,连结AC,AG,CG.
(1)在不添辅助线的前提下直接写出图中与∠AGC相等的角,不用证明;
(2)求证:当AB∥DG时,△ACG与△EAC相似;
(第16题图) 备用图
(3)若OE=BE,求∠AGC的度数.
解:(1)结论:∠ACE=∠AGC.
(2)证明:∵DG∥AB,
第16题答图
∴∠AEC=∠CDG=90°,
∴CG是直径,∴∠CAG=90°,
∵∠CAG=∠AEC=90°,∠AGC=∠ACE,
∴△ACG∽△EAC.
(3)如答图,连结OC,BC.
∵OE=EB,CE⊥OB,
∴CO=CB=OB,
∴△OBC是等边三角形,
∴∠B=60°,∴∠AGC=∠B=60°.
17.[杭州校级期中]如图,已知A,P,B,C是⊙O上的四点,∠APC=∠BPC=60°,AB与PC交于Q点.
(1)判断△ABC 的形状,并证明你的结论;
(2)直接写出所有与△APQ相似的三角形:__△CBQ和△CPB__;
(3)若AP=6,=,求PB的长.
(第17题图) 第17题答图
解:(1)△ABC是等边三角形.
∵∠BPC=∠APC=60°,∠BAC=∠ABC=60°,
∴△ABC是等边三角形;
(2)△CBQ和△CPB.
(3)如答图,过B作BD∥PA交PC于D,
则∠BDP=∠APC=60°.
又∵∠AQP=∠BQD,
∴△AQP∽△BQD,∴=,
∵∠BPD=∠BDP=60°,∴PB=BD.
∴=,∴=,∴PB=10.
圆的综合探究
18.[杭州余杭区期末]已知:如图,AB是圆O的直径,CD是圆O的弦,AB⊥CD,E为垂足,AE=CD=8,F是CD延长线上一点,连结AF交圆O于G,连结AD,DG.
(1)求圆O的半径;
(2)求证:△ADG∽△AFD;
(3)当点G是弧AD的中点时,求△ADG的面积与△AFD的面积之比.
(第18题图) 第18题答图
解:(1)如答图,连结OC,设⊙O的半径为R,
∵AE=8,∴OE=8-R,
∵直径AB⊥CD,
∴∠CEO=90°,CE=CD=4,
在Rt△CEO中,根据勾股定理得,R2-(8-R)2=16,∴R=5,
即⊙O的半径为5;
(2)如答图,连结BG,
∴∠ADG=∠ABG,
∵AB是⊙O的直径,∴∠AGB=90°,
∴∠ABG+∠BAG=90°,
∴∠ADG+∠BAG=90°,
∵AB⊥CD,∴∠BAG+∠F=90°,
∴∠ADG=∠F,
∵∠DAG=∠FAD,∴△ADG∽△AFD;
(3)如答图,连结OG交AD于H,
在Rt△ADE中,AE=8,DE=CD=4,根据勾股定理得,AD=4,
∵点G是的中点,
∴AH=AD=2,OG⊥AD,
在Rt△AOH中,根据勾股定理得,OH=,
在Rt△AHG中,HG=OG-OH=5-,根据勾股定理得,AG2=AH2+HG2=50-10,
由(2)知,△ADG∽△AFD,
∴===.
19.[宁波北仑区期末]如图,在⊙O中,弦AB,CD相交于点E,=,点D在上,连结CO,并延长CO交线段AB于点F,连结OA,OB,且OA=,tan∠OBA=.
(1)求证:∠OBA=∠OCD;
(2)当△AOF是直角三角形时,求EF的长;
(3)是否存在点F,使得S△CEF=4S△BOF,若存在,请求出EF的长;若不存在,请说明理由.
(第19题图) 备用图
解:(1)证明:如答图①,连结BC,
第19题答图①
∵ AC=BD,∴∠ECB=∠EBC,
∵OB=OC,∴∠OCB=∠OBC,
∴∠ECF=∠ECB-∠OCB=∠EBC-∠OBC=∠OBA,即∠OBA=∠OCD;
(2)∵OA=OB,∴∠OAF=∠OBA,
∴∠OAF=∠ECF,
①当∠AFO=90°时,
∵OA=,tan∠OBA=,
∴OC=OA=,OF=1,AB=4,
∴EF=CF·tan∠ECF= CF·tan∠OBA=;
②当∠AOF =90°时,
∵OA=OB,∴∠OAF=∠OBA,
∴tan∠OAF= tan∠OBA=,
∵OA=,∴OF= OA·tan∠OAF=,
∴AF=,CF=,
∵∠OAF=∠OBA=∠ECF,∠OFA=∠EFC,
∴△OFA∽△EFC,
∴EF=·OF=·=,
综上所述EF=或;
(3)存在,如答图②,连结OE,
第19题答图②
∵∠ECB=∠EBC,∴CE=EB,
∵OE=OE,OB=OC,
∴△OEC≌△OEB,
∵ S△CEF=4S△BOF,
∴ S△CEO+S△FEO=4(S△BEO-S△EFO),
∴=,∴=,∴FO=CO=,
∵△OFA∽△EFC,∴===,
∴BF=BE-EF=CE-EF=EF,
∴AF=AB-BF=4-EF,
∵△OFA∽△EFC,
∴=,即=,
解得EF=3+>4(舍去)或EF=3-.
∴EF=3-.
同课章节目录
