4.2 代数式(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 4.2 代数式(知识清单+经典例题+夯实基础+提优特训+中考链接) |  | |
| 格式 | zip | ||
| 文件大小 | 299.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-08 10:40:46 | ||
图片预览


文档简介
浙江版2019-2020学年度七年级数学上册第4章代数式
4.2 代数式
【知识清单】
1.概念:由数、表示数的字母和运算符号组成的数学表达式称为代数式,这里的运算是指加、减、乘、除、乘方和开方.特别规定:单独一个数或者一个字母也称为代数式
2.意义:代数式可以简明地、具有普遍意义地表示实际问题中的量
3.列代数式:特别注意找规律这种类型的题目.
4.注意:用代数式表示具有实际意义的量时,如果所列的代数式是“和”或“差”的形式,并且有单位,那么必须把所列代数式用括号括起来,后面写上单位,如:温度由t℃下降2℃后所列代数式为(t2)℃.
【经典例题】
例题1、如图两同心圆,大圆半径为R,小圆半径为r,则阴影部分的面积为( )
A. πR2 B. πr2 C. π(R2+r2) D. π(R2r2)
【考点】列代数式.
【分析】阴影部分的面积=大圆的面积-小圆的面积,把相关数值代入即可.
【解答】∵大圆的面积为πR2,小圆的面积为πr2,
∴阴影部分的面积为πR2πr2=π(R2r2),
故选D.
【点评】考查列代数式解决图形面积问题,得到圆环的面积的等量关系是解决本题的关键.
例题2、用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第n个图形需____根火柴棒.
【考点】列代数式.规律型:图形的变化类.?
【分析】对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目中的难点.
【解答】根据题意分析可得:
第一个图形用了12根火柴;即12=6(1+1);
第二个图形用了18根火柴;即18=6(2+1);
第三个图形用了18根火柴;即18=6(3+1)
…
按照这种方式搭下去,搭第n个图形需6(n+1)根火柴.
【点评】本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.
【夯实基础】
1、下列各式中是代数式的个数为?( )
① ;②2x+3y5; ③S=πR2;④;⑤ x>y;⑥2mn;⑦ab.
A.7 B.6 C.5 D.4
2、设乙数为a,甲数比乙数小32%,用代数式表示甲数,正确的是( )
A.a0.68 B.a0.32a C.0.32a D.10.32a
3、某市2019年7月份某日的一天的温差为10 ℃,最高温度为t ℃,则最低气温可表示
为 ( )
A.(t10) ℃ B.(10t) ℃ C.(10t) ℃ D.(t+10) ℃
4、把代数式“”用文字语言叙述,其中表述不正确的是( C )
A.比x的倒数的相反数大6的数 B.x的倒数的相反数与6的和
C.x的倒数与6的和 D.6与x的倒数的差
5、某公园门票票价为成人每张a元,儿童门票为成人的一半,,如果某天公园卖出x张成人票,y张儿童票,那么这一天公园的门票收入为 元.
6、学校购买了一批图书,共a箱,每箱有b册,学校决定将这批图书的捐给社会福利院,又将剩余图书的奖励给优秀学生,则的图书为 册.(用含a、b的代数式表示)
7、观察下列一组图形中点的个数,其中第1个图中共有5个点,第2个图中共有13 个点,第3个图中共有25 个点,…, 按此规律第4个图中共有点数 个;第n个图中共有点的个数为 ?个.
8、列式表示:
(1)a的5倍与y的三分之一的差;
(2)m与n的差的立方与m,n的积的商;
(3)比2x与3y的和的6倍小3的数;
(4)a的一半与b的四分之一差的.
9、甲、乙两人从同一地点出发,甲每小时走5千米,乙每小时走3千米,用代数式表示:
(1)若两人反向行走th,两人相距多远?
(2)若两人同向行走th,两人相距多远?
(3)反向行走,甲比乙早出发m小时,乙走n小时,两人相距多少米?
(4)同向行走,甲比乙晚出发m小时,乙走n小时(n>m),两人相距多少米?
【提优特训】
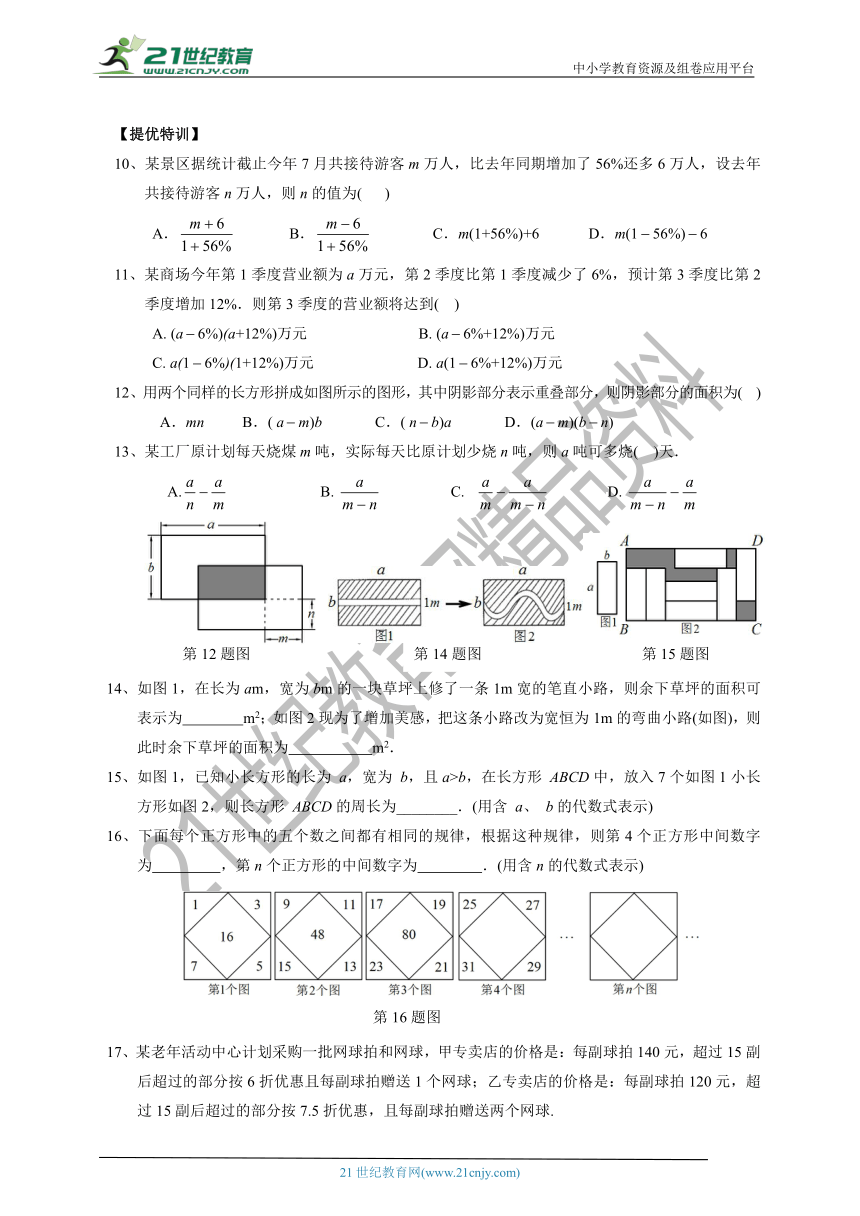
10、某景区据统计截止今年7月共接待游客m万人,比去年同期增加了56%还多6万人,设去年共接待游客n万人,则n的值为( )
A. B. C.m(1+56%)+6? D.m(156%)6
11、某商场今年第1季度营业额为a万元,第2季度比第1季度减少了6%,预计第3季度比第2季度增加12%.则第3季度的营业额将达到(?? )
A.?(a6%)(a+12%)万元?????????????????????????????B.?(a6%+12%)万元
C.?a(16%)(1+12%)万元???????????????????????????D.?a(16%+12%)万元
12、用两个同样的长方形拼成如图所示的图形,其中阴影部分表示重叠部分,则阴影部分的面积为( )
A.mn B.( am)b C.( nb)a D.(am)(bn)
13、某工厂原计划每天烧煤m吨,实际每天比原计划少烧n吨,则a吨可多烧(????)天.
A.?????????????????????B.???????????????????C.? ???????????????D.?
14、如图1,在长为am,宽为bm的一块草坪上修了一条1m宽的笔直小路,则余下草坪的面积可表示为 m2;如图2现为了增加美感,把这条小路改为宽恒为1m的弯曲小路(如图),则此时余下草坪的面积为 m2.
15、如图1,已知小长方形的长为 a,宽为 b,且a>b,在长方形 ABCD中,放入7个如图1小长方形如图2,则长方形 ABCD的周长为________.(用含 a、 b的代数式表示)
16、下面每个正方形中的五个数之间都有相同的规律,根据这种规律,则第4个正方形中间数字为 ,第n个正方形的中间数字为 ?.(用含n的代数式表示)
17、某老年活动中心计划采购一批网球拍和网球,甲专卖店的价格是:每副球拍140元,超过15副后超过的部分按6折优惠且每副球拍赠送1个网球;乙专卖店的价格是:每副球拍120元,超过15副后超过的部分按7.5折优惠,且每副球拍赠送两个网球.
18、用代数式表示:(1)一个两位数的个位数为a,十位数为7,请用代数式表示这个两位数;
(2)一个两位数的个位数为a,十位数为b,请用代数式表示这个两位数;
(3)a,b都是两位数,b放在a的左边,得到的四位数该怎样表示? a放在b的左边呢?
19、计算(1);
(2).
20、如图,是某住宅的平面结构图,图中标注有关尺寸(墙体厚度忽略不计,尺寸单位:米),房子的主人计划把卧室以外的地面都铺上瓷砖.题目的结果(用含a、x、y的代数式表示).
(1)请你帮他计算一下要铺瓷砖的面积是多少?
(2)如果选用瓷砖的价格是m元/平方米,
问他买瓷砖需用多少钱?
【中考链接】
21、(2018?枣庄)如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长2b的小正方形后,再将剩下的三块拼成一块矩形,
则这块矩形较长的边长为( )
A.3a+2b B.3a+4b
C.6a+2b D.6a+4b
22、(2018?桂林)用代数式表示:a的2倍与3的和.下列表示正确的是( )
A.2a3 B.2a+3 C.2(a3) D.2(a+3)
23、(2018?安徽)据省统计局发布,2017年我省有效发明专利数比2016年增长22.1%.假定2018年的年增长率保持不变,2016年和2018年我省有效发明专利分别为a万件和b万件,则( )
A.b=(1+22.1%×2)a B.b=(1+22.1%)2a C.b=(1+22.1%)×2a D.b=22.1%×2a
24、(2018?成都)已知a>0,S1=,S2=S11,S3=,S4=S31,S5=,…(即当n为大于1的奇数时,Sn=;当n为大于1的偶数时,Sn=Sn-11),按此规律,S2018= .
参考答案
1、C 2、B 3、A 4、C 5、ax+y 6、[(ab)(ab)] 7、41, 10、B 11、C 12、D 13、D 14、a(b1),a(b1) 15、3a+6b 16、112,(8n1)(8n5) (8n7)(8n3) 21、A 22、B 23、 B 24、
23、B 24、B
8、列式表示:
(1)a的5倍与y的三分之一的差;
(2)m与n的差的立方与m,n的积的商;
(3)比2x与3y的和的6倍小3的数;
(4)a的一半与b的四分之一差的.
解:(1)5a-;(2);(3)6(2x+3y)-3;(4).
9、甲、乙两人从同一地点出发,甲每小时走5千米,乙每小时走3千米,用代数式表示:
(1)若两人反向行走th,两人相距多远?
(2)若两人同向行走th,两人相距多远?
(3)反向行走,甲比乙早出发m小时,乙走n小时,两人相距多少米?
(4)同向行走,甲比乙晚出发m小时,乙走n小时(n>m),两人相距多少米?
解:
(1) s=(5+3)t
(2) s= (53)t
(3) s=5m+8n
(4) s=|5m2n|
17、某老年活动中心计划采购一批网球拍和网球,甲专卖店的价格是:每副球拍140元,超过15副后超过的部分按6折优惠且每副球拍赠送1个网球;乙专卖店的价格是:每副球拍120元,超过15副后超过的部分按7.5折优惠,且每副球拍赠送两个网球.
求如果老年活动中心要买x副球拍(不考虑网球的数量),那么在甲、乙两家卖点分别需要花多少钱(用含有x的式子表示).
解:当x≤15时:
甲店:140x,乙店:120x.
当x≥15时:
甲店:140×15+140×0.6(x15),乙店:120×15+120×0.75(x15).
18、用代数式表示:(1)一个两位数的个位数为a,十位数为7,请用代数式表示这个两位数;
(2)一个两位数的个位数为a,十位数为b,请用代数式表示这个两位数;
(3)a,b都是两位数,b放在a的左边,得到的四位数该怎样表示? a放在b的左边呢?
解:(1)70+a (2)10b+a (3)100b+a 100a+b
19、计算(1);
(2).
解:(1)原式=
=
=
(2)原式=
=
=2
=2
=2
=2=.
20、如图,是某住宅的平面结构图,图中标注有关尺寸(墙体厚度忽略不计,尺寸单位:米),房子的主人计划把卧室以外的地面都铺上瓷砖.题目的结果(用含a、x、y的代数式表示).
(1)请你帮他计算一下要铺瓷砖的面积是多少?
(2)如果选用瓷砖的价格是m元/平方米,
问他买瓷砖需用多少钱?
解:(1)根据该住宅的平面结构示意图,可知:
主卧、中间的公共部分、次卧的面积为:(1.6x+0.2x+1.5x?)0.8y?=?2.64xy?;
阳台、次卧、中间的公共部分、卫生间的面积为:??(1.75?x+0.2x?+1.5x?)y =3.45xy?;
客厅的面积为:1.75x(3.2y0.8yy)?=2.45xy?;
餐厅、厨房的面积为:(3.6x1.75x)1.2y=2.22xy.
因此需要瓷砖的面积应该是2.64xy?+3.45xy?+2.45xy?+2.22xy =10.76xy?;
(2)∵瓷砖的价格是m?元/平方米,
∴买瓷砖至少需用10.76mxy?元.
4.2 代数式
【知识清单】
1.概念:由数、表示数的字母和运算符号组成的数学表达式称为代数式,这里的运算是指加、减、乘、除、乘方和开方.特别规定:单独一个数或者一个字母也称为代数式
2.意义:代数式可以简明地、具有普遍意义地表示实际问题中的量
3.列代数式:特别注意找规律这种类型的题目.
4.注意:用代数式表示具有实际意义的量时,如果所列的代数式是“和”或“差”的形式,并且有单位,那么必须把所列代数式用括号括起来,后面写上单位,如:温度由t℃下降2℃后所列代数式为(t2)℃.
【经典例题】
例题1、如图两同心圆,大圆半径为R,小圆半径为r,则阴影部分的面积为( )
A. πR2 B. πr2 C. π(R2+r2) D. π(R2r2)
【考点】列代数式.
【分析】阴影部分的面积=大圆的面积-小圆的面积,把相关数值代入即可.
【解答】∵大圆的面积为πR2,小圆的面积为πr2,
∴阴影部分的面积为πR2πr2=π(R2r2),
故选D.
【点评】考查列代数式解决图形面积问题,得到圆环的面积的等量关系是解决本题的关键.
例题2、用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第n个图形需____根火柴棒.
【考点】列代数式.规律型:图形的变化类.?
【分析】对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目中的难点.
【解答】根据题意分析可得:
第一个图形用了12根火柴;即12=6(1+1);
第二个图形用了18根火柴;即18=6(2+1);
第三个图形用了18根火柴;即18=6(3+1)
…
按照这种方式搭下去,搭第n个图形需6(n+1)根火柴.
【点评】本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.
【夯实基础】
1、下列各式中是代数式的个数为?( )
① ;②2x+3y5; ③S=πR2;④;⑤ x>y;⑥2mn;⑦ab.
A.7 B.6 C.5 D.4
2、设乙数为a,甲数比乙数小32%,用代数式表示甲数,正确的是( )
A.a0.68 B.a0.32a C.0.32a D.10.32a
3、某市2019年7月份某日的一天的温差为10 ℃,最高温度为t ℃,则最低气温可表示
为 ( )
A.(t10) ℃ B.(10t) ℃ C.(10t) ℃ D.(t+10) ℃
4、把代数式“”用文字语言叙述,其中表述不正确的是( C )
A.比x的倒数的相反数大6的数 B.x的倒数的相反数与6的和
C.x的倒数与6的和 D.6与x的倒数的差
5、某公园门票票价为成人每张a元,儿童门票为成人的一半,,如果某天公园卖出x张成人票,y张儿童票,那么这一天公园的门票收入为 元.
6、学校购买了一批图书,共a箱,每箱有b册,学校决定将这批图书的捐给社会福利院,又将剩余图书的奖励给优秀学生,则的图书为 册.(用含a、b的代数式表示)
7、观察下列一组图形中点的个数,其中第1个图中共有5个点,第2个图中共有13 个点,第3个图中共有25 个点,…, 按此规律第4个图中共有点数 个;第n个图中共有点的个数为 ?个.
8、列式表示:
(1)a的5倍与y的三分之一的差;
(2)m与n的差的立方与m,n的积的商;
(3)比2x与3y的和的6倍小3的数;
(4)a的一半与b的四分之一差的.
9、甲、乙两人从同一地点出发,甲每小时走5千米,乙每小时走3千米,用代数式表示:
(1)若两人反向行走th,两人相距多远?
(2)若两人同向行走th,两人相距多远?
(3)反向行走,甲比乙早出发m小时,乙走n小时,两人相距多少米?
(4)同向行走,甲比乙晚出发m小时,乙走n小时(n>m),两人相距多少米?
【提优特训】
10、某景区据统计截止今年7月共接待游客m万人,比去年同期增加了56%还多6万人,设去年共接待游客n万人,则n的值为( )
A. B. C.m(1+56%)+6? D.m(156%)6
11、某商场今年第1季度营业额为a万元,第2季度比第1季度减少了6%,预计第3季度比第2季度增加12%.则第3季度的营业额将达到(?? )
A.?(a6%)(a+12%)万元?????????????????????????????B.?(a6%+12%)万元
C.?a(16%)(1+12%)万元???????????????????????????D.?a(16%+12%)万元
12、用两个同样的长方形拼成如图所示的图形,其中阴影部分表示重叠部分,则阴影部分的面积为( )
A.mn B.( am)b C.( nb)a D.(am)(bn)
13、某工厂原计划每天烧煤m吨,实际每天比原计划少烧n吨,则a吨可多烧(????)天.
A.?????????????????????B.???????????????????C.? ???????????????D.?
14、如图1,在长为am,宽为bm的一块草坪上修了一条1m宽的笔直小路,则余下草坪的面积可表示为 m2;如图2现为了增加美感,把这条小路改为宽恒为1m的弯曲小路(如图),则此时余下草坪的面积为 m2.
15、如图1,已知小长方形的长为 a,宽为 b,且a>b,在长方形 ABCD中,放入7个如图1小长方形如图2,则长方形 ABCD的周长为________.(用含 a、 b的代数式表示)
16、下面每个正方形中的五个数之间都有相同的规律,根据这种规律,则第4个正方形中间数字为 ,第n个正方形的中间数字为 ?.(用含n的代数式表示)
17、某老年活动中心计划采购一批网球拍和网球,甲专卖店的价格是:每副球拍140元,超过15副后超过的部分按6折优惠且每副球拍赠送1个网球;乙专卖店的价格是:每副球拍120元,超过15副后超过的部分按7.5折优惠,且每副球拍赠送两个网球.
18、用代数式表示:(1)一个两位数的个位数为a,十位数为7,请用代数式表示这个两位数;
(2)一个两位数的个位数为a,十位数为b,请用代数式表示这个两位数;
(3)a,b都是两位数,b放在a的左边,得到的四位数该怎样表示? a放在b的左边呢?
19、计算(1);
(2).
20、如图,是某住宅的平面结构图,图中标注有关尺寸(墙体厚度忽略不计,尺寸单位:米),房子的主人计划把卧室以外的地面都铺上瓷砖.题目的结果(用含a、x、y的代数式表示).
(1)请你帮他计算一下要铺瓷砖的面积是多少?
(2)如果选用瓷砖的价格是m元/平方米,
问他买瓷砖需用多少钱?
【中考链接】
21、(2018?枣庄)如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长2b的小正方形后,再将剩下的三块拼成一块矩形,
则这块矩形较长的边长为( )
A.3a+2b B.3a+4b
C.6a+2b D.6a+4b
22、(2018?桂林)用代数式表示:a的2倍与3的和.下列表示正确的是( )
A.2a3 B.2a+3 C.2(a3) D.2(a+3)
23、(2018?安徽)据省统计局发布,2017年我省有效发明专利数比2016年增长22.1%.假定2018年的年增长率保持不变,2016年和2018年我省有效发明专利分别为a万件和b万件,则( )
A.b=(1+22.1%×2)a B.b=(1+22.1%)2a C.b=(1+22.1%)×2a D.b=22.1%×2a
24、(2018?成都)已知a>0,S1=,S2=S11,S3=,S4=S31,S5=,…(即当n为大于1的奇数时,Sn=;当n为大于1的偶数时,Sn=Sn-11),按此规律,S2018= .
参考答案
1、C 2、B 3、A 4、C 5、ax+y 6、[(ab)(ab)] 7、41, 10、B 11、C 12、D 13、D 14、a(b1),a(b1) 15、3a+6b 16、112,(8n1)(8n5) (8n7)(8n3) 21、A 22、B 23、 B 24、
23、B 24、B
8、列式表示:
(1)a的5倍与y的三分之一的差;
(2)m与n的差的立方与m,n的积的商;
(3)比2x与3y的和的6倍小3的数;
(4)a的一半与b的四分之一差的.
解:(1)5a-;(2);(3)6(2x+3y)-3;(4).
9、甲、乙两人从同一地点出发,甲每小时走5千米,乙每小时走3千米,用代数式表示:
(1)若两人反向行走th,两人相距多远?
(2)若两人同向行走th,两人相距多远?
(3)反向行走,甲比乙早出发m小时,乙走n小时,两人相距多少米?
(4)同向行走,甲比乙晚出发m小时,乙走n小时(n>m),两人相距多少米?
解:
(1) s=(5+3)t
(2) s= (53)t
(3) s=5m+8n
(4) s=|5m2n|
17、某老年活动中心计划采购一批网球拍和网球,甲专卖店的价格是:每副球拍140元,超过15副后超过的部分按6折优惠且每副球拍赠送1个网球;乙专卖店的价格是:每副球拍120元,超过15副后超过的部分按7.5折优惠,且每副球拍赠送两个网球.
求如果老年活动中心要买x副球拍(不考虑网球的数量),那么在甲、乙两家卖点分别需要花多少钱(用含有x的式子表示).
解:当x≤15时:
甲店:140x,乙店:120x.
当x≥15时:
甲店:140×15+140×0.6(x15),乙店:120×15+120×0.75(x15).
18、用代数式表示:(1)一个两位数的个位数为a,十位数为7,请用代数式表示这个两位数;
(2)一个两位数的个位数为a,十位数为b,请用代数式表示这个两位数;
(3)a,b都是两位数,b放在a的左边,得到的四位数该怎样表示? a放在b的左边呢?
解:(1)70+a (2)10b+a (3)100b+a 100a+b
19、计算(1);
(2).
解:(1)原式=
=
=
(2)原式=
=
=2
=2
=2
=2=.
20、如图,是某住宅的平面结构图,图中标注有关尺寸(墙体厚度忽略不计,尺寸单位:米),房子的主人计划把卧室以外的地面都铺上瓷砖.题目的结果(用含a、x、y的代数式表示).
(1)请你帮他计算一下要铺瓷砖的面积是多少?
(2)如果选用瓷砖的价格是m元/平方米,
问他买瓷砖需用多少钱?
解:(1)根据该住宅的平面结构示意图,可知:
主卧、中间的公共部分、次卧的面积为:(1.6x+0.2x+1.5x?)0.8y?=?2.64xy?;
阳台、次卧、中间的公共部分、卫生间的面积为:??(1.75?x+0.2x?+1.5x?)y =3.45xy?;
客厅的面积为:1.75x(3.2y0.8yy)?=2.45xy?;
餐厅、厨房的面积为:(3.6x1.75x)1.2y=2.22xy.
因此需要瓷砖的面积应该是2.64xy?+3.45xy?+2.45xy?+2.22xy =10.76xy?;
(2)∵瓷砖的价格是m?元/平方米,
∴买瓷砖至少需用10.76mxy?元.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
