1.1认识三角形(课时1) 同步训练(解析版)
文档属性
| 名称 | 1.1认识三角形(课时1) 同步训练(解析版) | 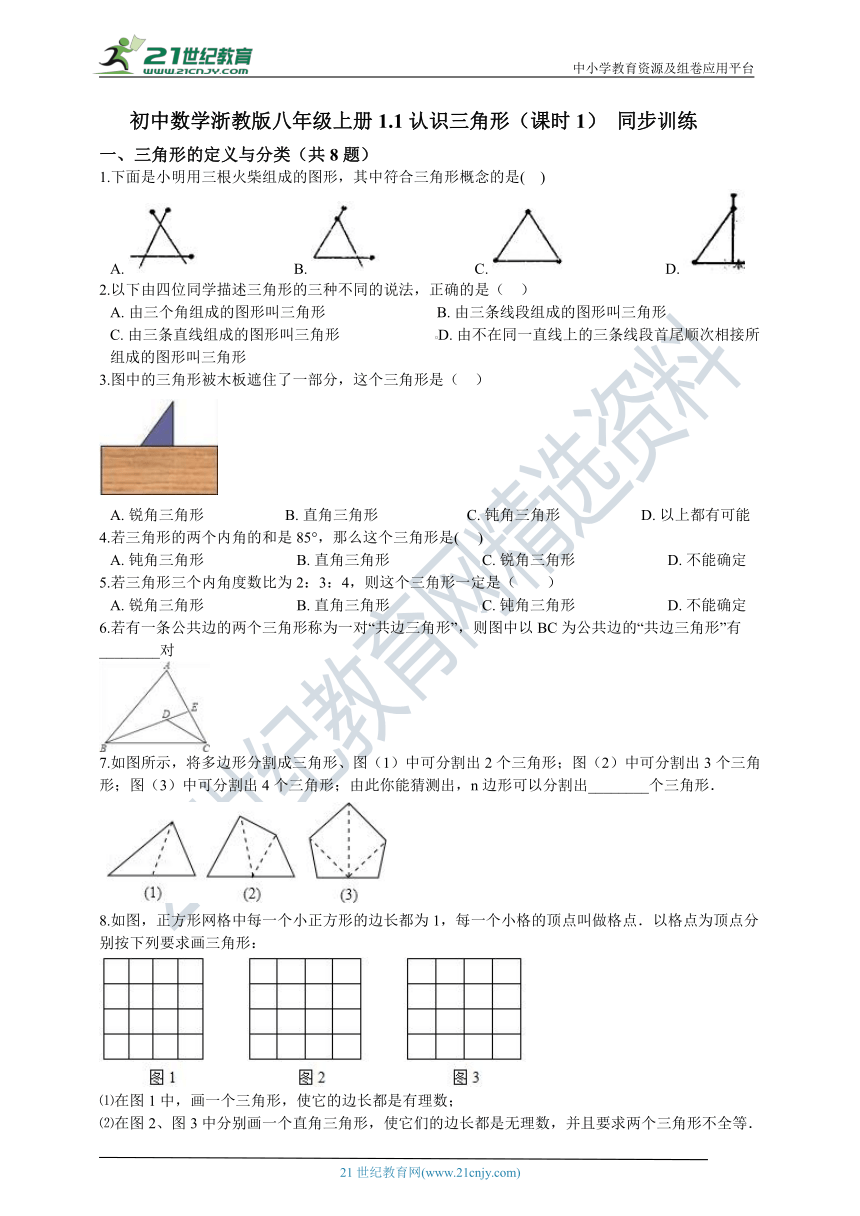 | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-09 18:48:53 | ||
图片预览




文档简介
初中数学浙教版八年级上册1.1认识三角形(课时1) 同步训练
一、三角形的定义与分类(共8题)
1.下面是小明用三根火柴组成的图形,其中符合三角形概念的是( ??)
A.??????????????????????????B.??????????????????????????C.??????????????????????????D.?
2.以下由四位同学描述三角形的三种不同的说法,正确的是(?? )
A.?由三个角组成的图形叫三角形?????????????????????????????B.?由三条线段组成的图形叫三角形 C.?由三条直线组成的图形叫三角形?????????????????????????D.?由不在同一直线上的三条线段首尾顺次相接所组成的图形叫三角形
3.图中的三角形被木板遮住了一部分,这个三角形是(?? )
A.?锐角三角形?????????????????????B.?直角三角形???????????????????????C.?钝角三角形?????????????????????D.?以上都有可能
4.若三角形的两个内角的和是85°,那么这个三角形是(??? )
A.?钝角三角形????????????????????????B.?直角三角形????????????????????????C.?锐角三角形????????????????????????D.?不能确定
5.若三角形三个内角度数比为2:3:4,则这个三角形一定是( )
A.?锐角三角形????????????????????????B.?直角三角形????????????????????????C.?钝角三角形????????????????????????D.?不能确定
6.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有________对
7.如图所示,将多边形分割成三角形、图(1)中可分割出2个三角形;图(2)中可分割出3个三角形;图(3)中可分割出4个三角形;由此你能猜测出,n边形可以分割出________个三角形.
8.如图,正方形网格中每一个小正方形的边长都为1,每一个小格的顶点叫做格点.以格点为顶点分别按下列要求画三角形:
⑴在图1中,画一个三角形,使它的边长都是有理数;
⑵在图2、图3中分别画一个直角三角形,使它们的边长都是无理数,并且要求两个三角形不全等.
二、三角形三边关系(共6题)
9.有两根6cm、11cm的木棒,小明同学要想以这两根木棒做一个三角形,可以选用第三根木棒的长为(???? )
A.?3cm???????????????????????????????????B.?16cm???????????????????????????????????C.?20cm???????????????????????????????????D.?24cm
10.平行四边形一边的长是10cm,则这个平行四边形的两条对角线长可以是( ???)
A.?4cm或6cm?????????????????????B.?6cm或8cm?????????????????????C.?8cm或12cm?????????????????????D.?20cm或30cm
11.已知三角形的三边长均为偶数,其中两边长分别为2和8,则第三边长为________.
12.在△ABC中,AC=5,BC=2,且AB长为奇数.
(1)求△ABC的周长;
(2)判定△ABC的形状.
13.从1、2、3、4…、2004中任选k个数,使所选的k个数中一定可以找到能构成三角形边长的三个数(这里要求三角形三边长互不相等),试问满足条件的k的最小值是多少?
14.化简 - ,并求值。其中a与2,3分别为△ABC三边长,且a为整数。
三、内角和定理(共4题)
15.在△ABC中,已知 ∠A=3∠C=54° ,则∠B的度数是(?? )
A.?90°??????????????????????????????????????B.?94°??????????????????????????????????????C.?98°??????????????????????????????????????D.?108°
16.如图,一把直尺的边缘AB 经过一块三角板 DCB 的直角顶点B,交斜边CD 于点A,直尺的边缘EF 分别交CD、BD 于点E、F,若∠D=60°,∠ABC=20°,则∠1 的度数为(? )
A.?25°???????????????????????????????????????B.?40°???????????????????????????????????????C.?50°???????????????????????????????????????D.?80°
17.已知三角形ABC的三个内角满足关系∠B+∠C=3∠A,则此三角形(?? ?).
A.?一定有一个内角为45°?????B.?一定有一个内角为60°?????C.?一定是直角三角形?????D.?一定是钝角三角形
18.如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为________°.
四、真题演练(共7题)
19.在下列长度的三条线段中,不能组成三角形的是( ??)
A.?2 cm, 3 cm. 4cm??????????B.?3 cm, 6 cm. 6cm??????????C.?2 cm, 2 cm, 6cm??????????D.?5 cm, 6 cm. 7 cm
20.已知三角形的两边分别为1和4,第三边长为整数 ,则该三角形的周长为(? )
A.?7???????????????????????????????????????????B.?8???????????????????????????????????????????C.?9???????????????????????????????????????????D.?10
21.若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是( ??)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?8
22.已知n正整数,若一个三角形的三边长分别是n+2、n+8、3n,则满足条件的n的值有( ??)
A.?4个???????????????????????????????????????B.?5个???????????????????????????????????????C.?6个???????????????????????????????????????D.?7个
23.在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为________度.
24.如图,墙上钉着三根木条,a,b,c,量得∠1=70°,∠2=100°,那么木条a,b所在直线所夹的锐角是( ??)
A.?5°???????????????????????????????????????B.?10°???????????????????????????????????????C.?30°???????????????????????????????????????D.?70°
25.在△ABC中,若一个内角等于另两个内角的差,则(??? )
A.?必有一个内角等于30°?????????????????????????????????????????B.?必有一个内角等于45° C.?必有一个内角等于60°?????????????????????????????????????????D.?必有一个内角等于90°
答案解析部分
一、三角形的定义与分类
1. C
解:∵由不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角形,
∴C符合三角形的概念.
故答案为:C
【分析】根据三角形的定义判断即可。
2. D
解:考察三角形的概念,D为三角形的完整定义,是正确的。
故答案为:D
【分析】三角形是由三条线段顺次首尾相连,组成的一个闭合的平面图形。根据定义即可判断。
3. D
解:从图中,只能看到一个角是锐角,其它的两个角中,可以都是锐角或有一个钝角或有一个直角.
故答案为:D.
【分析】根据题意可知,三角形有一个锐角,所以可能分别是三种三角形。
4. A
解:∵ 三角形的两个内角的和是85°, ∴该三角形的第三个角的度数为: 180°-85°=95°, ∴ 这个三角形是 钝角三角形. 故答案为:A. 【分析】根据三角形角的特征分类:锐角三角形:三个角都是锐角的三角形;直角三角形:有一个角是直角的三角形;钝角三角形:有一个角是钝角的三角形;由此即可得出答案. ?
5. A
解:已知内角度数比为2:3:4,根据三角形内角和等于180°可以算出三个角分别为40°,60°,80°,所以为锐角三角形.
故答案为:A
【分析】有一个角是钝角的三角形是钝角三角形,有一个角是直角的三角形是直角三角形,三个角都是锐角的三角形是锐角三角形,由三角形的三个内角的度数之比为2:3:4及三个内角的和是180°,即可算出各个内角的度数,根据最大内角的度数即可得出结论。
6.3
解:图中以BC为公共边的”共边三角形”有△ABC,△DBC,△EBC,共3对.故答案为:3
【分析】找出图中以BC为公共边的”共边三角形”即可。
7. (n﹣1)
解: n边形可以分割出(n﹣1)个三角形.
【分析】三角形分割成了两个三角形,四边形分割成了三个三角形,以此类推,n边形分割成了(n-1)个三角形.
8. 解:
【分析】(1)掌握有理数的概念,以及形成三角形的条件,作图即可。 (2)理解无理数的定义,以及形成直角三角形的条件,按具体要求作图即可。
二、三角形三边关系
9. B
解:根据题意可得,11﹣6<第三边的长<11+6,
∴5<第三边的长<17,
则只有16cm符合.
故答案为:B.
【分析】根据三角形的三边关系即可求解.
10. D
解:A.∵对角线长为4,6, ∴2+3<10,A不符合题意; B.∵对角线长为6,8, ∴3+4<10,B不符合题意; C.∵对角线长为8,12, ∴4+6<10,C不符合题意; D.∵对角线长为20,30, ∴10+15>10,D符合题意; 故答案为:D. 【分析】根据三角形三边关系:两边之和大于第三边,依此逐一分析即可得出答案.
11. 8
解:设第三边的长x, ∴8-2<x<8+2, ∴6<x<10, ∵x为偶数, ∴a=8. 故答案为:8.
【分析】设第三边的长x,根据“三角形两边之和大于第三边,三角形的两边之差小于第三边”可得6<x<10,再根据x为偶数即可求出第三边长.
12. (1)解:由题意得:5﹣2<AB<5+2,
即:3<AB<7,
∵AB为奇数,
∴AB=5,
∴△ABC的周长为5+5+2=12 (2)解:∵AB=AC=5,
∴△ABC是等腰三角形.
【分析】(1)利用三角形三边关系定理求出AB的取值范围,再根据AB长为奇数,确定出AB的值,然后求出△ABC的周长。 (2)由(1)可知AB=AC,即可判定出△ABC的形状。
13. 解:为使k达到最大,可选加入之数等于已得数组中最大的两数之和,这样得:
1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597 ①
共16个数,对符合上述条件的任数组,a1 , a2…an显然总有ai大于等于①中的第i个数,
所以n≤16≤k﹣1,
k﹣1≥16,
解得k≥17.
故k的最小值为17.
【分析】根据三角形三边关系定理,可知为使k达到最大,可选加入之数等于已得数组中最大的两数之和,就可得到这样的数一共有16个,因此可得出n≤16≤k﹣1,解不等式,求出k的取值范围,然后求出k的最小值。
14. 解:原式= ?· ?+ ?
= + ?
= ?
=
∵a与2,3构成△ABC的三边,
∴1<a<5,且a为整数,∴a=2,3,4,
又∵a≠2且a≠3,否则分式无意义,∴a=4,
当a=4时,原式=1
【分析】先根据分式乘法的法则计算分式的乘法,再根据异分母分式相加减的法则计算,结果化为最简分式;根据三角形三边的关系可求出a的取值范围,再根据分母不能为0求出a,把a的值代入化简的式子中求值即可.
三、内角和定理
15. D
解:∵∠A=3∠C=54° ∴∠C=18° ∴∠B=180°-∠A-∠C=180°-54°-18°=108° 故答案为:D
【分析】根据已知条件求出∠C的度数,再根据三角形内角和定理求出∠B的度数。
16. C
解:∵∠CBD=90°,
∴∠ABD=90°﹣∠ABC==90°-20°=70°,
∵EF∥AB,
∴∠DFE=∠ABD=70°,
∴∠DEF=180°﹣∠D﹣∠DFE=50°,
∴∠1=∠DEF=50°,
故答案为:C.
【分析】根据角的和差算出∠ABD的度数,根据二直线平行,同位角相等得出∠DFE=∠ABD=70°,根据三角形的内角和算出∠DEF的度数,最后根据对顶角相等算出∠1的度数。
17. A
解:∵∠A+∠B+∠C=180°,
∴∠B+∠C=180°-∠A,
又∵∠B+∠C=3∠A,
∴3∠A=180°-∠A,
∴∠A=45°.
故答案为:A.
【分析】根据三角形的内角和定理得出∠B+∠C=180°-∠A,又 ∠B+∠C=3∠A 从而列出方程求出∠A的度数,即可得出答案。
18. 180°
解:∵将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,
∴∠B=∠HOG,∠A=∠DOE,∠C=∠EOF,∠1+∠2+∠HOG+∠EOF+∠DOE=360°,
∵∠HOG+∠EOF+∠DOE=∠A+∠B+∠C=180°,
∴∠1+∠2=360°?180°=180,
故答案为:180. 【分析】根据折叠的性质,可得∠B=∠HOG,∠A=∠DOE,∠C=∠EOF,利用三角形内角和定理,可得∠HOG+∠EOF+∠DOE=∠A+∠B+∠C=180°,由周角的定义,即可求出∠1+∠2的度数.
四、真题演练
19. C
解:A、2+3>4,4-2<3, 故A能组成三角形,不符合题意; B、3+6>7,7-3>6, 故B能组成三角形,不符合题意; C、2+2<6,故C不能组成三角形,符合题意; D、5+6>, 7-5<6, 故D能组成三角形,不符合题意. 故答案为:C 【分析】根据三角形两边之和大于第三边,两边之差小于第三边。两边之和用较小的两边相加和最大边比较,两边之差用最大边减最小边之差和另外一边比较。
20. C
解:设第三边为x,
根据三角形的三边关系,得:4-1<x<4+1,
即3<x<5,
∵x为整数,
∴x的值为4.
?三角形的周长为1+4+4=9.
故答案为:C.
【分析】根据三角形的三边关系可得第三边的值为4.从而得到三角形的周长为1+4+4=9.
21. C
解:∵三角形三边长分别为:a,3,5,
∴a的取值范围为:2<a<8,
∴a的所有可能取值为:3,4,5,6,7.
故答案为:C.
【分析】三角形三边的关系:两边之和大于第三边,两边之差小于第三边,由此得出a的取值范围,从而可得答案.
22. D
解:方法一:∵n是正整数
∴n=1时,三边为3,9,3构不成三角形,不符合
n=2时,三边为4,10,6构不成三角形,不符合
n=3时,三边为5,11,9可以构成三角形,符合
n=4时,三边为6,12,12可以构成三角形,符合
n=5时,三边为7,13,15可以构成三角形,符合
n=6时,三边为8,14,18可以构成三角形,符合
n=7时,三边为9,15,21可以构成三角形,符合
n=8时,三边为10,16,24可以构成三角形,符合
n=9时,三边为11,17,27可以构成三角形,符合
n=10时,三边为12,18,30不可以构成三角形,不符合
∴总共7个
方法二:当n+8最大时 ∴n=3
当3n最大时 ∴n=4,5,6,7,8,9
综上:n总共有7个 故答案为:D
【分析】方法一:分别根据n=1、2、3、4、5、6、7、8、9、10的时候,由有理数的加法及乘法运算算出三条线段的长度,再根据三角形三边关系判断这三条线段能否围成三角形,即可得出结论;方法二:分别根据n+8最大与3n最大两种情况,由三角形的任意两边之和大于第三边,任意两边之差小于第三边列出不等式组,求解得出其整数解即可。
23. 60或10
解:∵ △ABC中,∠A=50°,∠B=30°, ∴∠ACB=180°-∠A-∠B=180°-50°-30°=100° ∵ 点D在AB边上, △ACD为直角三角形 当∠ACD=90°,∠BCD=∠ACB-∠ACD=100°-90°=10°; 当∠ADC=90°时,∠ACD=90°-∠A=90°-50°=40° ∴∠BCD=∠ACB-∠ACD=100°-40°=60°; 故答案为:60或10 【分析】利用三角形内角和定理求出∠ACB的度数,再由已知点D在AB边上, △ACD为直角三角形,分两种情况讨论:当∠ACD=90°时,当∠ADC=90°时,分别求出∠BCD的度数。
24. B
解:如图,
∵∠2=∠3=100°,∠1=70°
∴a、b两直线所夹的锐角为:180°-∠1-∠3=180°-70°-100°=10°
故答案为:B
【分析】根据对顶角相等,可求出∠3的度数,再利用三角形内角和定理就可求出a、b两直线所夹的锐角的度数。
25. D
解:设△ABC的三个内角分别为A、B、C,依题可得,
A=B-C ①,
又∵A+B+C=180°②,
②-①得:
2B=180°,
∴B=90°,
∴△ABC必有一个内角等于90°.
故答案为:D.
【分析】根据题意列出等式A=B-C①,再由三角形内角和定理得A+B+C=180°②,由②-①可得B=90°,由此即可得出答案
一、三角形的定义与分类(共8题)
1.下面是小明用三根火柴组成的图形,其中符合三角形概念的是( ??)
A.??????????????????????????B.??????????????????????????C.??????????????????????????D.?
2.以下由四位同学描述三角形的三种不同的说法,正确的是(?? )
A.?由三个角组成的图形叫三角形?????????????????????????????B.?由三条线段组成的图形叫三角形 C.?由三条直线组成的图形叫三角形?????????????????????????D.?由不在同一直线上的三条线段首尾顺次相接所组成的图形叫三角形
3.图中的三角形被木板遮住了一部分,这个三角形是(?? )
A.?锐角三角形?????????????????????B.?直角三角形???????????????????????C.?钝角三角形?????????????????????D.?以上都有可能
4.若三角形的两个内角的和是85°,那么这个三角形是(??? )
A.?钝角三角形????????????????????????B.?直角三角形????????????????????????C.?锐角三角形????????????????????????D.?不能确定
5.若三角形三个内角度数比为2:3:4,则这个三角形一定是( )
A.?锐角三角形????????????????????????B.?直角三角形????????????????????????C.?钝角三角形????????????????????????D.?不能确定
6.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有________对
7.如图所示,将多边形分割成三角形、图(1)中可分割出2个三角形;图(2)中可分割出3个三角形;图(3)中可分割出4个三角形;由此你能猜测出,n边形可以分割出________个三角形.
8.如图,正方形网格中每一个小正方形的边长都为1,每一个小格的顶点叫做格点.以格点为顶点分别按下列要求画三角形:
⑴在图1中,画一个三角形,使它的边长都是有理数;
⑵在图2、图3中分别画一个直角三角形,使它们的边长都是无理数,并且要求两个三角形不全等.
二、三角形三边关系(共6题)
9.有两根6cm、11cm的木棒,小明同学要想以这两根木棒做一个三角形,可以选用第三根木棒的长为(???? )
A.?3cm???????????????????????????????????B.?16cm???????????????????????????????????C.?20cm???????????????????????????????????D.?24cm
10.平行四边形一边的长是10cm,则这个平行四边形的两条对角线长可以是( ???)
A.?4cm或6cm?????????????????????B.?6cm或8cm?????????????????????C.?8cm或12cm?????????????????????D.?20cm或30cm
11.已知三角形的三边长均为偶数,其中两边长分别为2和8,则第三边长为________.
12.在△ABC中,AC=5,BC=2,且AB长为奇数.
(1)求△ABC的周长;
(2)判定△ABC的形状.
13.从1、2、3、4…、2004中任选k个数,使所选的k个数中一定可以找到能构成三角形边长的三个数(这里要求三角形三边长互不相等),试问满足条件的k的最小值是多少?
14.化简 - ,并求值。其中a与2,3分别为△ABC三边长,且a为整数。
三、内角和定理(共4题)
15.在△ABC中,已知 ∠A=3∠C=54° ,则∠B的度数是(?? )
A.?90°??????????????????????????????????????B.?94°??????????????????????????????????????C.?98°??????????????????????????????????????D.?108°
16.如图,一把直尺的边缘AB 经过一块三角板 DCB 的直角顶点B,交斜边CD 于点A,直尺的边缘EF 分别交CD、BD 于点E、F,若∠D=60°,∠ABC=20°,则∠1 的度数为(? )
A.?25°???????????????????????????????????????B.?40°???????????????????????????????????????C.?50°???????????????????????????????????????D.?80°
17.已知三角形ABC的三个内角满足关系∠B+∠C=3∠A,则此三角形(?? ?).
A.?一定有一个内角为45°?????B.?一定有一个内角为60°?????C.?一定是直角三角形?????D.?一定是钝角三角形
18.如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为________°.
四、真题演练(共7题)
19.在下列长度的三条线段中,不能组成三角形的是( ??)
A.?2 cm, 3 cm. 4cm??????????B.?3 cm, 6 cm. 6cm??????????C.?2 cm, 2 cm, 6cm??????????D.?5 cm, 6 cm. 7 cm
20.已知三角形的两边分别为1和4,第三边长为整数 ,则该三角形的周长为(? )
A.?7???????????????????????????????????????????B.?8???????????????????????????????????????????C.?9???????????????????????????????????????????D.?10
21.若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是( ??)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?8
22.已知n正整数,若一个三角形的三边长分别是n+2、n+8、3n,则满足条件的n的值有( ??)
A.?4个???????????????????????????????????????B.?5个???????????????????????????????????????C.?6个???????????????????????????????????????D.?7个
23.在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为________度.
24.如图,墙上钉着三根木条,a,b,c,量得∠1=70°,∠2=100°,那么木条a,b所在直线所夹的锐角是( ??)
A.?5°???????????????????????????????????????B.?10°???????????????????????????????????????C.?30°???????????????????????????????????????D.?70°
25.在△ABC中,若一个内角等于另两个内角的差,则(??? )
A.?必有一个内角等于30°?????????????????????????????????????????B.?必有一个内角等于45° C.?必有一个内角等于60°?????????????????????????????????????????D.?必有一个内角等于90°
答案解析部分
一、三角形的定义与分类
1. C
解:∵由不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角形,
∴C符合三角形的概念.
故答案为:C
【分析】根据三角形的定义判断即可。
2. D
解:考察三角形的概念,D为三角形的完整定义,是正确的。
故答案为:D
【分析】三角形是由三条线段顺次首尾相连,组成的一个闭合的平面图形。根据定义即可判断。
3. D
解:从图中,只能看到一个角是锐角,其它的两个角中,可以都是锐角或有一个钝角或有一个直角.
故答案为:D.
【分析】根据题意可知,三角形有一个锐角,所以可能分别是三种三角形。
4. A
解:∵ 三角形的两个内角的和是85°, ∴该三角形的第三个角的度数为: 180°-85°=95°, ∴ 这个三角形是 钝角三角形. 故答案为:A. 【分析】根据三角形角的特征分类:锐角三角形:三个角都是锐角的三角形;直角三角形:有一个角是直角的三角形;钝角三角形:有一个角是钝角的三角形;由此即可得出答案. ?
5. A
解:已知内角度数比为2:3:4,根据三角形内角和等于180°可以算出三个角分别为40°,60°,80°,所以为锐角三角形.
故答案为:A
【分析】有一个角是钝角的三角形是钝角三角形,有一个角是直角的三角形是直角三角形,三个角都是锐角的三角形是锐角三角形,由三角形的三个内角的度数之比为2:3:4及三个内角的和是180°,即可算出各个内角的度数,根据最大内角的度数即可得出结论。
6.3
解:图中以BC为公共边的”共边三角形”有△ABC,△DBC,△EBC,共3对.故答案为:3
【分析】找出图中以BC为公共边的”共边三角形”即可。
7. (n﹣1)
解: n边形可以分割出(n﹣1)个三角形.
【分析】三角形分割成了两个三角形,四边形分割成了三个三角形,以此类推,n边形分割成了(n-1)个三角形.
8. 解:
【分析】(1)掌握有理数的概念,以及形成三角形的条件,作图即可。 (2)理解无理数的定义,以及形成直角三角形的条件,按具体要求作图即可。
二、三角形三边关系
9. B
解:根据题意可得,11﹣6<第三边的长<11+6,
∴5<第三边的长<17,
则只有16cm符合.
故答案为:B.
【分析】根据三角形的三边关系即可求解.
10. D
解:A.∵对角线长为4,6, ∴2+3<10,A不符合题意; B.∵对角线长为6,8, ∴3+4<10,B不符合题意; C.∵对角线长为8,12, ∴4+6<10,C不符合题意; D.∵对角线长为20,30, ∴10+15>10,D符合题意; 故答案为:D. 【分析】根据三角形三边关系:两边之和大于第三边,依此逐一分析即可得出答案.
11. 8
解:设第三边的长x, ∴8-2<x<8+2, ∴6<x<10, ∵x为偶数, ∴a=8. 故答案为:8.
【分析】设第三边的长x,根据“三角形两边之和大于第三边,三角形的两边之差小于第三边”可得6<x<10,再根据x为偶数即可求出第三边长.
12. (1)解:由题意得:5﹣2<AB<5+2,
即:3<AB<7,
∵AB为奇数,
∴AB=5,
∴△ABC的周长为5+5+2=12 (2)解:∵AB=AC=5,
∴△ABC是等腰三角形.
【分析】(1)利用三角形三边关系定理求出AB的取值范围,再根据AB长为奇数,确定出AB的值,然后求出△ABC的周长。 (2)由(1)可知AB=AC,即可判定出△ABC的形状。
13. 解:为使k达到最大,可选加入之数等于已得数组中最大的两数之和,这样得:
1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597 ①
共16个数,对符合上述条件的任数组,a1 , a2…an显然总有ai大于等于①中的第i个数,
所以n≤16≤k﹣1,
k﹣1≥16,
解得k≥17.
故k的最小值为17.
【分析】根据三角形三边关系定理,可知为使k达到最大,可选加入之数等于已得数组中最大的两数之和,就可得到这样的数一共有16个,因此可得出n≤16≤k﹣1,解不等式,求出k的取值范围,然后求出k的最小值。
14. 解:原式= ?· ?+ ?
= + ?
= ?
=
∵a与2,3构成△ABC的三边,
∴1<a<5,且a为整数,∴a=2,3,4,
又∵a≠2且a≠3,否则分式无意义,∴a=4,
当a=4时,原式=1
【分析】先根据分式乘法的法则计算分式的乘法,再根据异分母分式相加减的法则计算,结果化为最简分式;根据三角形三边的关系可求出a的取值范围,再根据分母不能为0求出a,把a的值代入化简的式子中求值即可.
三、内角和定理
15. D
解:∵∠A=3∠C=54° ∴∠C=18° ∴∠B=180°-∠A-∠C=180°-54°-18°=108° 故答案为:D
【分析】根据已知条件求出∠C的度数,再根据三角形内角和定理求出∠B的度数。
16. C
解:∵∠CBD=90°,
∴∠ABD=90°﹣∠ABC==90°-20°=70°,
∵EF∥AB,
∴∠DFE=∠ABD=70°,
∴∠DEF=180°﹣∠D﹣∠DFE=50°,
∴∠1=∠DEF=50°,
故答案为:C.
【分析】根据角的和差算出∠ABD的度数,根据二直线平行,同位角相等得出∠DFE=∠ABD=70°,根据三角形的内角和算出∠DEF的度数,最后根据对顶角相等算出∠1的度数。
17. A
解:∵∠A+∠B+∠C=180°,
∴∠B+∠C=180°-∠A,
又∵∠B+∠C=3∠A,
∴3∠A=180°-∠A,
∴∠A=45°.
故答案为:A.
【分析】根据三角形的内角和定理得出∠B+∠C=180°-∠A,又 ∠B+∠C=3∠A 从而列出方程求出∠A的度数,即可得出答案。
18. 180°
解:∵将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,
∴∠B=∠HOG,∠A=∠DOE,∠C=∠EOF,∠1+∠2+∠HOG+∠EOF+∠DOE=360°,
∵∠HOG+∠EOF+∠DOE=∠A+∠B+∠C=180°,
∴∠1+∠2=360°?180°=180,
故答案为:180. 【分析】根据折叠的性质,可得∠B=∠HOG,∠A=∠DOE,∠C=∠EOF,利用三角形内角和定理,可得∠HOG+∠EOF+∠DOE=∠A+∠B+∠C=180°,由周角的定义,即可求出∠1+∠2的度数.
四、真题演练
19. C
解:A、2+3>4,4-2<3, 故A能组成三角形,不符合题意; B、3+6>7,7-3>6, 故B能组成三角形,不符合题意; C、2+2<6,故C不能组成三角形,符合题意; D、5+6>, 7-5<6, 故D能组成三角形,不符合题意. 故答案为:C 【分析】根据三角形两边之和大于第三边,两边之差小于第三边。两边之和用较小的两边相加和最大边比较,两边之差用最大边减最小边之差和另外一边比较。
20. C
解:设第三边为x,
根据三角形的三边关系,得:4-1<x<4+1,
即3<x<5,
∵x为整数,
∴x的值为4.
?三角形的周长为1+4+4=9.
故答案为:C.
【分析】根据三角形的三边关系可得第三边的值为4.从而得到三角形的周长为1+4+4=9.
21. C
解:∵三角形三边长分别为:a,3,5,
∴a的取值范围为:2<a<8,
∴a的所有可能取值为:3,4,5,6,7.
故答案为:C.
【分析】三角形三边的关系:两边之和大于第三边,两边之差小于第三边,由此得出a的取值范围,从而可得答案.
22. D
解:方法一:∵n是正整数
∴n=1时,三边为3,9,3构不成三角形,不符合
n=2时,三边为4,10,6构不成三角形,不符合
n=3时,三边为5,11,9可以构成三角形,符合
n=4时,三边为6,12,12可以构成三角形,符合
n=5时,三边为7,13,15可以构成三角形,符合
n=6时,三边为8,14,18可以构成三角形,符合
n=7时,三边为9,15,21可以构成三角形,符合
n=8时,三边为10,16,24可以构成三角形,符合
n=9时,三边为11,17,27可以构成三角形,符合
n=10时,三边为12,18,30不可以构成三角形,不符合
∴总共7个
方法二:当n+8最大时 ∴n=3
当3n最大时 ∴n=4,5,6,7,8,9
综上:n总共有7个 故答案为:D
【分析】方法一:分别根据n=1、2、3、4、5、6、7、8、9、10的时候,由有理数的加法及乘法运算算出三条线段的长度,再根据三角形三边关系判断这三条线段能否围成三角形,即可得出结论;方法二:分别根据n+8最大与3n最大两种情况,由三角形的任意两边之和大于第三边,任意两边之差小于第三边列出不等式组,求解得出其整数解即可。
23. 60或10
解:∵ △ABC中,∠A=50°,∠B=30°, ∴∠ACB=180°-∠A-∠B=180°-50°-30°=100° ∵ 点D在AB边上, △ACD为直角三角形 当∠ACD=90°,∠BCD=∠ACB-∠ACD=100°-90°=10°; 当∠ADC=90°时,∠ACD=90°-∠A=90°-50°=40° ∴∠BCD=∠ACB-∠ACD=100°-40°=60°; 故答案为:60或10 【分析】利用三角形内角和定理求出∠ACB的度数,再由已知点D在AB边上, △ACD为直角三角形,分两种情况讨论:当∠ACD=90°时,当∠ADC=90°时,分别求出∠BCD的度数。
24. B
解:如图,
∵∠2=∠3=100°,∠1=70°
∴a、b两直线所夹的锐角为:180°-∠1-∠3=180°-70°-100°=10°
故答案为:B
【分析】根据对顶角相等,可求出∠3的度数,再利用三角形内角和定理就可求出a、b两直线所夹的锐角的度数。
25. D
解:设△ABC的三个内角分别为A、B、C,依题可得,
A=B-C ①,
又∵A+B+C=180°②,
②-①得:
2B=180°,
∴B=90°,
∴△ABC必有一个内角等于90°.
故答案为:D.
【分析】根据题意列出等式A=B-C①,再由三角形内角和定理得A+B+C=180°②,由②-①可得B=90°,由此即可得出答案
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
