浙教版初中数学第6章图形的初步知识单元检测(含答案)
文档属性
| 名称 | 浙教版初中数学第6章图形的初步知识单元检测(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 290.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-13 08:03:36 | ||
图片预览

文档简介
浙教版初中数学单元检测(含答案)
测试十六:第6章图形的初步知识B
1、 选择题(每小题3分,共30分)
1. 平面上有任意三个点,经过其中两点画一条直线,最多可确定直线的条数是…….( )
A.1条 B.2条
C.3条 D.无数条
2. 如果∠α=26°,那么∠α的补角等于...................( )
A.26° B.64° C.124 ° D.154°
3. 下列说法正确的是…………………………………………………( )
A.直线AB和直线BA是两条直线 B.射线AB和射线BA是两条射线
C.线段AB和线段BA是两条线段 D.直线AB和直线a不能是同一条直线
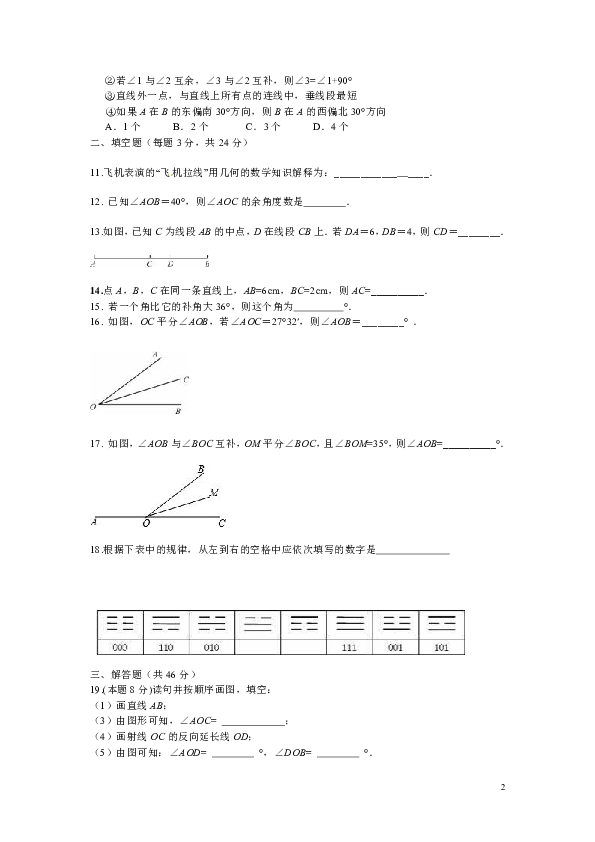
4. 下列四个图中,能用∠1、∠AOB、∠O三种方法表示同一个角的是...............( )
5. 如图所示,从A地到达B地,最短的路线是.................( )
A.A→C→E→B
B.A→F→E→B
C.A→D→E→B
D.A→C→G→E→B
6.如图,OE⊥AB于O.OC、OD分别是∠AOE、∠BOE的平分线,图中互余的角共有....( )
A.3对 B.4对 C.5对 D.6对
7.如果两个角两条边对应平行,其中一个角为34°,则另一个角度数为..............( )
A.34° B.56° C.34°或56° D.34°或146°
8.在同一平面内,如果线段MN=6cm,NP=2cm,那么M、P两点的距离是…………..( )
A.8cm B.4cm C.8cm或4cm D.无法确定
9.如图,AB、CD交于点O,∠AOE=90°,若∠AOC:∠COE=5:4,则∠AOD大小为....( )
A.120° B.130° C.140° D.150°
10.下列说法中,正确的有..............................( )
①三点三十分,时针与分针的夹角为75°
②若∠1与∠2互余,∠3与∠2互补,则∠3=∠1+90°
③直线外一点,与直线上所有点的连线中,垂线段最短
④如果A在B的东偏南30°方向,则B在A的西偏北30°方向
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共24分)
11.飞机表演的“飞机拉线”用几何的数学知识解释为:____________ ____.
12. 已知∠AOB=40°,则∠AOC的余角度数是 .
13.如图,已知C为线段AB的中点,D在线段CB上.若DA=6,DB=4,则CD=________.
14.点A,B,C在同一条直线上,AB=6cm,BC=2cm,则AC=__________.
15. 若一个角比它的补角大36°,则这个角为?? ?????°.
16. 如图,OC平分∠AOB,若∠AOC=27°32′,则∠AOB=________° .
17. 如图,∠AOB与∠BOC互补,OM平分∠BOC,且∠BOM=35°,则∠AOB=__________°.
18.根据下表中的规律,从左到右的空格中应依次填写的数字是
三、解答题(共46分)
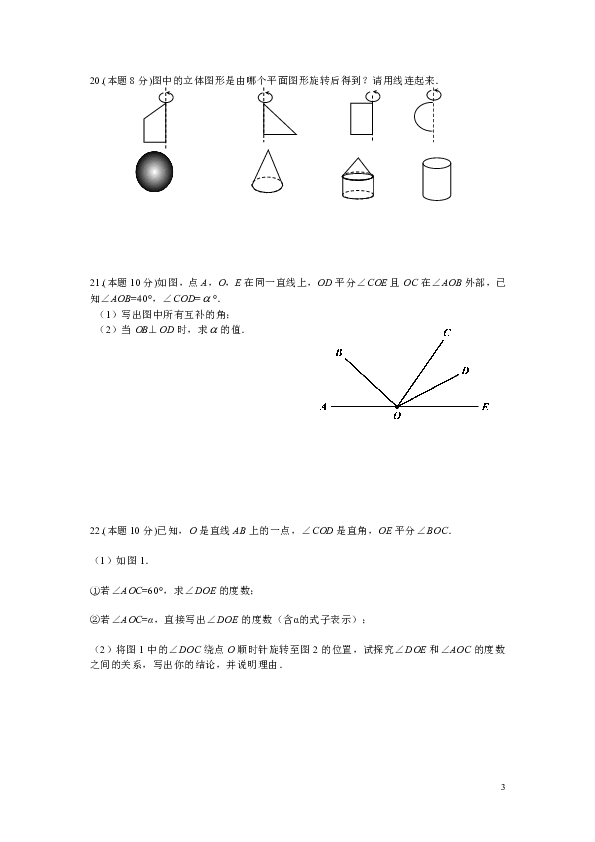
19.(本题8分)读句并按顺序画图,填空:
(1)画直线AB;
(3)由图形可知,∠AOC= ;
(4)画射线OC的反向延长线OD;
(5)由图可知:∠AOD= °,∠DOB= °.
20.(本题8分)图中的立体图形是由哪个平面图形旋转后得到?请用线连起来.
21.(本题10分)如图,点A,O,E在同一直线上,OD平分∠COE且OC在∠AOB外部,已知∠AOB=40°,∠COD=°.
(1)写出图中所有互补的角;
(2)当OB⊥OD时,求的值.
22.(本题10分)已知,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图1.
①若∠AOC=60°,求∠DOE的度数;
②若∠AOC=α,直接写出∠DOE的度数(含α的式子表示);
(2)将图1中的∠DOC绕点O顺时针旋转至图2的位置,试探究∠DOE和∠AOC的度数之间的关系,写出你的结论,并说明理由.
23. (本题10分)阅读:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|=|a﹣b|.
理解:(1)数轴上表示2和﹣3的两点之间的距离是______;
(2)数轴上表示x和﹣5的两点A和B之间的距离是????????;
(3)当代数式|x﹣1|+|x+3|取最小值时,相应的x的取值范围是???????;最小值是_____.
应用:某环形道路上顺次排列有四家快递公司:A、B、C、D,它们顺次有快递车16辆,8辆,4辆,12辆,为使各快递公司的车辆数相同,允许一些快递公司向相邻公司调出,问共有多少种调配方案,使调动的车辆数最少?并求出调出的最少车辆数.
附加题
24.为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手.
(1)一条直线把平面分成2部分;
(2)两条直线最多可把平面分成4部分;
(3)三条直线最多可把平面分成7部分…;
把上述探究的结果进行整理,列表分析:
直线条数 把平面分成部分数 写成和形式
1 2 1+1
2 4 1+1+2
3 7 1+1+2+3
4 11 1+1+2+3+4
… … …
(1)当直线条数为5时,把平面最多分成 部分,写成和的形式 ;
(2)当直线为10条时,把平面最多分成 部分;
(3)当直线为n条时,把平面最多分成 部分.(不必说明理由).
答案:
1、选择题:CDBDB DDDBD
2、填空题:
11. 点动成线
12. 50°
13. 1
14. 4或8
15. 108
16. 55°4'
17. 110°
18. 011 100
3、解答题
19. 略
20. 略
21.(1)略;
(2)此时∠DOE+∠AOB=90°,可知∠DOE=50°,即∠COD=50°
22.(1)①∵∠AOC=60°∴∠BOC=180°﹣∠AOC=120°又∵OE平分∠BOC∴∠COE=∠BOC=×120°=60°
又∵∠COD=90°∴∠DOE=∠COD﹣∠COE=30°②∠DOE=90°﹣(180﹣α)=α;
(2)∠DOE=∠AOC,理由略
23. (1)5 (2) (3),4 应用:共有5种调运方案,最少调动5辆车
24.(1)根据表中规律,当直线条数为5时,把平面最多分成16部分,1+1+2+3+4+5=16;
(2)根据表中规律,当直线为10条时,把平面最多分成56部分,为1+1+2+3+…+10=56;
(3)
第9题图
第6题图
第5题图
PAGE
1
测试十六:第6章图形的初步知识B
1、 选择题(每小题3分,共30分)
1. 平面上有任意三个点,经过其中两点画一条直线,最多可确定直线的条数是…….( )
A.1条 B.2条
C.3条 D.无数条
2. 如果∠α=26°,那么∠α的补角等于...................( )
A.26° B.64° C.124 ° D.154°
3. 下列说法正确的是…………………………………………………( )
A.直线AB和直线BA是两条直线 B.射线AB和射线BA是两条射线
C.线段AB和线段BA是两条线段 D.直线AB和直线a不能是同一条直线
4. 下列四个图中,能用∠1、∠AOB、∠O三种方法表示同一个角的是...............( )
5. 如图所示,从A地到达B地,最短的路线是.................( )
A.A→C→E→B
B.A→F→E→B
C.A→D→E→B
D.A→C→G→E→B
6.如图,OE⊥AB于O.OC、OD分别是∠AOE、∠BOE的平分线,图中互余的角共有....( )
A.3对 B.4对 C.5对 D.6对
7.如果两个角两条边对应平行,其中一个角为34°,则另一个角度数为..............( )
A.34° B.56° C.34°或56° D.34°或146°
8.在同一平面内,如果线段MN=6cm,NP=2cm,那么M、P两点的距离是…………..( )
A.8cm B.4cm C.8cm或4cm D.无法确定
9.如图,AB、CD交于点O,∠AOE=90°,若∠AOC:∠COE=5:4,则∠AOD大小为....( )
A.120° B.130° C.140° D.150°
10.下列说法中,正确的有..............................( )
①三点三十分,时针与分针的夹角为75°
②若∠1与∠2互余,∠3与∠2互补,则∠3=∠1+90°
③直线外一点,与直线上所有点的连线中,垂线段最短
④如果A在B的东偏南30°方向,则B在A的西偏北30°方向
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共24分)
11.飞机表演的“飞机拉线”用几何的数学知识解释为:____________ ____.
12. 已知∠AOB=40°,则∠AOC的余角度数是 .
13.如图,已知C为线段AB的中点,D在线段CB上.若DA=6,DB=4,则CD=________.
14.点A,B,C在同一条直线上,AB=6cm,BC=2cm,则AC=__________.
15. 若一个角比它的补角大36°,则这个角为?? ?????°.
16. 如图,OC平分∠AOB,若∠AOC=27°32′,则∠AOB=________° .
17. 如图,∠AOB与∠BOC互补,OM平分∠BOC,且∠BOM=35°,则∠AOB=__________°.
18.根据下表中的规律,从左到右的空格中应依次填写的数字是
三、解答题(共46分)
19.(本题8分)读句并按顺序画图,填空:
(1)画直线AB;
(3)由图形可知,∠AOC= ;
(4)画射线OC的反向延长线OD;
(5)由图可知:∠AOD= °,∠DOB= °.
20.(本题8分)图中的立体图形是由哪个平面图形旋转后得到?请用线连起来.
21.(本题10分)如图,点A,O,E在同一直线上,OD平分∠COE且OC在∠AOB外部,已知∠AOB=40°,∠COD=°.
(1)写出图中所有互补的角;
(2)当OB⊥OD时,求的值.
22.(本题10分)已知,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图1.
①若∠AOC=60°,求∠DOE的度数;
②若∠AOC=α,直接写出∠DOE的度数(含α的式子表示);
(2)将图1中的∠DOC绕点O顺时针旋转至图2的位置,试探究∠DOE和∠AOC的度数之间的关系,写出你的结论,并说明理由.
23. (本题10分)阅读:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|=|a﹣b|.
理解:(1)数轴上表示2和﹣3的两点之间的距离是______;
(2)数轴上表示x和﹣5的两点A和B之间的距离是????????;
(3)当代数式|x﹣1|+|x+3|取最小值时,相应的x的取值范围是???????;最小值是_____.
应用:某环形道路上顺次排列有四家快递公司:A、B、C、D,它们顺次有快递车16辆,8辆,4辆,12辆,为使各快递公司的车辆数相同,允许一些快递公司向相邻公司调出,问共有多少种调配方案,使调动的车辆数最少?并求出调出的最少车辆数.
附加题
24.为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手.
(1)一条直线把平面分成2部分;
(2)两条直线最多可把平面分成4部分;
(3)三条直线最多可把平面分成7部分…;
把上述探究的结果进行整理,列表分析:
直线条数 把平面分成部分数 写成和形式
1 2 1+1
2 4 1+1+2
3 7 1+1+2+3
4 11 1+1+2+3+4
… … …
(1)当直线条数为5时,把平面最多分成 部分,写成和的形式 ;
(2)当直线为10条时,把平面最多分成 部分;
(3)当直线为n条时,把平面最多分成 部分.(不必说明理由).
答案:
1、选择题:CDBDB DDDBD
2、填空题:
11. 点动成线
12. 50°
13. 1
14. 4或8
15. 108
16. 55°4'
17. 110°
18. 011 100
3、解答题
19. 略
20. 略
21.(1)略;
(2)此时∠DOE+∠AOB=90°,可知∠DOE=50°,即∠COD=50°
22.(1)①∵∠AOC=60°∴∠BOC=180°﹣∠AOC=120°又∵OE平分∠BOC∴∠COE=∠BOC=×120°=60°
又∵∠COD=90°∴∠DOE=∠COD﹣∠COE=30°②∠DOE=90°﹣(180﹣α)=α;
(2)∠DOE=∠AOC,理由略
23. (1)5 (2) (3),4 应用:共有5种调运方案,最少调动5辆车
24.(1)根据表中规律,当直线条数为5时,把平面最多分成16部分,1+1+2+3+4+5=16;
(2)根据表中规律,当直线为10条时,把平面最多分成56部分,为1+1+2+3+…+10=56;
(3)
第9题图
第6题图
第5题图
PAGE
1
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
