4.6 整式的加减(1)(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 4.6 整式的加减(1)(知识清单+经典例题+夯实基础+提优特训+中考链接) |

|
|
| 格式 | zip | ||
| 文件大小 | 259.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-12 00:00:00 | ||
图片预览



文档简介
浙江版2019-2020学年度七年级数学上册第4章代数式
4.6 整式的加减(1)
【知识清单】
1.去括号法则:括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变;括号前是“”,把括号和它前面的“”号去掉,括号里各项都改变符号.
2.整式加减的步骤:先去括号,再合并同类项.
3.关于整式加减的简单应用:如求图形的面积等.
【经典例题】
例题1、去括号: (a+b1)结果正确的是( )
A. a+b1 B. a+b+1 C. ab+1 D. a+b+1
【考点】去括号与添括号.
【分析】根据去括号的方法作答即可.
【解答】
(a+b1)=ab+1.
故选C.
【点评】本题考查去括号的方法:去括号时,运用乘法的分配律,先把括号前的数字与括号里各项相乘,再运用括号前是“+”,去括号后,括号里的各项都不改变符号;括号前是“”,去括号后,括号里的各项都改变符号.
例题2、一辆公交车上原来有(8a6b)人,途经A站下去一半,又上来若干人,这时车上共有乘客(11a7b)人,(1)问上车的乘客是多少人?(2)当a=3,b=2时,上车的乘客是多少人?
【考点】列代数式;代数式求值,合并同类项.?
【分析】(1)上车的乘客人数=现在车上共有人数原有的一半的人数;
(2)把a=3,b=2代入(1)得到的式子.
【解答】解:(1)由题意可得,
(11a7b)
=11a7b(4a3b)
=11a7b4a+3b
=7a4b,
即上车的乘客是(7a4b)人,
(2)当a=4,b=3时,7a4b=7×44×3=16(人).
【点评】解决问题的关键是读懂题意,找到所求的量的等量关系.
【夯实基础】
1、[2x3(yz)]去括号后应得( )
A.2x+3yz B.2x3y+3z C.2x3yz D.2x+3y3z
2、计算4(2x3y)+5(3x4y)的结果是( )
A.7xy B.7x+8y C.7x8y D.7x8y
3、下列各式与5x(2y+3z)相等的是( )
A.5x+(2y+3z) B.5x+(2y3z)
C.5x+(3y+4z) D.2x+(2y3z)
4、若ab=3,bc=5,则(ac)23(ac)3等于( )
A.7 B.7 C.5 D.5
5、若a+b=7,ab=9,则(5a6b3ab)(3a8b+ab)= .
6、已知a2ab=11,b2ab=8,则代数式3a23b2的值为 .
7、去括号:[(3a)+(3b)]= .
8、化简(1) 2x3y4(2xy);
(2)4 (2a23b2) 2(4a23b2);
(3)3a2b3(2a2b3ab2)+4(ab23a2b);
(4) 15a32(5ab2)+3(4ab5a3).
9、先化简,再求值
(1) a23(aa2)12(a+a2)2,其中a=2
(2)(xy)34(xy)2+3(xy)+6(xy)3+(xy)27(xy)35,其中xy=
【提优特训】
10、下列各组式子中,互为相反数的有( )
①x2y与x2y;②x+2y与x2y;③x+2y与2yx;④x+2y与x2y.
A.①②④ B.②④ C.①③ D.③④
11、若A和B都是五次多项式,则A+B一定是( )
A. 10次多项式 B. 次数不高于五次的多项式或单项式
C. 五次多项式 D. 次数不低于五次的多项式或单项式
12、下列去括号,错误的有( )个
① x2+(3x2)=x2+3x2;② 2a2(2a3)=2a22a3;③ m3(n2)=m3n6,
④ a5(bc)=a5b+5c
A. 0 B. 1 C. 2 D. 3
13、当x=2时,代数式a(x1)2+b(x1)+2的值为5,则(a+b2)(2ab)的值为( )
A. 1 B. 1 C. 2 D. 2
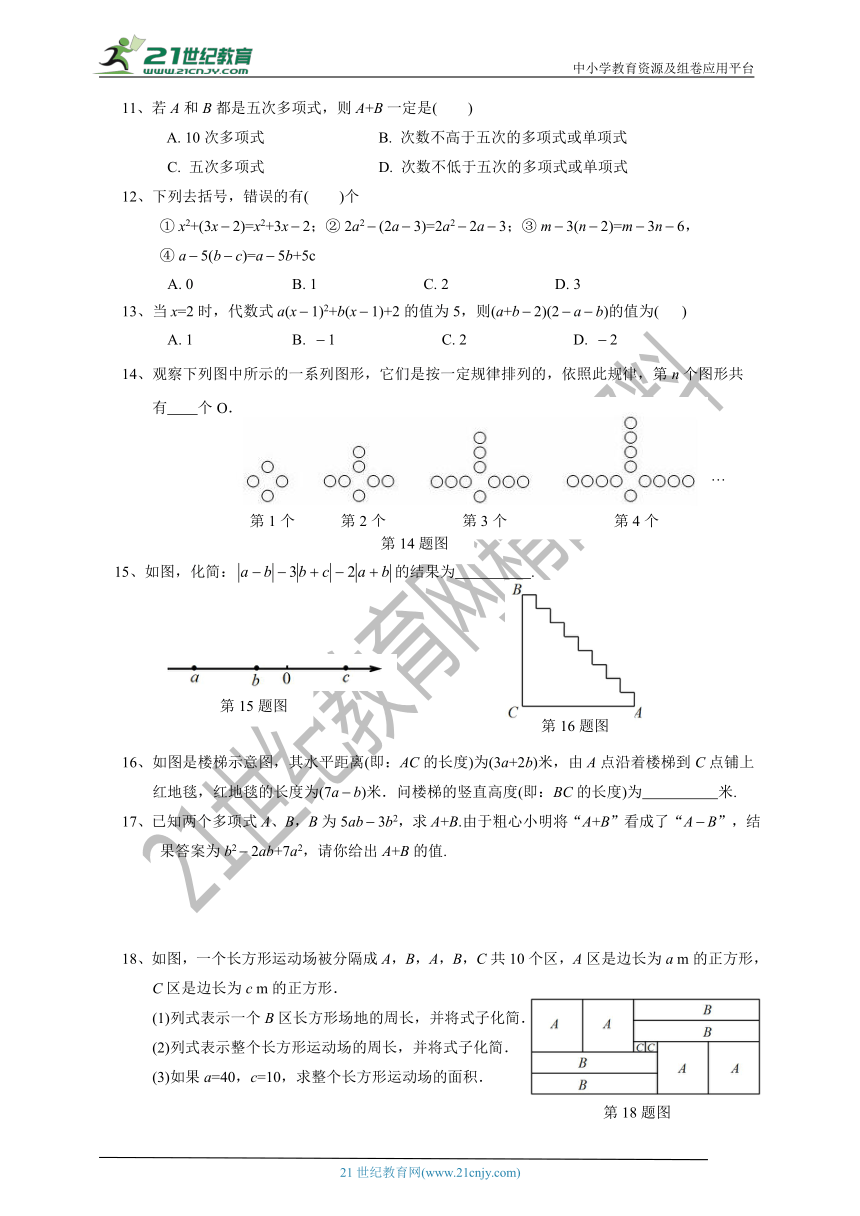
14、观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第n个图形共
有 个O.
15、如图,化简:的结果为 .
16、如图是楼梯示意图,其水平距离(即:AC的长度)为(3a+2b)米,由A点沿着楼梯到C点铺上
红地毯,红地毯的长度为(7ab)米.问楼梯的竖直高度(即:BC的长度)为 米.
17、已知两个多项式A、B,B为5ab3b2,求A+B.由于粗心小明将“A+B”看成了“AB”,结
果答案为b22ab+7a2,请你给出A+B的值.
18、如图,一个长方形运动场被分隔成A,B,A,B,C共10个区,A区是边长为a m的正方形,
C区是边长为c m的正方形.
(1)列式表示一个B区长方形场地的周长,并将式子化简.
(2)列式表示整个长方形运动场的周长,并将式子化简.
(3)如果a=40,c=10,求整个长方形运动场的面积.
19、某城市自来水费实行阶梯收费,收费标准如下表:
月用水量
不超过12吨的部分
超过12吨不超
过20吨的部分
超过20吨的部分
收费标准(元/吨)
a
a+1
4
(1)某用户七月份用水32吨,用含a的代数式表示该用户七月份所交的水费;
(2)若a=1.8元时,求该用户七月份应交的水费多少元?
20、有这样一道题:计算(5x36x2y+3xy2)+( 2x33xy2+y3)(3x37x2yy3)的值,其中x=,
y=1,小明把x=错抄成x=,但他的计算结果也是正确的,请你帮他找出原因.
21、某同学做一道代数题,求代数式10x9 +9x8 +8x7+…+3x2+2x+1,当x=1时,该代数式的值?该同学由于将式中某一项前的“+”号看成“-”号,求得代数式的值为7,那么这位同学看错了几次项前的符号?
【中考链接】
22、(2018?台湾)已知a=(),b=(),c=,判断
下列叙述何者正确?( )
A.a=c,b=c B.a=c,b≠c C.a≠c,b=c D.a≠c,b≠c
23、(2018?宜昌)1261年,我国南宋数学家杨辉用图中的三角形解释二项和的乘方规律,
比欧洲的相同发现要早三百多年,我们把这个三角形称为“杨辉三角”,请观察图中
的数字排列规律,则a,b,c的值分别为( )
A.a=1,b=6,c=15 B.a=6,b=15,c=20
C.a=15,b=20,c=15 D.a=20,b=15,c=6
24、(2018?烟台)如图所示,下列图形都是由相同的玫瑰花按照一定的规律摆成的,按此规律摆下去,第n个图形中有120朵玫瑰花,则n的值为( )
A.28 B.29 C.30 D.31
25、(2018?随州)我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10…)和“正方形数”(如1,4,9,16…),在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则m+n的值为( )
A.33
B.301
C.386
D.571
参考答案
1、D 2、C 3、B 4、A 5、22 6、9 7、a+b或ba 10、B 11、B 12、C
13、B 14、3n+1 15、a3c 16、4a3b 22、B 22、B 23、C 24、C
8、化简(1) 2x3y4(2xy);
解:原式=2x3y8x+4y
=(28)x+(3+4)y
=10x+y;
(2)4 (2a23b2) 2(4a23b2);
解:原式=8a212b28a2+6b2
=(88)a2+(12+6)b2
=6b2;
(3)3a2b3(2a2b3ab2)+4(ab23a2b);
解:原式=3a2b 6a2b+9ab2+4ab212a2b
=(3612)a2b+(9+4)ab2
=15a2b+13ab2;
(4) 15a32(5ab2)+3(4ab5a3).
解:原式= 15a310ab+4+12ab15a3
=(1515)a3+(10+12)ab+4
=2ab+4.
9、先化简,再求值
(1) a23(aa2)12(a+a2)2,其中a=2
解:原式=a23a+4a2+2+10a3a22
=(+43)a2+(3+10)a+(22)
=a2+7a
当a=2时,
原式=a2+7a= =×(2)2+7×(2)
=214=12;
(2)(xy)34(xy)2+3(xy)+6(xy)3+(xy)27(xy)35,其中xy=
原式=(1+67)(xy)3+(4+1)(xy)2+3(xy)5
=3(xy)2+3(xy)5
当xy=时,
原式=3(xy)2+3(xy) 5
=3×()2+3×()-5
=+15=.
17、已知两个多项式A、B,B为5ab3b2,求A+B.由于粗心小明将“A+B”看成了“AB”,结
果答案为b22ab+7a2,请你给出A+B的值.
解∵AB= b22ab+7a2,B=5ab3b2,
∴A= b22ab+7a2+5ab3b2
=7a2+(52)ab+(13)b2
=7a2+3ab2b2,
∴A+B=7a2+3ab2b2+5ab3b2
=7a2+(3+5)ab+(23)b2
=7a2+8ab5b2.
18、如图,一个长方形运动场被分隔成A,B,A,B,C共10个区,A区是边长为a m的正方形,
C区是边长为c m的正方形.
(1)列式表示一个B区长方形场地的周长,并将式子化简.
(2)列式表示整个长方形运动场的周长,并将式子化简.
(3)如果a=40,c=10,求整个长方形运动场的面积.
解:(1)2[(2a+2c)+]=4a+4c+a-c)=(5a+3c)(m).
(2)2[(a+a+a+a+c+c)+(a+ac)]=2(6a+c)=(12a+2c)(m).
(3)当a=22,c=4时,
长=4a+2c=96(m),宽=2ac=40(m),
所以运动场的面积=96×40=3840(m2).
19、某城市自来水费实行阶梯收费,收费标准如下表:
月用水量
不超过12吨的部分
超过12吨不超
过20吨的部分
超过20吨的部分
收费标准(元/吨)
a
a+1
4
(1)某用户七月份用水32吨,用含a的代数式表示该用户十月份所交的水费
(2)若a=1.8元时,求该用户十月份应交的水费
解:(1)12a+8(a+1)+(3220)×4=12a+8a+8+48=(20a+56)(元)
(2)若a=1.8元时, 该用户十月份应交的水费为:
20a+56=20×1.8+56=92(元).
20、有这样一道题:计算(5x36x2y+3xy2)+( 2x33xy2+y3)(3x37x2yy3)的值,其中x=,
y=1,小明把x=错抄成x=,但他的计算结果也是正确的,请你帮他找出原因.
解:(5x36x2y+3xy2)+(2x33xy2+y3)(3x37x2yy3)
=5x36x2y+3xy22x33xy2+y33x3+7x2y+y3
=(523)x3+(6+7)x2y+(33)xy2+(1+1)y3
= x2y+2y3,
∵合并的结果中的一项含x2的项,另一项不含x.
∴不论x=或x=,x2的结果都是,
∴不影响最后的结果.
21、某同学做一道代数题,求代数式10x9 +9x8 +8x7+…+3x2+2x+1,当x=-1时,该代数式的值?该
同学由于将式中某一项前的“+”号看成“-”号,求得代数式的值为7,那么这位同学看错
了几次项前的符号?
解:当x=1时,10×(1)9 +9×(1)8 +8×(1)7+…+3×(1)2 +2×(1)+1
=10+98+76+54+32+1=5,
现在答案为7,多了12
∴x=1时
7=正确的原式+12=(10x9+9x8+8x7+7x6+6x5+5x4+4x3+3x2+2x+1)+12
=(10x9+9x8+8x7+7x6+6x5+5x4+4x3+3x2+2x+1)12x5
=10x9+9x8+8x7+7x66x5+5x4+4x3+3x2+2x+1.
所以是5次项的符号改了.
4.6 整式的加减(1)
【知识清单】
1.去括号法则:括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变;括号前是“”,把括号和它前面的“”号去掉,括号里各项都改变符号.
2.整式加减的步骤:先去括号,再合并同类项.
3.关于整式加减的简单应用:如求图形的面积等.
【经典例题】
例题1、去括号: (a+b1)结果正确的是( )
A. a+b1 B. a+b+1 C. ab+1 D. a+b+1
【考点】去括号与添括号.
【分析】根据去括号的方法作答即可.
【解答】
(a+b1)=ab+1.
故选C.
【点评】本题考查去括号的方法:去括号时,运用乘法的分配律,先把括号前的数字与括号里各项相乘,再运用括号前是“+”,去括号后,括号里的各项都不改变符号;括号前是“”,去括号后,括号里的各项都改变符号.
例题2、一辆公交车上原来有(8a6b)人,途经A站下去一半,又上来若干人,这时车上共有乘客(11a7b)人,(1)问上车的乘客是多少人?(2)当a=3,b=2时,上车的乘客是多少人?
【考点】列代数式;代数式求值,合并同类项.?
【分析】(1)上车的乘客人数=现在车上共有人数原有的一半的人数;
(2)把a=3,b=2代入(1)得到的式子.
【解答】解:(1)由题意可得,
(11a7b)
=11a7b(4a3b)
=11a7b4a+3b
=7a4b,
即上车的乘客是(7a4b)人,
(2)当a=4,b=3时,7a4b=7×44×3=16(人).
【点评】解决问题的关键是读懂题意,找到所求的量的等量关系.
【夯实基础】
1、[2x3(yz)]去括号后应得( )
A.2x+3yz B.2x3y+3z C.2x3yz D.2x+3y3z
2、计算4(2x3y)+5(3x4y)的结果是( )
A.7xy B.7x+8y C.7x8y D.7x8y
3、下列各式与5x(2y+3z)相等的是( )
A.5x+(2y+3z) B.5x+(2y3z)
C.5x+(3y+4z) D.2x+(2y3z)
4、若ab=3,bc=5,则(ac)23(ac)3等于( )
A.7 B.7 C.5 D.5
5、若a+b=7,ab=9,则(5a6b3ab)(3a8b+ab)= .
6、已知a2ab=11,b2ab=8,则代数式3a23b2的值为 .
7、去括号:[(3a)+(3b)]= .
8、化简(1) 2x3y4(2xy);
(2)4 (2a23b2) 2(4a23b2);
(3)3a2b3(2a2b3ab2)+4(ab23a2b);
(4) 15a32(5ab2)+3(4ab5a3).
9、先化简,再求值
(1) a23(aa2)12(a+a2)2,其中a=2
(2)(xy)34(xy)2+3(xy)+6(xy)3+(xy)27(xy)35,其中xy=
【提优特训】
10、下列各组式子中,互为相反数的有( )
①x2y与x2y;②x+2y与x2y;③x+2y与2yx;④x+2y与x2y.
A.①②④ B.②④ C.①③ D.③④
11、若A和B都是五次多项式,则A+B一定是( )
A. 10次多项式 B. 次数不高于五次的多项式或单项式
C. 五次多项式 D. 次数不低于五次的多项式或单项式
12、下列去括号,错误的有( )个
① x2+(3x2)=x2+3x2;② 2a2(2a3)=2a22a3;③ m3(n2)=m3n6,
④ a5(bc)=a5b+5c
A. 0 B. 1 C. 2 D. 3
13、当x=2时,代数式a(x1)2+b(x1)+2的值为5,则(a+b2)(2ab)的值为( )
A. 1 B. 1 C. 2 D. 2
14、观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第n个图形共
有 个O.
15、如图,化简:的结果为 .
16、如图是楼梯示意图,其水平距离(即:AC的长度)为(3a+2b)米,由A点沿着楼梯到C点铺上
红地毯,红地毯的长度为(7ab)米.问楼梯的竖直高度(即:BC的长度)为 米.
17、已知两个多项式A、B,B为5ab3b2,求A+B.由于粗心小明将“A+B”看成了“AB”,结
果答案为b22ab+7a2,请你给出A+B的值.
18、如图,一个长方形运动场被分隔成A,B,A,B,C共10个区,A区是边长为a m的正方形,
C区是边长为c m的正方形.
(1)列式表示一个B区长方形场地的周长,并将式子化简.
(2)列式表示整个长方形运动场的周长,并将式子化简.
(3)如果a=40,c=10,求整个长方形运动场的面积.
19、某城市自来水费实行阶梯收费,收费标准如下表:
月用水量
不超过12吨的部分
超过12吨不超
过20吨的部分
超过20吨的部分
收费标准(元/吨)
a
a+1
4
(1)某用户七月份用水32吨,用含a的代数式表示该用户七月份所交的水费;
(2)若a=1.8元时,求该用户七月份应交的水费多少元?
20、有这样一道题:计算(5x36x2y+3xy2)+( 2x33xy2+y3)(3x37x2yy3)的值,其中x=,
y=1,小明把x=错抄成x=,但他的计算结果也是正确的,请你帮他找出原因.
21、某同学做一道代数题,求代数式10x9 +9x8 +8x7+…+3x2+2x+1,当x=1时,该代数式的值?该同学由于将式中某一项前的“+”号看成“-”号,求得代数式的值为7,那么这位同学看错了几次项前的符号?
【中考链接】
22、(2018?台湾)已知a=(),b=(),c=,判断
下列叙述何者正确?( )
A.a=c,b=c B.a=c,b≠c C.a≠c,b=c D.a≠c,b≠c
23、(2018?宜昌)1261年,我国南宋数学家杨辉用图中的三角形解释二项和的乘方规律,
比欧洲的相同发现要早三百多年,我们把这个三角形称为“杨辉三角”,请观察图中
的数字排列规律,则a,b,c的值分别为( )
A.a=1,b=6,c=15 B.a=6,b=15,c=20
C.a=15,b=20,c=15 D.a=20,b=15,c=6
24、(2018?烟台)如图所示,下列图形都是由相同的玫瑰花按照一定的规律摆成的,按此规律摆下去,第n个图形中有120朵玫瑰花,则n的值为( )
A.28 B.29 C.30 D.31
25、(2018?随州)我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10…)和“正方形数”(如1,4,9,16…),在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则m+n的值为( )
A.33
B.301
C.386
D.571
参考答案
1、D 2、C 3、B 4、A 5、22 6、9 7、a+b或ba 10、B 11、B 12、C
13、B 14、3n+1 15、a3c 16、4a3b 22、B 22、B 23、C 24、C
8、化简(1) 2x3y4(2xy);
解:原式=2x3y8x+4y
=(28)x+(3+4)y
=10x+y;
(2)4 (2a23b2) 2(4a23b2);
解:原式=8a212b28a2+6b2
=(88)a2+(12+6)b2
=6b2;
(3)3a2b3(2a2b3ab2)+4(ab23a2b);
解:原式=3a2b 6a2b+9ab2+4ab212a2b
=(3612)a2b+(9+4)ab2
=15a2b+13ab2;
(4) 15a32(5ab2)+3(4ab5a3).
解:原式= 15a310ab+4+12ab15a3
=(1515)a3+(10+12)ab+4
=2ab+4.
9、先化简,再求值
(1) a23(aa2)12(a+a2)2,其中a=2
解:原式=a23a+4a2+2+10a3a22
=(+43)a2+(3+10)a+(22)
=a2+7a
当a=2时,
原式=a2+7a= =×(2)2+7×(2)
=214=12;
(2)(xy)34(xy)2+3(xy)+6(xy)3+(xy)27(xy)35,其中xy=
原式=(1+67)(xy)3+(4+1)(xy)2+3(xy)5
=3(xy)2+3(xy)5
当xy=时,
原式=3(xy)2+3(xy) 5
=3×()2+3×()-5
=+15=.
17、已知两个多项式A、B,B为5ab3b2,求A+B.由于粗心小明将“A+B”看成了“AB”,结
果答案为b22ab+7a2,请你给出A+B的值.
解∵AB= b22ab+7a2,B=5ab3b2,
∴A= b22ab+7a2+5ab3b2
=7a2+(52)ab+(13)b2
=7a2+3ab2b2,
∴A+B=7a2+3ab2b2+5ab3b2
=7a2+(3+5)ab+(23)b2
=7a2+8ab5b2.
18、如图,一个长方形运动场被分隔成A,B,A,B,C共10个区,A区是边长为a m的正方形,
C区是边长为c m的正方形.
(1)列式表示一个B区长方形场地的周长,并将式子化简.
(2)列式表示整个长方形运动场的周长,并将式子化简.
(3)如果a=40,c=10,求整个长方形运动场的面积.
解:(1)2[(2a+2c)+]=4a+4c+a-c)=(5a+3c)(m).
(2)2[(a+a+a+a+c+c)+(a+ac)]=2(6a+c)=(12a+2c)(m).
(3)当a=22,c=4时,
长=4a+2c=96(m),宽=2ac=40(m),
所以运动场的面积=96×40=3840(m2).
19、某城市自来水费实行阶梯收费,收费标准如下表:
月用水量
不超过12吨的部分
超过12吨不超
过20吨的部分
超过20吨的部分
收费标准(元/吨)
a
a+1
4
(1)某用户七月份用水32吨,用含a的代数式表示该用户十月份所交的水费
(2)若a=1.8元时,求该用户十月份应交的水费
解:(1)12a+8(a+1)+(3220)×4=12a+8a+8+48=(20a+56)(元)
(2)若a=1.8元时, 该用户十月份应交的水费为:
20a+56=20×1.8+56=92(元).
20、有这样一道题:计算(5x36x2y+3xy2)+( 2x33xy2+y3)(3x37x2yy3)的值,其中x=,
y=1,小明把x=错抄成x=,但他的计算结果也是正确的,请你帮他找出原因.
解:(5x36x2y+3xy2)+(2x33xy2+y3)(3x37x2yy3)
=5x36x2y+3xy22x33xy2+y33x3+7x2y+y3
=(523)x3+(6+7)x2y+(33)xy2+(1+1)y3
= x2y+2y3,
∵合并的结果中的一项含x2的项,另一项不含x.
∴不论x=或x=,x2的结果都是,
∴不影响最后的结果.
21、某同学做一道代数题,求代数式10x9 +9x8 +8x7+…+3x2+2x+1,当x=-1时,该代数式的值?该
同学由于将式中某一项前的“+”号看成“-”号,求得代数式的值为7,那么这位同学看错
了几次项前的符号?
解:当x=1时,10×(1)9 +9×(1)8 +8×(1)7+…+3×(1)2 +2×(1)+1
=10+98+76+54+32+1=5,
现在答案为7,多了12
∴x=1时
7=正确的原式+12=(10x9+9x8+8x7+7x6+6x5+5x4+4x3+3x2+2x+1)+12
=(10x9+9x8+8x7+7x6+6x5+5x4+4x3+3x2+2x+1)12x5
=10x9+9x8+8x7+7x66x5+5x4+4x3+3x2+2x+1.
所以是5次项的符号改了.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
