3.6圆内接四边形~3.7正多边形~3.8弧长及扇形的面积 同步检测卷 有答案
文档属性
| 名称 | 3.6圆内接四边形~3.7正多边形~3.8弧长及扇形的面积 同步检测卷 有答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-13 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙教版初中九年级同步检测卷(含答案)
卷九:圆的基本性质(3.6~3.8)
一、选择题(每小题3分,共30分)
1. 如图,A,B,C,D在⊙O上,若∠D=70°,则∠B的度数是…… ( )
A.70° B.90° C.110° D.130°
2. 平行四边形的四个顶点在同一圆上,则该平行四边形一定是(???? )
A.正方形???? B.菱形? C.矩形 ?D.以上都不是
3.一个多边形的每一个外角都等于45°,则这个多边形的边数是…… ( )
A.6 B.8 C.10 D.12
4. 如图,CA和CE是正六形ABCDEF的对角线,则∠ACE的大小是…… ( )
A.50° B.60° C.70° D.80°
5. 已知⊙O的内接正六边形周长为36cm,则这个圆的半径是(???? )
A.3cm? B.6cm? C.9cm? D.12cm
6. 弦心距为4 ,弦长为8 的弦所对的劣弧长是……( )
A. B. C. D.
7. 如图,AB为半圆O的直径,C是半圆上一点,且∠COA=60°,设扇形AOC、△COB、弓形BmC的面积为S1、S2、S3,则它们之间的关系是( )
A.S1<S2<S3????????B.S2<S1<S3????????C.S1<S3<S2???????D.S3<S2<S1
8. 如图,一把折扇展开后是一个扇形,其中圆心角为120°,OB=2,AB=3,则折扇纸面部分的面积为( )
A.1?? ??? B. C.7?? ????D.
9. 如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中阴影部分的面积为( )
A.? B.???? C. D.
10. 如图,在扇形OAB中,∠AOB=90°,点C是上的一个动点(不与A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E.若DE=1,则扇形OAB的面积为( )
A. B. ?C. ?D.
二、填空题(每小题3分,共18分)
11.半径为6cm的半圆的弧长为 cm.
12. 扇形的弧长是cm,其圆心角是90°,则扇形的扇形的面积是?????? cm2.
13.已知弧长公式是,若已知弧长l和半径r,则求圆心角的公式是 .
14.AB是一个正边形的一条边,O是正多边形外接圆的圆心,若⊿AOB的一个内角等于
70°,则= .
15. 如图,以正三角形ABC的AB边为直径画⊙O,分别交AC,BC于点D, E, AB=6cm,
则的长是 .
16.如图,半圆O的直径AB=2,弦CD∥AB,∠COD=90°,则图中阴影部分的面积为?????.
?
三、解答题(共52分)
17.(本题6分)一个扇形的圆心角为100°,弧长为,求这个扇形的面积.
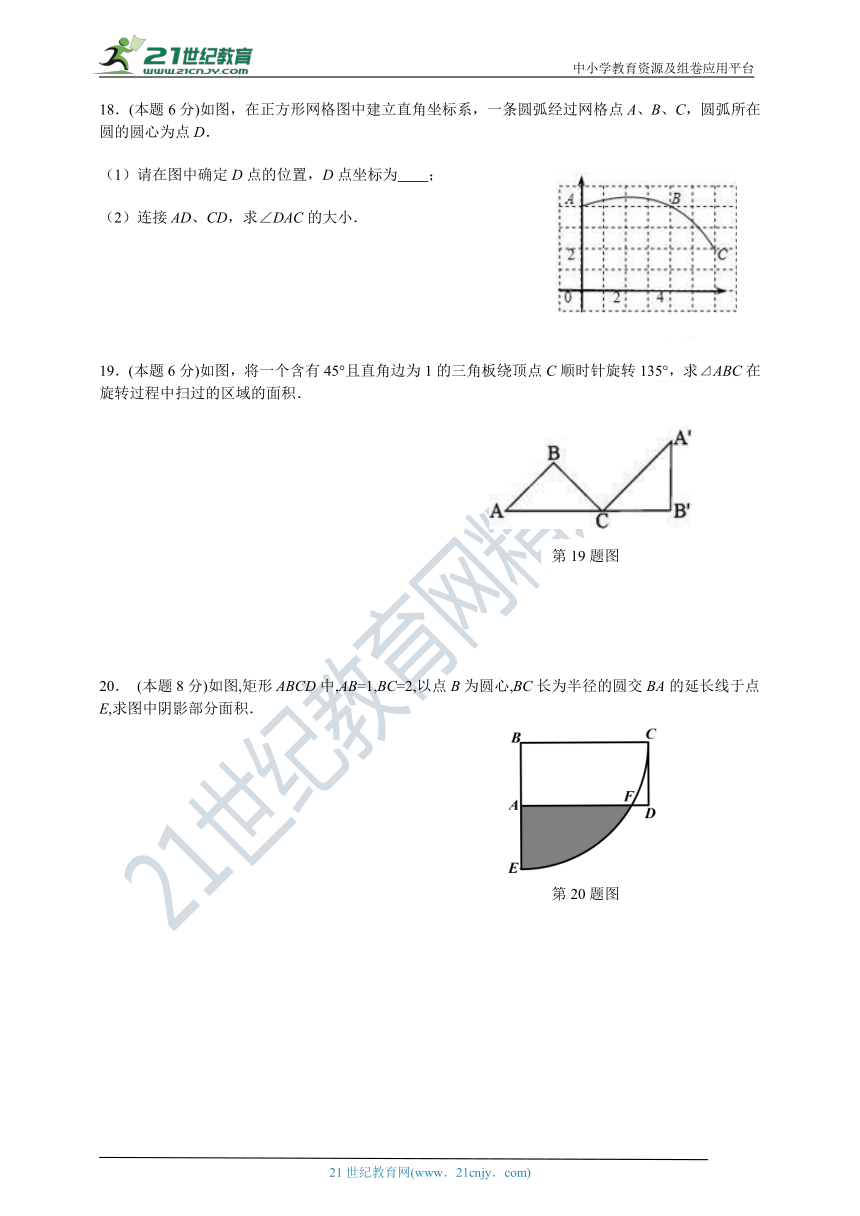
18.(本题6分)如图,在正方形网格图中建立直角坐标系,一条圆弧经过网格点A、B、C,圆弧所在圆的圆心为点D.
(1)请在图中确定D点的位置,D点坐标为 ;
(2)连接AD、CD,求∠DAC的大小.
19.(本题6分)如图,将一个含有45°且直角边为1的三角板绕顶点C顺时针旋转135°,求⊿ABC在旋转过程中扫过的区域的面积.
20. (本题8分)如图,矩形ABCD中,AB=1,BC=2,以点B为圆心,BC长为半径的圆交BA的延长线于点E,求图中阴影部分面积.
21.(本题8分)在⊿ABC中,AB=4cm,∠A=30°,∠B=45°,以点A为圆心,AC长为半径画弧分别与AB和BC交于点E和点F.
(1)求的长;
(2)求CF的长.
22.(本题8分) 已知:如图,为的直径,交于点,交 于点.
(1)求的大小;
(2)求证:.
23.(本题10分) 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.
(1)求证:CB∥PD;
(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.
附加题(本题10分)如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A、与大圆相交于点B.AC⊥OA与大圆相交于点D,且CO平分∠ACB.
(1)求证:点O到直线BC的距离等于OA;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由;
(3)若AB=8cm,BC=10cm,求大圆与小圆围成的圆环的面积.(结果保留π)
参考答案
一、 选择题
1 2 3 4 5 6 7 8 9 10
C C B B B A B D C A
二、填空题:
11.
12.
13.
14.9
15.
16.
三、解答题
17.
18. (1)图略;D(2,0)
(2)作CE⊥x轴,垂足为E.∵△AOD≌△DEC,∴∠OAD=∠CDE,又∵∠OAD+∠ADO=90°,∴∠CDE+∠ADO=90°,∴扇形DAC的圆心角为90°;
19.
20.
21.(1) ;(2)过A作AH⊥BC于H,则BH=FH=,而BC=
∴CF=
22.(1) ;(2)连接AD,则AD⊥BC. ∵AB=AC∴BD=CD
23. (1)∵∠PBC=∠D,∠PBC=∠C,∴∠C=∠D,∴CB∥PD;
(2)AB是⊙O的直径,弦CD⊥AB于点E,∴,
∵∠PBC=∠C=22.5°,∴∠BOC=∠BOD=2∠C=45°,∴∠AOC=180°﹣∠BOC=135°,
∴劣弧AC的长为:
24.(1)过O作OH⊥BC,利用全等证明;
(2)BC=AC+AD
(3)由勾股定理得AC=6,∴CH=6,BH=4,由(2)知AD=4.而圆环的面积为= =
第4题图
第1题图
第9题图
第10题图
第15题图
第16题图
第19题图
第20题图
第21题图
第22题图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
