第3章 圆的基本性质 单元测试（B卷）

中小学教育资源及组卷应用平台


浙教版初中九年级同步检测卷（含答案）
卷十一：圆的基本性质(综合B)
一、选择题(每小题3分,共30分)
1. 如图，点A是⊙O上一点，若∠OBC=55°，则∠A=（　　）
A．35°? B．45°? C．55°? D．70°
2. 已知90°的圆心角所对弧长为5π cm，则这条弧所在圆的
半径为……（ ）
A.7cm B 8cm C. 9cm D. 10cm
3．如图，如果AB为⊙O的直径，弦CD⊥AB，垂足为E，那么下列结论中，错误的是（ ）
A．CE=DE B． C．∠BAC=∠BAD D．OE=BE
4. ⊙O的半径为5，圆心O的到点P的距离为4，则点P与⊙O的位置关系是（　）
A．点P在⊙O内? B．点P的⊙O上??C．点P在⊙O外 D．点P在⊙O上或⊙O外





5．如图，⊙O的直径CD垂直弦AB于点E，且CE=2，DE=8，则AB的长为（　）
A．2???? B．4????? C．6???? D．8
6. 如图，AB是⊙O的弦，半径OA=2，∠AOB=120°，则弦AB的长是（　　）
A． ?B． ?C． ?? D．
7．如图，已知A,B,C在⊙O上，且∠A+∠B=130°,则圆周角∠ACB的度数是…( )
A.80° B.100° C.120° D.130°
8. 已知⊙O的半径为2cm,弦AB长为cm,则这条弦的中点到弦所对劣弧的中点的距离为…… ( )
A．1 B．2 C．3 D．4
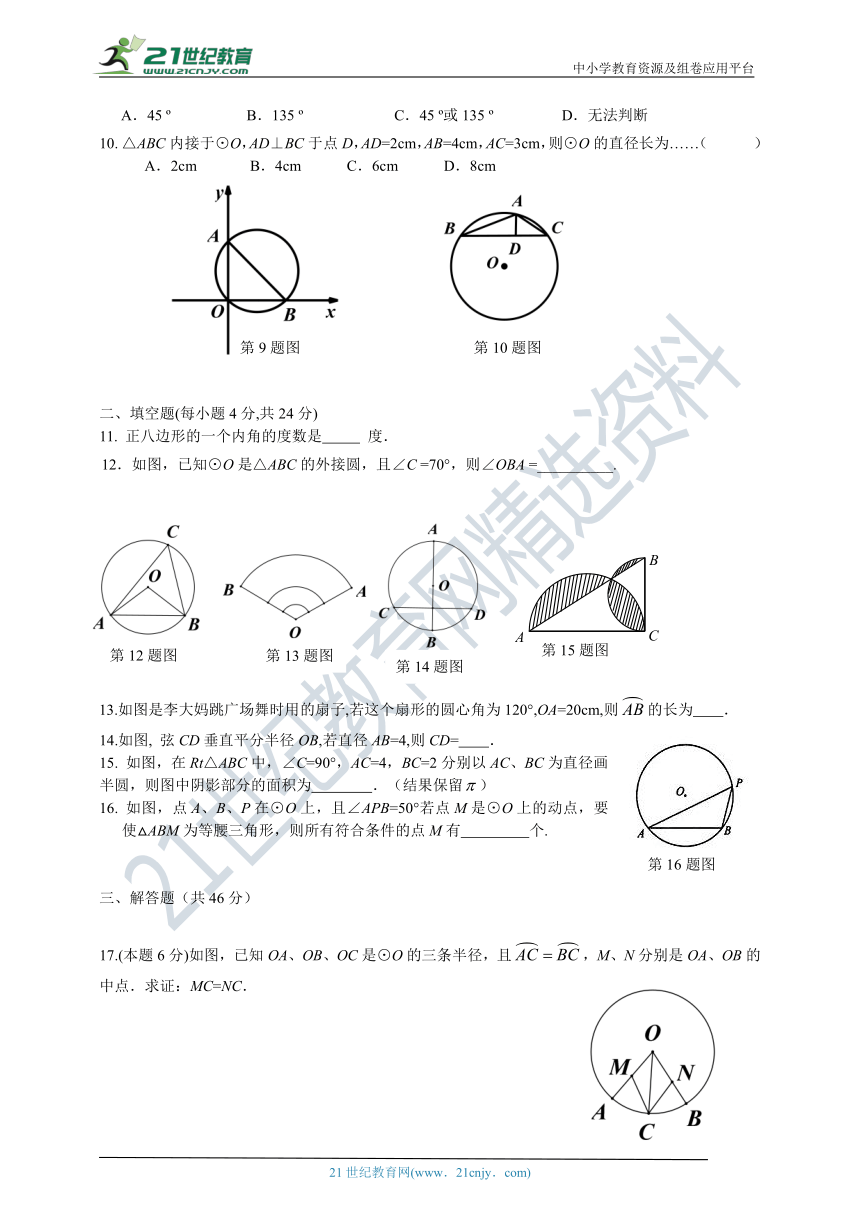
9．如图，在平面直角坐标系中，P是经过O（0，0）、A（0，2）、B（2，0）的圆上的一个动点（P与A、B不重合），则∠OPB的度数是…… ( )
A．45 ? B．135 ? C．45 ?或135 ? D．无法判断
10. △ABC内接于⊙O，AD⊥BC于点D，AD=2cm，AB=4cm，AC=3cm，则⊙O的直径长为……（ ）
A．2cm B．4cm C．6cm D．8cm










二、填空题(每小题4分,共24分)
11. 正八边形的一个内角的度数是　 度．
12．如图，已知⊙O是△ABC的外接圆，且∠C =70°，则∠OBA =__________.









13.如图是李大妈跳广场舞时用的扇子,若这个扇形的圆心角为120°,OA=20cm,则的长为　　．
14.如图, 弦CD垂直平分半径OB,若直径AB=4,则CD=　　．
15. 如图，在Rt△ABC中，∠C=90°，AC=4，BC=2分别以AC、BC为直径画半圆，则图中阴影部分的面积为 ．（结果保留）
16. 如图，点A、B、P在⊙O上，且∠APB=50°若点M是⊙O上的动点，要使△ABM为等腰三角形，则所有符合条件的点M有 个.


三、解答题（共46分）
17.(本题6分)如图，已知OA、OB、OC是⊙O的三条半径，且，M、N分别是OA、OB的中点．求证：MC=NC．

　

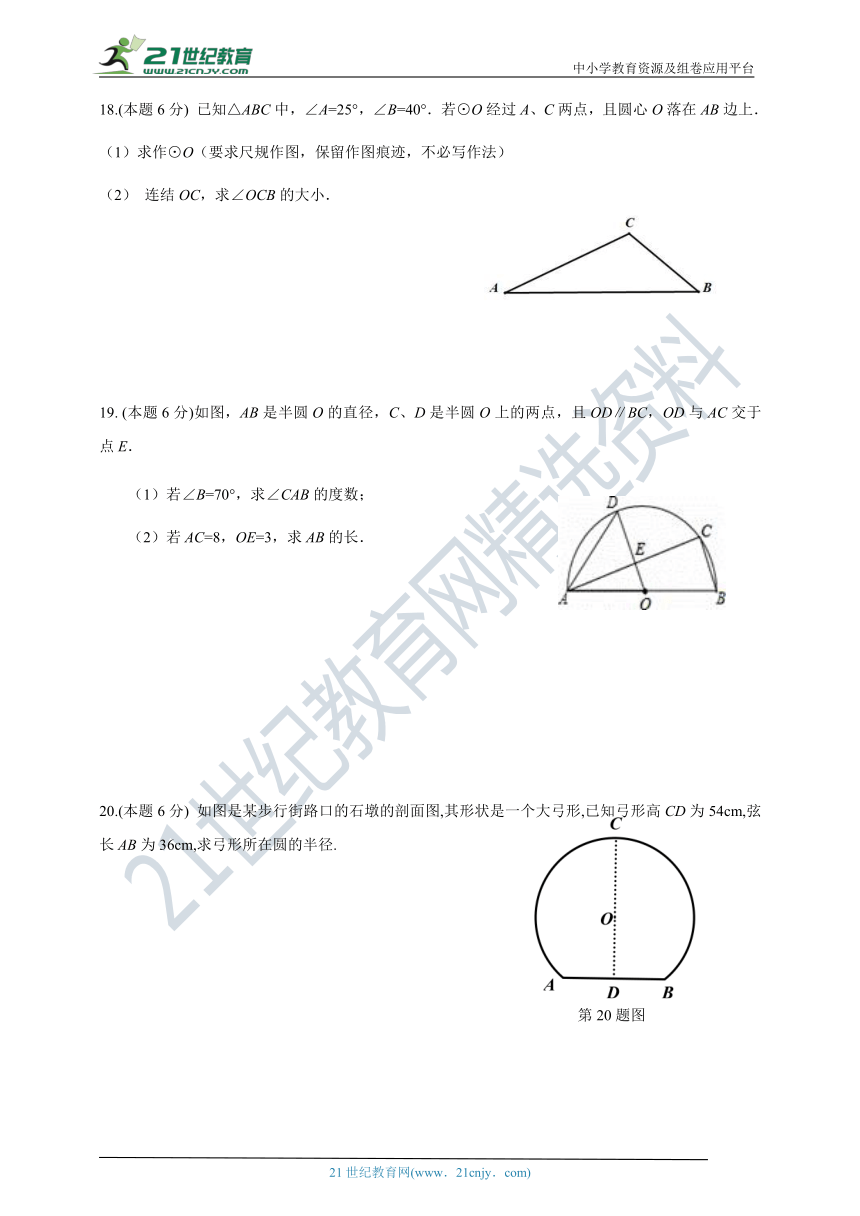
18.(本题6分) 已知△ABC中，∠A=25°，∠B=40°． (?http:?/??/?www.21cnjy.com?/??)若⊙O经过A、C两点，且圆心O落在AB边上．
（1）求作⊙O（要求尺规作图，保留作图痕迹，不必写作法）
（2） 连结OC，求∠OCB的大小．





19. (本题6分)如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E．
（1）若∠B=70°，求∠CAB的度数；
（2）若AC=8，OE=3，求AB的长．










20.(本题6分) 如图是某步行街路口的石墩的剖面图,其形状是一个大弓形,已知弓形高CD为54cm,弦长AB为36cm,求弓形所在圆的半径.












22.(本题6分)如图，已知AB是⊙O的直径，弦CD⊥AB，垂足为E，∠AOC=60°，OC=2．
(1) 求OE和CD的长；
(2) 求图中阴影部分的面积．









22.(本题8分) 如图，四边形ABCD内接于⊙O，点E在对角线AC上，EC=BC=DC．
（1）若∠CBD=39°，求∠BAD的度数；
（2）求证：∠1=∠2．



　




23.(本题8分)如图，公路MN和村路PQ在P处交汇，且∠QPN=30°，点A处有一所中学，AP=160m．假设拖拉机行驶时，周围100m以内会受到噪声的影响，那么拖拉机在公路MN上沿PN方向行驶时，学校是否会受到噪声影响？请说明理由；如果受影响，已知拖拉机的速度为18km/h时，那么学校受影响的时间为多少秒？










附加题：
如图，以点P（﹣1，0）为圆心的圆，交x轴于B、C两点（B在C的左侧），交y轴于A、D两点（A在D的下方），AD=2，将△ABC绕点P旋转180°，得到△MCB．
（1）求B、C两点的坐标；
（2）请在图中画出线段MB、MC，并判断四边形ACMB的形状（不必证明），求出点M的坐标；
（3）动直线l从与BM重合的位置开始绕点B顺时针旋转，到与BC重合时停止，设直线l与CM交点为E，点Q为BE的中点，过点E作EG⊥BC于G，连接MQ、QG．请问在旋转过程中∠MQG的大小是否变化？若不变，求出∠MQG的度数；若变化，请说明理由．























参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
A D D A D B C A C C
二、填空题
11.135° 12.20° 13.
14. 15. 16.4
三、解答题
17. ∵，∴∠AOC=∠BOC，又∵M、N分别是OA、OB的中点∴OM=ON，∴△MOC≌△NOC（SAS），∴MC=NC．

18.500m
19.
20.30cm
21.（1）；（2）此时∠A＝60°，AC＝，∴
22. （1）由BC=DC，得∠CBD=∠CDB=39°，∵∠BAC=∠CDB=39°，∠CAD=∠CBD=39°，∴∠BAD=∠BAC+∠CAD=39°+39°=78°；
（2）∵EC=BC，∴∠CEB=∠CBE，而∠CEB=∠2+∠BAE，∠CBE=∠1+∠CBD，∴∠2+∠BAE=∠1+∠CBD，∵∠BAE=∠BDC=∠CBD，∴∠1=∠2．
23. （1）过点A作AH⊥MN于H，则AH＝80，会受到影响；
（2）以点A为圆心，100为半径作圆，与MN交于E，F两点，利用垂径定理得：EF＝120（m）
18km/h＝5m/s，（s）
24. （1）连接PA，可得OA=，OP=1，BP=CP=2．∴B（﹣3，0），C（1，0）．
（2）连接AP，延长AP交⊙P于点M，连接MB、MC可得四边形ACMB是矩形．
过点M作MH⊥BC，垂足为H，∴△MHP≌△AOP．∴点M的坐标为（﹣2，）．
（3）在旋转过程中∠MQG的大小不变．可得QM=QE=QB=QG．
∴∠OCA=60°，∠MBC=∠BCA=60°，∠MQG=120°．∴在旋转过程中∠MQG的大小不变，始终等于120°．






第5题图

第7题图

第6题图

第3题图

第9题图

第10题图

第14题图

第12题图

C

A

B

第15题图

第13题图

第16题图

第20题图

第22题图



第23题图



21世纪教育网 www．21cnjy．com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www．21cnjy．com)