浙教版数学八上1.1认识三角形 同步练习(2课时打包,含答案)
文档属性
| 名称 | 浙教版数学八上1.1认识三角形 同步练习(2课时打包,含答案) | 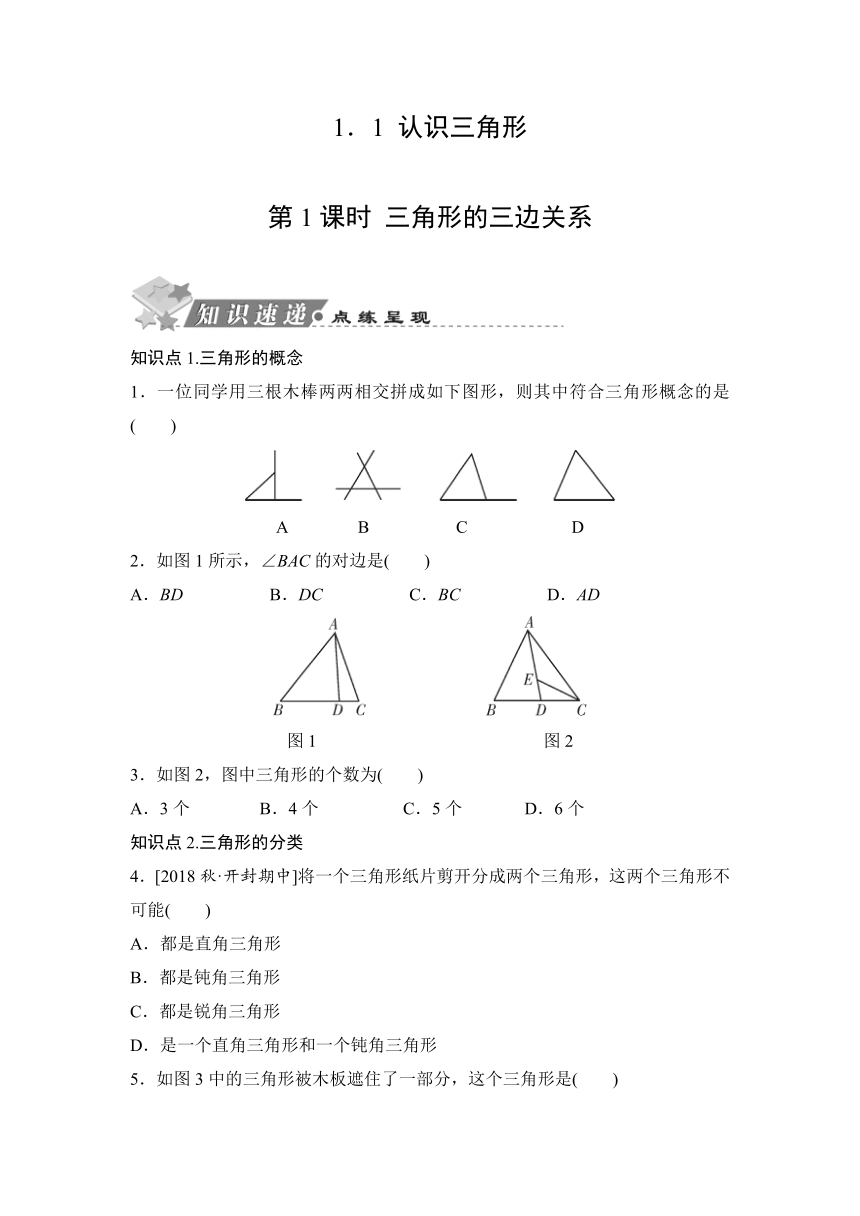 | |
| 格式 | zip | ||
| 文件大小 | 265.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 13:16:48 | ||
图片预览




文档简介
1.1 认识三角形
第1课时 三角形的三边关系
知识点1.三角形的概念
1.一位同学用三根木棒两两相交拼成如下图形,则其中符合三角形概念的是( )
A B C D
2.如图1所示,∠BAC的对边是( )
A.BD B.DC C.BC D.AD
图1 图2
3.如图2,图中三角形的个数为( )
A.3个 B.4个 C.5个 D.6个
知识点2.三角形的分类
4.[2018秋·开封期中]将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是直角三角形
B.都是钝角三角形
C.都是锐角三角形
D.是一个直角三角形和一个钝角三角形
5.如图3中的三角形被木板遮住了一部分,这个三角形是( )
图3
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
知识点3.三角形的三边关系
6.下列长度的三根小木棒能构成三角形的是( )
A.2 cm,3 cm,5 cm
B.7 cm,4 cm,2 cm
C.3 cm,4 cm,8 cm
D.3 cm,3 cm,4 cm
7.若一个三角形的两边长分别为3和7,则第三边长可能是( )
A.6 B.3 C.2 D.11
8.用一条长为25 cm的细绳围成一个等腰三角形,若其中有一边的长为7 cm,则该等腰三角形的腰长为__ __.
9.如图4是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板另外一个角∠C的度数为( )
图4
A.30° B.40°
C.50° D.60°
10.在△ABC中,
(1)若∠A=30°,∠B=80°,则∠C=____;
(2)若∠A=50°,∠B=∠C,则∠C=____;
(3)若∠A∶∠B∶∠C=1∶3∶5,则∠A=____,∠B=____,∠C=____.
【易错点】求与等腰三角形有关的边长时,没有指明已知边是底还是腰时,需要分类讨论,注意利用三边关系检验.
11.用一条长为20 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边长为5 cm的等腰三角形吗?如果能,请求出它的另两边的长度.
第2课时 三角形的高线、中线与角平分线
知识点1.三角形的高线
1.过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A B
C D
2.如果一个三角形两边上的高线的交点在三角形的内部,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.任意三角形
3.[2018秋·黄石港区校级期中]如图1,在△ABC中,AD,AE分别是△ABC的高线和角平分线,若∠B=40°,∠EAD=15°,求∠C的度数.
图1
知识点2.三角形的中线
4.如图2,D,E分别是△ABC的边AC,BC的中点,那么下列说法中不正确的是( )
图2
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=DC,BE=EC
D.AD=EC,DC=BE
5.三角形一边上的中线把原三角形一定分成两个( )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
6.如图3,已知在△ABC中,CF,BE分别是AB,AC边上的中线,若AE=2,AF=3,且△ABC的周长为15,求BC的长.
图3
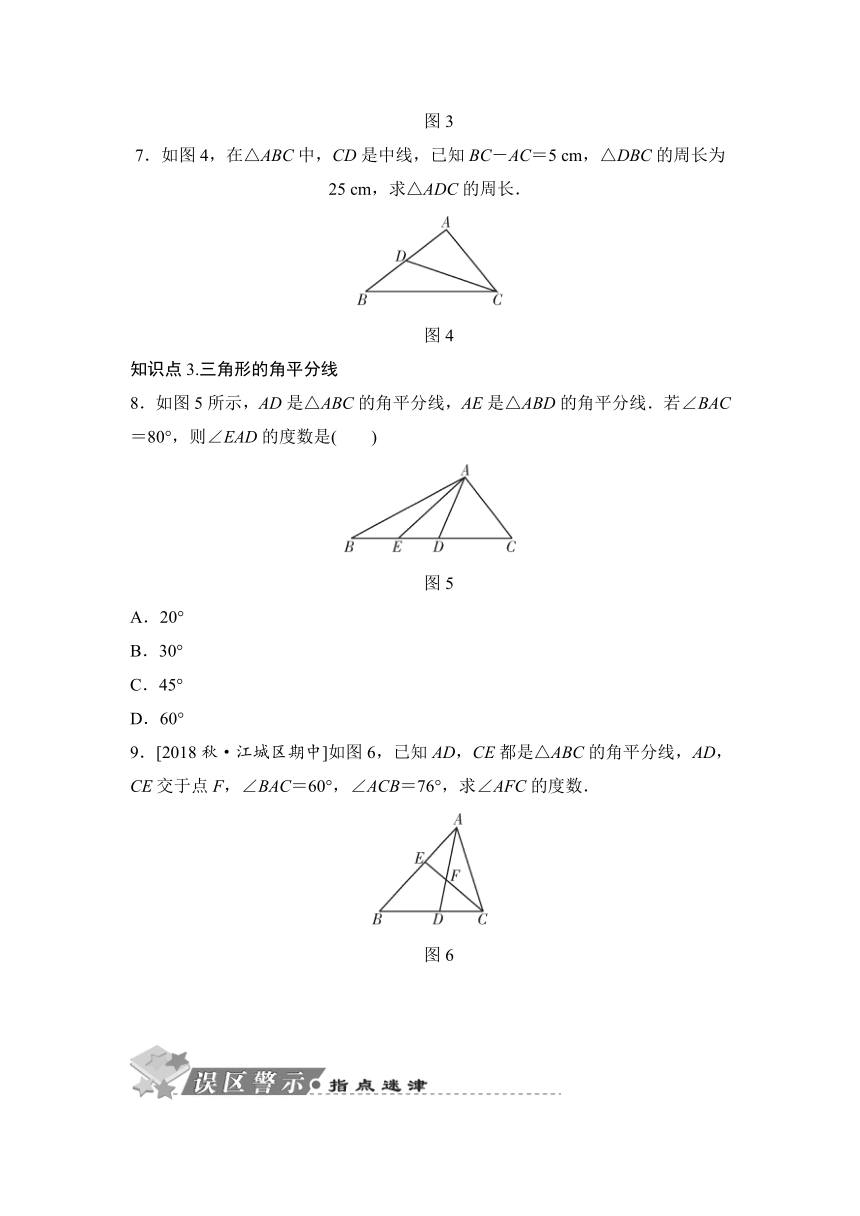
7.如图4,在△ABC中,CD是中线,已知BC-AC=5 cm,△DBC的周长为25 cm,求△ADC的周长.
图4
知识点3.三角形的角平分线
8.如图5所示,AD是△ABC的角平分线,AE是△ABD的角平分线.若∠BAC=80°,则∠EAD的度数是( )
图5
A.20°
B.30°
C.45°
D.60°
9.[2018秋·江城区期中]如图6,已知AD,CE都是△ABC的角平分线,AD,CE交于点F,∠BAC=60°,∠ACB=76°,求∠AFC的度数.
图6
【易错点】不能正确理解三角形的高线、中线和角平分线的概念.
10.三角形中:①中线、角平分线、高线都是线段;②三条高必交于一点;③三条角平分线必交于一点;④三条高必在三角形内.其中正确的是( )
A.①② B.①③
C.②④ D.③④
综合练习
一、选择题(本题共有6小题,每小题5分,共30分)
1.[湖州校级期中]已知一个三角形的两边长分别为3和4,则第三边的长不可能的是( )
A.2 B.3 C.4 D.1
2.[杭州萧山区期末]下列各组数不可能是一个三角形的边长的是( )
A.5,5,5 B.5,7,7
C.5,12,13 D.5,7,12
3.[嘉兴秀洲区校级期中]一个三角形的两个内角分别为60°和20°,则这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.不能确定
4.[杭州西湖区校级期中]下列各图中,正确画出AC边上的高的是( )
5.[宁波江北区校级期末]已知等腰三角形(有两条边相等)的其中两边长分别为4,9,则这个等腰三角形的周长是( )
A.13 B.17
C.22 D.17或22
【
6.[湖州校级期中]如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的有( )
(第6题图)
①AD是△ABE的角平分线;
②BE是△ABD的边AD上的中线;
③CH是△ACD的边AD上的高;
④AH是△ACF的角平分线和高.
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共有6小题,每小题5分,共30分)
7.[温州鹿城区校级期中]△ABC中,已知∠A=80°,∠B=60°,则∠C=____.
8.[台州校级期中]如图,一副分别含有30°和45°的两个直角三角板,拼成如图图形,其中∠C=90°,∠B=45°,∠E=30°.则∠BFD的度数是____.
(第8题图) (第9题图)
9.[嘉兴秀洲区校级期中]如图,已知BE和CF是△ABC的两条高,∠ABC=48°,∠ACB=76°,则∠FDE=____.
10.如图,∠ACB=90°,∠CAB=∠CBA,BE⊥CE,∠ABE=15°,则∠ACE=____.
(第10题图) (第11题图)
11.[杭州西湖区校级期中]如图,∠1=2∠2,∠3=2∠4,∠5=2∠6,E,C,F在同一条直线上,若∠A=63°,则∠E=____,∠F=___.
12.[余姚期中]如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC的面积是16 cm2,则阴影部分的面积等于____cm2.
(第12题图)
三、解答题(本题共有4小题,共40分)
13.(10分)[绍兴柯桥区校级期中]如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
(第13题图)
14.(10分)[青羊区校级期中]已知a,b,c分别是△ABC的三边,化简:|a+b+c|+|a+c-b|-|c-a-b|.
15.(10分)[绍兴柯桥校级期中]平面上有n个点(n≥3),任意三点不在同一直线上,过任意三点作三角形,一共能作多少个不同的三角形?
(1)分析:当有3个点时,可作____个三角形;
当有4个点时,可作____个三角形;
当有5个点时,可作____个三角形…
(2)请归纳点的个数n和可以作出三角形的个数Sn的关系.
16.(10分)[杭州西湖区校级期中]“综合与实践”学习活动准备制作一组三角形.记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于0且小于4的整数个单位长度,用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,3,3)表示边长分别为2,3,3个单位长度的一个三角形,请列举出所有满足条件的三角形.
答案
知识点1.三角形的概念
1.一位同学用三根木棒两两相交拼成如下图形,则其中符合三角形概念的是( D )
A B C D
2.如图1所示,∠BAC的对边是( C )
A.BD B.DC C.BC D.AD
图1 图2
3.如图2,图中三角形的个数为( C )
A.3个 B.4个 C.5个 D.6个
【解析】 图中的三角形为△ABD,△ACE,△DCE,△ACD和△ABC,共5个三角形.
知识点2.三角形的分类
4.[2018秋·开封期中]将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( C )
A.都是直角三角形
B.都是钝角三角形
C.都是锐角三角形
D.是一个直角三角形和一个钝角三角形
【解析】 如答图①,沿三角形一边上的高剪开即可得到两个直角三角形;
① ② ③
第4题答图
如答图②,钝角三角形沿虚线剪开即可得到两个钝角三角形;
如答图③,直角三角形沿虚线剪开即可得到一个直角三角形和一个钝角三角形.
∵剪开的边上的两个角互补,故这两个三角形不可能都是锐角三角形.
5.如图3中的三角形被木板遮住了一部分,这个三角形是( D )
图3
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
知识点3.三角形的三边关系
6.下列长度的三根小木棒能构成三角形的是( D )
A.2 cm,3 cm,5 cm
B.7 cm,4 cm,2 cm
C.3 cm,4 cm,8 cm
D.3 cm,3 cm,4 cm
7.若一个三角形的两边长分别为3和7,则第三边长可能是( A )
A.6 B.3 C.2 D.11
8.用一条长为25 cm的细绳围成一个等腰三角形,若其中有一边的长为7 cm,则该等腰三角形的腰长为__7 cm或9 cm__.
【解析】 7 cm是腰长时,底边为25-7×2=11,
∵7+7>11,∴7 cm,7 cm,11 cm能组成三角形;
7 cm是底边时,腰长为×(25-7)=9 cm,
7 cm,9 cm,9 cm能够组成三角形.
综上所述,它的腰长为7 cm或9 cm.
知识点4.三角形的内角和定理
9.如图4是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板另外一个角∠C的度数为( B )
图4
A.30° B.40°
C.50° D.60°
10.在△ABC中,
(1)若∠A=30°,∠B=80°,则∠C=__70°__;
(2)若∠A=50°,∠B=∠C,则∠C=__65°__;
(3)若∠A∶∠B∶∠C=1∶3∶5,则∠A=__20°__,∠B=__60°__,∠C=__100°__.
【易错点】求与等腰三角形有关的边长时,没有指明已知边是底还是腰时,需要分类讨论,注意利用三边关系检验.
11.用一条长为20 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边长为5 cm的等腰三角形吗?如果能,请求出它的另两边的长度.
解:(1)设底边长为x cm,则腰长为2x cm,则
2x+2x+x=20,解得x=4,
∴2x=8,∴各边长为8 cm,8 cm,4 cm;
(2)①当5 cm为底时,腰长=7.5 cm;
②当5 cm为腰时,底边=10 cm,∵5+5=10,故不能构成三角形,舍去.
∴能构成有一边长为5 cm的等腰三角形,另两边长为7.5 cm,7.5 cm.
第2课时 三角形的高线、中线与角平分线
知识点1.三角形的高线
1.过△ABC的顶点A,作BC边上的高,以下作法正确的是( A )
A B
C D
2.如果一个三角形两边上的高线的交点在三角形的内部,那么这个三角形是( A )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.任意三角形
3.[2018秋·黄石港区校级期中]如图1,在△ABC中,AD,AE分别是△ABC的高线和角平分线,若∠B=40°,∠EAD=15°,求∠C的度数.
图1
解:∵AD⊥BC,∠EAD=15°,
∴∠AED=90°-15°=75°.
∵∠AED是△ABE的外角,∠B=40°,
∴∠BAE=∠AED-∠B=75°-40°=35°.
∵AE平分∠BAC,
∴∠BAC=2∠BAE=2×35°=70°,
∴∠C=180°-∠BAC-∠B=180°-70°-40°=70°.
知识点2.三角形的中线
4.如图2,D,E分别是△ABC的边AC,BC的中点,那么下列说法中不正确的是( D )
图2
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=DC,BE=EC
D.AD=EC,DC=BE
5.三角形一边上的中线把原三角形一定分成两个( B )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
6.如图3,已知在△ABC中,CF,BE分别是AB,AC边上的中线,若AE=2,AF=3,且△ABC的周长为15,求BC的长.
图3
解:∵CF,BE分别是AB,AC边上的中线,AE=2,AF=3,
∴AB=2AF=2×3=6,AC=2AE=2×2=4,
∵△ABC的周长为15,∴BC=15-6-4=5.
7.如图4,在△ABC中,CD是中线,已知BC-AC=5 cm,△DBC的周长为25 cm,求△ADC的周长.
图4
解:∵CD是中线,∴AD=BD,
∴△DBC的周长-△ADC的周长=(BC+BD+CD)-(AC+AD+CD)=BC-AC,
∵BC-AC=5 cm,△DBC的周长为25 cm,
∴25-△ADC的周长=5,
∴△ADC的周长=20 cm.
知识点3.三角形的角平分线
8.如图5所示,AD是△ABC的角平分线,AE是△ABD的角平分线.若∠BAC=80°,则∠EAD的度数是( A )
图5
A.20°
B.30°
C.45°
D.60°
9.[2018秋·江城区期中]如图6,已知AD,CE都是△ABC的角平分线,AD,CE交于点F,∠BAC=60°,∠ACB=76°,求∠AFC的度数.
图6
解:∵AD是△ABC的角平分线,∠BAC=60°,
∴∠DAC=∠BAC=30°,
∵CE是△ABC的角平分线,∠ACB=76°,
∴∠ACF=∠ACB=38°,∴∠AFC=180°-30°-38°=112°.
【易错点】不能正确理解三角形的高线、中线和角平分线的概念.
10.三角形中:①中线、角平分线、高线都是线段;②三条高必交于一点;③三条角平分线必交于一点;④三条高必在三角形内.其中正确的是( B )
A.①② B.①③
C.②④ D.③④
综合练习
一、选择题(本题共有6小题,每小题5分,共30分)
1.[湖州校级期中]已知一个三角形的两边长分别为3和4,则第三边的长不可能的是( D )
A.2 B.3 C.4 D.1
【解析】 根据三角形的三边关系,两边之和大于第三边,两边之差小于第三边,可得1<第三边<7,故选D.
2.[杭州萧山区期末]下列各组数不可能是一个三角形的边长的是( D )
A.5,5,5 B.5,7,7
C.5,12,13 D.5,7,12
【解析】 三角形中任意两边之和大于第三边.
3.[嘉兴秀洲区校级期中]一个三角形的两个内角分别为60°和20°,则这个三角形是( C )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.不能确定
【解析】 ∵三角形的两个内角分别为60°和20°,∴第三个角为180°-60°-20°=100°,∴是钝角三角形,故选C.
4.[杭州西湖区校级期中]下列各图中,正确画出AC边上的高的是( D )
5.[宁波江北区校级期末]已知等腰三角形(有两条边相等)的其中两边长分别为4,9,则这个等腰三角形的周长是( C )
A.13 B.17
C.22 D.17或22
【解析】 分为两种情况:①当三角形的三边是4,4,9时,
∵4+4<9,
∴此时不符合三角形的三边关系定理,此时不存在三角形;
②当三角形的三边是4,9,9时,
此时符合三角形的三边关系定理,此时三角形的周长是4+9+9=22.故选C.
6.[湖州校级期中]如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的有( B )
(第6题图)
①AD是△ABE的角平分线;
②BE是△ABD的边AD上的中线;
③CH是△ACD的边AD上的高;
④AH是△ACF的角平分线和高.
A.1个 B.2个 C.3个 D.4个
【解析】 ①根据三角形的角平分线的概念,知AG是△ABE的角平分线,故此说法错误;
②根据三角形的中线的概念,知BG是△ABD的边AD上的中线,故此说法错误;
③根据三角形的高的概念,知CH为△ACD的边AD上的高,故此说法正确;
④根据三角形的角平分线和高的概念,知AH是△ACF的角平分线和高线,故此说法正确.故选B.
二、填空题(本题共有6小题,每小题5分,共30分)
7.[温州鹿城区校级期中]△ABC中,已知∠A=80°,∠B=60°,则∠C=__40°__.
【解析】 根据三角形的内角和定理可得∠C=180°-∠A-∠B=180°-80°-60°=40°.
8.[台州校级期中]如图,一副分别含有30°和45°的两个直角三角板,拼成如图图形,其中∠C=90°,∠B=45°,∠E=30°.则∠BFD的度数是__15°__.
【解析】 ∵∠EDC=60°,∴∠BDF=120°;∵∠B=45°,∴∠BFD=180°-120°-45°=15°.
(第8题图) (第9题图)
9.[嘉兴秀洲区校级期中]如图,已知BE和CF是△ABC的两条高,∠ABC=48°,∠ACB=76°,则∠FDE=__124°__.
【解析】 在△BCF中,∠BCF=180°-48°-90°=42°,
在△BCE中,∠CBE=180°-76°-90°=14°,
在△BDC中,∠BDC=180°-∠BCF-∠CBE=124°,
∴∠FDE=∠BDC=124°.
10.如图,∠ACB=90°,∠CAB=∠CBA,BE⊥CE,∠ABE=15°,则∠ACE=__60°__.
【解析】 ∵∠ACB=90°,
∴∠ABC=∠BAC=45°,
∵∠ABE=15°,∴∠CBE=60°,
∵∠BCE+∠CBE=90°,∠BCE+∠ACE=90°,
∴∠ACE=∠CBE=60°.
(第10题图) (第11题图)
11.[杭州西湖区校级期中]如图,∠1=2∠2,∠3=2∠4,∠5=2∠6,E,C,F在同一条直线上,若∠A=63°,则∠E=__21°__,∠F=__99°__.
【解析】 ∵∠A+∠ABC+∠ACB=180°,∠ACB+∠ACD=180°,
∴∠A+∠ABC=∠ACD,
∵∠1=2∠2,∠3=2∠4,
∴3∠2+∠A=3∠4,
∴∠4-∠2=∠A=×63°=21°,
∴∠E=∠4-∠2=21°,
∵∠1=2∠2,∠3=2∠4,
∴∠EBF=×180°=60°,
∴∠F=180°-∠EBF-∠E=180°-60°-21°=99°.
12.[余姚期中]如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC的面积是16 cm2,则阴影部分的面积等于__4__cm2.
(第12题图)
【解析】 ∵E为AD的中点,
∴S△ABE=S△BED,S△AEC=S△EDC,
∴S△ABC∶S△BCE=2∶1,
同理可得,S△BCE∶S△EFB=2∶1,
∵S△ABC=16,
∴S△EFB=S△ABC=×16=4.
三、解答题(本题共有4小题,共40分)
13.(10分)[绍兴柯桥区校级期中]如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
(第13题图)
解:∵AD是BC边上的高,∠EAD=5°,
∴∠AED=85°,
∵∠B=50°,
∴∠BAD=40°,
∴∠BAE=35°,
∵AE是∠BAC的角平分线,
∴∠BAC=2∠BAE=70°,
∴∠C=180°-∠B-∠BAC=180°-50°-70°=60°.
14.(10分)[青羊区校级期中]已知a,b,c分别是△ABC的三边,化简:|a+b+c|+|a+c-b|-|c-a-b|.
解:根据三角形的三边关系得a+b+c>0,a+c-b>0,c-a-b<0.
∴原式=a+b+c+a+c-b-a-b+c=a-b+3c.
15.(10分)[绍兴柯桥校级期中]平面上有n个点(n≥3),任意三点不在同一直线上,过任意三点作三角形,一共能作多少个不同的三角形?
(1)分析:当有3个点时,可作__1__个三角形;
当有4个点时,可作__4__个三角形;
当有5个点时,可作__10__个三角形…
(2)请归纳点的个数n和可以作出三角形的个数Sn的关系.
解:(1)当n=3时,可作出的三角形的个数S3==1;
当n=4时,可作出的三角形的个数S4==4;
当n=5时,可作出的三角形的个数S5==10;
(2)当点的个数是n时,可作出的三角形的个数Sn=.
16.(10分)[杭州西湖区校级期中]“综合与实践”学习活动准备制作一组三角形.记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于0且小于4的整数个单位长度,用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,3,3)表示边长分别为2,3,3个单位长度的一个三角形,请列举出所有满足条件的三角形.
解:先对a,b两条边进行取值,再根据a,b的长度结合三角形三条边之间的关系对c进行取值,列举出所有的可能性即可.当a=1,b=1时,c=1;
当a=1,b=2时,c=2;
当a=1,b=3时,c=3;
当a=2,b=2时,c=2或3;
当a=2,b=3时,c=3,
当a=3,b=3时,c=3.
所以满足条件的三角形为(1,1,1),(1,2,2),(1,3,3),(2,2,2),(2,2,3),(2,3,3),(3,3,3).
第1课时 三角形的三边关系
知识点1.三角形的概念
1.一位同学用三根木棒两两相交拼成如下图形,则其中符合三角形概念的是( )
A B C D
2.如图1所示,∠BAC的对边是( )
A.BD B.DC C.BC D.AD
图1 图2
3.如图2,图中三角形的个数为( )
A.3个 B.4个 C.5个 D.6个
知识点2.三角形的分类
4.[2018秋·开封期中]将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是直角三角形
B.都是钝角三角形
C.都是锐角三角形
D.是一个直角三角形和一个钝角三角形
5.如图3中的三角形被木板遮住了一部分,这个三角形是( )
图3
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
知识点3.三角形的三边关系
6.下列长度的三根小木棒能构成三角形的是( )
A.2 cm,3 cm,5 cm
B.7 cm,4 cm,2 cm
C.3 cm,4 cm,8 cm
D.3 cm,3 cm,4 cm
7.若一个三角形的两边长分别为3和7,则第三边长可能是( )
A.6 B.3 C.2 D.11
8.用一条长为25 cm的细绳围成一个等腰三角形,若其中有一边的长为7 cm,则该等腰三角形的腰长为__ __.
9.如图4是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板另外一个角∠C的度数为( )
图4
A.30° B.40°
C.50° D.60°
10.在△ABC中,
(1)若∠A=30°,∠B=80°,则∠C=____;
(2)若∠A=50°,∠B=∠C,则∠C=____;
(3)若∠A∶∠B∶∠C=1∶3∶5,则∠A=____,∠B=____,∠C=____.
【易错点】求与等腰三角形有关的边长时,没有指明已知边是底还是腰时,需要分类讨论,注意利用三边关系检验.
11.用一条长为20 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边长为5 cm的等腰三角形吗?如果能,请求出它的另两边的长度.
第2课时 三角形的高线、中线与角平分线
知识点1.三角形的高线
1.过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A B
C D
2.如果一个三角形两边上的高线的交点在三角形的内部,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.任意三角形
3.[2018秋·黄石港区校级期中]如图1,在△ABC中,AD,AE分别是△ABC的高线和角平分线,若∠B=40°,∠EAD=15°,求∠C的度数.
图1
知识点2.三角形的中线
4.如图2,D,E分别是△ABC的边AC,BC的中点,那么下列说法中不正确的是( )
图2
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=DC,BE=EC
D.AD=EC,DC=BE
5.三角形一边上的中线把原三角形一定分成两个( )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
6.如图3,已知在△ABC中,CF,BE分别是AB,AC边上的中线,若AE=2,AF=3,且△ABC的周长为15,求BC的长.
图3
7.如图4,在△ABC中,CD是中线,已知BC-AC=5 cm,△DBC的周长为25 cm,求△ADC的周长.
图4
知识点3.三角形的角平分线
8.如图5所示,AD是△ABC的角平分线,AE是△ABD的角平分线.若∠BAC=80°,则∠EAD的度数是( )
图5
A.20°
B.30°
C.45°
D.60°
9.[2018秋·江城区期中]如图6,已知AD,CE都是△ABC的角平分线,AD,CE交于点F,∠BAC=60°,∠ACB=76°,求∠AFC的度数.
图6
【易错点】不能正确理解三角形的高线、中线和角平分线的概念.
10.三角形中:①中线、角平分线、高线都是线段;②三条高必交于一点;③三条角平分线必交于一点;④三条高必在三角形内.其中正确的是( )
A.①② B.①③
C.②④ D.③④
综合练习
一、选择题(本题共有6小题,每小题5分,共30分)
1.[湖州校级期中]已知一个三角形的两边长分别为3和4,则第三边的长不可能的是( )
A.2 B.3 C.4 D.1
2.[杭州萧山区期末]下列各组数不可能是一个三角形的边长的是( )
A.5,5,5 B.5,7,7
C.5,12,13 D.5,7,12
3.[嘉兴秀洲区校级期中]一个三角形的两个内角分别为60°和20°,则这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.不能确定
4.[杭州西湖区校级期中]下列各图中,正确画出AC边上的高的是( )
5.[宁波江北区校级期末]已知等腰三角形(有两条边相等)的其中两边长分别为4,9,则这个等腰三角形的周长是( )
A.13 B.17
C.22 D.17或22
【
6.[湖州校级期中]如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的有( )
(第6题图)
①AD是△ABE的角平分线;
②BE是△ABD的边AD上的中线;
③CH是△ACD的边AD上的高;
④AH是△ACF的角平分线和高.
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共有6小题,每小题5分,共30分)
7.[温州鹿城区校级期中]△ABC中,已知∠A=80°,∠B=60°,则∠C=____.
8.[台州校级期中]如图,一副分别含有30°和45°的两个直角三角板,拼成如图图形,其中∠C=90°,∠B=45°,∠E=30°.则∠BFD的度数是____.
(第8题图) (第9题图)
9.[嘉兴秀洲区校级期中]如图,已知BE和CF是△ABC的两条高,∠ABC=48°,∠ACB=76°,则∠FDE=____.
10.如图,∠ACB=90°,∠CAB=∠CBA,BE⊥CE,∠ABE=15°,则∠ACE=____.
(第10题图) (第11题图)
11.[杭州西湖区校级期中]如图,∠1=2∠2,∠3=2∠4,∠5=2∠6,E,C,F在同一条直线上,若∠A=63°,则∠E=____,∠F=___.
12.[余姚期中]如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC的面积是16 cm2,则阴影部分的面积等于____cm2.
(第12题图)
三、解答题(本题共有4小题,共40分)
13.(10分)[绍兴柯桥区校级期中]如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
(第13题图)
14.(10分)[青羊区校级期中]已知a,b,c分别是△ABC的三边,化简:|a+b+c|+|a+c-b|-|c-a-b|.
15.(10分)[绍兴柯桥校级期中]平面上有n个点(n≥3),任意三点不在同一直线上,过任意三点作三角形,一共能作多少个不同的三角形?
(1)分析:当有3个点时,可作____个三角形;
当有4个点时,可作____个三角形;
当有5个点时,可作____个三角形…
(2)请归纳点的个数n和可以作出三角形的个数Sn的关系.
16.(10分)[杭州西湖区校级期中]“综合与实践”学习活动准备制作一组三角形.记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于0且小于4的整数个单位长度,用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,3,3)表示边长分别为2,3,3个单位长度的一个三角形,请列举出所有满足条件的三角形.
答案
知识点1.三角形的概念
1.一位同学用三根木棒两两相交拼成如下图形,则其中符合三角形概念的是( D )
A B C D
2.如图1所示,∠BAC的对边是( C )
A.BD B.DC C.BC D.AD
图1 图2
3.如图2,图中三角形的个数为( C )
A.3个 B.4个 C.5个 D.6个
【解析】 图中的三角形为△ABD,△ACE,△DCE,△ACD和△ABC,共5个三角形.
知识点2.三角形的分类
4.[2018秋·开封期中]将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( C )
A.都是直角三角形
B.都是钝角三角形
C.都是锐角三角形
D.是一个直角三角形和一个钝角三角形
【解析】 如答图①,沿三角形一边上的高剪开即可得到两个直角三角形;
① ② ③
第4题答图
如答图②,钝角三角形沿虚线剪开即可得到两个钝角三角形;
如答图③,直角三角形沿虚线剪开即可得到一个直角三角形和一个钝角三角形.
∵剪开的边上的两个角互补,故这两个三角形不可能都是锐角三角形.
5.如图3中的三角形被木板遮住了一部分,这个三角形是( D )
图3
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
知识点3.三角形的三边关系
6.下列长度的三根小木棒能构成三角形的是( D )
A.2 cm,3 cm,5 cm
B.7 cm,4 cm,2 cm
C.3 cm,4 cm,8 cm
D.3 cm,3 cm,4 cm
7.若一个三角形的两边长分别为3和7,则第三边长可能是( A )
A.6 B.3 C.2 D.11
8.用一条长为25 cm的细绳围成一个等腰三角形,若其中有一边的长为7 cm,则该等腰三角形的腰长为__7 cm或9 cm__.
【解析】 7 cm是腰长时,底边为25-7×2=11,
∵7+7>11,∴7 cm,7 cm,11 cm能组成三角形;
7 cm是底边时,腰长为×(25-7)=9 cm,
7 cm,9 cm,9 cm能够组成三角形.
综上所述,它的腰长为7 cm或9 cm.
知识点4.三角形的内角和定理
9.如图4是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板另外一个角∠C的度数为( B )
图4
A.30° B.40°
C.50° D.60°
10.在△ABC中,
(1)若∠A=30°,∠B=80°,则∠C=__70°__;
(2)若∠A=50°,∠B=∠C,则∠C=__65°__;
(3)若∠A∶∠B∶∠C=1∶3∶5,则∠A=__20°__,∠B=__60°__,∠C=__100°__.
【易错点】求与等腰三角形有关的边长时,没有指明已知边是底还是腰时,需要分类讨论,注意利用三边关系检验.
11.用一条长为20 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边长为5 cm的等腰三角形吗?如果能,请求出它的另两边的长度.
解:(1)设底边长为x cm,则腰长为2x cm,则
2x+2x+x=20,解得x=4,
∴2x=8,∴各边长为8 cm,8 cm,4 cm;
(2)①当5 cm为底时,腰长=7.5 cm;
②当5 cm为腰时,底边=10 cm,∵5+5=10,故不能构成三角形,舍去.
∴能构成有一边长为5 cm的等腰三角形,另两边长为7.5 cm,7.5 cm.
第2课时 三角形的高线、中线与角平分线
知识点1.三角形的高线
1.过△ABC的顶点A,作BC边上的高,以下作法正确的是( A )
A B
C D
2.如果一个三角形两边上的高线的交点在三角形的内部,那么这个三角形是( A )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.任意三角形
3.[2018秋·黄石港区校级期中]如图1,在△ABC中,AD,AE分别是△ABC的高线和角平分线,若∠B=40°,∠EAD=15°,求∠C的度数.
图1
解:∵AD⊥BC,∠EAD=15°,
∴∠AED=90°-15°=75°.
∵∠AED是△ABE的外角,∠B=40°,
∴∠BAE=∠AED-∠B=75°-40°=35°.
∵AE平分∠BAC,
∴∠BAC=2∠BAE=2×35°=70°,
∴∠C=180°-∠BAC-∠B=180°-70°-40°=70°.
知识点2.三角形的中线
4.如图2,D,E分别是△ABC的边AC,BC的中点,那么下列说法中不正确的是( D )
图2
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=DC,BE=EC
D.AD=EC,DC=BE
5.三角形一边上的中线把原三角形一定分成两个( B )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
6.如图3,已知在△ABC中,CF,BE分别是AB,AC边上的中线,若AE=2,AF=3,且△ABC的周长为15,求BC的长.
图3
解:∵CF,BE分别是AB,AC边上的中线,AE=2,AF=3,
∴AB=2AF=2×3=6,AC=2AE=2×2=4,
∵△ABC的周长为15,∴BC=15-6-4=5.
7.如图4,在△ABC中,CD是中线,已知BC-AC=5 cm,△DBC的周长为25 cm,求△ADC的周长.
图4
解:∵CD是中线,∴AD=BD,
∴△DBC的周长-△ADC的周长=(BC+BD+CD)-(AC+AD+CD)=BC-AC,
∵BC-AC=5 cm,△DBC的周长为25 cm,
∴25-△ADC的周长=5,
∴△ADC的周长=20 cm.
知识点3.三角形的角平分线
8.如图5所示,AD是△ABC的角平分线,AE是△ABD的角平分线.若∠BAC=80°,则∠EAD的度数是( A )
图5
A.20°
B.30°
C.45°
D.60°
9.[2018秋·江城区期中]如图6,已知AD,CE都是△ABC的角平分线,AD,CE交于点F,∠BAC=60°,∠ACB=76°,求∠AFC的度数.
图6
解:∵AD是△ABC的角平分线,∠BAC=60°,
∴∠DAC=∠BAC=30°,
∵CE是△ABC的角平分线,∠ACB=76°,
∴∠ACF=∠ACB=38°,∴∠AFC=180°-30°-38°=112°.
【易错点】不能正确理解三角形的高线、中线和角平分线的概念.
10.三角形中:①中线、角平分线、高线都是线段;②三条高必交于一点;③三条角平分线必交于一点;④三条高必在三角形内.其中正确的是( B )
A.①② B.①③
C.②④ D.③④
综合练习
一、选择题(本题共有6小题,每小题5分,共30分)
1.[湖州校级期中]已知一个三角形的两边长分别为3和4,则第三边的长不可能的是( D )
A.2 B.3 C.4 D.1
【解析】 根据三角形的三边关系,两边之和大于第三边,两边之差小于第三边,可得1<第三边<7,故选D.
2.[杭州萧山区期末]下列各组数不可能是一个三角形的边长的是( D )
A.5,5,5 B.5,7,7
C.5,12,13 D.5,7,12
【解析】 三角形中任意两边之和大于第三边.
3.[嘉兴秀洲区校级期中]一个三角形的两个内角分别为60°和20°,则这个三角形是( C )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.不能确定
【解析】 ∵三角形的两个内角分别为60°和20°,∴第三个角为180°-60°-20°=100°,∴是钝角三角形,故选C.
4.[杭州西湖区校级期中]下列各图中,正确画出AC边上的高的是( D )
5.[宁波江北区校级期末]已知等腰三角形(有两条边相等)的其中两边长分别为4,9,则这个等腰三角形的周长是( C )
A.13 B.17
C.22 D.17或22
【解析】 分为两种情况:①当三角形的三边是4,4,9时,
∵4+4<9,
∴此时不符合三角形的三边关系定理,此时不存在三角形;
②当三角形的三边是4,9,9时,
此时符合三角形的三边关系定理,此时三角形的周长是4+9+9=22.故选C.
6.[湖州校级期中]如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的有( B )
(第6题图)
①AD是△ABE的角平分线;
②BE是△ABD的边AD上的中线;
③CH是△ACD的边AD上的高;
④AH是△ACF的角平分线和高.
A.1个 B.2个 C.3个 D.4个
【解析】 ①根据三角形的角平分线的概念,知AG是△ABE的角平分线,故此说法错误;
②根据三角形的中线的概念,知BG是△ABD的边AD上的中线,故此说法错误;
③根据三角形的高的概念,知CH为△ACD的边AD上的高,故此说法正确;
④根据三角形的角平分线和高的概念,知AH是△ACF的角平分线和高线,故此说法正确.故选B.
二、填空题(本题共有6小题,每小题5分,共30分)
7.[温州鹿城区校级期中]△ABC中,已知∠A=80°,∠B=60°,则∠C=__40°__.
【解析】 根据三角形的内角和定理可得∠C=180°-∠A-∠B=180°-80°-60°=40°.
8.[台州校级期中]如图,一副分别含有30°和45°的两个直角三角板,拼成如图图形,其中∠C=90°,∠B=45°,∠E=30°.则∠BFD的度数是__15°__.
【解析】 ∵∠EDC=60°,∴∠BDF=120°;∵∠B=45°,∴∠BFD=180°-120°-45°=15°.
(第8题图) (第9题图)
9.[嘉兴秀洲区校级期中]如图,已知BE和CF是△ABC的两条高,∠ABC=48°,∠ACB=76°,则∠FDE=__124°__.
【解析】 在△BCF中,∠BCF=180°-48°-90°=42°,
在△BCE中,∠CBE=180°-76°-90°=14°,
在△BDC中,∠BDC=180°-∠BCF-∠CBE=124°,
∴∠FDE=∠BDC=124°.
10.如图,∠ACB=90°,∠CAB=∠CBA,BE⊥CE,∠ABE=15°,则∠ACE=__60°__.
【解析】 ∵∠ACB=90°,
∴∠ABC=∠BAC=45°,
∵∠ABE=15°,∴∠CBE=60°,
∵∠BCE+∠CBE=90°,∠BCE+∠ACE=90°,
∴∠ACE=∠CBE=60°.
(第10题图) (第11题图)
11.[杭州西湖区校级期中]如图,∠1=2∠2,∠3=2∠4,∠5=2∠6,E,C,F在同一条直线上,若∠A=63°,则∠E=__21°__,∠F=__99°__.
【解析】 ∵∠A+∠ABC+∠ACB=180°,∠ACB+∠ACD=180°,
∴∠A+∠ABC=∠ACD,
∵∠1=2∠2,∠3=2∠4,
∴3∠2+∠A=3∠4,
∴∠4-∠2=∠A=×63°=21°,
∴∠E=∠4-∠2=21°,
∵∠1=2∠2,∠3=2∠4,
∴∠EBF=×180°=60°,
∴∠F=180°-∠EBF-∠E=180°-60°-21°=99°.
12.[余姚期中]如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC的面积是16 cm2,则阴影部分的面积等于__4__cm2.
(第12题图)
【解析】 ∵E为AD的中点,
∴S△ABE=S△BED,S△AEC=S△EDC,
∴S△ABC∶S△BCE=2∶1,
同理可得,S△BCE∶S△EFB=2∶1,
∵S△ABC=16,
∴S△EFB=S△ABC=×16=4.
三、解答题(本题共有4小题,共40分)
13.(10分)[绍兴柯桥区校级期中]如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
(第13题图)
解:∵AD是BC边上的高,∠EAD=5°,
∴∠AED=85°,
∵∠B=50°,
∴∠BAD=40°,
∴∠BAE=35°,
∵AE是∠BAC的角平分线,
∴∠BAC=2∠BAE=70°,
∴∠C=180°-∠B-∠BAC=180°-50°-70°=60°.
14.(10分)[青羊区校级期中]已知a,b,c分别是△ABC的三边,化简:|a+b+c|+|a+c-b|-|c-a-b|.
解:根据三角形的三边关系得a+b+c>0,a+c-b>0,c-a-b<0.
∴原式=a+b+c+a+c-b-a-b+c=a-b+3c.
15.(10分)[绍兴柯桥校级期中]平面上有n个点(n≥3),任意三点不在同一直线上,过任意三点作三角形,一共能作多少个不同的三角形?
(1)分析:当有3个点时,可作__1__个三角形;
当有4个点时,可作__4__个三角形;
当有5个点时,可作__10__个三角形…
(2)请归纳点的个数n和可以作出三角形的个数Sn的关系.
解:(1)当n=3时,可作出的三角形的个数S3==1;
当n=4时,可作出的三角形的个数S4==4;
当n=5时,可作出的三角形的个数S5==10;
(2)当点的个数是n时,可作出的三角形的个数Sn=.
16.(10分)[杭州西湖区校级期中]“综合与实践”学习活动准备制作一组三角形.记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于0且小于4的整数个单位长度,用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,3,3)表示边长分别为2,3,3个单位长度的一个三角形,请列举出所有满足条件的三角形.
解:先对a,b两条边进行取值,再根据a,b的长度结合三角形三条边之间的关系对c进行取值,列举出所有的可能性即可.当a=1,b=1时,c=1;
当a=1,b=2时,c=2;
当a=1,b=3时,c=3;
当a=2,b=2时,c=2或3;
当a=2,b=3时,c=3,
当a=3,b=3时,c=3.
所以满足条件的三角形为(1,1,1),(1,2,2),(1,3,3),(2,2,2),(2,2,3),(2,3,3),(3,3,3).
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
