浙教版数学八上1.3同步练习(共2课时、含答案)
文档属性
| 名称 | 浙教版数学八上1.3同步练习(共2课时、含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 152.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 13:59:48 | ||
图片预览


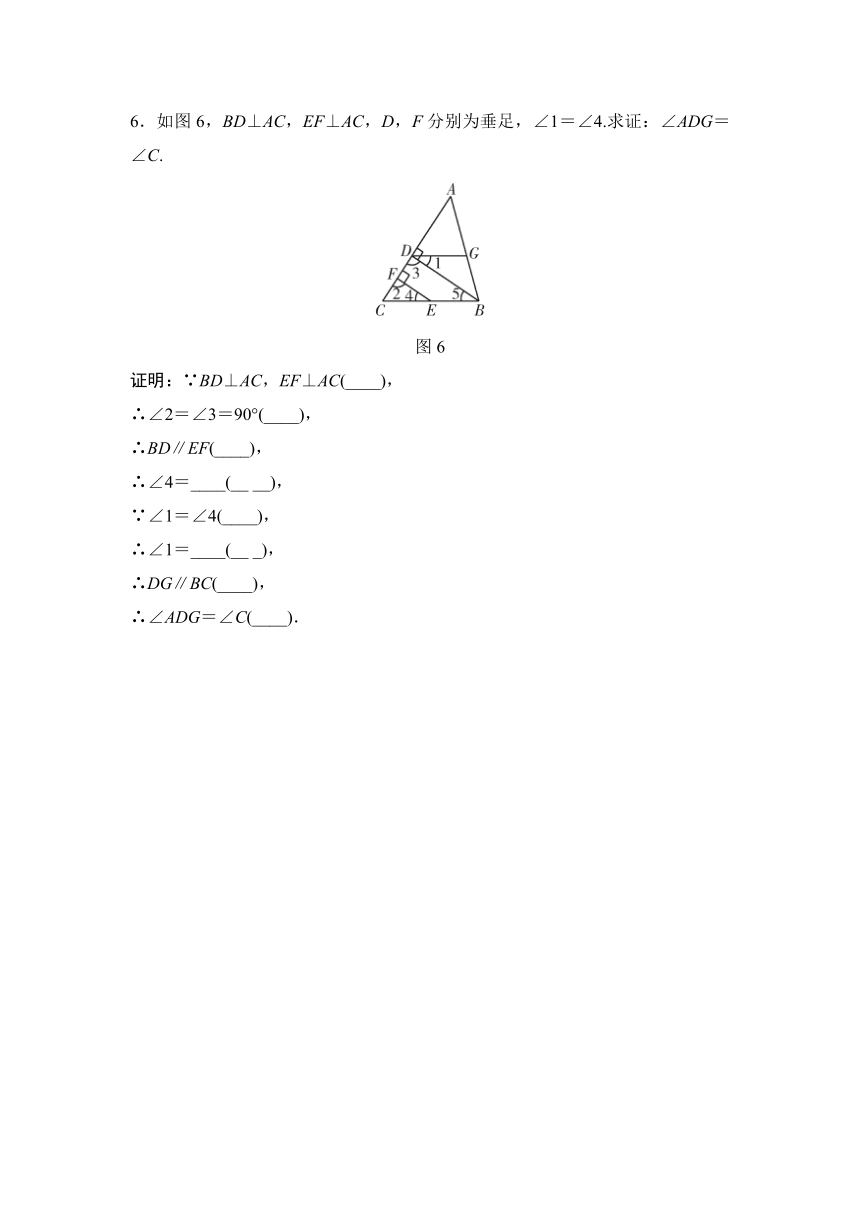

文档简介
1.3 证明
第1课时 平行线的性质与判定
知识点1.证明的概念
1.如图1,已知:AB∥CD,∠D=∠B,问AD∥BC吗?为什么?
图1
解:∵AB∥CD(已知),
∴∠B+___ =180°(____),
∵∠D=∠B(已知),
∴___+____=180°(等量代换),
∴____∥____(__ __).
2.[2018秋·兰州期末]如图2,∠ABC=∠ADC,BF,DE分别是∠ABC,∠ADC的角平分线,∠1=∠2,求证:DC∥AB.
图2
知识点2.平行线的性质与判定
3.[2018秋·宽城区期末]如图3,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )
图3
A.∠2=∠4
B.∠4=∠5
C.∠1=∠3
D.∠1+∠4=180°
4.[2018春·仓山区期中]如图4,点E在AC的延长线上,下列条件能判断AB∥CD的是( )
图4
A.∠1=∠2
B.∠3=∠4
C.∠D=∠DCE
D.∠D+∠ACD=180°
5.[2018春·桥西区校级期中]如图5,已知∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
图5
【易错点】不能正确地写出证明中每一步的理由.
6.如图6,BD⊥AC,EF⊥AC,D,F分别为垂足,∠1=∠4.求证:∠ADG=∠C.
图6
证明:∵BD⊥AC,EF⊥AC(____),
∴∠2=∠3=90°(____),
∴BD∥EF(____),
∴∠4=____(__ __),
∵∠1=∠4(____),
∴∠1=____(__ _),
∴DG∥BC(____),
∴∠ADG=∠C(____).
第2课时 三角形的内角和定理及推论
知识点1.三角形内角和定理
1.在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( )
A.35° B.40°
C.45° D.50°
2.如图1,在△ABC中,∠A=46°,CE是∠ACB的平分线,B,C,D在同一条直线上,DF∥EC,∠D=42°.求∠B的度数.
图1
3.如图2,按规定,一块模板中AB,CD的延长线应相交成85°角.因交点不在板上,不便测量,工人师傅连结AC,测得∠BAC=32°,∠DCA=65°,此时AB,CD的延长线相交所成的角是否符合规定?为什么?
图2
知识点2.三角形的外角的性质
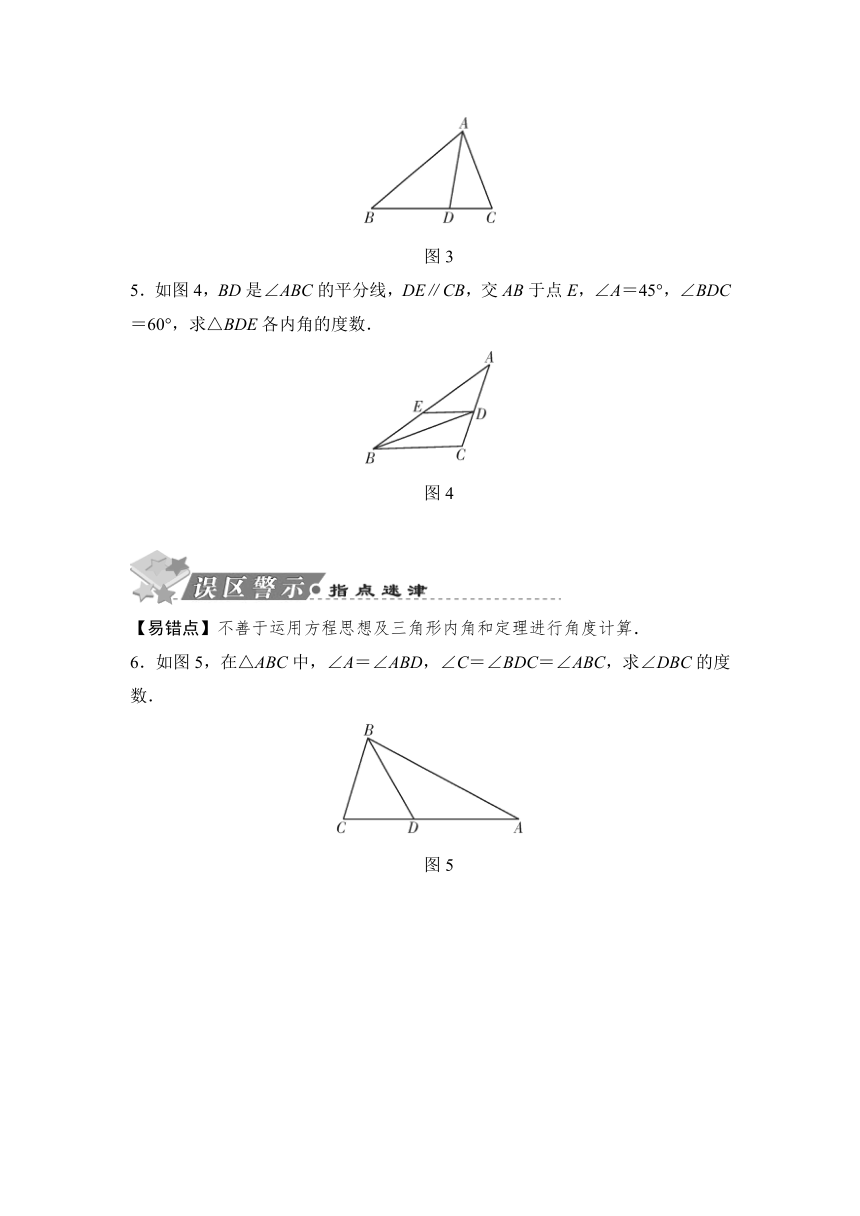
4.如图3,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.求:
(1)∠B的度数;
(2)∠C的度数.
图3
5.如图4,BD是∠ABC的平分线,DE∥CB,交AB于点E,∠A=45°,∠BDC=60°,求△BDE各内角的度数.
图4
【易错点】不善于运用方程思想及三角形内角和定理进行角度计算.
6.如图5,在△ABC中,∠A=∠ABD,∠C=∠BDC=∠ABC,求∠DBC的度数.
图5
答案
第1课时 平行线的性质与判定
知识点1.证明的概念
1.如图1,已知:AB∥CD,∠D=∠B,问AD∥BC吗?为什么?
图1
解:∵AB∥CD(已知),
∴∠B+__∠C__ =180°(__两直线平行,同旁内角互补__),
∵∠D=∠B(已知),
∴__∠C__+__∠D__=180°(等量代换),
∴__AD__∥__BC__(__同旁内角互补,两直线平行__).
2.[2018秋·兰州期末]如图2,∠ABC=∠ADC,BF,DE分别是∠ABC,∠ADC的角平分线,∠1=∠2,求证:DC∥AB.
图2
证明:∵BF,DE分别是∠ABC,∠ADC的角平分线,
∴∠EDC=∠ADC,∠2=∠ABC,
∵∠ABC=∠ADC,∴∠EDC=∠2,
∵∠1=∠2,∴∠1=∠EDC,∴DC∥AB.
知识点2.平行线的性质与判定
3.[2018秋·宽城区期末]如图3,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( C )
图3
A.∠2=∠4
B.∠4=∠5
C.∠1=∠3
D.∠1+∠4=180°
4.[2018春·仓山区期中]如图4,点E在AC的延长线上,下列条件能判断AB∥CD的是( A )
图4
A.∠1=∠2
B.∠3=∠4
C.∠D=∠DCE
D.∠D+∠ACD=180°
5.[2018春·桥西区校级期中]如图5,已知∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
图5
证明:∵∠ABC+∠ECB=180°,
∴AB∥DE,∴∠ABC=∠BCD,
∵∠P=∠Q,∴PB∥CQ,
∴∠PBC=∠BCQ,
∵∠1=∠ABC-∠PBC,∠2=∠BCD-∠BCQ,
∴∠1=∠2.
【易错点】不能正确地写出证明中每一步的理由.
6.如图6,BD⊥AC,EF⊥AC,D,F分别为垂足,∠1=∠4.求证:∠ADG=∠C.
图6
证明:∵BD⊥AC,EF⊥AC(__已知__),
∴∠2=∠3=90°(__垂直的定义__),
∴BD∥EF(__同位角相等,两直线平行__),
∴∠4=__∠5__(__两直线平行,同位角相等__),
∵∠1=∠4(__已知__),
∴∠1=__∠5__(__等量代换__),
∴DG∥BC(__内错角相等,两直线平行__),
∴∠ADG=∠C(__两直线平行,同位角相等__).
第2课时 三角形的内角和定理及推论
知识点1.三角形内角和定理
1.在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( C )
A.35° B.40°
C.45° D.50°
2.如图1,在△ABC中,∠A=46°,CE是∠ACB的平分线,B,C,D在同一条直线上,DF∥EC,∠D=42°.求∠B的度数.
图1
解:∵DF∥EC,∴∠BCE=∠D=42°.
∵CE是∠ACB的平分线,∴∠ACB=2∠BCE=84°.
∵∠A=46°,∴∠B=180°-84°-46°=50°.
3.如图2,按规定,一块模板中AB,CD的延长线应相交成85°角.因交点不在板上,不便测量,工人师傅连结AC,测得∠BAC=32°,∠DCA=65°,此时AB,CD的延长线相交所成的角是否符合规定?为什么?
图2
解:不符合规定.延长AB,CD交于点O,
∵△AOC中,∠BAC=32°,∠DCA=65°,
∴∠AOC=180°-∠BAC-∠DCA=180°-32°-65°=83°<85°.
∴模板不符合规定.
知识点2.三角形的外角的性质
4.如图3,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.求:
(1)∠B的度数;
(2)∠C的度数.
图3
解:(1)∵∠ADC=∠B+∠BAD=80°(三角形的一个外角等于与它不相邻的两个内角的和),且∠B=∠BAD,∴∠B=40°;
(2)∵∠BAC+∠B+∠C=180°(三角形内角和定理),∠BAC=70°,∠B=40°,∴∠C=70°.
5.如图4,BD是∠ABC的平分线,DE∥CB,交AB于点E,∠A=45°,∠BDC=60°,求△BDE各内角的度数.
图4
解:∵∠A=45°,∠BDC=60°,
∴∠ABD=∠BDC-∠A=15°.
∵BD是∠ABC的角平分线,
∴∠DBC=∠EBD=15°,
∵DE∥BC,∴∠BDE=∠DBC=15°,
∴∠BED=180°-∠EBD-∠EDB=150°.
【易错点】不善于运用方程思想及三角形内角和定理进行角度计算.
6.如图5,在△ABC中,∠A=∠ABD,∠C=∠BDC=∠ABC,求∠DBC的度数.
图5
解:设∠A=x,
∵∠A=∠ABD,∴∠A=∠ABD=x,∴∠BDC=∠A+∠ABD=2x.
∵∠C=∠BDC=∠ABC,∴∠C=∠BDC=∠ABC=2x,∴∠DBC=x.
∵∠A+∠ABC+∠C=180°,即x+2x+2x=180°,解得x=36°,
∴∠DBC=36°.
第1课时 平行线的性质与判定
知识点1.证明的概念
1.如图1,已知:AB∥CD,∠D=∠B,问AD∥BC吗?为什么?
图1
解:∵AB∥CD(已知),
∴∠B+___ =180°(____),
∵∠D=∠B(已知),
∴___+____=180°(等量代换),
∴____∥____(__ __).
2.[2018秋·兰州期末]如图2,∠ABC=∠ADC,BF,DE分别是∠ABC,∠ADC的角平分线,∠1=∠2,求证:DC∥AB.
图2
知识点2.平行线的性质与判定
3.[2018秋·宽城区期末]如图3,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )
图3
A.∠2=∠4
B.∠4=∠5
C.∠1=∠3
D.∠1+∠4=180°
4.[2018春·仓山区期中]如图4,点E在AC的延长线上,下列条件能判断AB∥CD的是( )
图4
A.∠1=∠2
B.∠3=∠4
C.∠D=∠DCE
D.∠D+∠ACD=180°
5.[2018春·桥西区校级期中]如图5,已知∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
图5
【易错点】不能正确地写出证明中每一步的理由.
6.如图6,BD⊥AC,EF⊥AC,D,F分别为垂足,∠1=∠4.求证:∠ADG=∠C.
图6
证明:∵BD⊥AC,EF⊥AC(____),
∴∠2=∠3=90°(____),
∴BD∥EF(____),
∴∠4=____(__ __),
∵∠1=∠4(____),
∴∠1=____(__ _),
∴DG∥BC(____),
∴∠ADG=∠C(____).
第2课时 三角形的内角和定理及推论
知识点1.三角形内角和定理
1.在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( )
A.35° B.40°
C.45° D.50°
2.如图1,在△ABC中,∠A=46°,CE是∠ACB的平分线,B,C,D在同一条直线上,DF∥EC,∠D=42°.求∠B的度数.
图1
3.如图2,按规定,一块模板中AB,CD的延长线应相交成85°角.因交点不在板上,不便测量,工人师傅连结AC,测得∠BAC=32°,∠DCA=65°,此时AB,CD的延长线相交所成的角是否符合规定?为什么?
图2
知识点2.三角形的外角的性质
4.如图3,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.求:
(1)∠B的度数;
(2)∠C的度数.
图3
5.如图4,BD是∠ABC的平分线,DE∥CB,交AB于点E,∠A=45°,∠BDC=60°,求△BDE各内角的度数.
图4
【易错点】不善于运用方程思想及三角形内角和定理进行角度计算.
6.如图5,在△ABC中,∠A=∠ABD,∠C=∠BDC=∠ABC,求∠DBC的度数.
图5
答案
第1课时 平行线的性质与判定
知识点1.证明的概念
1.如图1,已知:AB∥CD,∠D=∠B,问AD∥BC吗?为什么?
图1
解:∵AB∥CD(已知),
∴∠B+__∠C__ =180°(__两直线平行,同旁内角互补__),
∵∠D=∠B(已知),
∴__∠C__+__∠D__=180°(等量代换),
∴__AD__∥__BC__(__同旁内角互补,两直线平行__).
2.[2018秋·兰州期末]如图2,∠ABC=∠ADC,BF,DE分别是∠ABC,∠ADC的角平分线,∠1=∠2,求证:DC∥AB.
图2
证明:∵BF,DE分别是∠ABC,∠ADC的角平分线,
∴∠EDC=∠ADC,∠2=∠ABC,
∵∠ABC=∠ADC,∴∠EDC=∠2,
∵∠1=∠2,∴∠1=∠EDC,∴DC∥AB.
知识点2.平行线的性质与判定
3.[2018秋·宽城区期末]如图3,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( C )
图3
A.∠2=∠4
B.∠4=∠5
C.∠1=∠3
D.∠1+∠4=180°
4.[2018春·仓山区期中]如图4,点E在AC的延长线上,下列条件能判断AB∥CD的是( A )
图4
A.∠1=∠2
B.∠3=∠4
C.∠D=∠DCE
D.∠D+∠ACD=180°
5.[2018春·桥西区校级期中]如图5,已知∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
图5
证明:∵∠ABC+∠ECB=180°,
∴AB∥DE,∴∠ABC=∠BCD,
∵∠P=∠Q,∴PB∥CQ,
∴∠PBC=∠BCQ,
∵∠1=∠ABC-∠PBC,∠2=∠BCD-∠BCQ,
∴∠1=∠2.
【易错点】不能正确地写出证明中每一步的理由.
6.如图6,BD⊥AC,EF⊥AC,D,F分别为垂足,∠1=∠4.求证:∠ADG=∠C.
图6
证明:∵BD⊥AC,EF⊥AC(__已知__),
∴∠2=∠3=90°(__垂直的定义__),
∴BD∥EF(__同位角相等,两直线平行__),
∴∠4=__∠5__(__两直线平行,同位角相等__),
∵∠1=∠4(__已知__),
∴∠1=__∠5__(__等量代换__),
∴DG∥BC(__内错角相等,两直线平行__),
∴∠ADG=∠C(__两直线平行,同位角相等__).
第2课时 三角形的内角和定理及推论
知识点1.三角形内角和定理
1.在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( C )
A.35° B.40°
C.45° D.50°
2.如图1,在△ABC中,∠A=46°,CE是∠ACB的平分线,B,C,D在同一条直线上,DF∥EC,∠D=42°.求∠B的度数.
图1
解:∵DF∥EC,∴∠BCE=∠D=42°.
∵CE是∠ACB的平分线,∴∠ACB=2∠BCE=84°.
∵∠A=46°,∴∠B=180°-84°-46°=50°.
3.如图2,按规定,一块模板中AB,CD的延长线应相交成85°角.因交点不在板上,不便测量,工人师傅连结AC,测得∠BAC=32°,∠DCA=65°,此时AB,CD的延长线相交所成的角是否符合规定?为什么?
图2
解:不符合规定.延长AB,CD交于点O,
∵△AOC中,∠BAC=32°,∠DCA=65°,
∴∠AOC=180°-∠BAC-∠DCA=180°-32°-65°=83°<85°.
∴模板不符合规定.
知识点2.三角形的外角的性质
4.如图3,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.求:
(1)∠B的度数;
(2)∠C的度数.
图3
解:(1)∵∠ADC=∠B+∠BAD=80°(三角形的一个外角等于与它不相邻的两个内角的和),且∠B=∠BAD,∴∠B=40°;
(2)∵∠BAC+∠B+∠C=180°(三角形内角和定理),∠BAC=70°,∠B=40°,∴∠C=70°.
5.如图4,BD是∠ABC的平分线,DE∥CB,交AB于点E,∠A=45°,∠BDC=60°,求△BDE各内角的度数.
图4
解:∵∠A=45°,∠BDC=60°,
∴∠ABD=∠BDC-∠A=15°.
∵BD是∠ABC的角平分线,
∴∠DBC=∠EBD=15°,
∵DE∥BC,∴∠BDE=∠DBC=15°,
∴∠BED=180°-∠EBD-∠EDB=150°.
【易错点】不善于运用方程思想及三角形内角和定理进行角度计算.
6.如图5,在△ABC中,∠A=∠ABD,∠C=∠BDC=∠ABC,求∠DBC的度数.
图5
解:设∠A=x,
∵∠A=∠ABD,∴∠A=∠ABD=x,∴∠BDC=∠A+∠ABD=2x.
∵∠C=∠BDC=∠ABC,∴∠C=∠BDC=∠ABC=2x,∴∠DBC=x.
∵∠A+∠ABC+∠C=180°,即x+2x+2x=180°,解得x=36°,
∴∠DBC=36°.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
