浙教版数学八上1.5三角形全等的判定 同步练习(4课时打包,含答案)
文档属性
| 名称 | 浙教版数学八上1.5三角形全等的判定 同步练习(4课时打包,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 358.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-19 13:59:31 | ||
图片预览



文档简介
1.5三角形全等的判定
第1课时 “边边边”
知识点1.三角形全等的判定(SSS)
1.如图1所示,如果AB=A′B′,BC=B′C′,AC=A′C′,则下列结论正确的是( )
图1
A.△ABC≌△A′B′C′
B.△ABC≌△C′A′B′
C.△ABC≌△B′C′A′
D.这两个三角形不全等
2.下列三角形中,与图2中△ABC全等的是____.
3.如图3所示,AD=BC,AC=BD,用三角形全等的判定“SSS”可证明__ __≌__ __或____≌__ __.
图3
知识点2.三角形的稳定性
4.[2018春·泉港区期末]如图4,人字梯中间一般会设计一“拉杆”,这样做的道理是( )
图4
A.两点之间,线段最短
B.垂线段最短
C.三角形具有稳定性
D.两直线平行,内错角相等
知识点3.三角形全等的判定与性质的综合
5.在△ABC和△A1B1C1中,AB=A1B1,BC=B1C1,AC=A1C1,且∠A=110°,∠B=40°,则∠C1=( )
A.110° B.40° C.30° D.20°
6.如图5所示,在△ABC和△DBC中,已知AB=DB,AC=DC,则下列结论中错误的是( )
图5
A.△ABC≌△DBC
B.∠A=∠D
C.BC是∠ACD的平分线
D.∠A=∠BCD
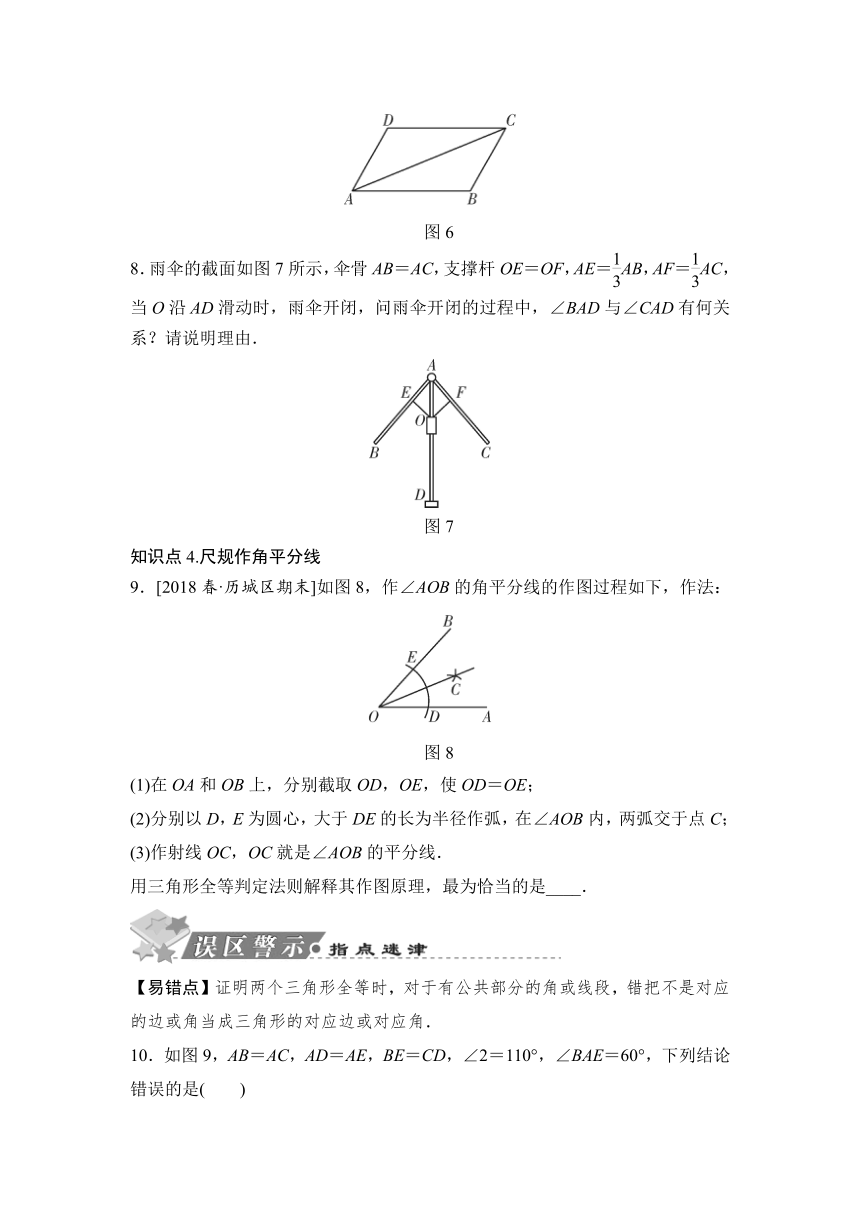
7.如图6,在四边形ABCD中,AB=CD,AD=CB,连结AC,求证:∠ACD=∠CAB.
图6
8.雨伞的截面如图7所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭的过程中,∠BAD与∠CAD有何关系?请说明理由.
图7
知识点4.尺规作角平分线
9.[2018春·历城区期末]如图8,作∠AOB的角平分线的作图过程如下,作法:
图8
(1)在OA和OB上,分别截取OD,OE,使OD=OE;
(2)分别以D,E为圆心,大于DE的长为半径作弧,在∠AOB内,两弧交于点C;
(3)作射线OC,OC就是∠AOB的平分线.
用三角形全等判定法则解释其作图原理,最为恰当的是____.
【易错点】证明两个三角形全等时,对于有公共部分的角或线段,错把不是对应的边或角当成三角形的对应边或对应角.
10.如图9,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,下列结论错误的是( )
图9
A.△ABE≌△ACD
B.△ABD≌△ACE
C.∠ACE=30°
D.∠1=70°
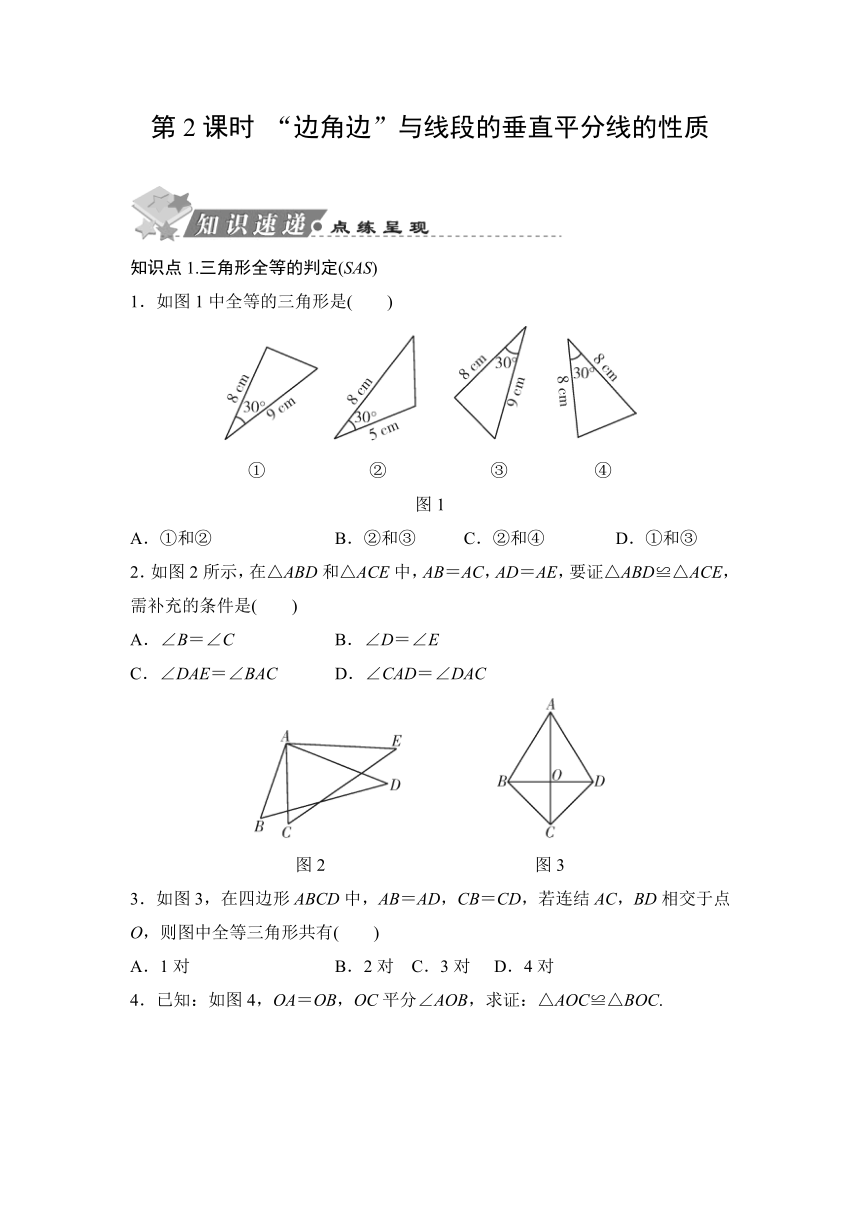
第2课时 “边角边”与线段的垂直平分线的性质
知识点1.三角形全等的判定(SAS)
1.如图1中全等的三角形是( )
① ② ③ ④
图1
A.①和② B.②和③ C.②和④ D.①和③
2.如图2所示,在△ABD和△ACE中,AB=AC,AD=AE,要证△ABD≌△ACE,需补充的条件是( )
A.∠B=∠C B.∠D=∠E
C.∠DAE=∠BAC D.∠CAD=∠DAC
图2 图3
3.如图3,在四边形ABCD中,AB=AD,CB=CD,若连结AC,BD相交于点O,则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
4.已知:如图4,OA=OB,OC平分∠AOB,求证:△AOC≌△BOC.
图4
知识点2.利用“SAS”判定三角形全等证明线段或角相等
5.如图5,在△ABC和△ABD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA,求证:AC=BD.
图5
6.如图6,在△ABC中,已知AB=AC,AD平分∠BAC,点M,N分别在AB,AC边上,AM=2MB,AN=2NC.求证:DM=DN.
图6
知识点3.利用“SAS”判定三角形全等来解决实际问题
7.如图7所示,有一块三角形镜子,小明不小心将它打破成Ⅰ,Ⅱ两块,现需配成同样大小的一块.为了方便起见,需带上____块,其理由是__ __.
图7
知识点4.线段的垂直平分线的性质
8.[2017秋·浉河区期末]如图8,DE是△ABC中AC边的垂直平分线,若BC=8,AB=10,则△EBC的周长是( )
A.13 B.16 C.18 D.20
图8 图9
9.如图9,在△ABC中,AB=AC=20 cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为 35 cm,则BC的长为( C )
A.5 cm B.10 cm
C.15 cm D.17.5 cm
【易错点】“SSA”不能判定两个三角形全等.
10.下列条件能够判断△ABC与△A′B′C全等的是( )
A.∠A=∠A′
B.AB=A′B′,∠B=∠B′,AC=A′C′
C.AB=A′B′,AC=A′C′
D.AB=A′B′,∠A=∠A′,AC=A′C′
第3课时 “角边角”
知识点 三角形全等的判定(ASA)
1.如图1,已知△ABC三条边、三个角,则甲、乙两个三角形中和△ABC全等的图形是( )
图1
A.甲 B.乙
C.甲和乙都是 D.都不是
2.如图2所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是__ __.
图2
3.如图3,∠1=∠2,∠3=∠4,求证:AC=AD.
图3
4.[2018秋·延庆区期中]如图4,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,且∠B=∠C.求证:△ABE≌△ACD.
图4
5.[2018秋·金坛区期中]如图5,在△ABC和△ADE中,AB=AD,∠B=∠D,∠1=∠2.求证:△ABC≌△ADE.
图5
【易错点】错用判定三角形全等的判定方法.
6.已知:如图6,∠AOD=∠BOC,∠A=∠C,O是AC的中点.求证:△AOB≌△COD.
图6
第4课时 “角角边”与角平分线的性质
知识点1.三角形全等的判定(AAS)
1.如图1,AB=AE,∠1=∠2,∠C=∠D.求证:△ABC≌△AED.
图1
2.如图2,已知:在△AFD和△CEB中,点A,E,F,C在同一直线上,AE=CF,∠B=∠D,AD∥BC.求证:AD=BC.
图2
知识点2.三角形全等判定方法的选用
3.如图3,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
A.AC=BD B.∠CAB=∠DBA
C.∠C=∠D D.BC=AD
图3 图4
4.如图4所示,在△ABC中,∠B=∠C,D为BC边的中点,过点D分别向AB,AC作垂线段,则能够说明△BDE≌△CDF的理由是( )
A.SSS B.SAS C.ASA D.AAS
知识点3.角平分线的性质
5.如图5,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
图5
A.6 B.5 C.4 D.3
6.[2019·辽阳模拟]如图6,BD平分∠ABC,DE⊥BC于点E,AB=7,DE=4,则S△ABD=( )
A.28 B.21
C.14 D.7
图6
7.如图7,已知BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.
图7
【易错点】对于全等三角形开放性问题,常常不能正确选用判定方法.
8. 如图8,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
图8
A.∠A=∠D B.BC=EF
C.∠ACB=∠F D.AC=DF
答案
第1课时 “边边边”
知识点1.三角形全等的判定(SSS)
1.如图1所示,如果AB=A′B′,BC=B′C′,AC=A′C′,则下列结论正确的是( A )
图1
A.△ABC≌△A′B′C′
B.△ABC≌△C′A′B′
C.△ABC≌△B′C′A′
D.这两个三角形不全等
2.下列三角形中,与图2中△ABC全等的是__③__.
3.如图3所示,AD=BC,AC=BD,用三角形全等的判定“SSS”可证明__△ADC__≌__△BCD__或__△ABD__≌__△BAC__.
图3
知识点2.三角形的稳定性
4.[2018春·泉港区期末]如图4,人字梯中间一般会设计一“拉杆”,这样做的道理是( C )
图4
A.两点之间,线段最短
B.垂线段最短
C.三角形具有稳定性
D.两直线平行,内错角相等
知识点3.三角形全等的判定与性质的综合
5.在△ABC和△A1B1C1中,AB=A1B1,BC=B1C1,AC=A1C1,且∠A=110°,∠B=40°,则∠C1=( C )
A.110° B.40° C.30° D.20°
6.如图5所示,在△ABC和△DBC中,已知AB=DB,AC=DC,则下列结论中错误的是( D )
图5
A.△ABC≌△DBC
B.∠A=∠D
C.BC是∠ACD的平分线
D.∠A=∠BCD
7.如图6,在四边形ABCD中,AB=CD,AD=CB,连结AC,求证:∠ACD=∠CAB.
图6
证明:在△ADC与△CBA中,
∴△ADC≌△CBA(SSS),∴∠ACD=∠CAB.
8.雨伞的截面如图7所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭的过程中,∠BAD与∠CAD有何关系?请说明理由.
图7
解:∠BAD=∠CAD.
理由:∵AB=AC,AE=AB,AF=AC,∴AE=AF.
在△AOE和AOF中,
∴△AOE≌△AOF(SSS),
∴∠EAO=∠FAO,即∠BAD=∠CAD.
知识点4.尺规作角平分线
9.[2018春·历城区期末]如图8,作∠AOB的角平分线的作图过程如下,作法:
图8
(1)在OA和OB上,分别截取OD,OE,使OD=OE;
(2)分别以D,E为圆心,大于DE的长为半径作弧,在∠AOB内,两弧交于点C;
(3)作射线OC,OC就是∠AOB的平分线.
用三角形全等判定法则解释其作图原理,最为恰当的是__SSS__.
【易错点】证明两个三角形全等时,对于有公共部分的角或线段,错把不是对应的边或角当成三角形的对应边或对应角.
10.如图9,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,下列结论错误的是( C )
图9
A.△ABE≌△ACD
B.△ABD≌△ACE
C.∠ACE=30°
D.∠1=70°
第2课时 “边角边”与线段的垂直平分线的性质
知识点1.三角形全等的判定(SAS)
1.如图1中全等的三角形是( D )
① ② ③ ④
图1
A.①和② B.②和③ C.②和④ D.①和③
2.如图2所示,在△ABD和△ACE中,AB=AC,AD=AE,要证△ABD≌△ACE,需补充的条件是( C )
A.∠B=∠C B.∠D=∠E
C.∠DAE=∠BAC D.∠CAD=∠DAC
图2 图3
3.如图3,在四边形ABCD中,AB=AD,CB=CD,若连结AC,BD相交于点O,则图中全等三角形共有( C )
A.1对 B.2对 C.3对 D.4对
4.已知:如图4,OA=OB,OC平分∠AOB,求证:△AOC≌△BOC.
图4
证明:∵OC平分∠AOB,
∴∠AOC=∠BOC.
在△AOC和△BOC中,
∴△AOC≌△BOC(SAS).
知识点2.利用“SAS”判定三角形全等证明线段或角相等
5.如图5,在△ABC和△ABD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA,求证:AC=BD.
图5
证明:在△ADB和△BCA中,
∴△ADB≌△BCA(SAS),∴AC=BD.
6.如图6,在△ABC中,已知AB=AC,AD平分∠BAC,点M,N分别在AB,AC边上,AM=2MB,AN=2NC.求证:DM=DN.
图6
证明:∵AM=2MB,∴AM=AB,同理,AN=AC,
又∵AB=AC,∴AM=AN.
∵AD平分∠BAC,
∴∠MAD=∠NAD.
在△AMD和△AND中,
∴△AMD≌△AND,∴DM=DN.
知识点3.利用“SAS”判定三角形全等来解决实际问题
7.如图7所示,有一块三角形镜子,小明不小心将它打破成Ⅰ,Ⅱ两块,现需配成同样大小的一块.为了方便起见,需带上__Ⅰ__块,其理由是__两边及其夹角分别相等的两个三角形全等__.
图7
知识点4.线段的垂直平分线的性质
8.[2017秋·浉河区期末]如图8,DE是△ABC中AC边的垂直平分线,若BC=8,AB=10,则△EBC的周长是( C )
A.13 B.16 C.18 D.20
【解析】 ∵DE是△ABC中AC边的垂直平分线,∴EA=EC,∴△EBC的周长=BC+BE+EC=BC+BE+EA=BC+BA=18.
图8 图9
9.如图9,在△ABC中,AB=AC=20 cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为 35 cm,则BC的长为( C )
A.5 cm B.10 cm
C.15 cm D.17.5 cm
【解析】 ∵△DBC的周长=BC+BD+CD=35 cm,
又∵DE垂直平分AB,
∴AD=BD,∴BC+AD+CD=35 cm,
∵AC=AD+DC=20 cm,∴BC=35-20=15 cm.
【易错点】“SSA”不能判定两个三角形全等.
10.下列条件能够判断△ABC与△A′B′C全等的是( D )
A.∠A=∠A′
B.AB=A′B′,∠B=∠B′,AC=A′C′
C.AB=A′B′,AC=A′C′
D.AB=A′B′,∠A=∠A′,AC=A′C′
【解析】 A.已知条件为一组对应角相等,不符合全等三角形的判定定理,无法证明两个三角形全等,故此选项错误;
B.已知条件为边边角,不符合全等三角形的判定定理,无法证明两个三角形全等,故此选项错误;
C.已知条件为两条边对应相等,不符合全等三角形的判定定理,无法证明两个三角形全等,故此选项错误;
D.由边角边定理可证两个三角形全等,故此选项正确.
第3课时 “角边角”
知识点 三角形全等的判定(ASA)
1.如图1,已知△ABC三条边、三个角,则甲、乙两个三角形中和△ABC全等的图形是( B )
图1
A.甲 B.乙
C.甲和乙都是 D.都不是
2.如图2所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是__ASA__.
图2
3.如图3,∠1=∠2,∠3=∠4,求证:AC=AD.
图3
证明:∵∠3=∠4,∴∠ABC=∠ABD.
在△ABC和△ABD中,
∴△ABC≌△ABD(ASA),∴AC=AD.
4.[2018秋·延庆区期中]如图4,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,且∠B=∠C.求证:△ABE≌△ACD.
图4
证明:在△ABE与△ACD中,
∴△ABE≌△ACD(ASA).
5.[2018秋·金坛区期中]如图5,在△ABC和△ADE中,AB=AD,∠B=∠D,∠1=∠2.求证:△ABC≌△ADE.
图5
证明:∵∠1=∠2,∴∠DAC+∠1=∠2+∠DAC,
∴∠BAC=∠DAE,
在△ABC和△ADE中,
∴△ABC≌△ADE(ASA).
【易错点】错用判定三角形全等的判定方法.
6.已知:如图6,∠AOD=∠BOC,∠A=∠C,O是AC的中点.求证:△AOB≌△COD.
图6
证明:∵∠AOD=∠BOC,
∴∠AOD+∠DOB=∠BOC+∠BOD,
即∠AOB=∠COD,
∵O是AC的中点,∴AO=CO,
在△AOB与△COD中,
∴△AOB≌△COD.
第4课时 “角角边”与角平分线的性质
知识点1.三角形全等的判定(AAS)
1.如图1,AB=AE,∠1=∠2,∠C=∠D.求证:△ABC≌△AED.
图1
证明:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠EAD.
又∵∠C=∠D,AB=AE,∴△ABC≌△AED(AAS).
2.如图2,已知:在△AFD和△CEB中,点A,E,F,C在同一直线上,AE=CF,∠B=∠D,AD∥BC.求证:AD=BC.
图2
证明:∵AE=CF,∴AF=CE.
∵AD∥BC,∴∠A=∠C.
在△AFD和△CEB中,
∴△AFD≌△CEB(AAS),∴AD=BC.
知识点2.三角形全等判定方法的选用
3.如图3,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( A )
A.AC=BD B.∠CAB=∠DBA
C.∠C=∠D D.BC=AD
图3 图4
4.如图4所示,在△ABC中,∠B=∠C,D为BC边的中点,过点D分别向AB,AC作垂线段,则能够说明△BDE≌△CDF的理由是( D )
A.SSS B.SAS C.ASA D.AAS
知识点3.角平分线的性质
5.如图5,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( A )
图5
A.6 B.5 C.4 D.3
6.[2019·辽阳模拟]如图6,BD平分∠ABC,DE⊥BC于点E,AB=7,DE=4,则S△ABD=( C )
A.28 B.21
C.14 D.7
图6 第6题答图
【解析】 如答图,作DH⊥BA于H.
∵BD平分∠ABC,DE⊥BC,DH⊥AB,
∴DH=DE=4,
∴S△ABD=×7×4=14,故选C.
7.如图7,已知BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.
图7
证明:∵BD为∠ABC的平分线,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
∴△ABD≌△CBD(SAS),∴∠ADB=∠CDB,
∵点P在BD上,且PM⊥AD,PN⊥CD,∴PM=PN.
【易错点】对于全等三角形开放性问题,常常不能正确选用判定方法.
8. 如图8,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( D )
图8
A.∠A=∠D B.BC=EF
C.∠ACB=∠F D.AC=DF
【解析】 ∵∠B=∠DEF,AB=DE,
∴添加∠A=∠D,利用ASA可得△ABC≌△DEF;
∴添加BC=EF,利用SAS可得△ABC≌△DEF;
∴添加∠ACB=∠F,利用AAS可得△ABC≌△DEF;
添加AC=DF不能证明△ABC≌△DEF,故选D.
第1课时 “边边边”
知识点1.三角形全等的判定(SSS)
1.如图1所示,如果AB=A′B′,BC=B′C′,AC=A′C′,则下列结论正确的是( )
图1
A.△ABC≌△A′B′C′
B.△ABC≌△C′A′B′
C.△ABC≌△B′C′A′
D.这两个三角形不全等
2.下列三角形中,与图2中△ABC全等的是____.
3.如图3所示,AD=BC,AC=BD,用三角形全等的判定“SSS”可证明__ __≌__ __或____≌__ __.
图3
知识点2.三角形的稳定性
4.[2018春·泉港区期末]如图4,人字梯中间一般会设计一“拉杆”,这样做的道理是( )
图4
A.两点之间,线段最短
B.垂线段最短
C.三角形具有稳定性
D.两直线平行,内错角相等
知识点3.三角形全等的判定与性质的综合
5.在△ABC和△A1B1C1中,AB=A1B1,BC=B1C1,AC=A1C1,且∠A=110°,∠B=40°,则∠C1=( )
A.110° B.40° C.30° D.20°
6.如图5所示,在△ABC和△DBC中,已知AB=DB,AC=DC,则下列结论中错误的是( )
图5
A.△ABC≌△DBC
B.∠A=∠D
C.BC是∠ACD的平分线
D.∠A=∠BCD
7.如图6,在四边形ABCD中,AB=CD,AD=CB,连结AC,求证:∠ACD=∠CAB.
图6
8.雨伞的截面如图7所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭的过程中,∠BAD与∠CAD有何关系?请说明理由.
图7
知识点4.尺规作角平分线
9.[2018春·历城区期末]如图8,作∠AOB的角平分线的作图过程如下,作法:
图8
(1)在OA和OB上,分别截取OD,OE,使OD=OE;
(2)分别以D,E为圆心,大于DE的长为半径作弧,在∠AOB内,两弧交于点C;
(3)作射线OC,OC就是∠AOB的平分线.
用三角形全等判定法则解释其作图原理,最为恰当的是____.
【易错点】证明两个三角形全等时,对于有公共部分的角或线段,错把不是对应的边或角当成三角形的对应边或对应角.
10.如图9,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,下列结论错误的是( )
图9
A.△ABE≌△ACD
B.△ABD≌△ACE
C.∠ACE=30°
D.∠1=70°
第2课时 “边角边”与线段的垂直平分线的性质
知识点1.三角形全等的判定(SAS)
1.如图1中全等的三角形是( )
① ② ③ ④
图1
A.①和② B.②和③ C.②和④ D.①和③
2.如图2所示,在△ABD和△ACE中,AB=AC,AD=AE,要证△ABD≌△ACE,需补充的条件是( )
A.∠B=∠C B.∠D=∠E
C.∠DAE=∠BAC D.∠CAD=∠DAC
图2 图3
3.如图3,在四边形ABCD中,AB=AD,CB=CD,若连结AC,BD相交于点O,则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
4.已知:如图4,OA=OB,OC平分∠AOB,求证:△AOC≌△BOC.
图4
知识点2.利用“SAS”判定三角形全等证明线段或角相等
5.如图5,在△ABC和△ABD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA,求证:AC=BD.
图5
6.如图6,在△ABC中,已知AB=AC,AD平分∠BAC,点M,N分别在AB,AC边上,AM=2MB,AN=2NC.求证:DM=DN.
图6
知识点3.利用“SAS”判定三角形全等来解决实际问题
7.如图7所示,有一块三角形镜子,小明不小心将它打破成Ⅰ,Ⅱ两块,现需配成同样大小的一块.为了方便起见,需带上____块,其理由是__ __.
图7
知识点4.线段的垂直平分线的性质
8.[2017秋·浉河区期末]如图8,DE是△ABC中AC边的垂直平分线,若BC=8,AB=10,则△EBC的周长是( )
A.13 B.16 C.18 D.20
图8 图9
9.如图9,在△ABC中,AB=AC=20 cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为 35 cm,则BC的长为( C )
A.5 cm B.10 cm
C.15 cm D.17.5 cm
【易错点】“SSA”不能判定两个三角形全等.
10.下列条件能够判断△ABC与△A′B′C全等的是( )
A.∠A=∠A′
B.AB=A′B′,∠B=∠B′,AC=A′C′
C.AB=A′B′,AC=A′C′
D.AB=A′B′,∠A=∠A′,AC=A′C′
第3课时 “角边角”
知识点 三角形全等的判定(ASA)
1.如图1,已知△ABC三条边、三个角,则甲、乙两个三角形中和△ABC全等的图形是( )
图1
A.甲 B.乙
C.甲和乙都是 D.都不是
2.如图2所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是__ __.
图2
3.如图3,∠1=∠2,∠3=∠4,求证:AC=AD.
图3
4.[2018秋·延庆区期中]如图4,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,且∠B=∠C.求证:△ABE≌△ACD.
图4
5.[2018秋·金坛区期中]如图5,在△ABC和△ADE中,AB=AD,∠B=∠D,∠1=∠2.求证:△ABC≌△ADE.
图5
【易错点】错用判定三角形全等的判定方法.
6.已知:如图6,∠AOD=∠BOC,∠A=∠C,O是AC的中点.求证:△AOB≌△COD.
图6
第4课时 “角角边”与角平分线的性质
知识点1.三角形全等的判定(AAS)
1.如图1,AB=AE,∠1=∠2,∠C=∠D.求证:△ABC≌△AED.
图1
2.如图2,已知:在△AFD和△CEB中,点A,E,F,C在同一直线上,AE=CF,∠B=∠D,AD∥BC.求证:AD=BC.
图2
知识点2.三角形全等判定方法的选用
3.如图3,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
A.AC=BD B.∠CAB=∠DBA
C.∠C=∠D D.BC=AD
图3 图4
4.如图4所示,在△ABC中,∠B=∠C,D为BC边的中点,过点D分别向AB,AC作垂线段,则能够说明△BDE≌△CDF的理由是( )
A.SSS B.SAS C.ASA D.AAS
知识点3.角平分线的性质
5.如图5,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
图5
A.6 B.5 C.4 D.3
6.[2019·辽阳模拟]如图6,BD平分∠ABC,DE⊥BC于点E,AB=7,DE=4,则S△ABD=( )
A.28 B.21
C.14 D.7
图6
7.如图7,已知BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.
图7
【易错点】对于全等三角形开放性问题,常常不能正确选用判定方法.
8. 如图8,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
图8
A.∠A=∠D B.BC=EF
C.∠ACB=∠F D.AC=DF
答案
第1课时 “边边边”
知识点1.三角形全等的判定(SSS)
1.如图1所示,如果AB=A′B′,BC=B′C′,AC=A′C′,则下列结论正确的是( A )
图1
A.△ABC≌△A′B′C′
B.△ABC≌△C′A′B′
C.△ABC≌△B′C′A′
D.这两个三角形不全等
2.下列三角形中,与图2中△ABC全等的是__③__.
3.如图3所示,AD=BC,AC=BD,用三角形全等的判定“SSS”可证明__△ADC__≌__△BCD__或__△ABD__≌__△BAC__.
图3
知识点2.三角形的稳定性
4.[2018春·泉港区期末]如图4,人字梯中间一般会设计一“拉杆”,这样做的道理是( C )
图4
A.两点之间,线段最短
B.垂线段最短
C.三角形具有稳定性
D.两直线平行,内错角相等
知识点3.三角形全等的判定与性质的综合
5.在△ABC和△A1B1C1中,AB=A1B1,BC=B1C1,AC=A1C1,且∠A=110°,∠B=40°,则∠C1=( C )
A.110° B.40° C.30° D.20°
6.如图5所示,在△ABC和△DBC中,已知AB=DB,AC=DC,则下列结论中错误的是( D )
图5
A.△ABC≌△DBC
B.∠A=∠D
C.BC是∠ACD的平分线
D.∠A=∠BCD
7.如图6,在四边形ABCD中,AB=CD,AD=CB,连结AC,求证:∠ACD=∠CAB.
图6
证明:在△ADC与△CBA中,
∴△ADC≌△CBA(SSS),∴∠ACD=∠CAB.
8.雨伞的截面如图7所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭的过程中,∠BAD与∠CAD有何关系?请说明理由.
图7
解:∠BAD=∠CAD.
理由:∵AB=AC,AE=AB,AF=AC,∴AE=AF.
在△AOE和AOF中,
∴△AOE≌△AOF(SSS),
∴∠EAO=∠FAO,即∠BAD=∠CAD.
知识点4.尺规作角平分线
9.[2018春·历城区期末]如图8,作∠AOB的角平分线的作图过程如下,作法:
图8
(1)在OA和OB上,分别截取OD,OE,使OD=OE;
(2)分别以D,E为圆心,大于DE的长为半径作弧,在∠AOB内,两弧交于点C;
(3)作射线OC,OC就是∠AOB的平分线.
用三角形全等判定法则解释其作图原理,最为恰当的是__SSS__.
【易错点】证明两个三角形全等时,对于有公共部分的角或线段,错把不是对应的边或角当成三角形的对应边或对应角.
10.如图9,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,下列结论错误的是( C )
图9
A.△ABE≌△ACD
B.△ABD≌△ACE
C.∠ACE=30°
D.∠1=70°
第2课时 “边角边”与线段的垂直平分线的性质
知识点1.三角形全等的判定(SAS)
1.如图1中全等的三角形是( D )
① ② ③ ④
图1
A.①和② B.②和③ C.②和④ D.①和③
2.如图2所示,在△ABD和△ACE中,AB=AC,AD=AE,要证△ABD≌△ACE,需补充的条件是( C )
A.∠B=∠C B.∠D=∠E
C.∠DAE=∠BAC D.∠CAD=∠DAC
图2 图3
3.如图3,在四边形ABCD中,AB=AD,CB=CD,若连结AC,BD相交于点O,则图中全等三角形共有( C )
A.1对 B.2对 C.3对 D.4对
4.已知:如图4,OA=OB,OC平分∠AOB,求证:△AOC≌△BOC.
图4
证明:∵OC平分∠AOB,
∴∠AOC=∠BOC.
在△AOC和△BOC中,
∴△AOC≌△BOC(SAS).
知识点2.利用“SAS”判定三角形全等证明线段或角相等
5.如图5,在△ABC和△ABD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA,求证:AC=BD.
图5
证明:在△ADB和△BCA中,
∴△ADB≌△BCA(SAS),∴AC=BD.
6.如图6,在△ABC中,已知AB=AC,AD平分∠BAC,点M,N分别在AB,AC边上,AM=2MB,AN=2NC.求证:DM=DN.
图6
证明:∵AM=2MB,∴AM=AB,同理,AN=AC,
又∵AB=AC,∴AM=AN.
∵AD平分∠BAC,
∴∠MAD=∠NAD.
在△AMD和△AND中,
∴△AMD≌△AND,∴DM=DN.
知识点3.利用“SAS”判定三角形全等来解决实际问题
7.如图7所示,有一块三角形镜子,小明不小心将它打破成Ⅰ,Ⅱ两块,现需配成同样大小的一块.为了方便起见,需带上__Ⅰ__块,其理由是__两边及其夹角分别相等的两个三角形全等__.
图7
知识点4.线段的垂直平分线的性质
8.[2017秋·浉河区期末]如图8,DE是△ABC中AC边的垂直平分线,若BC=8,AB=10,则△EBC的周长是( C )
A.13 B.16 C.18 D.20
【解析】 ∵DE是△ABC中AC边的垂直平分线,∴EA=EC,∴△EBC的周长=BC+BE+EC=BC+BE+EA=BC+BA=18.
图8 图9
9.如图9,在△ABC中,AB=AC=20 cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为 35 cm,则BC的长为( C )
A.5 cm B.10 cm
C.15 cm D.17.5 cm
【解析】 ∵△DBC的周长=BC+BD+CD=35 cm,
又∵DE垂直平分AB,
∴AD=BD,∴BC+AD+CD=35 cm,
∵AC=AD+DC=20 cm,∴BC=35-20=15 cm.
【易错点】“SSA”不能判定两个三角形全等.
10.下列条件能够判断△ABC与△A′B′C全等的是( D )
A.∠A=∠A′
B.AB=A′B′,∠B=∠B′,AC=A′C′
C.AB=A′B′,AC=A′C′
D.AB=A′B′,∠A=∠A′,AC=A′C′
【解析】 A.已知条件为一组对应角相等,不符合全等三角形的判定定理,无法证明两个三角形全等,故此选项错误;
B.已知条件为边边角,不符合全等三角形的判定定理,无法证明两个三角形全等,故此选项错误;
C.已知条件为两条边对应相等,不符合全等三角形的判定定理,无法证明两个三角形全等,故此选项错误;
D.由边角边定理可证两个三角形全等,故此选项正确.
第3课时 “角边角”
知识点 三角形全等的判定(ASA)
1.如图1,已知△ABC三条边、三个角,则甲、乙两个三角形中和△ABC全等的图形是( B )
图1
A.甲 B.乙
C.甲和乙都是 D.都不是
2.如图2所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是__ASA__.
图2
3.如图3,∠1=∠2,∠3=∠4,求证:AC=AD.
图3
证明:∵∠3=∠4,∴∠ABC=∠ABD.
在△ABC和△ABD中,
∴△ABC≌△ABD(ASA),∴AC=AD.
4.[2018秋·延庆区期中]如图4,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,且∠B=∠C.求证:△ABE≌△ACD.
图4
证明:在△ABE与△ACD中,
∴△ABE≌△ACD(ASA).
5.[2018秋·金坛区期中]如图5,在△ABC和△ADE中,AB=AD,∠B=∠D,∠1=∠2.求证:△ABC≌△ADE.
图5
证明:∵∠1=∠2,∴∠DAC+∠1=∠2+∠DAC,
∴∠BAC=∠DAE,
在△ABC和△ADE中,
∴△ABC≌△ADE(ASA).
【易错点】错用判定三角形全等的判定方法.
6.已知:如图6,∠AOD=∠BOC,∠A=∠C,O是AC的中点.求证:△AOB≌△COD.
图6
证明:∵∠AOD=∠BOC,
∴∠AOD+∠DOB=∠BOC+∠BOD,
即∠AOB=∠COD,
∵O是AC的中点,∴AO=CO,
在△AOB与△COD中,
∴△AOB≌△COD.
第4课时 “角角边”与角平分线的性质
知识点1.三角形全等的判定(AAS)
1.如图1,AB=AE,∠1=∠2,∠C=∠D.求证:△ABC≌△AED.
图1
证明:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠EAD.
又∵∠C=∠D,AB=AE,∴△ABC≌△AED(AAS).
2.如图2,已知:在△AFD和△CEB中,点A,E,F,C在同一直线上,AE=CF,∠B=∠D,AD∥BC.求证:AD=BC.
图2
证明:∵AE=CF,∴AF=CE.
∵AD∥BC,∴∠A=∠C.
在△AFD和△CEB中,
∴△AFD≌△CEB(AAS),∴AD=BC.
知识点2.三角形全等判定方法的选用
3.如图3,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( A )
A.AC=BD B.∠CAB=∠DBA
C.∠C=∠D D.BC=AD
图3 图4
4.如图4所示,在△ABC中,∠B=∠C,D为BC边的中点,过点D分别向AB,AC作垂线段,则能够说明△BDE≌△CDF的理由是( D )
A.SSS B.SAS C.ASA D.AAS
知识点3.角平分线的性质
5.如图5,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( A )
图5
A.6 B.5 C.4 D.3
6.[2019·辽阳模拟]如图6,BD平分∠ABC,DE⊥BC于点E,AB=7,DE=4,则S△ABD=( C )
A.28 B.21
C.14 D.7
图6 第6题答图
【解析】 如答图,作DH⊥BA于H.
∵BD平分∠ABC,DE⊥BC,DH⊥AB,
∴DH=DE=4,
∴S△ABD=×7×4=14,故选C.
7.如图7,已知BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.
图7
证明:∵BD为∠ABC的平分线,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
∴△ABD≌△CBD(SAS),∴∠ADB=∠CDB,
∵点P在BD上,且PM⊥AD,PN⊥CD,∴PM=PN.
【易错点】对于全等三角形开放性问题,常常不能正确选用判定方法.
8. 如图8,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( D )
图8
A.∠A=∠D B.BC=EF
C.∠ACB=∠F D.AC=DF
【解析】 ∵∠B=∠DEF,AB=DE,
∴添加∠A=∠D,利用ASA可得△ABC≌△DEF;
∴添加BC=EF,利用SAS可得△ABC≌△DEF;
∴添加∠ACB=∠F,利用AAS可得△ABC≌△DEF;
添加AC=DF不能证明△ABC≌△DEF,故选D.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
