浙教版数学八上第1章三角形的初步知识单元巩固验收卷(含答案)
文档属性
| 名称 | 浙教版数学八上第1章三角形的初步知识单元巩固验收卷(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 161.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-20 00:00:00 | ||
图片预览



文档简介
第1章单元巩固验收卷
(时间:90分钟 满分:100分)
一、选择题(本题共有10小题,每小题3分,共30分)
1.[金华校级期中改编]下列命题中,正确的是( )
A.三角形的一个外角大于任何一个内角
B.三角形的一条中线将三角形分成两个面积相等的三角形
C.两边和其中一边的对角分别相等的两个三角形全等
D.三角形的高线、中线、角平分线都在三角形内部
2.[杭州富阳区期末]以下列长度的线段为边,能组成三角形的是( )
A.1 cm,2 cm,3 cm B.15 cm,8 cm,6 cm
C.10 cm,4 cm,7 cm D.3 cm,3 cm,7 cm
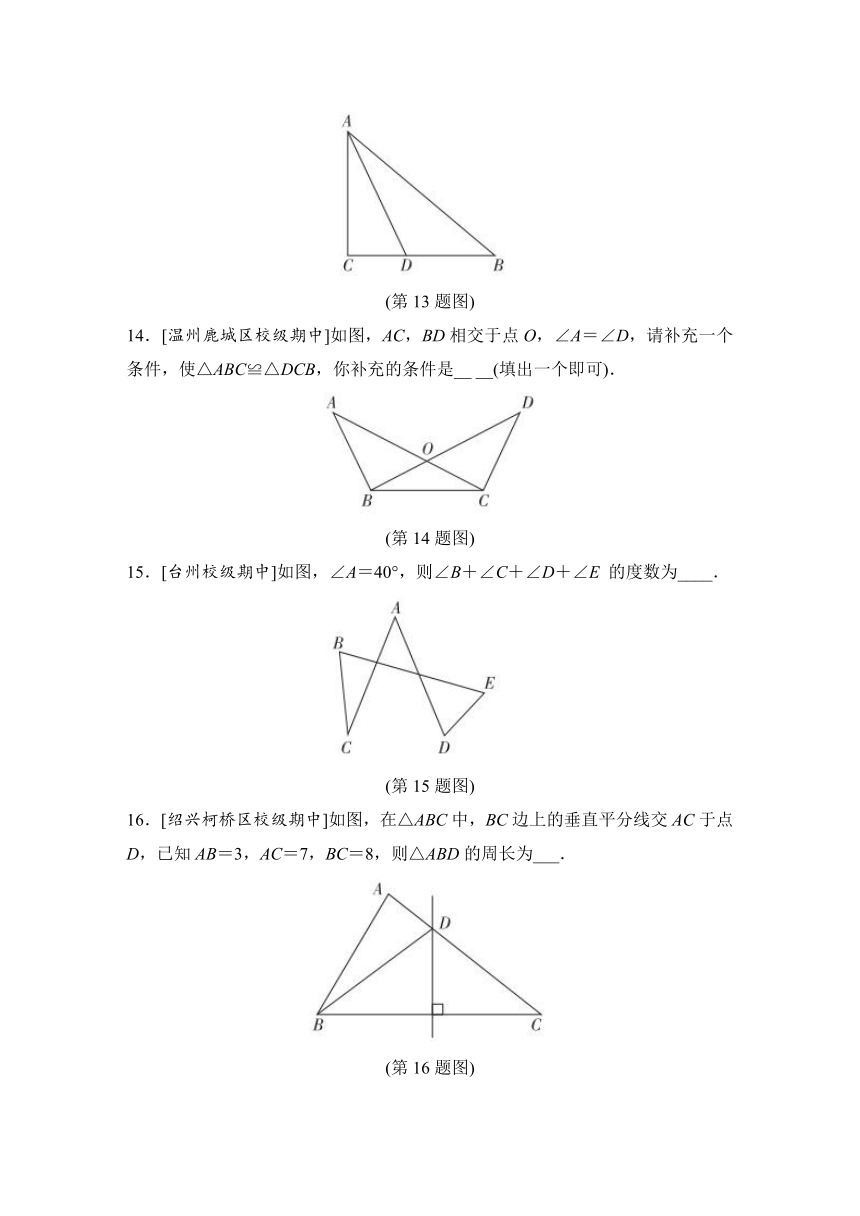
3.[宁波江北区校级期末]如图,在△ABC中,∠A=35°,∠C=45°,则与∠ABC相邻的外角的度数是( )
A.35° B.45° C.80° D.100°
(第3题图) (第4题图)
4.[杭州上城区校级期中]如图,△ABC中,∠A=50°,点E,F在AB,AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于( )
A.130° B.120° C.65° D.100°
5.[金华校级期中]如图,在下列条件中,不能证明△ABD≌△ACD的是( )
(第5题图)
A.BD=DC,AB=AC
B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD
D.∠B=∠C,BD=DC
6.[杭州上城区校级期中]下列各组所列条件中,不能判断△ABC和△DEF全等的是( )
A.∠B=∠E,∠A=∠F,AC=DE
B.AB=EF,∠B=∠F,∠A=∠E
C.AB=DF,∠C=∠E,∠B=∠F
D.BC=DE,AC=DF,∠C=∠D
7.[金华校级期中]如图,直线MN是线段AB的垂直平分线,交BC于点D,连结AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )
(第7题图)
A.20 B.17 C.14 D.7
8.[杭州萧山区期末]给出下列命题:①两边及其中一边上的中线对应相等的两个三角形全等;②底边和顶角对应相等的两个等腰三角形全等;③斜边和斜边上的高线对应相等的两个直角三角形全等.其中属于真命题的是( D )
A.①② B.②③ C.①③ D.①②③
9.[湖州校级期中]如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF-S△BEF=( )
(第9题图)
A.1 B.2 C.3 D.4
10.[杭州西湖区校级期中]如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于点G.若∠BDC=140°,∠BGC=110°,则∠A的度数为( )
A.70° B.80° C.50° D.55°
(第10题图)
二、填空题(本题共有6小题,每小题3分,共18分)
11.[绍兴柯桥区校级期中]已知△ABC的面积为6,AD是△ABC的中线,则△ABD的面积为____.
12.[宁波海曙区校级期末改编]若1,8,x是一个三角形的三边,则x的值可能是____.(填写一个即可)
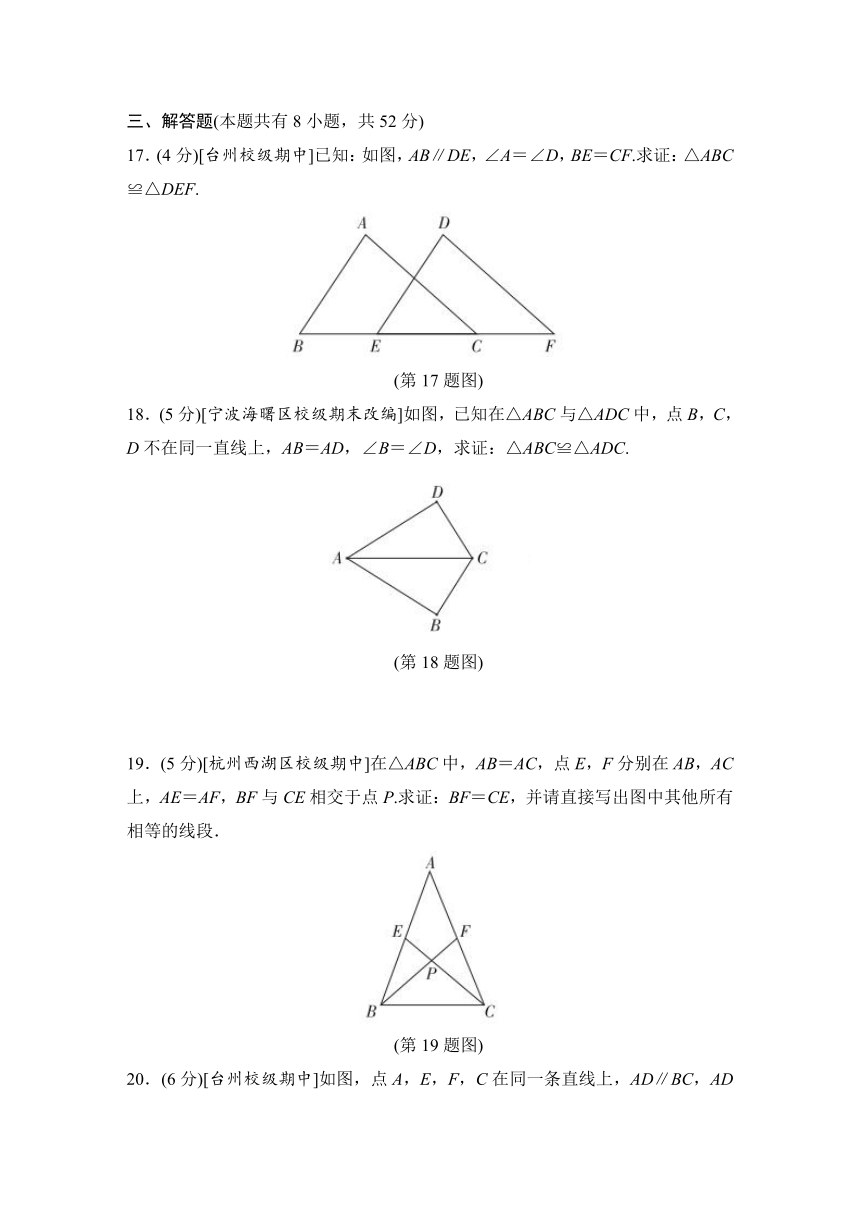
13.[宁波海曙区校级期末]如图,△ABC中,∠C=90°,点D是BC上一点,连结AD.若CD=3,∠B=40°,∠CAD=25°,则点D到AB的距离为____.
(第13题图)
14.[温州鹿城区校级期中]如图,AC,BD相交于点O,∠A=∠D,请补充一个条件,使△ABC≌△DCB,你补充的条件是__ __(填出一个即可).
(第14题图)
15.[台州校级期中]如图,∠A=40°,则∠B+∠C+∠D+∠E 的度数为____.
(第15题图)
16.[绍兴柯桥区校级期中]如图,在△ABC中,BC边上的垂直平分线交AC于点D,已知AB=3,AC=7,BC=8,则△ABD的周长为___.
(第16题图)
三、解答题(本题共有8小题,共52分)
17.(4分)[台州校级期中]已知:如图,AB∥DE,∠A=∠D,BE=CF.求证:△ABC≌△DEF.
(第17题图)
18.(5分)[宁波海曙区校级期末改编]如图,已知在△ABC与△ADC中,点B,C,D不在同一直线上,AB=AD,∠B=∠D,求证:△ABC≌△ADC.
(第18题图)
19.(5分)[杭州西湖区校级期中]在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:BF=CE,并请直接写出图中其他所有相等的线段.
(第19题图)
20.(6分)[台州校级期中]如图,点A,E,F,C在同一条直线上,AD∥BC,AD=CB,AE=CF.求证:BE=DF.
(第20题图)
21.(6分)[温州校级期末]已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC.求证:BC=DE.
(第21题图)
22.(8分)[乐清校级期中]如图,△ABC的两条高线AD,BE相交于点H,且AD=BD,求证:△BDH≌△ADC.
(第22题图)
23.(8分)[杭州西湖区校级期中]如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为点H.求证:
(第23题图)
(1)∠BGC=90°+∠BAC;
(2)∠1=∠2.
24.(10分)[绍兴柯桥区校级期中]如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
(1)若固定三根木条AB,BC,AD不动,AB=AD=2 cm,BC=5 cm,如图,量得第四根木条CD=5 cm,判断此时∠B与∠D是否相等,并说明理由;
(2)若固定一根木条AB不动,AB=2 cm,量得木条CD=5 cm,如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A,C,D能构成周长为30 cm的三角形,求出木条AD,BC的长度.
(第24题图)
答案
一、选择题(本题共有10小题,每小题3分,共30分)
1.[金华校级期中改编]下列命题中,正确的是( B )
A.三角形的一个外角大于任何一个内角
B.三角形的一条中线将三角形分成两个面积相等的三角形
C.两边和其中一边的对角分别相等的两个三角形全等
D.三角形的高线、中线、角平分线都在三角形内部
2.[杭州富阳区期末]以下列长度的线段为边,能组成三角形的是( C )
A.1 cm,2 cm,3 cm B.15 cm,8 cm,6 cm
C.10 cm,4 cm,7 cm D.3 cm,3 cm,7 cm
3.[宁波江北区校级期末]如图,在△ABC中,∠A=35°,∠C=45°,则与∠ABC相邻的外角的度数是( C )
A.35° B.45° C.80° D.100°
【解析】 该外角=∠A+∠C=35°+45°=80°.故选C.
(第3题图) (第4题图)
4.[杭州上城区校级期中]如图,△ABC中,∠A=50°,点E,F在AB,AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于( D )
A.130° B.120° C.65° D.100°
【解析】 设∠AEF=x,∠AFE=y,则∠DEF=x,∠DFE=y,
∴2x+∠1+2y+∠2=360°,
∵x+y=130°,
∴∠1+∠2=100°.故选D.
5.[金华校级期中]如图,在下列条件中,不能证明△ABD≌△ACD的是( D )
(第5题图)
A.BD=DC,AB=AC
B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD
D.∠B=∠C,BD=DC
【解析】 A,B,C分别根据SSS,SAS,AAS可证明全等.故选D.
6.[杭州上城区校级期中]下列各组所列条件中,不能判断△ABC和△DEF全等的是( A )
A.∠B=∠E,∠A=∠F,AC=DE
B.AB=EF,∠B=∠F,∠A=∠E
C.AB=DF,∠C=∠E,∠B=∠F
D.BC=DE,AC=DF,∠C=∠D
【解析】 选项A,不符合全等三角形的判定定理,错误;选项B,符合ASA,正确;选项C,符合AAS,正确;选项D,符合SAS,正确.故选A.
7.[金华校级期中]如图,直线MN是线段AB的垂直平分线,交BC于点D,连结AD.若△ADC的周长为10,AB=7,则△ABC的周长为( B )
(第7题图)
A.20 B.17 C.14 D.7
【解析】 ∵MN是AB的垂直平分线,
∴AD=BD,∵△ADC的周长为10,
∴AD+CD+AC=BD+DC+AC=10,
∴AC+BC=10,∵AB=7,
∴△ABC的周长为AB+AC+BC=7+10=17,
故选B.
8.[杭州萧山区期末]给出下列命题:①两边及其中一边上的中线对应相等的两个三角形全等;②底边和顶角对应相等的两个等腰三角形全等;③斜边和斜边上的高线对应相等的两个直角三角形全等.其中属于真命题的是( D )
A.①② B.②③ C.①③ D.①②③
9.[湖州校级期中]如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF-S△BEF=( B )
(第9题图)
A.1 B.2 C.3 D.4
【解析】 ∵S△ABC=12,EC=2BE,点D是AC的中点,
∴S△ABE=×12=4,S△ABD=×12=6,
∴S△ABD-S△ABE=S△ADF-S△BEF=2.故选B.
10.[杭州西湖区校级期中]如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于点G.若∠BDC=140°,∠BGC=110°,则∠A的度数为( B )
A.70° B.80° C.50° D.55°
(第10题图) 第10题答图
【解析】 如答图,连结BC.
∵∠BDC=140°,
∴∠DBC+∠DCB=180°-140°=40°.
∵∠BGC=110°,
∴∠GBC+∠GCB=180°-110°=70°.
∵BF是∠ABD的平分线,CE是∠ACD的平分线,
∴∠GBD+∠GCD=∠ABD+∠ACD=70°-40°=30°,
∴∠ABC+∠ACB=30°×2+40°=100°,
∴∠A=180°-100°=80°.故选B.
二、填空题(本题共有6小题,每小题3分,共18分)
11.[绍兴柯桥区校级期中]已知△ABC的面积为6,AD是△ABC的中线,则△ABD的面积为__3__.
【解析】 ∵△ABC的面积为6,AD是△ABC的中线,
∴△ABD的面积=×6=3.
12.[宁波海曙区校级期末改编]若1,8,x是一个三角形的三边,则x的值可能是__8(x满足7【解析】 根据“三角形的两边之和大于第三边,两边之差小于第三边”,可知8-1<x<8+1,即7<x<9.
13.[宁波海曙区校级期末]如图,△ABC中,∠C=90°,点D是BC上一点,连结AD.若CD=3,∠B=40°,∠CAD=25°,则点D到AB的距离为__3__.
(第13题图) 第13题答图
【解析】 作DE⊥AB,垂足为E,如答图所示,
∵∠B=40°,∴∠BAC=50°,
∵∠CAD=25°,
∴AD是∠BAC的平分线.
∴DE=CD=3,
即点D到AB的距离为3.
14.[温州鹿城区校级期中]如图,AC,BD相交于点O,∠A=∠D,请补充一个条件,使△ABC≌△DCB,你补充的条件是__∠ABC=∠DCB__(填出一个即可).
(第14题图)
【解析】 已知△ABC和△DCB中,有一组对应边相等(BC=CB),一组对应角相等(∠A=∠D),需再添加一组对应角,即可利用AAS证明△ABC≌△DCB,即可添加条件∠ABC=∠DCB或∠ACB=∠DBC.答案不唯一,符合要求即可.
15.[台州校级期中]如图,∠A=40°,则∠B+∠C+∠D+∠E 的度数为__220°__.
(第15题图) 第15题答图
【解析】 如答图,∵∠A=40°,
∴∠2+∠1=140°,
∵∠1=∠3=180°-(∠B+∠C),∠2=∠4=180°-(∠D+∠E),
∴∠B+∠C+∠D+∠E=360°-∠3-∠4=220°.
16.[绍兴柯桥区校级期中]如图,在△ABC中,BC边上的垂直平分线交AC于点D,已知AB=3,AC=7,BC=8,则△ABD的周长为__10__.
(第16题图)
【解析】 ∵BC边上的垂直平分线交AC于点D,
∴BD=CD.
∴△ABD的周长=AB+AD+BD=AB+(AD+CD)=AB+AC=3+7=10.
三、解答题(本题共有8小题,共52分)
17.(4分)[台州校级期中]已知:如图,AB∥DE,∠A=∠D,BE=CF.求证:△ABC≌△DEF.
(第17题图)
证明:∵BE=CF,∴BC=EF,
∵AB∥DE,∴∠B=∠DEF,
∵∠A=∠D,∴△ABC≌△DEF.
18.(5分)[宁波海曙区校级期末改编]如图,已知在△ABC与△ADC中,点B,C,D不在同一直线上,AB=AD,∠B=∠D,求证:△ABC≌△ADC.
(第18题图) 第18题答图
解:如答图,连结BD.
∵AB=AD,∴∠ADB=∠ABD,
∵∠ABC=∠ADC,∴∠CBD=∠CDB,
∴BC=DC,
在△ABC和△ADC中,
∴△ABC≌△ADC.
19.(5分)[杭州西湖区校级期中]在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:BF=CE,并请直接写出图中其他所有相等的线段.
(第19题图)
证明:在△ABF和△ACE中,
∴△ABF≌△ACE(SAS),
∴BF=CE,
其他所有相等的线段有:BE=CF,BP=CP,PE=PF.
20.(6分)[台州校级期中]如图,点A,E,F,C在同一条直线上,AD∥BC,AD=CB,AE=CF.求证:BE=DF.
(第20题图)
证明:∵AD∥BC,∴∠A=∠C,
∵AE=CF,∴AE+EF=CF+EF,即AF=CE,
在△ADF和△CBE中,
∴△ADF≌△CBE(SAS),∴BE=DF.
21.(6分)[温州校级期末]已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC.求证:BC=DE.
(第21题图)
证明:∵AB∥EC,
∴∠A=∠ACE,
在△ABC和△CDE中,
∵∠B=∠EDC,∠A=∠ACE,AC=CE,
∴△ABC≌△CDE(AAS),
∴BC=DE.
22.(8分)[乐清校级期中]如图,△ABC的两条高线AD,BE相交于点H,且AD=BD,求证:△BDH≌△ADC.
(第22题图)
解:∵∠BDH=∠CEB=90°,
∴∠DBH+∠BHD=∠DBH+∠C=90°,∴∠BHD=∠C,
在△BDH和△ADC中,
∵∠BDH=∠ADC,∠BHD=∠C,BD=AD,∴△BDH≌△ADC.
23.(8分)[杭州西湖区校级期中]如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为点H.求证:
(第23题图)
(1)∠BGC=90°+∠BAC;
(2)∠1=∠2.
证明:(1)由三角形内角和定理可知:∠ABC+∠ACB=180°-∠BAC.
∵BG,CG分别平分∠ABC,∠ACB,
∴∠GBC=∠ABC,∠GCB=∠ACB,
∴∠GBC+∠GCB=(∠ABC+∠ACB)
=(180°-∠BAC)=90°-∠BAC,
∴∠BGC=180°-(∠GBC+∠GCB)
=90°+∠BAC;
(2)∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∴∠1=∠BAD+∠ABG.
∵GH⊥BC,∴∠GHC=90°,
∴∠2=90°-∠GCH=90°-∠ACB
=90°-(180°-∠BAC-∠ABC)
=∠BAD+∠ABG.∴∠1=∠2.
24.(10分)[绍兴柯桥区校级期中]如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
(1)若固定三根木条AB,BC,AD不动,AB=AD=2 cm,BC=5 cm,如图,量得第四根木条CD=5 cm,判断此时∠B与∠D是否相等,并说明理由;
(2)若固定一根木条AB不动,AB=2 cm,量得木条CD=5 cm,如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A,C,D能构成周长为30 cm的三角形,求出木条AD,BC的长度.
(第24题图) 第24题答图
解:(1)相等.
理由:如答图,连结AC,
在△ACD和△ACB中,
∴△ACD≌△ACB,∴∠B=∠D;
(2)设AD=x,BC=y,
当点C在点D右侧时,
解得
当点C在点D左侧时,
解得
此时AC=17,CD=5,AD=8,5+8<17,不合题意,
∴AD=13 cm,BC=10 cm.
(时间:90分钟 满分:100分)
一、选择题(本题共有10小题,每小题3分,共30分)
1.[金华校级期中改编]下列命题中,正确的是( )
A.三角形的一个外角大于任何一个内角
B.三角形的一条中线将三角形分成两个面积相等的三角形
C.两边和其中一边的对角分别相等的两个三角形全等
D.三角形的高线、中线、角平分线都在三角形内部
2.[杭州富阳区期末]以下列长度的线段为边,能组成三角形的是( )
A.1 cm,2 cm,3 cm B.15 cm,8 cm,6 cm
C.10 cm,4 cm,7 cm D.3 cm,3 cm,7 cm
3.[宁波江北区校级期末]如图,在△ABC中,∠A=35°,∠C=45°,则与∠ABC相邻的外角的度数是( )
A.35° B.45° C.80° D.100°
(第3题图) (第4题图)
4.[杭州上城区校级期中]如图,△ABC中,∠A=50°,点E,F在AB,AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于( )
A.130° B.120° C.65° D.100°
5.[金华校级期中]如图,在下列条件中,不能证明△ABD≌△ACD的是( )
(第5题图)
A.BD=DC,AB=AC
B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD
D.∠B=∠C,BD=DC
6.[杭州上城区校级期中]下列各组所列条件中,不能判断△ABC和△DEF全等的是( )
A.∠B=∠E,∠A=∠F,AC=DE
B.AB=EF,∠B=∠F,∠A=∠E
C.AB=DF,∠C=∠E,∠B=∠F
D.BC=DE,AC=DF,∠C=∠D
7.[金华校级期中]如图,直线MN是线段AB的垂直平分线,交BC于点D,连结AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )
(第7题图)
A.20 B.17 C.14 D.7
8.[杭州萧山区期末]给出下列命题:①两边及其中一边上的中线对应相等的两个三角形全等;②底边和顶角对应相等的两个等腰三角形全等;③斜边和斜边上的高线对应相等的两个直角三角形全等.其中属于真命题的是( D )
A.①② B.②③ C.①③ D.①②③
9.[湖州校级期中]如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF-S△BEF=( )
(第9题图)
A.1 B.2 C.3 D.4
10.[杭州西湖区校级期中]如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于点G.若∠BDC=140°,∠BGC=110°,则∠A的度数为( )
A.70° B.80° C.50° D.55°
(第10题图)
二、填空题(本题共有6小题,每小题3分,共18分)
11.[绍兴柯桥区校级期中]已知△ABC的面积为6,AD是△ABC的中线,则△ABD的面积为____.
12.[宁波海曙区校级期末改编]若1,8,x是一个三角形的三边,则x的值可能是____.(填写一个即可)
13.[宁波海曙区校级期末]如图,△ABC中,∠C=90°,点D是BC上一点,连结AD.若CD=3,∠B=40°,∠CAD=25°,则点D到AB的距离为____.
(第13题图)
14.[温州鹿城区校级期中]如图,AC,BD相交于点O,∠A=∠D,请补充一个条件,使△ABC≌△DCB,你补充的条件是__ __(填出一个即可).
(第14题图)
15.[台州校级期中]如图,∠A=40°,则∠B+∠C+∠D+∠E 的度数为____.
(第15题图)
16.[绍兴柯桥区校级期中]如图,在△ABC中,BC边上的垂直平分线交AC于点D,已知AB=3,AC=7,BC=8,则△ABD的周长为___.
(第16题图)
三、解答题(本题共有8小题,共52分)
17.(4分)[台州校级期中]已知:如图,AB∥DE,∠A=∠D,BE=CF.求证:△ABC≌△DEF.
(第17题图)
18.(5分)[宁波海曙区校级期末改编]如图,已知在△ABC与△ADC中,点B,C,D不在同一直线上,AB=AD,∠B=∠D,求证:△ABC≌△ADC.
(第18题图)
19.(5分)[杭州西湖区校级期中]在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:BF=CE,并请直接写出图中其他所有相等的线段.
(第19题图)
20.(6分)[台州校级期中]如图,点A,E,F,C在同一条直线上,AD∥BC,AD=CB,AE=CF.求证:BE=DF.
(第20题图)
21.(6分)[温州校级期末]已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC.求证:BC=DE.
(第21题图)
22.(8分)[乐清校级期中]如图,△ABC的两条高线AD,BE相交于点H,且AD=BD,求证:△BDH≌△ADC.
(第22题图)
23.(8分)[杭州西湖区校级期中]如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为点H.求证:
(第23题图)
(1)∠BGC=90°+∠BAC;
(2)∠1=∠2.
24.(10分)[绍兴柯桥区校级期中]如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
(1)若固定三根木条AB,BC,AD不动,AB=AD=2 cm,BC=5 cm,如图,量得第四根木条CD=5 cm,判断此时∠B与∠D是否相等,并说明理由;
(2)若固定一根木条AB不动,AB=2 cm,量得木条CD=5 cm,如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A,C,D能构成周长为30 cm的三角形,求出木条AD,BC的长度.
(第24题图)
答案
一、选择题(本题共有10小题,每小题3分,共30分)
1.[金华校级期中改编]下列命题中,正确的是( B )
A.三角形的一个外角大于任何一个内角
B.三角形的一条中线将三角形分成两个面积相等的三角形
C.两边和其中一边的对角分别相等的两个三角形全等
D.三角形的高线、中线、角平分线都在三角形内部
2.[杭州富阳区期末]以下列长度的线段为边,能组成三角形的是( C )
A.1 cm,2 cm,3 cm B.15 cm,8 cm,6 cm
C.10 cm,4 cm,7 cm D.3 cm,3 cm,7 cm
3.[宁波江北区校级期末]如图,在△ABC中,∠A=35°,∠C=45°,则与∠ABC相邻的外角的度数是( C )
A.35° B.45° C.80° D.100°
【解析】 该外角=∠A+∠C=35°+45°=80°.故选C.
(第3题图) (第4题图)
4.[杭州上城区校级期中]如图,△ABC中,∠A=50°,点E,F在AB,AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于( D )
A.130° B.120° C.65° D.100°
【解析】 设∠AEF=x,∠AFE=y,则∠DEF=x,∠DFE=y,
∴2x+∠1+2y+∠2=360°,
∵x+y=130°,
∴∠1+∠2=100°.故选D.
5.[金华校级期中]如图,在下列条件中,不能证明△ABD≌△ACD的是( D )
(第5题图)
A.BD=DC,AB=AC
B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD
D.∠B=∠C,BD=DC
【解析】 A,B,C分别根据SSS,SAS,AAS可证明全等.故选D.
6.[杭州上城区校级期中]下列各组所列条件中,不能判断△ABC和△DEF全等的是( A )
A.∠B=∠E,∠A=∠F,AC=DE
B.AB=EF,∠B=∠F,∠A=∠E
C.AB=DF,∠C=∠E,∠B=∠F
D.BC=DE,AC=DF,∠C=∠D
【解析】 选项A,不符合全等三角形的判定定理,错误;选项B,符合ASA,正确;选项C,符合AAS,正确;选项D,符合SAS,正确.故选A.
7.[金华校级期中]如图,直线MN是线段AB的垂直平分线,交BC于点D,连结AD.若△ADC的周长为10,AB=7,则△ABC的周长为( B )
(第7题图)
A.20 B.17 C.14 D.7
【解析】 ∵MN是AB的垂直平分线,
∴AD=BD,∵△ADC的周长为10,
∴AD+CD+AC=BD+DC+AC=10,
∴AC+BC=10,∵AB=7,
∴△ABC的周长为AB+AC+BC=7+10=17,
故选B.
8.[杭州萧山区期末]给出下列命题:①两边及其中一边上的中线对应相等的两个三角形全等;②底边和顶角对应相等的两个等腰三角形全等;③斜边和斜边上的高线对应相等的两个直角三角形全等.其中属于真命题的是( D )
A.①② B.②③ C.①③ D.①②③
9.[湖州校级期中]如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF-S△BEF=( B )
(第9题图)
A.1 B.2 C.3 D.4
【解析】 ∵S△ABC=12,EC=2BE,点D是AC的中点,
∴S△ABE=×12=4,S△ABD=×12=6,
∴S△ABD-S△ABE=S△ADF-S△BEF=2.故选B.
10.[杭州西湖区校级期中]如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于点G.若∠BDC=140°,∠BGC=110°,则∠A的度数为( B )
A.70° B.80° C.50° D.55°
(第10题图) 第10题答图
【解析】 如答图,连结BC.
∵∠BDC=140°,
∴∠DBC+∠DCB=180°-140°=40°.
∵∠BGC=110°,
∴∠GBC+∠GCB=180°-110°=70°.
∵BF是∠ABD的平分线,CE是∠ACD的平分线,
∴∠GBD+∠GCD=∠ABD+∠ACD=70°-40°=30°,
∴∠ABC+∠ACB=30°×2+40°=100°,
∴∠A=180°-100°=80°.故选B.
二、填空题(本题共有6小题,每小题3分,共18分)
11.[绍兴柯桥区校级期中]已知△ABC的面积为6,AD是△ABC的中线,则△ABD的面积为__3__.
【解析】 ∵△ABC的面积为6,AD是△ABC的中线,
∴△ABD的面积=×6=3.
12.[宁波海曙区校级期末改编]若1,8,x是一个三角形的三边,则x的值可能是__8(x满足7
13.[宁波海曙区校级期末]如图,△ABC中,∠C=90°,点D是BC上一点,连结AD.若CD=3,∠B=40°,∠CAD=25°,则点D到AB的距离为__3__.
(第13题图) 第13题答图
【解析】 作DE⊥AB,垂足为E,如答图所示,
∵∠B=40°,∴∠BAC=50°,
∵∠CAD=25°,
∴AD是∠BAC的平分线.
∴DE=CD=3,
即点D到AB的距离为3.
14.[温州鹿城区校级期中]如图,AC,BD相交于点O,∠A=∠D,请补充一个条件,使△ABC≌△DCB,你补充的条件是__∠ABC=∠DCB__(填出一个即可).
(第14题图)
【解析】 已知△ABC和△DCB中,有一组对应边相等(BC=CB),一组对应角相等(∠A=∠D),需再添加一组对应角,即可利用AAS证明△ABC≌△DCB,即可添加条件∠ABC=∠DCB或∠ACB=∠DBC.答案不唯一,符合要求即可.
15.[台州校级期中]如图,∠A=40°,则∠B+∠C+∠D+∠E 的度数为__220°__.
(第15题图) 第15题答图
【解析】 如答图,∵∠A=40°,
∴∠2+∠1=140°,
∵∠1=∠3=180°-(∠B+∠C),∠2=∠4=180°-(∠D+∠E),
∴∠B+∠C+∠D+∠E=360°-∠3-∠4=220°.
16.[绍兴柯桥区校级期中]如图,在△ABC中,BC边上的垂直平分线交AC于点D,已知AB=3,AC=7,BC=8,则△ABD的周长为__10__.
(第16题图)
【解析】 ∵BC边上的垂直平分线交AC于点D,
∴BD=CD.
∴△ABD的周长=AB+AD+BD=AB+(AD+CD)=AB+AC=3+7=10.
三、解答题(本题共有8小题,共52分)
17.(4分)[台州校级期中]已知:如图,AB∥DE,∠A=∠D,BE=CF.求证:△ABC≌△DEF.
(第17题图)
证明:∵BE=CF,∴BC=EF,
∵AB∥DE,∴∠B=∠DEF,
∵∠A=∠D,∴△ABC≌△DEF.
18.(5分)[宁波海曙区校级期末改编]如图,已知在△ABC与△ADC中,点B,C,D不在同一直线上,AB=AD,∠B=∠D,求证:△ABC≌△ADC.
(第18题图) 第18题答图
解:如答图,连结BD.
∵AB=AD,∴∠ADB=∠ABD,
∵∠ABC=∠ADC,∴∠CBD=∠CDB,
∴BC=DC,
在△ABC和△ADC中,
∴△ABC≌△ADC.
19.(5分)[杭州西湖区校级期中]在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:BF=CE,并请直接写出图中其他所有相等的线段.
(第19题图)
证明:在△ABF和△ACE中,
∴△ABF≌△ACE(SAS),
∴BF=CE,
其他所有相等的线段有:BE=CF,BP=CP,PE=PF.
20.(6分)[台州校级期中]如图,点A,E,F,C在同一条直线上,AD∥BC,AD=CB,AE=CF.求证:BE=DF.
(第20题图)
证明:∵AD∥BC,∴∠A=∠C,
∵AE=CF,∴AE+EF=CF+EF,即AF=CE,
在△ADF和△CBE中,
∴△ADF≌△CBE(SAS),∴BE=DF.
21.(6分)[温州校级期末]已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC.求证:BC=DE.
(第21题图)
证明:∵AB∥EC,
∴∠A=∠ACE,
在△ABC和△CDE中,
∵∠B=∠EDC,∠A=∠ACE,AC=CE,
∴△ABC≌△CDE(AAS),
∴BC=DE.
22.(8分)[乐清校级期中]如图,△ABC的两条高线AD,BE相交于点H,且AD=BD,求证:△BDH≌△ADC.
(第22题图)
解:∵∠BDH=∠CEB=90°,
∴∠DBH+∠BHD=∠DBH+∠C=90°,∴∠BHD=∠C,
在△BDH和△ADC中,
∵∠BDH=∠ADC,∠BHD=∠C,BD=AD,∴△BDH≌△ADC.
23.(8分)[杭州西湖区校级期中]如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为点H.求证:
(第23题图)
(1)∠BGC=90°+∠BAC;
(2)∠1=∠2.
证明:(1)由三角形内角和定理可知:∠ABC+∠ACB=180°-∠BAC.
∵BG,CG分别平分∠ABC,∠ACB,
∴∠GBC=∠ABC,∠GCB=∠ACB,
∴∠GBC+∠GCB=(∠ABC+∠ACB)
=(180°-∠BAC)=90°-∠BAC,
∴∠BGC=180°-(∠GBC+∠GCB)
=90°+∠BAC;
(2)∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∴∠1=∠BAD+∠ABG.
∵GH⊥BC,∴∠GHC=90°,
∴∠2=90°-∠GCH=90°-∠ACB
=90°-(180°-∠BAC-∠ABC)
=∠BAD+∠ABG.∴∠1=∠2.
24.(10分)[绍兴柯桥区校级期中]如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
(1)若固定三根木条AB,BC,AD不动,AB=AD=2 cm,BC=5 cm,如图,量得第四根木条CD=5 cm,判断此时∠B与∠D是否相等,并说明理由;
(2)若固定一根木条AB不动,AB=2 cm,量得木条CD=5 cm,如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A,C,D能构成周长为30 cm的三角形,求出木条AD,BC的长度.
(第24题图) 第24题答图
解:(1)相等.
理由:如答图,连结AC,
在△ACD和△ACB中,
∴△ACD≌△ACB,∴∠B=∠D;
(2)设AD=x,BC=y,
当点C在点D右侧时,
解得
当点C在点D左侧时,
解得
此时AC=17,CD=5,AD=8,5+8<17,不合题意,
∴AD=13 cm,BC=10 cm.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
