1.1 认识三角形第2课时同步课件

(共20张PPT)
浙教版 八年级上
1.1 认识三角形

（第2课时）
新知导入




A
D
C
B
∠BAD =∠CAD
将△ABC的两边AB、AC重合，得到折痕AD，量一量∠BAD 和∠CAD 有什么关系？
新知讲解

一个三角形有几
条角平分线？
在三角形中，一个内角的角平分线与它的对边相交，这个角的顶点与交点之间的线段叫做三角形的角平分线.
三角形的角平分线的定义：



A
B
C

D
∵ AD是 △ ABC的一条角平分线,
∴ ∠ BAD = ∠ CAD = ∠BAC.
1
2

几何语言：
新知讲解
（1）三角形的角平分线是一条线段；
（2）三角形的角平分线仍具有角平分线的基本性质。
三角形的角平分线与角的平分线有什么区别与联系？
新知讲解
线段中点的定义：
1.点C把线段AB分成相等的两条线段AC
和BC，点C叫做线段AB的中点.

A
B
C
2.若AC=BC，
则点C是线段AB的中点.
3.若C是线段AB的中点，则AC=BC.
（或者AC=BC= AB）
（或者AC=BC= AB）



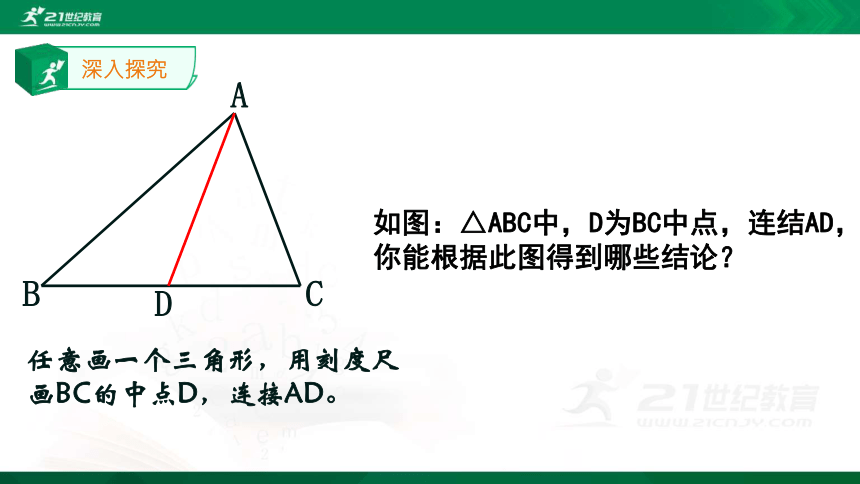
深入探究




D
C
B
任意画一个三角形，用刻度尺
画BC的中点D，连接AD。
A
如图：△ABC中，D为BC中点，连结AD，你能根据此图得到哪些结论？
新知讲解
三角形的中线的定义：
∵AD是△ ABC的 中线，
BD =CD = BC.
1
2

在三角形中，连结一个顶点与它对边 中点的线段,叫做这个三角形的中线.

A
B
C

D


一个三角形
有几条中线？
几何语言：
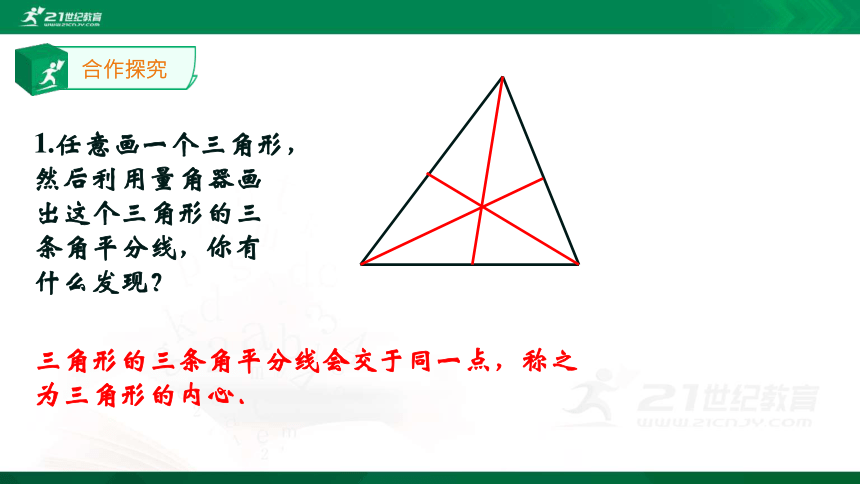
合作探究
1.任意画一个三角形，
然后利用量角器画
出这个三角形的三
条角平分线，你有
什么发现？






三角形的三条角平分线会交于同一点，称之为三角形的内心．
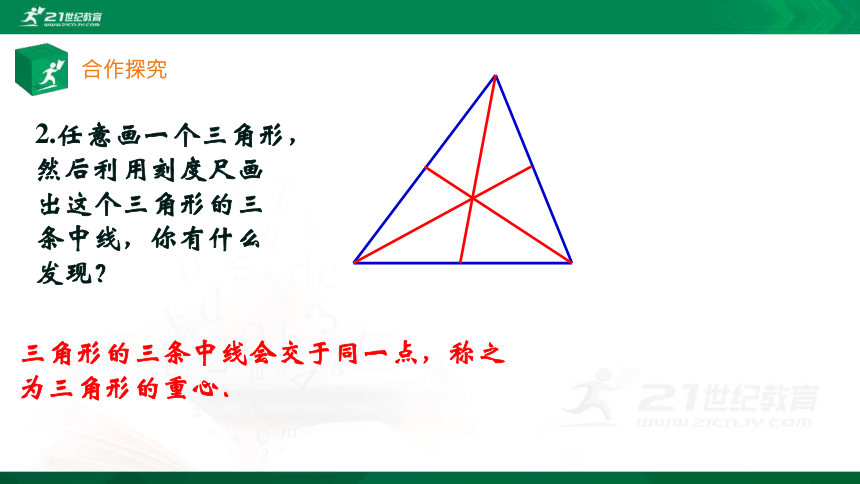
2.任意画一个三角形，
然后利用刻度尺画
出这个三角形的三
条中线，你有什么
发现？






三角形的三条中线会交于同一点，称之为三角形的重心．
合作探究
1、AD是ΔABC的角平分线（左图），那么∠BAC= ∠BAD；
2、AE是ΔABC的中线（右图），那么BC= BE.




A
D
C
B



B
C
E

A
课堂练习
2
2
如图，AF是ΔABC的角平分线，AE是BC边上的中线，选择“＞”“＜”或“=”号填空：




E
C
B
（1）BE___EC
（2）∠CAF___―∠BAC
（3）∠AFB___∠C+∠FAB
（4）∠AEC___∠B
=
=
=
＞

课堂练习
F
A
用三角尺分别作如下锐角三角形ABC,直角三
角形DEF和钝角三角形PQR的各边上的高.
观察你所作的图形,比较三个三角形中三条高的位置,与三角形之间有什么关系?







A
C
B



E
F
D



R
Q
P





合作探究
三角形的高
A
从三角形的一个顶点
B
C
向它的对边


所在直线作垂线，


顶点
和垂足
之间的线段
叫做三角形的高.
如右上图, 线段AD就是BC边上的高.
任意画一个锐角△ABC,请你画出BC边上的高.

注意标明垂直的记号和垂足的字母.
A

B
C
D


合作探究



A
B
C











D
E
F








P
Q
R














3
3
3
都在三角
形内部
直角边上的高分别与另一条直角边重合，还有一条高在三角形内部
夹钝角两边上的高在三角形外部，另一条高在内部
在相应顶点的对边上
①是直角的顶点
②在斜边上
①在相应顶点的对边的延长线上
②在钝角的对边上
在三角形内部
在直角顶点
在三角形外部
高 锐角三角形 直角三角形 钝角三角形
条数
位置

垂足
交点
图形


结论
　　　　　如图，在△ABC中，AD是△ABC的高，AE是△ABC的角平分线。已知∠BAC＝82°，∠C＝40°，求∠DAE的大小。
练习一　





E
D
C
B
A


55°
思路：
①AE是△ABC的角平分线，∠BAC＝82°，得∠BAE=∠CAE=41°
②在△ABE中，∠AEB=180°-55°-41°=84°
③AD是△ABC的高，得∠ADE=90°，即得∠DAE=180°-90°-84°=6°
在△ABC中，AE，AD分别是BC边上的中线和高。说明△ABE的面积与△AEC的面积相等。
解：
∵ AE是BC边上的中线
∴ BE = EC








A
D
E
C
B
S △ABE= BE · AD
S △AEC= EC · AD
∴
S △AEC
S △ABE
=
　　三角形的中线将三角形分成面积相等的两等份
练习二　
中考真题
B
（2019湖北黄冈）如图，直线AB∥CD，直线EC分别与AB，CD相交于点A、点C，AD平分∠BAC，已知∠ACD＝80°，则∠DAC的度数为　 　．
【分析】依据平行线的性质，即可得到∠BAC的度数，再根据角平分线的定义，即可得到∠DAC的度数．
【解答】解：∵AB∥CD，∠ACD＝80°，
∴∠BAC＝100°，
又∵AD平分∠BAC，
∴∠DAC＝ ∠BAC＝50°，
故答案为：50°．
本题主要考查了平行线的性质，以及角平分线的定义．解题时注意：两直线平行，同旁内角互补．
中考真题
谢谢
21世纪教育网（www.21cnjy.com) 中小学教育资源网站
有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php