1.3 证明（第1课时）同步课件

(共11张PPT)
1.3 证明

（第1课时）
浙教版 八年级上
新知导入



a
b














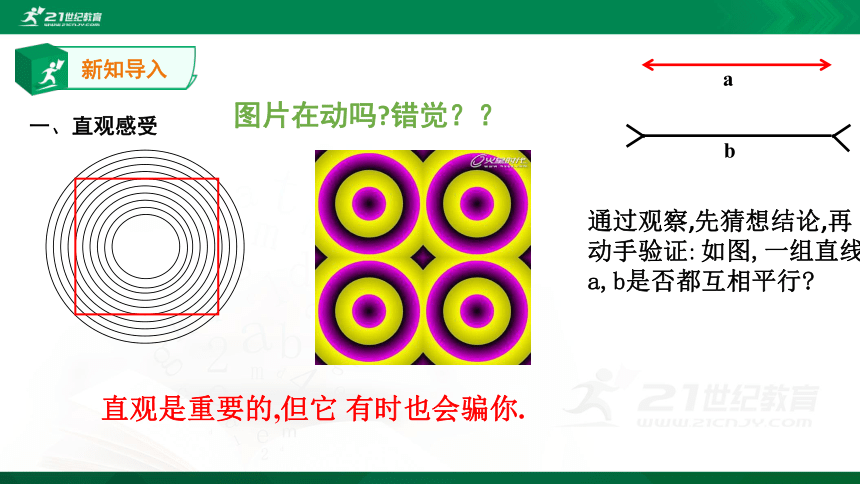
一、直观感受
图片在动吗?错觉？？
通过观察,先猜想结论,再动手验证: 如图,一组直线a,b是否都互相平行?
直观是重要的,但它 有时也会骗你.
新知导入
如何判断一个命题是真命题？
二、列举：例子太多无法写出存在的所有情况
一、目测（直观）:容易产生错觉
三、测量：选择工具不同，获得的结果也不尽相同
四、判定一个命题是真命题的方法:
通过推理的方式,即根据已知的事实来推断未知事实
新知导入
1.根据已知
2.依据已学
3.步步递推
4.证实判断
要判定一个命题是真命题，往往需要从命题的条件出发，根据已知的定义、基本事实、定理，一步一步推得结论成立，这样的推理过程叫做 证明 。
新知讲解
例1已知:如图1-12,DE∥BC,∠1=∠E求证:BE平分∠ABC
证明：
∵DE∥BC(已知)
∴∠2=∠E(两直线平行,内错角相等)
∵∠2=∠E(已知)
∴∠1=∠2
∴BE平分∠ABC(角平分线的定义)
新知讲解
证明几何命题的一般格式：
⑴按题意画出图形；
⑵分清命题的条件和结论，结合图形，在“已知”中写出条件，在“求证”中写出结论；
⑶在“证明”中写出推理过程。
新知讲解
解：
∵EF∥BC且∠AFE=64°
∴∠FCB=∠AFE=64°
∴∠EFC=180°-64°=116°
∵CE是△ABC的角平分线∴∠FCE=∠ECB=∠FCB=32°
∴∠FEC=180°-32°-116°32°
课堂练习
分析下列命题的条件和结论，画出图形，写出已知和求证
解析：
直角三角形斜边上的中线等于斜边的一半
已知：如图，△ＡＢＣ是直角三角形，且∠Ｃ＝９０°，

Ｄ是ＡＢ的中点

求证:ＣＤ＝　ＡＢ

Ｃ
Ａ
Ｂ
Ｄ

课堂总结
证明命题的一般步骤:
(1)理解题意:分清命题的条件(已知),结论(求证);
(2)根据题意,画出图形;
(3)结合图形,用符号语言写出“已知”和“求证”;
(4)分析题意,探索证明思路(由“因”导“果”,执“果”索“因”.);
(5)依据思路,运用数学符号和数学语言条理清晰地写出证明过程。
谢谢
21世纪教育网（www.21cnjy.com) 中小学教育资源网站
有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php