1.3 证明（第2课时）同步课件

(共16张PPT)
1.3 证明

（第2课时）
浙教版 八年级上
新知导入

A
B
C
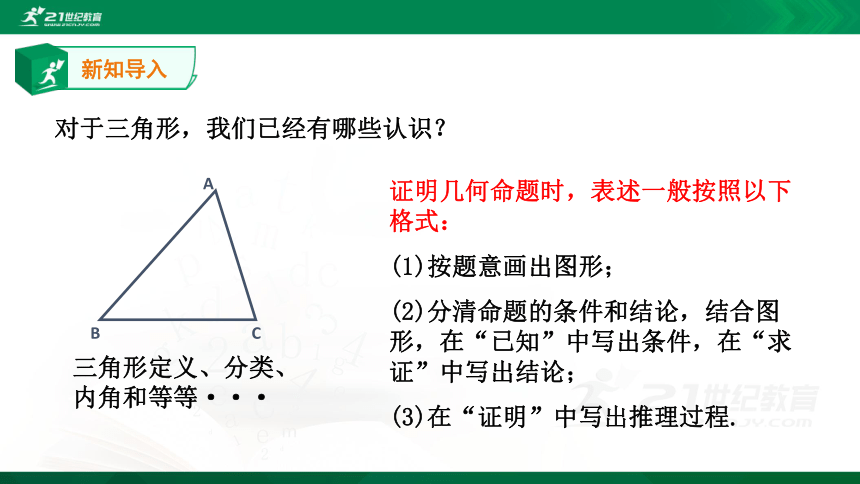
对于三角形，我们已经有哪些认识？
三角形定义、分类、内角和等等···

证明几何命题时，表述一般按照以下格式：
(1)按题意画出图形；
(2)分清命题的条件和结论，结合图形，在“已知”中写出条件，在“求证”中写出结论；
(3)在“证明”中写出推理过程.
新知导入
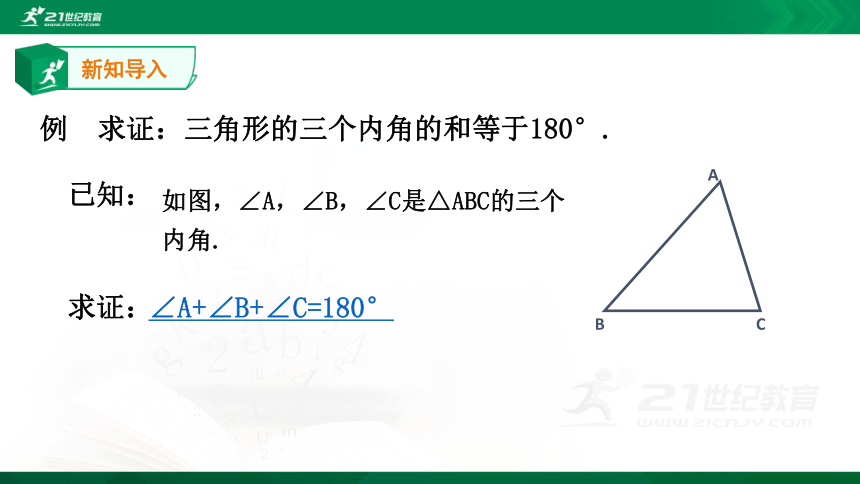
三角形的三个内角的和等于180°.
例 求证：

A
B
C
已知：
求证：
如图，∠A，∠B，∠C是△ABC的三个内角.
∠A+∠B+∠C=180°
已知:△ABC,如图：
求证:∠A+∠B+∠C=180°

证明:
过点A作直线 MN∥BC
∵MN∥BC
∴∠MAB=∠B,∠NAC=∠C(两直线平行,同位角相等),
∵∠MAB+∠BAC+∠NAC=180°(平角的定义）∴∠B+∠BAC+∠C=180°(等量代换),
即:三角形三个内角的和等于180°
新知导入



1
A
B
D




2
3
C




2
试一试：将纸片三角形顶角剪下，随意将它们拼凑在一起。








A
B
C
1
2
D
E

3



1


新知导入
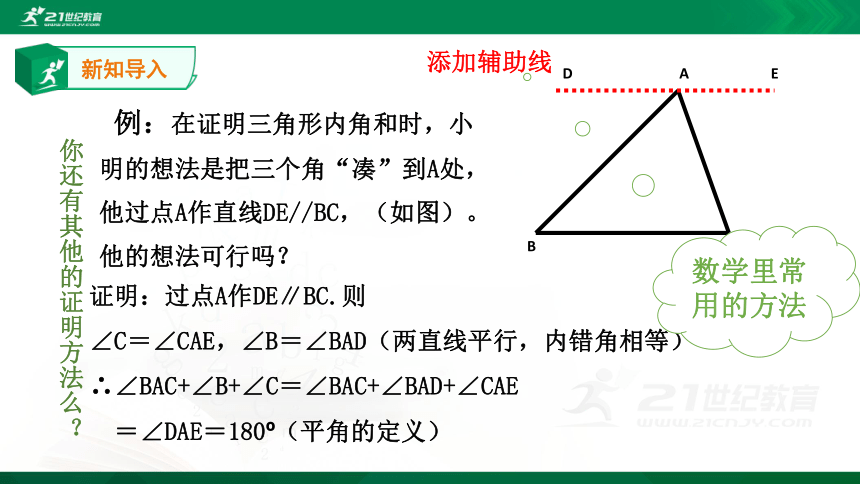
例：在证明三角形内角和时，小明的想法是把三个角“凑”到A处，他过点A作直线DE//BC，（如图）。他的想法可行吗？




A
B
C
E
D
证明：过点A作DE∥BC.则
∠C＝∠CAE，∠B＝∠BAD（两直线平行，内错角相等）
∴∠BAC+∠B+∠C＝∠BAC+∠BAD+∠CAE
　＝∠DAE＝180?（平角的定义）
添加辅助线
数学里常用的方法
你还有其他的证明方法么？
新知导入
已知：如图， △ABC.
求证：∠Ａ+∠Ｂ+∠Ｃ＝180°







A
B
C
1
2
D
E
∵ CE//AB
∴∠1＝∠Ａ（两直线平行，内错角相等）
∠2＝∠Ｂ（两直线平行，同位角相等）
∵ ∠1+∠2+∠ＡＣＢ＝180°
∴∠Ａ+∠Ｂ+∠ＡＣＢ＝180°
证明：延长BC到D，过点C作CE//AB
小结
辅助线：
3、添加辅助线，可构造新图形，形成新关系，找到联系已知与未知的桥梁，把问题转化，要根据需要而定,平时做题时要注意总结.
2、它的作用是把分散的条件集中，把隐含的条件显现出来，起到牵线搭桥的作用.
1、辅助线是为了证明需要在原图上添画的线.（辅助线通常画成虚线）
课堂总结
1.三角形内角和定理：三角形的三个内角的和等于180°.
2.三角形的一个外角等于和它不相邻的两个内角的和.
3.三角形的一个外角大于任何一个和它不相邻的内角.
课堂总结
1、三角形内角和定理:三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.

A
B
C


3、三角形的一个外角大于任何一个和它不相邻的内角
2、三角形的一个外角等于和它不相邻的两个内角的和







A
B
C
1
2
D
E
∵ ∠ACD 是△ABC的一个外角
∴∠ACD ＝ ∠Ａ+∠Ｂ
∵ ∠ACD 是△ABC的一个外角
∴ ∠ACD>∠A, ∠ACD>∠B
三角形内角和定理的几何表述：
证明的过程是用推理的方法证实证明题的过程,
因此每一步都要有依据,将思维过程较规范的表达出来需要注意的是在推理的过程中,
某一个推理既是前一个推理的“果”,
又作为后一个推理的“因”时,证明中这一步可以省略不写。
课堂总结
作业布置
练习1 在△ABC中，以A为顶点的一个外角为120°，∠B=50°，则∠C= °，请说明理由.



B
A
C
D
E



1
2
3



A
B
C
D
70°
练习2、如图，比较∠1 、∠2、∠3的大小，并证明你的判断.
作业布置
证明:
∵∠A=40°
∠BDC=75°(已知),
∠BDC=∠A+∠ABD(三角形的外角等于与它不相邻的两个内角的.）
∴∠ABD=75°-40°=35°
∵BD是∠ABC的平分线(已知)
∴∠DBC=∠ABD=35°(角平分线的定义)
∴∠ABC=70°
∴∠ACB=180°-70°-40°=70°(三角形三内角的和等于180°）
∴∠ABC=∠C
作业布置
解：
∵∠3=∠1+∠2(三角形的外角等于与它不相邻的两个内角的和),
∠1=∠2,∠3=100°(已知),
∴∠1=∠2=50°
此类题目考查了三角形外角的性质通过此题的证明过程,让同学们进一步理解三角形的外角等于与它不相邻的两个内角的和的知识
谢谢
21世纪教育网（www.21cnjy.com) 中小学教育资源网站
有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php