1.5 三角形全等的判定(第2课时)同步课件
文档属性
| 名称 | 1.5 三角形全等的判定(第2课时)同步课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-25 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
浙教版 八年级上
1.5 三角形全等的判定
(第2课时)
新知导入
1、全等三角形的性质:
2、全等三角形的判定:
全等三角形对应边相等,对应角相等。
三边对应相等的两个三角形全等
新知导入
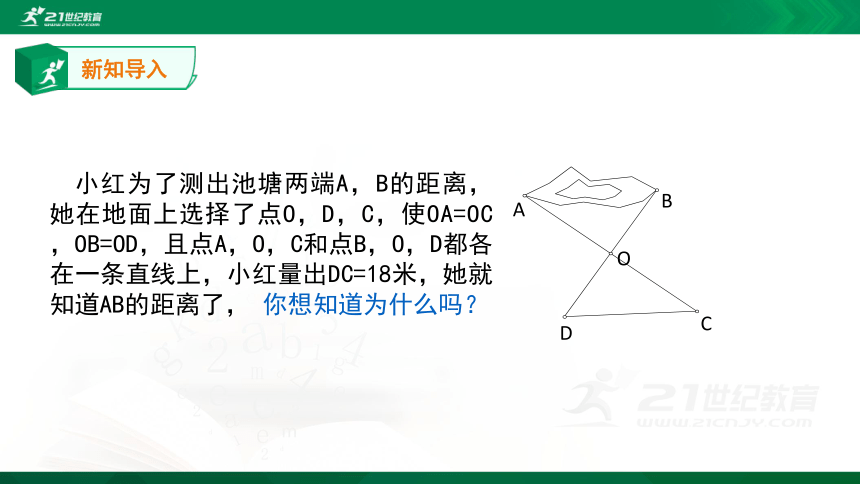
小红为了测出池塘两端A,B的距离,她在地面上选择了点O,D,C,使OA=OC,OB=OD,且点A,O,C和点B,O,D都各在一条直线上,小红量出DC=18米,她就知道AB的距离了, 你想知道为什么吗?
O
A
B
C
D
新知讲解
阅读课本第28至29页例3
1、我们有如下基本事实:两边及其夹角对应相等的两个三角形全等(简写成“边角边”或“SAS”定理)
2、在例3中要用边角边公理证明 △AOB≌△COD需要三个条件,这三个条件中,已具有两个条件,一是OA=OC(已知),二是___________;还需要一个条件_____________(这个条件可以证得吗?).
新课导入
画一画
用量角器和刻度尺画△ABC,使AB=4cm,BC=6cm, ∠ABC= 60°.
有一个角和夹这个角的两边对应相等的两个三角形全等(简写成“边角边”或“SAS”).
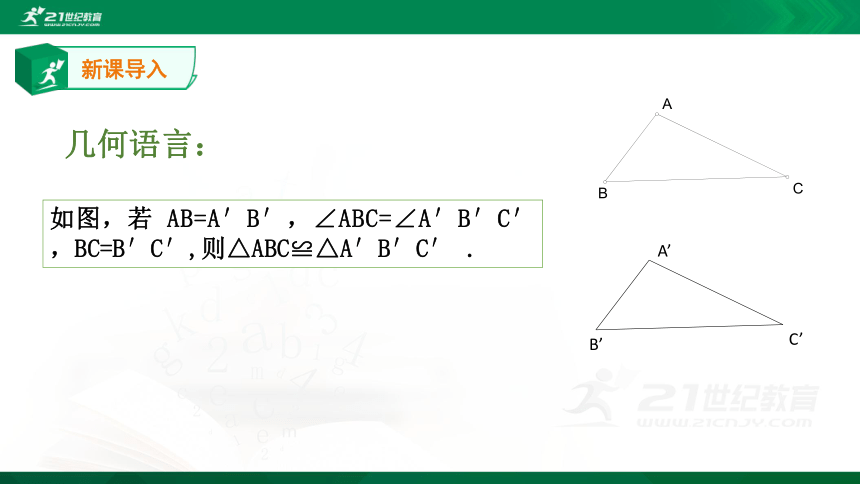
如图,若 AB=A′B′,∠ABC=∠A′B′C′,BC=B′C′,则△ABC≌△A′B′C′ .
A’
B’
C’
几何语言:
新课导入
拓展提高
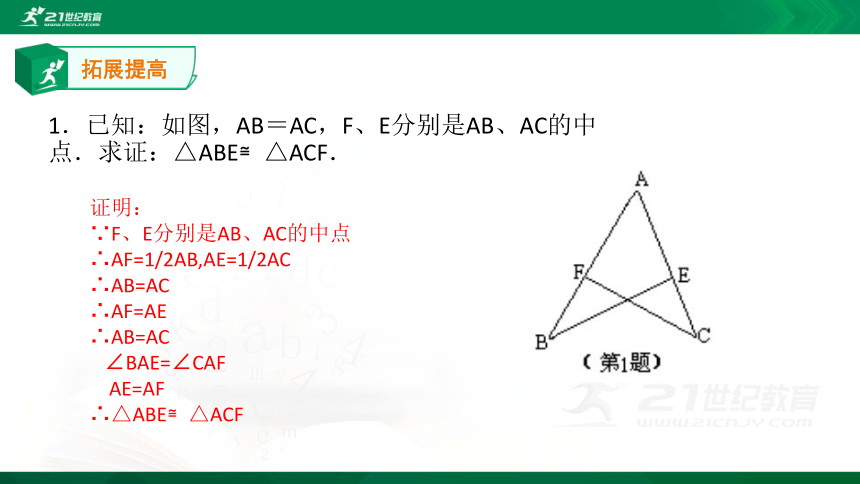
1.已知:如图,AB=AC,F、E分别是AB、AC的中点.求证:△ABE≌△ACF.
证明:
∵F、E分别是AB、AC的中点
∴AF=1/2AB,AE=1/2AC
∴AB=AC
∴AF=AE
∴AB=AC
∠BAE=∠CAF
AE=AF
∴△ABE≌△ACF
拓展提高
2.已知:点A、F、E、C在同一条直线上, AF=CE,BE∥DF,BE=DF.
求证:△ABE≌△CDF.
证明:
∵AF= CE.
∴AF+EF=CE+EF,即AE=CF
∵BE∥DF
∴∠DFE=∠FEB,
在△ABE与△CDF中
∴AE= CF
∠DFE=∠FEB
BE= DE
∴△ABE≌△CDF
拓展提高
线段垂直平分线的概念:
垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线.
线段垂直平分线的性质:
线段垂直平分线上的点到线段两端点的距离相等.
线段垂直平分线上的点到线段两端的距离相等吗?
B
O
C
l
A
拓展提高
如图,直线l⊥线段AB于点O,且OA=OB,点C是直线l上任意一点,说明CA=CB的理由.
总结:①分析题意时,应注意由条件所可能产生的结论,如:已知垂直,可得90°的角.
②结合图形,善于找出图中“天然”的条件,如:对顶角、公共边等.
B
O
C
l
A
课堂练习
1.如图,AB,CD相交于点O,OA=OB,OC=OD,请问∠ A和∠B相等吗?AC与BD相等吗?为什么?
相等
理由:
在△AOC与△BOD中,
∵OA=OB
∠AOC=∠BOD
OC=OD
∴△AOC△BOD
∴AC= BD
课堂练习
2、四边形ABCD中AB=DC,AD=BC,E、F在直线BD上,且BE=DF。如图在ABCD中,点E、F在对角线BD上且△ABD≌△CDB,说明∠E=∠F
证明:
∵△ABD≌△CDB
∴∠ABD=∠CDB
∠ABE=∠CDF
又∵AB=CD
BE=DF
∴由SAS,得△ABE≌△CDF
∴∠E=∠F
3.如图,已知AB⊥BD,ED⊥CD,且AB=CD,BC=DE,请问△ABC是否全等于△CDE?AC是否垂直于CE?为什么?
课堂练习
△ABC≌△CDE,AC⊥CE
理由:
∵AB⊥BD,ED⊥CD,
∴∠B=∠D=90°
∵AB=CD,BC=DE,
∴△ABC△CDB(SAS)
∴∠DCE=∠A
∴∠A+∠ACB=90°,
∴∠DCE+∠ACB=90°
∵∠DCE+∠ACB+∠ACE=180°
∵.∠ACE=90° ∴AC⊥CE.
∵ 点C在线段AB的垂直平分线上 ,
∴ CA=CB.
说明两线段相等的一种重要方法.
几何语言:
课堂总结
(2019浙江嘉兴中考)如图,在矩形ABCD中,点E,F在对角线BD.请添加一个条件,使得结论“AE=CF”成立,并加以证明.
中考真题
【分析】根据SAS即可证明△ABE≌△CDF可得AE=CF.
【解答】解:添加的条件是BE=DF(答案不唯一).
证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
∴∠ABD=∠BDC,
又∵BE=DF(添加),
∴△ABE≌△CDF(SAS),
∴AE=CF.
【点评】本题考查矩形的性质、全等三角形的判定和性质等知识,解题的关键是熟练掌握全等三角形的判定方法,属于中考常考题型.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
浙教版 八年级上
1.5 三角形全等的判定
(第2课时)
新知导入
1、全等三角形的性质:
2、全等三角形的判定:
全等三角形对应边相等,对应角相等。
三边对应相等的两个三角形全等
新知导入
小红为了测出池塘两端A,B的距离,她在地面上选择了点O,D,C,使OA=OC,OB=OD,且点A,O,C和点B,O,D都各在一条直线上,小红量出DC=18米,她就知道AB的距离了, 你想知道为什么吗?
O
A
B
C
D
新知讲解
阅读课本第28至29页例3
1、我们有如下基本事实:两边及其夹角对应相等的两个三角形全等(简写成“边角边”或“SAS”定理)
2、在例3中要用边角边公理证明 △AOB≌△COD需要三个条件,这三个条件中,已具有两个条件,一是OA=OC(已知),二是___________;还需要一个条件_____________(这个条件可以证得吗?).
新课导入
画一画
用量角器和刻度尺画△ABC,使AB=4cm,BC=6cm, ∠ABC= 60°.
有一个角和夹这个角的两边对应相等的两个三角形全等(简写成“边角边”或“SAS”).
如图,若 AB=A′B′,∠ABC=∠A′B′C′,BC=B′C′,则△ABC≌△A′B′C′ .
A’
B’
C’
几何语言:
新课导入
拓展提高
1.已知:如图,AB=AC,F、E分别是AB、AC的中点.求证:△ABE≌△ACF.
证明:
∵F、E分别是AB、AC的中点
∴AF=1/2AB,AE=1/2AC
∴AB=AC
∴AF=AE
∴AB=AC
∠BAE=∠CAF
AE=AF
∴△ABE≌△ACF
拓展提高
2.已知:点A、F、E、C在同一条直线上, AF=CE,BE∥DF,BE=DF.
求证:△ABE≌△CDF.
证明:
∵AF= CE.
∴AF+EF=CE+EF,即AE=CF
∵BE∥DF
∴∠DFE=∠FEB,
在△ABE与△CDF中
∴AE= CF
∠DFE=∠FEB
BE= DE
∴△ABE≌△CDF
拓展提高
线段垂直平分线的概念:
垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线.
线段垂直平分线的性质:
线段垂直平分线上的点到线段两端点的距离相等.
线段垂直平分线上的点到线段两端的距离相等吗?
B
O
C
l
A
拓展提高
如图,直线l⊥线段AB于点O,且OA=OB,点C是直线l上任意一点,说明CA=CB的理由.
总结:①分析题意时,应注意由条件所可能产生的结论,如:已知垂直,可得90°的角.
②结合图形,善于找出图中“天然”的条件,如:对顶角、公共边等.
B
O
C
l
A
课堂练习
1.如图,AB,CD相交于点O,OA=OB,OC=OD,请问∠ A和∠B相等吗?AC与BD相等吗?为什么?
相等
理由:
在△AOC与△BOD中,
∵OA=OB
∠AOC=∠BOD
OC=OD
∴△AOC△BOD
∴AC= BD
课堂练习
2、四边形ABCD中AB=DC,AD=BC,E、F在直线BD上,且BE=DF。如图在ABCD中,点E、F在对角线BD上且△ABD≌△CDB,说明∠E=∠F
证明:
∵△ABD≌△CDB
∴∠ABD=∠CDB
∠ABE=∠CDF
又∵AB=CD
BE=DF
∴由SAS,得△ABE≌△CDF
∴∠E=∠F
3.如图,已知AB⊥BD,ED⊥CD,且AB=CD,BC=DE,请问△ABC是否全等于△CDE?AC是否垂直于CE?为什么?
课堂练习
△ABC≌△CDE,AC⊥CE
理由:
∵AB⊥BD,ED⊥CD,
∴∠B=∠D=90°
∵AB=CD,BC=DE,
∴△ABC△CDB(SAS)
∴∠DCE=∠A
∴∠A+∠ACB=90°,
∴∠DCE+∠ACB=90°
∵∠DCE+∠ACB+∠ACE=180°
∵.∠ACE=90° ∴AC⊥CE.
∵ 点C在线段AB的垂直平分线上 ,
∴ CA=CB.
说明两线段相等的一种重要方法.
几何语言:
课堂总结
(2019浙江嘉兴中考)如图,在矩形ABCD中,点E,F在对角线BD.请添加一个条件,使得结论“AE=CF”成立,并加以证明.
中考真题
【分析】根据SAS即可证明△ABE≌△CDF可得AE=CF.
【解答】解:添加的条件是BE=DF(答案不唯一).
证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
∴∠ABD=∠BDC,
又∵BE=DF(添加),
∴△ABE≌△CDF(SAS),
∴AE=CF.
【点评】本题考查矩形的性质、全等三角形的判定和性质等知识,解题的关键是熟练掌握全等三角形的判定方法,属于中考常考题型.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
