1.5 三角形全等的判定(第3课时)同步课件
文档属性
| 名称 | 1.5 三角形全等的判定(第3课时)同步课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-25 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
浙教版 八年级上
1.5 三角形全等的判定
(第3课时)
新知导入
1.判断三角形全等至少要有几个条件?
至少要有三个条件.
2.全等三角形的性质:
3.三角形全等的判定方法有哪些?
全等三角形对应边相等,对应角相等。
判定1、三边对应相等的两个三角形全等(SSS)
判定2、两边及其夹角相等的两个三角形全等(SAS)
新知导入
如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适?你能说明其中理由吗?
右边那块,也就是有两个角的那块
新知导入
如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
①角边角
②角角边
新知讲解
E
G
F
600
450
3cm
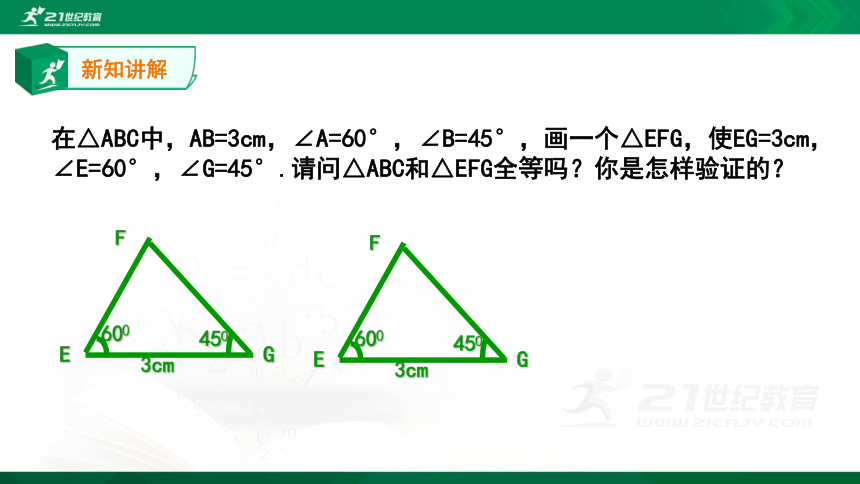
在△ABC中,AB=3cm,∠A=60°,∠B=45°,画一个△EFG,使EG=3cm,∠E=60°,∠G=45°.请问△ABC和△EFG全等吗?你是怎样验证的?
E
G
F
600
450
3cm
新知讲解
判定3:有两个角和这两个角的夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”).
课堂练习
已知:如图,点B,C,F,E在同一直线上,
AC〃DF,且AC=DF, ∠A=∠D,求证:AB=DE
证明:
∵AC∥DF
∴∠ACB=∠DF
在△ABC和△DEF中,
∵∠A=∠D
AC=DF
∠ACB=∠DEF
∴△ABC≌△DEF(ASA)
∴AB=DE
课堂练习
已知:如图,∠1=∠2, ∠C=∠E, AC=AE,
求证:△ABC≌△ADE
证明:
∵∠1=∠2
∴∠1+∠EAC=∠2+∠EAC
∵∠BAC=∠DAE
∵AC=AE,∠C=∠E
∴△ABC≌△ADE
拓展练习
例5 已知:如图,点B,F,E,C在同一条直线,AB∥CD,且AB=CD,∠A=∠D. 求证:AE=DF.
(2019江苏南京中考)如图,D是△ABC的边AB的中点,DE∥BC,CE∥AB,AC与DE相交于点F.求证:△ADF≌△CEF.
中考真题
【分析】依据四边形DBCE是平行四边形,即可得出BD=CE,依据CE∥AD,即可得出∠A=∠ECF,∠ADF=∠E,即可判定△ADF≌△CEF.
证明:∵DE∥BC,CE∥AB,
∴四边形DBCE是平行四边形,
∴BD=CE,
∵D是AB的中点,
∴AD=BD,
∴AD=EC,
∵CE∥AD,
∴∠A=∠ECF,∠ADF=∠E, ∴△ADF≌△CEF(ASA).
中考真题
(2019四川成都)如图,在△ABC中,AB=AC,点D,E都在边BC上,∠BAD=∠CAE,若BD=9,则CE的长为______.
解:∵AB=AC,
∴∠B=∠C,
在△BAD和△CAE中,
∴△BAD≌△CAE,
∴BD=CE=9,
故答案为:9.
利用等腰三角形的性质和题目的已知条件证得△BAD≌△CAE后即可求得CE的长.
本题考查了等腰三角形的性质,解题的关键是利用已知和隐含条件证得三角形全等.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
浙教版 八年级上
1.5 三角形全等的判定
(第3课时)
新知导入
1.判断三角形全等至少要有几个条件?
至少要有三个条件.
2.全等三角形的性质:
3.三角形全等的判定方法有哪些?
全等三角形对应边相等,对应角相等。
判定1、三边对应相等的两个三角形全等(SSS)
判定2、两边及其夹角相等的两个三角形全等(SAS)
新知导入
如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适?你能说明其中理由吗?
右边那块,也就是有两个角的那块
新知导入
如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
①角边角
②角角边
新知讲解
E
G
F
600
450
3cm
在△ABC中,AB=3cm,∠A=60°,∠B=45°,画一个△EFG,使EG=3cm,∠E=60°,∠G=45°.请问△ABC和△EFG全等吗?你是怎样验证的?
E
G
F
600
450
3cm
新知讲解
判定3:有两个角和这两个角的夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”).
课堂练习
已知:如图,点B,C,F,E在同一直线上,
AC〃DF,且AC=DF, ∠A=∠D,求证:AB=DE
证明:
∵AC∥DF
∴∠ACB=∠DF
在△ABC和△DEF中,
∵∠A=∠D
AC=DF
∠ACB=∠DEF
∴△ABC≌△DEF(ASA)
∴AB=DE
课堂练习
已知:如图,∠1=∠2, ∠C=∠E, AC=AE,
求证:△ABC≌△ADE
证明:
∵∠1=∠2
∴∠1+∠EAC=∠2+∠EAC
∵∠BAC=∠DAE
∵AC=AE,∠C=∠E
∴△ABC≌△ADE
拓展练习
例5 已知:如图,点B,F,E,C在同一条直线,AB∥CD,且AB=CD,∠A=∠D. 求证:AE=DF.
(2019江苏南京中考)如图,D是△ABC的边AB的中点,DE∥BC,CE∥AB,AC与DE相交于点F.求证:△ADF≌△CEF.
中考真题
【分析】依据四边形DBCE是平行四边形,即可得出BD=CE,依据CE∥AD,即可得出∠A=∠ECF,∠ADF=∠E,即可判定△ADF≌△CEF.
证明:∵DE∥BC,CE∥AB,
∴四边形DBCE是平行四边形,
∴BD=CE,
∵D是AB的中点,
∴AD=BD,
∴AD=EC,
∵CE∥AD,
∴∠A=∠ECF,∠ADF=∠E, ∴△ADF≌△CEF(ASA).
中考真题
(2019四川成都)如图,在△ABC中,AB=AC,点D,E都在边BC上,∠BAD=∠CAE,若BD=9,则CE的长为______.
解:∵AB=AC,
∴∠B=∠C,
在△BAD和△CAE中,
∴△BAD≌△CAE,
∴BD=CE=9,
故答案为:9.
利用等腰三角形的性质和题目的已知条件证得△BAD≌△CAE后即可求得CE的长.
本题考查了等腰三角形的性质,解题的关键是利用已知和隐含条件证得三角形全等.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
