1.5 三角形全等的判定(第4课时)同步课件
文档属性
| 名称 | 1.5 三角形全等的判定(第4课时)同步课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-25 17:51:03 | ||
图片预览





文档简介
(共14张PPT)
浙教版 八年级上
1.5 三角形全等的判定
(第4课时)
新知导入
1、全等三角形的性质: 。
2、三角形全等的判定方法有哪些?
全等三角形对应边相等,对应角相等。
判定1、三边对应相等的两个三角形全等(SSS)
判定2、两边及其夹角相等的两个三角形全等(SAS)
判定3、两角及其夹边相等的两个三角形全等(ASA)
用来判定两个三角形全等还有其它判定吗?
新知讲解
在ΔABC和Δ DEF中,
∠A= ∠D,
AC=DF,
∠C=∠F,
解 ∵ ∠A+∠B+∠C=180°,
∠D+∠E+∠F=180°,
(三角形的内角和等于180°)
A
B
C
D
E
F
在ΔABC和ΔDEF中,∠B=∠E,∠C=∠F,AC=DF,请说明ΔABC≌ΔDEF.
∴ ∠A=180°-∠B-∠C,
∠D=180°-∠E-∠F.
∵ ∠B=∠E ,∠C=∠F,
∴ ∠A= ∠D.
∴ΔABC≌ΔDEF(ASA).
阅读课本第34页
1、我们有如下推论:
两角及其中一个角的对边对应相等的两个三角形全等(简写成“角角边”或“AAS”定理)
你能通过基本事实“ASA”判定定理推出 “AAS”定理吗?
2、在例6中要证明PB=PC只需证明 ?需要三个条件,这三个条件中,已具有一个条件,这是___________;还需要两个条件 ____________
(这两个条件可以证得吗?).
△ABP≌△ACP
公共边AP=AP
∠APB=∠ACP=90度, ∠PAC=∠PAB
新知讲解
判定4:有两个角和其中一个角的对边对应相等的两个三角形全等(简写成“角角边”或“AAS”).
课堂练习
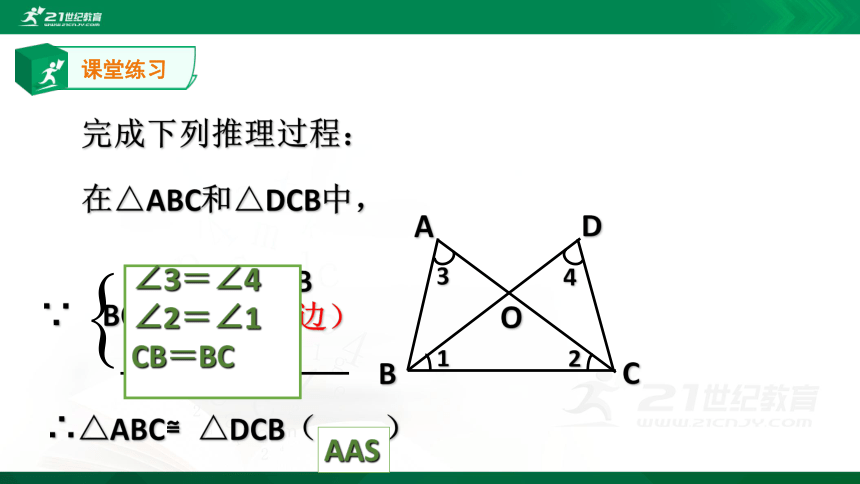
完成下列推理过程:
在△ABC和△DCB中,
∠ABC=∠DCB
∵ BC=CB
∴△ABC≌△DCB( )
A
B
C
D
O
1
2
3
4
AAS
(公共边)
∠2=∠1
∠3=∠4
∠2=∠1
CB=BC
拓展提高
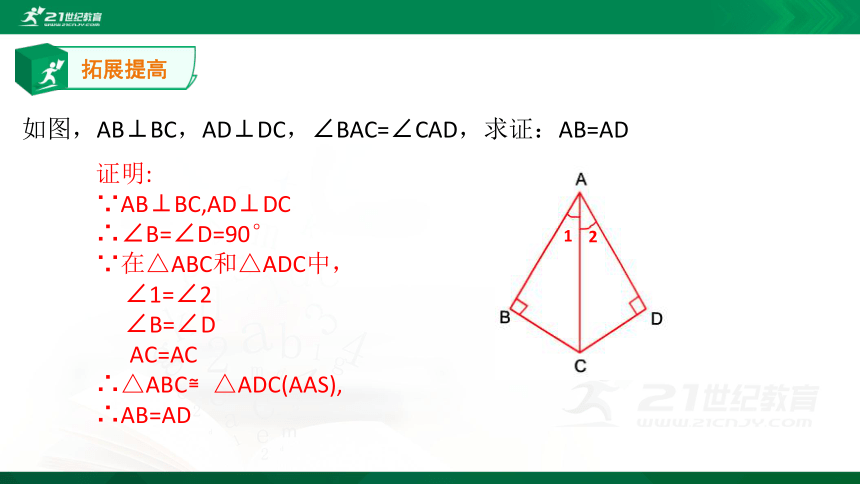
如图,AB⊥BC,AD⊥DC,∠BAC=∠CAD,求证:AB=AD
1
2
证明:
∵AB⊥BC,AD⊥DC
∴∠B=∠D=90°
∵在△ABC和△ADC中,
∠1=∠2
∠B=∠D
AC=AC
∴△ABC≌△ADC(AAS),
∴AB=AD
如图,点P是∠BAC的平分线上的一点,PB⊥AB,PC⊥AC.说明PB=PC的理由.
解 ∵ PB⊥AB,PC⊥AC,
∴ ∠ABP=∠ACP(垂线的意义),
在ΔABP和ΔACP中,
∠PAB=∠PAC (角平分线的意义),
∠ABP=∠ACP,
AP=AP(公共边),
∴ ΔABP≌ΔACP(AAS).
∴ PB=PC(全等三角形的对应边相等).
拓展提高
课堂总结
角平分线上的点到角两边的距离相等.
应 用
∵P 是∠BAC的平分线上的点,
PB⊥AB,PC⊥AC,∴PB=PC(角平分线上的点到角
两边的距离相等).
课堂总结
(1) 两角和它们的夹边对应相等的两个三角形全等.
简写成“角边角”或“ASA”.
(2) 两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
(3)探索三角形全等是证明线段相等(对应边相等),
角相等(对应角相等)等问题的基本途径.
拓展提高
如图,AB∥CD,PB和PC分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.求证:PA=PD
证明:
过点P作PB⊥BC于E
∵AB∥CD,PA⊥AB
∴PD⊥CDPB和PC分别平分∠ABC和∠DCB
∴PA=PE
PD=PE
∴PA-=PD
中考真题
(2019重庆中考)如图,在平行四边形ABCD中,点E在边BC上,连结AE,EM⊥AE,垂足为E,交CD于点M,AF⊥BC,垂足为F,BH⊥AE,垂足为H,交AF于点N,点P是AD上一点,连接CP.证明△NBF≌△EAF
证明:连接NE,
∵AH⊥AE,AF⊥BC,AE⊥EM,
∴∠AEB+∠NBF=∠AEB+∠EAF=∠AEB+∠MEC=90°,
∴∠NBF=∠EAF=∠MEC,
在△NBF和△EAF中,
∴△NBF≌△EAF(AAS)
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
浙教版 八年级上
1.5 三角形全等的判定
(第4课时)
新知导入
1、全等三角形的性质: 。
2、三角形全等的判定方法有哪些?
全等三角形对应边相等,对应角相等。
判定1、三边对应相等的两个三角形全等(SSS)
判定2、两边及其夹角相等的两个三角形全等(SAS)
判定3、两角及其夹边相等的两个三角形全等(ASA)
用来判定两个三角形全等还有其它判定吗?
新知讲解
在ΔABC和Δ DEF中,
∠A= ∠D,
AC=DF,
∠C=∠F,
解 ∵ ∠A+∠B+∠C=180°,
∠D+∠E+∠F=180°,
(三角形的内角和等于180°)
A
B
C
D
E
F
在ΔABC和ΔDEF中,∠B=∠E,∠C=∠F,AC=DF,请说明ΔABC≌ΔDEF.
∴ ∠A=180°-∠B-∠C,
∠D=180°-∠E-∠F.
∵ ∠B=∠E ,∠C=∠F,
∴ ∠A= ∠D.
∴ΔABC≌ΔDEF(ASA).
阅读课本第34页
1、我们有如下推论:
两角及其中一个角的对边对应相等的两个三角形全等(简写成“角角边”或“AAS”定理)
你能通过基本事实“ASA”判定定理推出 “AAS”定理吗?
2、在例6中要证明PB=PC只需证明 ?需要三个条件,这三个条件中,已具有一个条件,这是___________;还需要两个条件 ____________
(这两个条件可以证得吗?).
△ABP≌△ACP
公共边AP=AP
∠APB=∠ACP=90度, ∠PAC=∠PAB
新知讲解
判定4:有两个角和其中一个角的对边对应相等的两个三角形全等(简写成“角角边”或“AAS”).
课堂练习
完成下列推理过程:
在△ABC和△DCB中,
∠ABC=∠DCB
∵ BC=CB
∴△ABC≌△DCB( )
A
B
C
D
O
1
2
3
4
AAS
(公共边)
∠2=∠1
∠3=∠4
∠2=∠1
CB=BC
拓展提高
如图,AB⊥BC,AD⊥DC,∠BAC=∠CAD,求证:AB=AD
1
2
证明:
∵AB⊥BC,AD⊥DC
∴∠B=∠D=90°
∵在△ABC和△ADC中,
∠1=∠2
∠B=∠D
AC=AC
∴△ABC≌△ADC(AAS),
∴AB=AD
如图,点P是∠BAC的平分线上的一点,PB⊥AB,PC⊥AC.说明PB=PC的理由.
解 ∵ PB⊥AB,PC⊥AC,
∴ ∠ABP=∠ACP(垂线的意义),
在ΔABP和ΔACP中,
∠PAB=∠PAC (角平分线的意义),
∠ABP=∠ACP,
AP=AP(公共边),
∴ ΔABP≌ΔACP(AAS).
∴ PB=PC(全等三角形的对应边相等).
拓展提高
课堂总结
角平分线上的点到角两边的距离相等.
应 用
∵P 是∠BAC的平分线上的点,
PB⊥AB,PC⊥AC,∴PB=PC(角平分线上的点到角
两边的距离相等).
课堂总结
(1) 两角和它们的夹边对应相等的两个三角形全等.
简写成“角边角”或“ASA”.
(2) 两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
(3)探索三角形全等是证明线段相等(对应边相等),
角相等(对应角相等)等问题的基本途径.
拓展提高
如图,AB∥CD,PB和PC分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.求证:PA=PD
证明:
过点P作PB⊥BC于E
∵AB∥CD,PA⊥AB
∴PD⊥CDPB和PC分别平分∠ABC和∠DCB
∴PA=PE
PD=PE
∴PA-=PD
中考真题
(2019重庆中考)如图,在平行四边形ABCD中,点E在边BC上,连结AE,EM⊥AE,垂足为E,交CD于点M,AF⊥BC,垂足为F,BH⊥AE,垂足为H,交AF于点N,点P是AD上一点,连接CP.证明△NBF≌△EAF
证明:连接NE,
∵AH⊥AE,AF⊥BC,AE⊥EM,
∴∠AEB+∠NBF=∠AEB+∠EAF=∠AEB+∠MEC=90°,
∴∠NBF=∠EAF=∠MEC,
在△NBF和△EAF中,
∴△NBF≌△EAF(AAS)
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
