2.8 直角三角形的全等判定 同步课件

课件15张PPT。浙教版 八年级上 2.8 直角三角形的全等判定
新知导入1、三边对应对应相等 SSS
2、两角及其夹边对应相等 ASA
3、两角及其中一角的对边对应相等 AAS
4、两边及其夹角对应相等 SAS
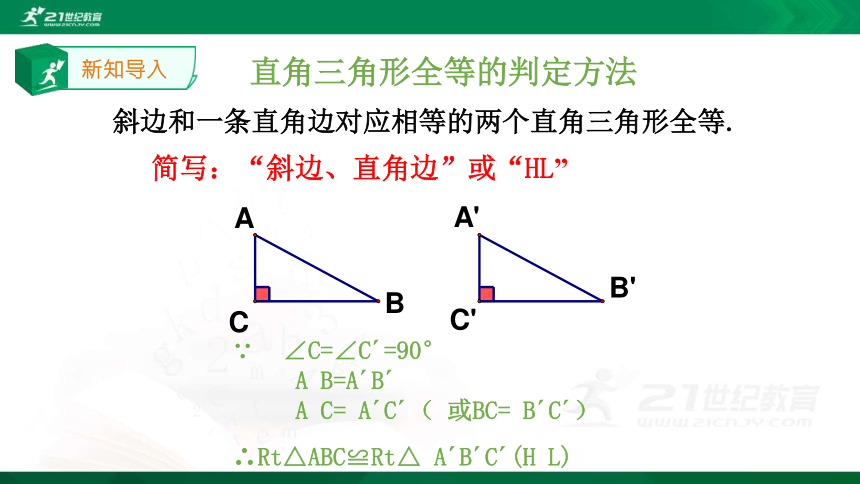
我们之前学的三角形全等的判定定理有哪些? 看下图，具有下列条件的Rt△ABC和Rt△A’B’C’是否全等？ 有两条边对应相等的两个三角形全等吗? 新知导入新知导入斜边和一条直角边对应相等的两个直角三角形全等.简写：“斜边、直角边”或“HL”∠C=∠C′=90°
A B=A′B′
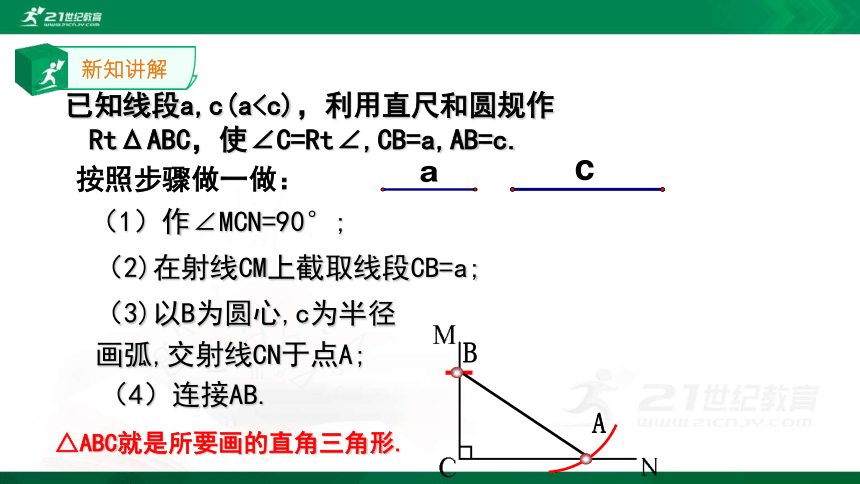
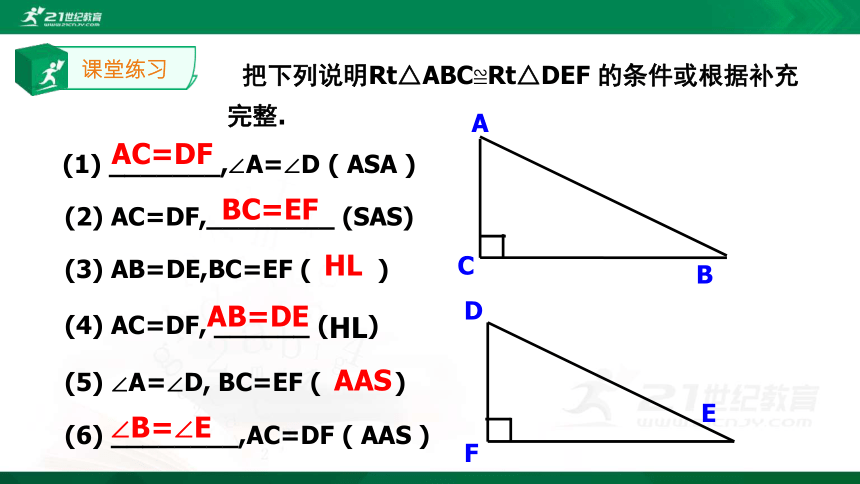
A C= A′C′（ 或BC= B′C′）∴Rt△ABC≌Rt△ A′B′C′(H L)直角三角形全等的判定方法∵新知讲解已知线段a,c(a画弧,交射线CN于点A; （4）连接AB.△ABC就是所要画的直角三角形.课堂练习 (1) _______,∠A=∠D ( ASA )
(2) AC=DF,________ (SAS)
(3) AB=DE,BC=EF ( )
(4) AC=DF, ______ (HL)
(5) ∠A=∠D, BC=EF ( )
(6) ________,AC=DF ( AAS ) 把下列说明Rt△ABC≌Rt△DEF 的条件或根据补充完整. AC=DF BC=EF HL AB=DE AAS ∠B=∠E拓展提高 在使用“HL”时,同学们应注意什么?
“HL”是仅适用于直角三角形的特殊方法.
注意对应相等.
因为”HL”仅适用直角三角形,
书写格式应为:
∵在Rt△ABC与Rt△DEF中
AB =DE
AC=DF
∴Rt△ABC≌Rt△DEF (HL)拓展提高 角的内部，到角两边距离相等的点，在这个角的平分线上。角平分线性质定理：∴PD=PE（角平分线性质）∵OP平分∠AOB拓展提高如图，AB⊥BD于点B，CD⊥BD于点D，P是BD上一点，且AP=PC，AP⊥PC，则△ABP≌△PDC，请说明理由。思路：
①∠ABP=∠CDP=90°
② AP=PC课后作业2、再过点M作OA的垂线,1、如图:在已知∠AOB的两边OA,OB上
分别取点M,N,使OM=ON;3、过点N作OB的垂线,两垂线交于点P,4、那么射线OP就是∠AOB的平分线.P●用一个三角板作任意角的角平分线：角平分线性质：角的内部，到角两边距离相等的点，在这个角的平分线上。中考真题（2019甘肃中考）如图，在正方形ABCD中，点E是BC的中点，连接DE，过点A作AG⊥ED交DE于点F，交CD于点G．
（1）证明：△ADG≌△DCE；解析：
本题主要考查了正方形的性质以及全等三角形的判定与性质，在应用全等三角形的判定时，要注意三角形间的公共边和公共角中考真题解：（1）∵四边形ABCD是正方形，
∴∠ADG＝∠C＝90°，AD＝DC，
又∵AG⊥DE，
∴∠DAG+∠ADF＝90°＝∠CDE+∠ADF，
∴∠DAG＝∠CDE，
∴△ADG≌△DCE（ASA）（2019黑龙江龙东中考）一张直角三角形纸片ABC，∠ACB＝90°，AB＝10，AC＝6，点D为BC边上的任一点，沿过点D的直线折叠，使直角顶点C落在斜边AB上的点E处，当△BDE是直角三角形时，则CD的长为　 　．中考真题解：
若∠DEB＝90°，则∠AED＝90°＝∠C，CD＝ED，
连接AD，则Rt△ACD≌Rt△AED（HL），
∴AE＝AC＝6，BE＝10﹣6＝4，
设CD＝DE＝x，则BD＝8﹣x，
∵Rt△BDE中，DE2+BE2＝BD2，
∴x2+42＝（8﹣x）2，
解得x＝3，
∴CD＝3；
两个考点：全等+勾股定理谢谢21世纪教育网（www.21cnjy.com) 中小学教育资源网站 有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php