浙教版八年级数学上册第二章特殊三角形 2.3等腰三角形的性质定理课件共18张
文档属性
| 名称 | 浙教版八年级数学上册第二章特殊三角形 2.3等腰三角形的性质定理课件共18张 |

|
|
| 格式 | zip | ||
| 文件大小 | 174.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-03 00:00:00 | ||
图片预览

文档简介
课件18张PPT。2.3等腰三角形的
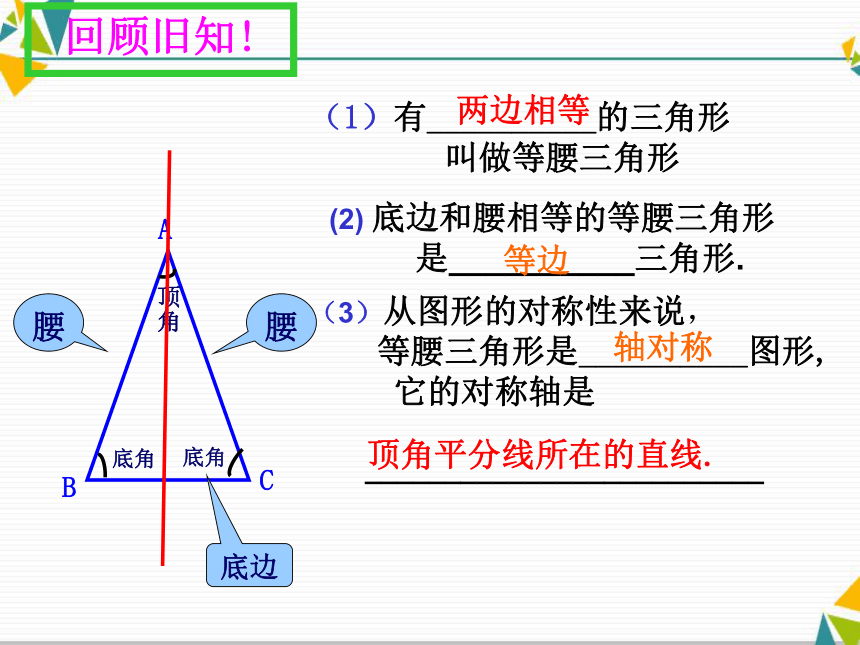
性质定理(1)有__________的三角形
叫做等腰三角形底边
(3)从图形的对称性来说,
等腰三角形是__________图形,
它的对称轴是
_________________________
顶角平分线所在的直线.
(2) 底边和腰相等的等腰三角形
是__________三角形.等边两边相等轴对称回顾旧知! 已知:在△ABC中,AB=AC
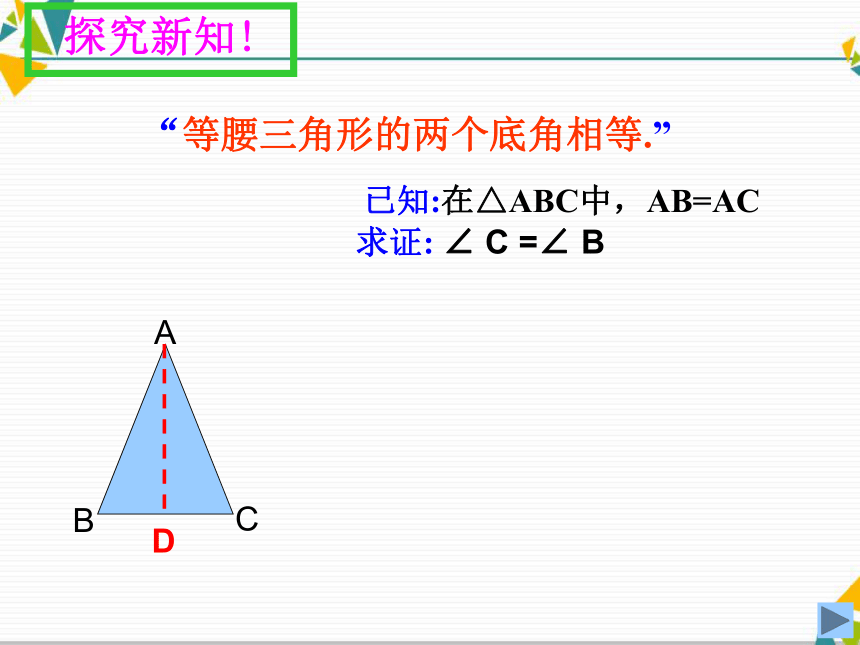
求证: ∠ C =∠ BD“等腰三角形的两个底角相等.” 探究新知! 已知:如图,?ABC中, AB=AC
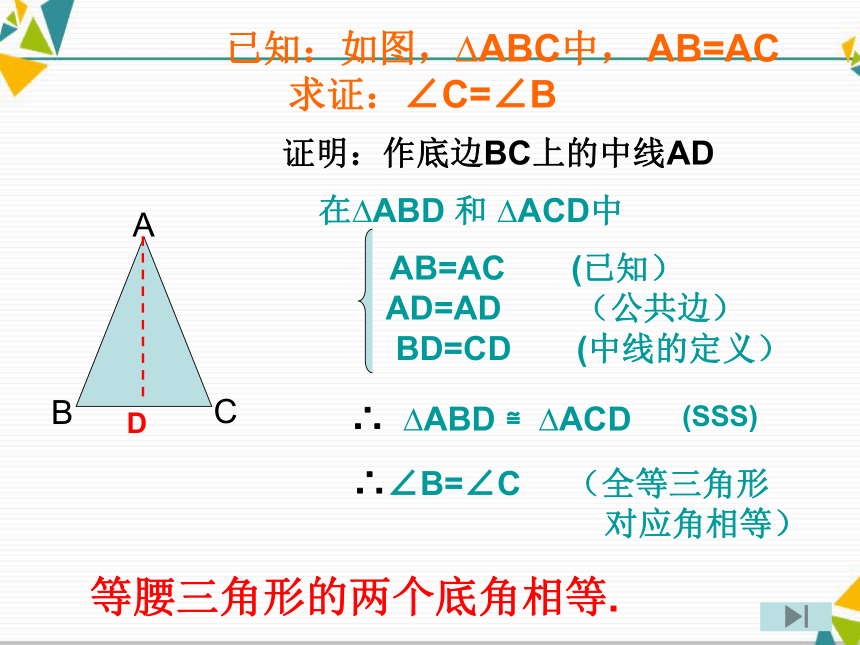
求证:∠C=∠BD证明:作底边BC上的中线AD AB=AC (已知)
AD=AD (公共边)
BD=CD (中线的定义)∴ ?ABD ≌?ACD ∴∠B=∠C (全等三角形
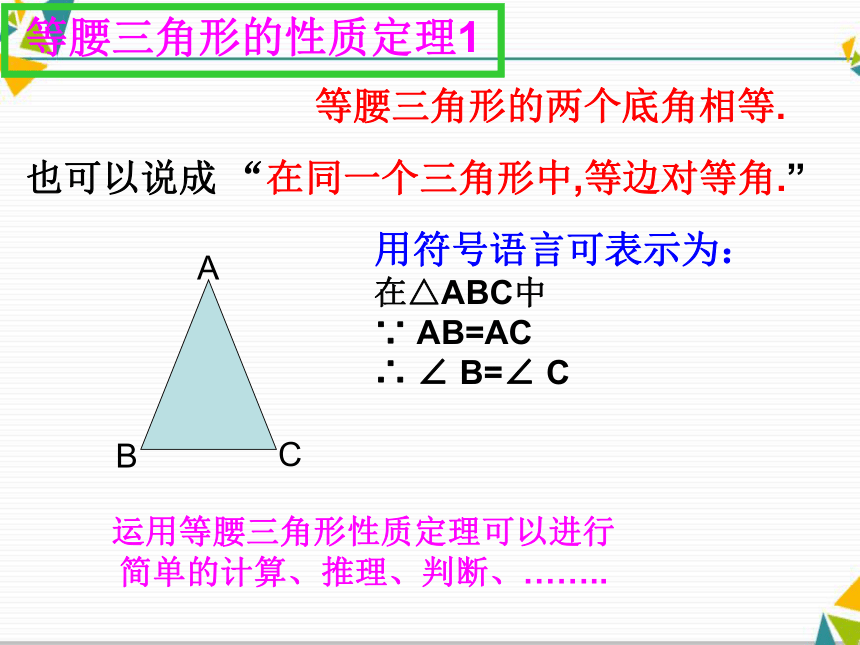
对应角相等)(SSS)在?ABD 和 ?ACD中等腰三角形的两个底角相等.等腰三角形的性质定理1 等腰三角形的两个底角相等.也可以说成 “在同一个三角形中,等边对等角.”
用符号语言可表示为:
在△ABC中
∵ AB=AC
∴ ∠ B=∠ C
运用等腰三角形性质定理可以进行
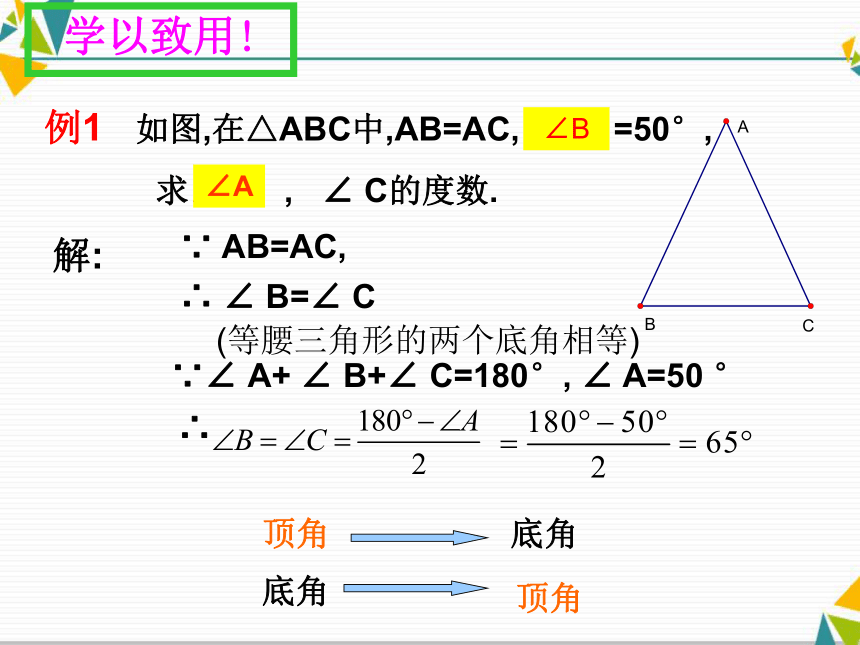
简单的计算、推理、判断、……..例1 如图,在△ABC中,AB=AC, ∠A =50°,
求∠ B , ∠ C的度数. 解:∵ AB=AC,∴ ∠ B=∠ C(等腰三角形的两个底角相等)∵∠ A+ ∠ B+∠ C=180°, ∠ A=50 °
∠B∠A∴底角顶角底角顶角学以致用! (2)等腰三角形的一个底角是70°,
则其顶角是_____________.
(3)如果等腰三角形的一个内角等于70°
那么它的底角度数____________.
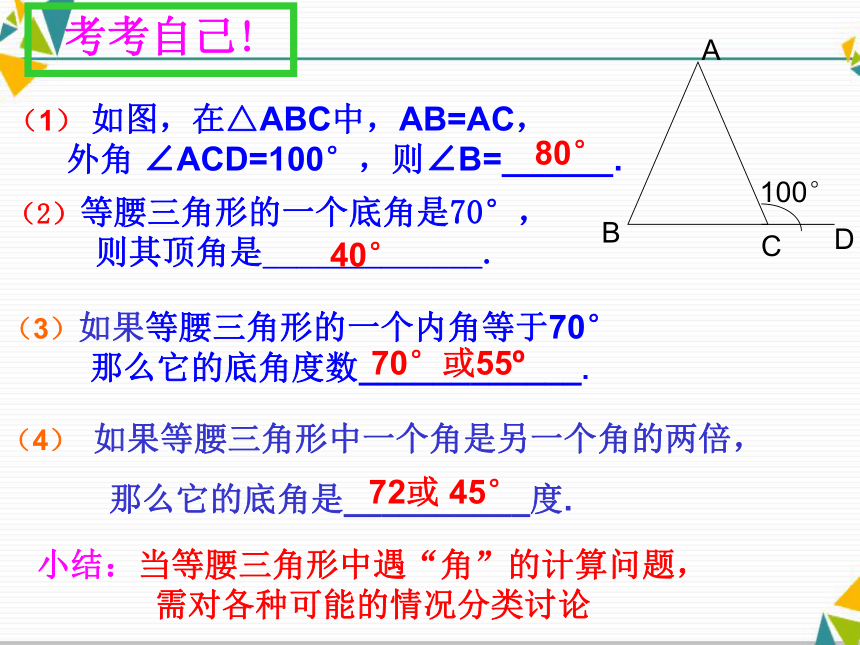
(1) 如图,在△ABC中,AB=AC,
外角 ∠ACD=100°,则∠B=______. (4) 如果等腰三角形中一个角是另一个角的两倍,
那么它的底角是__________度.小结:当等腰三角形中遇“角”的计算问题,
需对各种可能的情况分类讨论80°40°70°或55o72或 45°考考自己! 推论 等边三角形的各角都相等,
并且每一个角都等于60 o
解:∵△ABC是等边三角形
∴AB=BC=AC
∴∠C=∠A=∠B
(同一个三角形中等边对等角) 推论也可以和定理、定义、性质、基本事实
一 样作为推理、论证的依据. ∴∠A=∠B=∠C=180o÷3=60°如何求等边三角形ABC的内角度数?∵∠A+∠B+∠C=180°再探新知!已知△AEF是等边三角形,点B, E,F,C在同一直线上,且BE=EF=FC, 求∠BAC的度数.600600600300300300300及时巩固!“ 等腰三角形
两腰上的中线
_____”
“ 等腰三角形
两腰上的高线 _____ ” “ 等腰三角形
两底角的平分线
相等吗”?
相等 相等再回首!已知: 如图 ,在△ABC中,AB=AC,
BD, CE分别是∠ABC ,∠ACB的平分线。
求证: BD=CE
例2 求证“等腰三角形两底角的平分线相等” 等腰三角形两底角的平分线相等. 已知: 如图 ,在△ABC中,AB=AC,
BD, CE分别是∠ABC ,∠ACB的平分线
求证:BD =CE证明: ∵AB=AC
∴∠ABC=∠ACB∵BD, CE分别是∠ABC ,∠ACB的平分线(等边对等角)∴∠ECB=∠DBC∴?BCE≌ ?CBD(ASA)BD=CE(全等三角形对应边相等)∴∠ECB= ∠ACB, ∠DBC= ∠ABC
等腰三角形底角的平分线相等.如图,在ΔABC中,AB=AC,P为BC的中点,
点D,E分别在 AB ,AC上,AD=AE
求证:PD=PE.
小结:等腰三角形的性质定理------两个底角相等
(或等边对等角)为两个角相等又增加了一种证明方法
强化新知!等腰三角形
的主要特征②从角看-------------①从边看----------③从“三线”看-----------④从整体看---------分类思想 --------在 解决等腰三角形问题中
有着重要 的作用 两边相等两个底角相等
两腰上的中线相等
两腰上的高线相等
两底角平分线相等是轴对称图形
总结、反思! 1. 已知△ABC中,AB=AC,且BC=BF=AF
求∠A 的度数.13解: ∵BF=AF BF=BC
2∵∠3+ ∠ 2+∠C =180° ∵AB=AC ∴∠1 = ∠A ∠ 2= ∠C ∴ ∠ ABC= ∠C∴α+2α+2α=180°设∠A=α则∠1=α ∴∠2=∠1+ ∠A=2α
∠3=2 α-α=α∴ ∠A=α=36° ∠C=∠ABC=2α
(等边对等角)(等边对等角)FF(1) FA=FB
BC=BF
(2) FA=FB
CB=CF(3) FA=FB
FB=FCF结论:∠A=36°∠A= αα2α2α3αα2α2ααα3.从等腰三角形纸片的 底角 顶点出发,将其剪成
两个等腰三角形,求原等腰三角形纸片的顶角度数.
5α=180°7α=180°顶角提示:等腰三角形,遇到边不确定时要分类讨论等腰三角形一条腰上的高与另一条腰的夹角是50°,试求出它顶角的度数. 挑战自己!提示:等腰三角形遇“高线”问题中,要考虑高线在三角形内部和外部两种情形.50°50°顶角140°顶角是40° 1) 等腰三角形一个性质定理:
本节课的我们学习了…… 2)等腰三角形一个推论: 等边三角形的每个内角都等于60° 利用等腰三角形的性质定理
可进行简单的 推理,计算. 4) 分类思想: 在数学解题中起着非常重要的作用.3)两底角相等.
性质定理(1)有__________的三角形
叫做等腰三角形底边
(3)从图形的对称性来说,
等腰三角形是__________图形,
它的对称轴是
_________________________
顶角平分线所在的直线.
(2) 底边和腰相等的等腰三角形
是__________三角形.等边两边相等轴对称回顾旧知! 已知:在△ABC中,AB=AC
求证: ∠ C =∠ BD“等腰三角形的两个底角相等.” 探究新知! 已知:如图,?ABC中, AB=AC
求证:∠C=∠BD证明:作底边BC上的中线AD AB=AC (已知)
AD=AD (公共边)
BD=CD (中线的定义)∴ ?ABD ≌?ACD ∴∠B=∠C (全等三角形
对应角相等)(SSS)在?ABD 和 ?ACD中等腰三角形的两个底角相等.等腰三角形的性质定理1 等腰三角形的两个底角相等.也可以说成 “在同一个三角形中,等边对等角.”
用符号语言可表示为:
在△ABC中
∵ AB=AC
∴ ∠ B=∠ C
运用等腰三角形性质定理可以进行
简单的计算、推理、判断、……..例1 如图,在△ABC中,AB=AC, ∠A =50°,
求∠ B , ∠ C的度数. 解:∵ AB=AC,∴ ∠ B=∠ C(等腰三角形的两个底角相等)∵∠ A+ ∠ B+∠ C=180°, ∠ A=50 °
∠B∠A∴底角顶角底角顶角学以致用! (2)等腰三角形的一个底角是70°,
则其顶角是_____________.
(3)如果等腰三角形的一个内角等于70°
那么它的底角度数____________.
(1) 如图,在△ABC中,AB=AC,
外角 ∠ACD=100°,则∠B=______. (4) 如果等腰三角形中一个角是另一个角的两倍,
那么它的底角是__________度.小结:当等腰三角形中遇“角”的计算问题,
需对各种可能的情况分类讨论80°40°70°或55o72或 45°考考自己! 推论 等边三角形的各角都相等,
并且每一个角都等于60 o
解:∵△ABC是等边三角形
∴AB=BC=AC
∴∠C=∠A=∠B
(同一个三角形中等边对等角) 推论也可以和定理、定义、性质、基本事实
一 样作为推理、论证的依据. ∴∠A=∠B=∠C=180o÷3=60°如何求等边三角形ABC的内角度数?∵∠A+∠B+∠C=180°再探新知!已知△AEF是等边三角形,点B, E,F,C在同一直线上,且BE=EF=FC, 求∠BAC的度数.600600600300300300300及时巩固!“ 等腰三角形
两腰上的中线
_____”
“ 等腰三角形
两腰上的高线 _____ ” “ 等腰三角形
两底角的平分线
相等吗”?
相等 相等再回首!已知: 如图 ,在△ABC中,AB=AC,
BD, CE分别是∠ABC ,∠ACB的平分线。
求证: BD=CE
例2 求证“等腰三角形两底角的平分线相等” 等腰三角形两底角的平分线相等. 已知: 如图 ,在△ABC中,AB=AC,
BD, CE分别是∠ABC ,∠ACB的平分线
求证:BD =CE证明: ∵AB=AC
∴∠ABC=∠ACB∵BD, CE分别是∠ABC ,∠ACB的平分线(等边对等角)∴∠ECB=∠DBC∴?BCE≌ ?CBD(ASA)BD=CE(全等三角形对应边相等)∴∠ECB= ∠ACB, ∠DBC= ∠ABC
等腰三角形底角的平分线相等.如图,在ΔABC中,AB=AC,P为BC的中点,
点D,E分别在 AB ,AC上,AD=AE
求证:PD=PE.
小结:等腰三角形的性质定理------两个底角相等
(或等边对等角)为两个角相等又增加了一种证明方法
强化新知!等腰三角形
的主要特征②从角看-------------①从边看----------③从“三线”看-----------④从整体看---------分类思想 --------在 解决等腰三角形问题中
有着重要 的作用 两边相等两个底角相等
两腰上的中线相等
两腰上的高线相等
两底角平分线相等是轴对称图形
总结、反思! 1. 已知△ABC中,AB=AC,且BC=BF=AF
求∠A 的度数.13解: ∵BF=AF BF=BC
2∵∠3+ ∠ 2+∠C =180° ∵AB=AC ∴∠1 = ∠A ∠ 2= ∠C ∴ ∠ ABC= ∠C∴α+2α+2α=180°设∠A=α则∠1=α ∴∠2=∠1+ ∠A=2α
∠3=2 α-α=α∴ ∠A=α=36° ∠C=∠ABC=2α
(等边对等角)(等边对等角)FF(1) FA=FB
BC=BF
(2) FA=FB
CB=CF(3) FA=FB
FB=FCF结论:∠A=36°∠A= αα2α2α3αα2α2ααα3.从等腰三角形纸片的 底角 顶点出发,将其剪成
两个等腰三角形,求原等腰三角形纸片的顶角度数.
5α=180°7α=180°顶角提示:等腰三角形,遇到边不确定时要分类讨论等腰三角形一条腰上的高与另一条腰的夹角是50°,试求出它顶角的度数. 挑战自己!提示:等腰三角形遇“高线”问题中,要考虑高线在三角形内部和外部两种情形.50°50°顶角140°顶角是40° 1) 等腰三角形一个性质定理:
本节课的我们学习了…… 2)等腰三角形一个推论: 等边三角形的每个内角都等于60° 利用等腰三角形的性质定理
可进行简单的 推理,计算. 4) 分类思想: 在数学解题中起着非常重要的作用.3)两底角相等.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
