浙教数学八上2.6直角三角形课件(22张ppt)
文档属性
| 名称 | 浙教数学八上2.6直角三角形课件(22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 953.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-03 18:30:14 | ||
图片预览






文档简介
课件22张PPT。2.6直角三角形思考:试衣镜的秘密在哪里?2.6 直角三角形(1)你还知道日常生活中常见
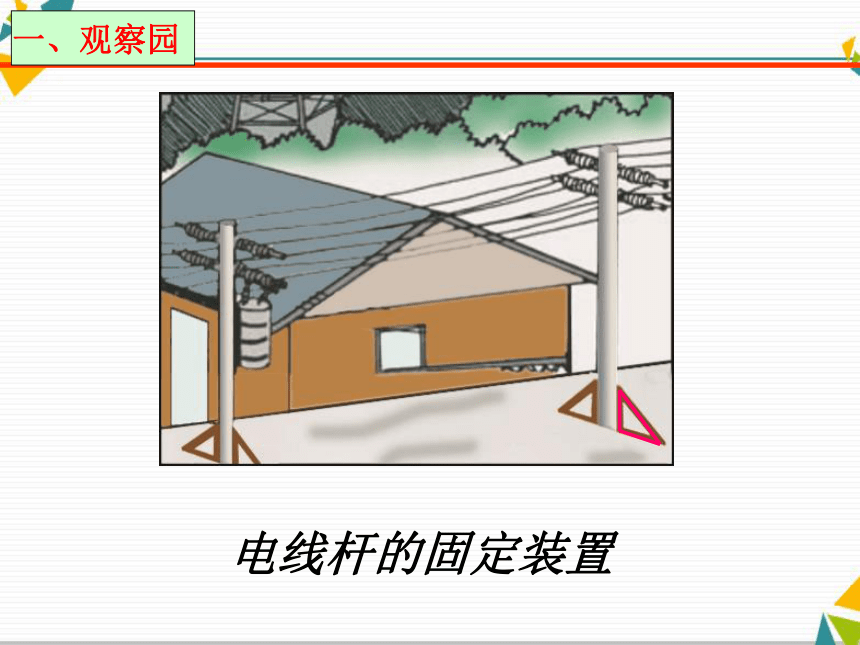
的直角三角形有哪些吗?定义:有一个角是直角的三角形叫做直角三角形.广告牌的支架电线杆的固定装置楼梯的侧面剪一刀,将这个等腰三角形分成两个直角三角形斜边直角∠ADC记为Rt∠ADC直角三角形△ADC
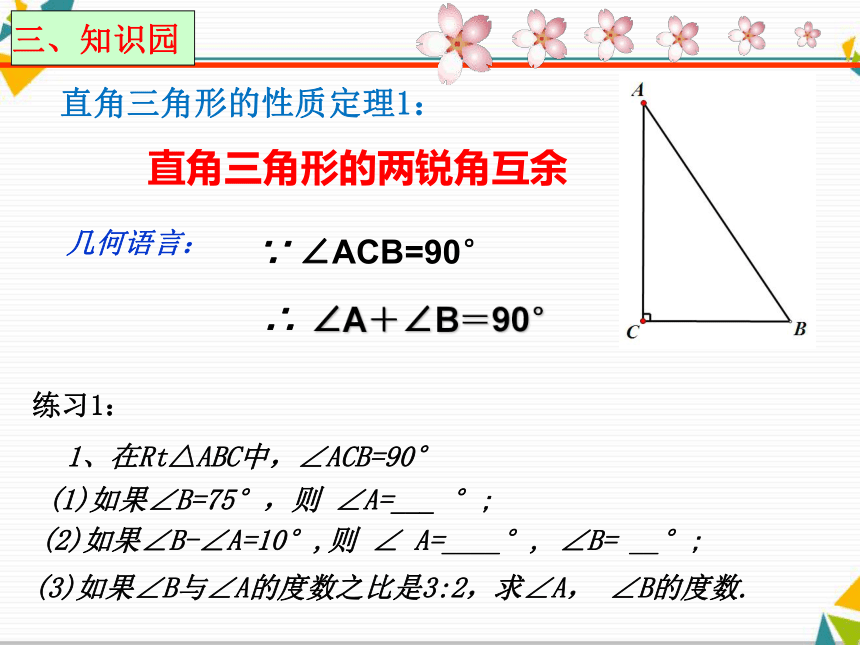
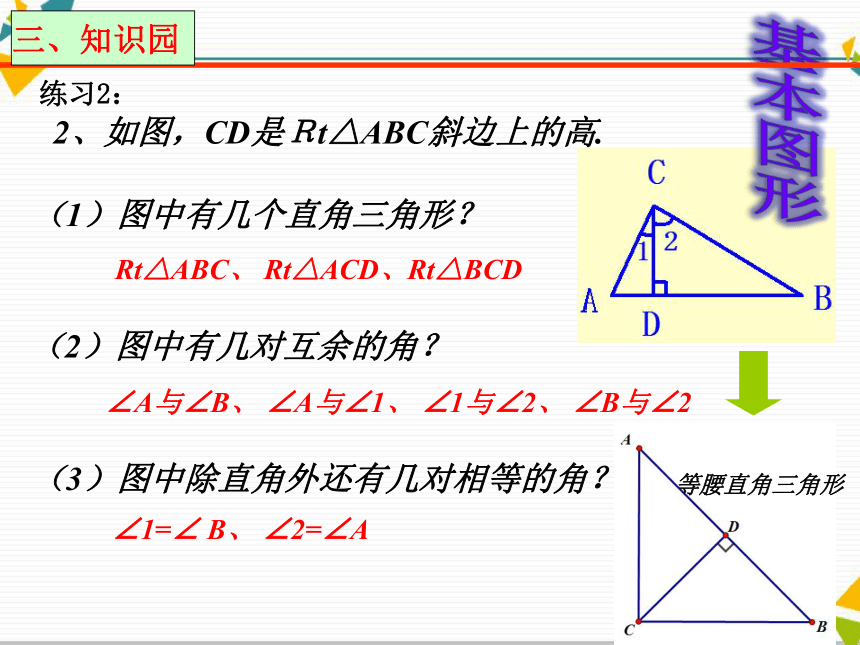
记为Rt△ADC ∠D= 90°∠A+∠C=90°直角三角形的性质定理1:1、在Rt△ABC中,∠ACB=90°(1)如果∠B=75°,则 ∠A=___ °;练习1:(2)如果∠B-∠A=10°,则 ∠ A=____°, ∠B= __°;(3)如果∠B与∠A的度数之比是3:2,求∠A, ∠B的度数.直角三角形的两锐角互余几何语言:∵ ∠ACB=90°∴∠A+∠B=90°2、如图,CD是Rt△ABC斜边上的高.(1)图中有几个直角三角形?Rt△ABC、 Rt△ACD、Rt△BCD(2)图中有几对互余的角?∠A与∠B、 ∠A与∠1、 ∠1与∠2、 ∠B与∠2(3)图中除直角外还有几对相等的角?∠1=∠ B、 ∠2=∠A等腰直角三角形基本图形练习2:思考:如何剪一刀将直角三角形分割成两个等腰三角形。画一个证一个已知:如图,D是Rt△ABC斜边AB上的一点AD=CD, 求证: BD=CD.AD=CDBD=CD已知:如图,D是Rt△ABC斜边AB上的一点,BD=CD.求证: AD=CD.∵ BD=CD(已知),
∴ ∠B=∠DCB (同一三角形,等边对等角).
∵ ∠ACB=90°即∠ACD+∠DCB=90°.
∴ ∠A+ ∠B=90°
(直角三角形的两锐角互余),
∴ ∠A=∠ACD(等角的余角相等),
∴ AD=CD(同一三角形中等角对等边).从本题中,你发现直角三角形斜边上的中线有什么性质?证明: 直角三角形斜边上的中线等于斜边的一半 直角三角形斜边上的中线等于斜边的一半 ∠ACB=90°,D为AB中点注意:1.条件要有双重性2.结论具有多样性条件结论双重性多样性几何语言:或写作∵ ∠ACB=90°,CD是AB边上的中线AD=BD或性质定理2练习3:(1)若AB=10,则AE= , CE= ;(2)若CE=4,则AB= ;∠A+∠2=90°等腰△ACE等腰△BCE∠A+∠B=90°∠1+∠2=90°∠B+∠1=90°∠A=∠1∠B=∠2互余的角:相等的角:相等的线段:基本图形直角三角形斜边上的中线等于斜边的一半2、在Rt△ACB中, ∠ACB=90°,点E是AB边上的中点条件双重性结论多样性(2).直角三角形中斜边上的中线长为10cm,
则斜边长为20cm ( )(3). 如图是一副三角板拼成的四边形ABCD,
E为BD的中点.则EA=EC ( )斜边上中线(条件严密性)练习4:
判断下列语句是否正确,对的打√,错的打× 例2. 如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑行至B。已知AB=200m,问这名滑雪运动员的高度下降了多少m?2、解答类例题你能将本题的结论用一句话归纳概括出性质吗?解:如右图,作Rt△ABC的斜边上的中线CD,则CD=AD= (直角三角形斜边上的中线等于斜边的一半).∵∠B=30° ,∴∠A=90°-∠B=90°-30°=60°(直角三角形两锐角互余).∴△ADC是等边三角形.∴AC=AD=100(m).答:这名滑雪运动员的高度下降了100m.=100(m). 在直角三角形中,
30°角所对的直角边等于斜边的一半。
∵∠ACB=90° ,∠A=30°
∴几何语言:已知:在Rt△ABC与Rt△ACE中,∠ABC=∠AEC=90 °,点M是 AC边上的中点,连结BM、EM、 求证:(1)BM=EM(已知)∵ ∠ ABC= ∠ AEC=90° M是AC边上的中点(已知)(等量代换)(直角三角形斜边上的中线等于斜边的一半)∴ BM= EM(2)∵ BM=EM,P是BE边上的中点(2)MP⊥BE .BE,点P是BE的中点.证明(1)∴ MP ⊥ BE (等腰三角形三线合一)证明:∵ ∠ ABC= ∠ AEC=90 ° M是AC边上的中点∴ BM= EM又∵ P是BE边上的中点(已知)(已知)(等量代换)(直角三角形斜边上的中线等于斜边的一半)变变式1:已知:如图, △ABC和△ACE中, ∠ABC= ∠AEC=Rt ∠,
M是AC边上的中点.连结BM、EM、BE,点P是BE的中点.
求证:MP⊥BE .∴ MP ⊥BE (等腰三角形三线合一)在△ACD中,AE、CB分别是边CD、AD边上的高,M、P分别是AC、BE的中点.
求证:MP⊥BE .证明:∵ ∠AEC= ∠ABC=90 ° M是AC边上的中点∴ ME= MB又∵ P是BE边上的中点∴ MP ⊥ BE (已知)(已知)(等量代换)(直角三角形斜边上的中线等于斜边的一半)(等腰三角形三线合一)连结ME、MB再变变式2:一个定义三个注意点两个性质条件双重性结论多样性有一个角是直角的三角形叫做直角三角形直角三角形的两锐角互余直角三角形斜边上的中线等于斜边的一半条件严密性作业: 一分耕耘,一分收获,相信自己,付出总会有回报。努力吧,成功就在你眼前。老师的赠言谢谢大家!
的直角三角形有哪些吗?定义:有一个角是直角的三角形叫做直角三角形.广告牌的支架电线杆的固定装置楼梯的侧面剪一刀,将这个等腰三角形分成两个直角三角形斜边直角∠ADC记为Rt∠ADC直角三角形△ADC
记为Rt△ADC ∠D= 90°∠A+∠C=90°直角三角形的性质定理1:1、在Rt△ABC中,∠ACB=90°(1)如果∠B=75°,则 ∠A=___ °;练习1:(2)如果∠B-∠A=10°,则 ∠ A=____°, ∠B= __°;(3)如果∠B与∠A的度数之比是3:2,求∠A, ∠B的度数.直角三角形的两锐角互余几何语言:∵ ∠ACB=90°∴∠A+∠B=90°2、如图,CD是Rt△ABC斜边上的高.(1)图中有几个直角三角形?Rt△ABC、 Rt△ACD、Rt△BCD(2)图中有几对互余的角?∠A与∠B、 ∠A与∠1、 ∠1与∠2、 ∠B与∠2(3)图中除直角外还有几对相等的角?∠1=∠ B、 ∠2=∠A等腰直角三角形基本图形练习2:思考:如何剪一刀将直角三角形分割成两个等腰三角形。画一个证一个已知:如图,D是Rt△ABC斜边AB上的一点AD=CD, 求证: BD=CD.AD=CDBD=CD已知:如图,D是Rt△ABC斜边AB上的一点,BD=CD.求证: AD=CD.∵ BD=CD(已知),
∴ ∠B=∠DCB (同一三角形,等边对等角).
∵ ∠ACB=90°即∠ACD+∠DCB=90°.
∴ ∠A+ ∠B=90°
(直角三角形的两锐角互余),
∴ ∠A=∠ACD(等角的余角相等),
∴ AD=CD(同一三角形中等角对等边).从本题中,你发现直角三角形斜边上的中线有什么性质?证明: 直角三角形斜边上的中线等于斜边的一半 直角三角形斜边上的中线等于斜边的一半 ∠ACB=90°,D为AB中点注意:1.条件要有双重性2.结论具有多样性条件结论双重性多样性几何语言:或写作∵ ∠ACB=90°,CD是AB边上的中线AD=BD或性质定理2练习3:(1)若AB=10,则AE= , CE= ;(2)若CE=4,则AB= ;∠A+∠2=90°等腰△ACE等腰△BCE∠A+∠B=90°∠1+∠2=90°∠B+∠1=90°∠A=∠1∠B=∠2互余的角:相等的角:相等的线段:基本图形直角三角形斜边上的中线等于斜边的一半2、在Rt△ACB中, ∠ACB=90°,点E是AB边上的中点条件双重性结论多样性(2).直角三角形中斜边上的中线长为10cm,
则斜边长为20cm ( )(3). 如图是一副三角板拼成的四边形ABCD,
E为BD的中点.则EA=EC ( )斜边上中线(条件严密性)练习4:
判断下列语句是否正确,对的打√,错的打× 例2. 如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑行至B。已知AB=200m,问这名滑雪运动员的高度下降了多少m?2、解答类例题你能将本题的结论用一句话归纳概括出性质吗?解:如右图,作Rt△ABC的斜边上的中线CD,则CD=AD= (直角三角形斜边上的中线等于斜边的一半).∵∠B=30° ,∴∠A=90°-∠B=90°-30°=60°(直角三角形两锐角互余).∴△ADC是等边三角形.∴AC=AD=100(m).答:这名滑雪运动员的高度下降了100m.=100(m). 在直角三角形中,
30°角所对的直角边等于斜边的一半。
∵∠ACB=90° ,∠A=30°
∴几何语言:已知:在Rt△ABC与Rt△ACE中,∠ABC=∠AEC=90 °,点M是 AC边上的中点,连结BM、EM、 求证:(1)BM=EM(已知)∵ ∠ ABC= ∠ AEC=90° M是AC边上的中点(已知)(等量代换)(直角三角形斜边上的中线等于斜边的一半)∴ BM= EM(2)∵ BM=EM,P是BE边上的中点(2)MP⊥BE .BE,点P是BE的中点.证明(1)∴ MP ⊥ BE (等腰三角形三线合一)证明:∵ ∠ ABC= ∠ AEC=90 ° M是AC边上的中点∴ BM= EM又∵ P是BE边上的中点(已知)(已知)(等量代换)(直角三角形斜边上的中线等于斜边的一半)变变式1:已知:如图, △ABC和△ACE中, ∠ABC= ∠AEC=Rt ∠,
M是AC边上的中点.连结BM、EM、BE,点P是BE的中点.
求证:MP⊥BE .∴ MP ⊥BE (等腰三角形三线合一)在△ACD中,AE、CB分别是边CD、AD边上的高,M、P分别是AC、BE的中点.
求证:MP⊥BE .证明:∵ ∠AEC= ∠ABC=90 ° M是AC边上的中点∴ ME= MB又∵ P是BE边上的中点∴ MP ⊥ BE (已知)(已知)(等量代换)(直角三角形斜边上的中线等于斜边的一半)(等腰三角形三线合一)连结ME、MB再变变式2:一个定义三个注意点两个性质条件双重性结论多样性有一个角是直角的三角形叫做直角三角形直角三角形的两锐角互余直角三角形斜边上的中线等于斜边的一半条件严密性作业: 一分耕耘,一分收获,相信自己,付出总会有回报。努力吧,成功就在你眼前。老师的赠言谢谢大家!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
