浙教数学九上3.4圆心角课件(29张ppt)
文档属性
| 名称 | 浙教数学九上3.4圆心角课件(29张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 306.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-03 19:07:14 | ||
图片预览







文档简介
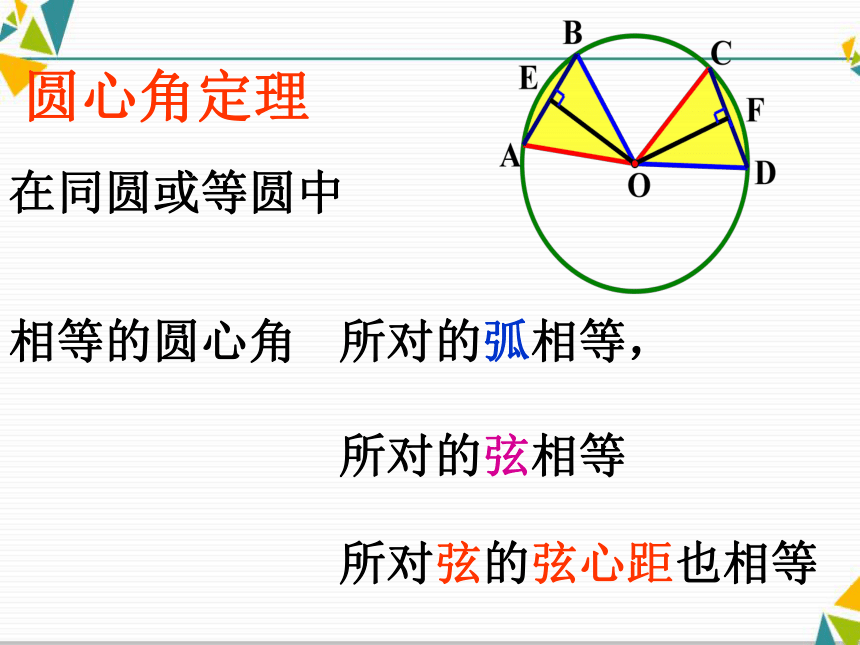
课件29张PPT。 浙教版数学九年级(上)3.4 圆心角温故知新圆心角定理在同圆或等圆中相等的圆心角
所对弦的弦心距也相等 所对的弧相等,
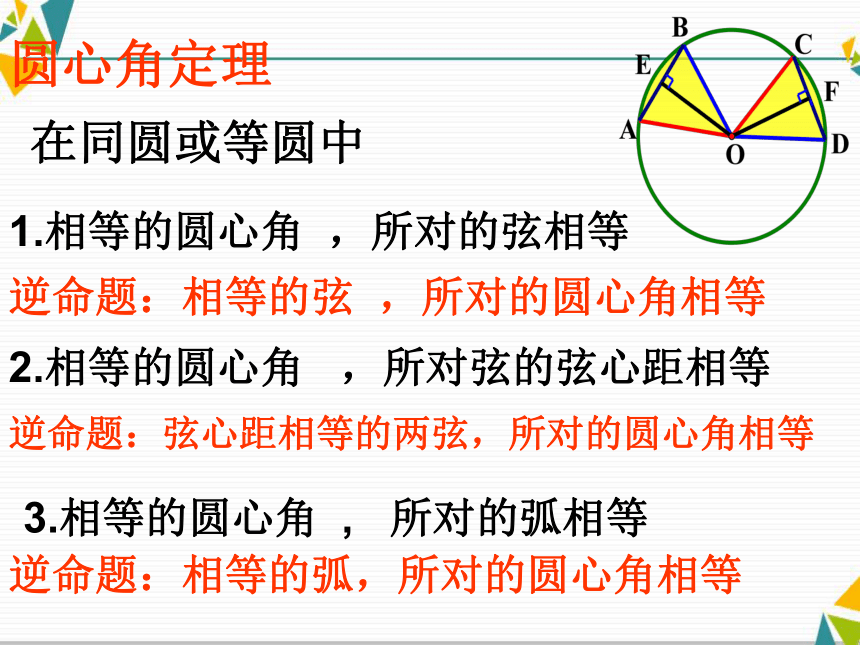
所对的弦相等圆心角定理在同圆或等圆中
1.相等的圆心角 ,所对的弦相等
逆命题:相等的弦 ,所对的圆心角相等
2.相等的圆心角 ,所对弦的弦心距相等逆命题:弦心距相等的两弦,所对的圆心角相等3.相等的圆心角 , 所对的弧相等逆命题:相等的弧,所对的圆心角相等探索知新小组合作与交流第二大组完成第2个逆命题的证明第一大组完成第1个逆命题的证明第三大组完成第3个逆命题的证明探索新知 如图,AB、CD是⊙O的两条弦.OE⊥AB于E,
OF⊥CD于F,逆命题:在同圆或等圆中
相等的弦 , 所对的圆心角相等
探索新知 如图,AB、CD是⊙O的两条弦.OE⊥AB于E,
OF⊥CD于F,逆命题:在同圆或等圆中
弦心距相等的两弦,所对的圆心角相等
探索新知 如图,AB、CD是⊙O的两条弦.OE⊥AB于E,
OF⊥CD于F,逆命题:在同圆或等圆中
相等的弧 , 所对的圆心角相等
如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余的各组量都分别相等。在同圆或等圆中定理运用新知 已知:如图,AB,AC是⊙O的两条弦,OE,OF为AB、AC的弦心距,根据圆心角的相关定理填空:1.填一填如图,已知AB,CD是⊙O 上的两条弦, 求证:AB=CD2.补一补EF 如图,过⊙O上一点P 作两条弦PD、PB,连结OP. 若PO平
分∠BPD. 求证: PB=PD 如图,过⊙O上一点P 作两条弦PD、PB,连结OP. 若PO平
分∠BPD. 求证: PB=PD 如图,过⊙O上一点P 作两条弦PD、PB,连结OP. 若PO平
分∠BPD. 求证: PB=PD 如图,点P在⊙O内,过点P作两条弦AB、CD,连结OP.若PO平分∠BPD. 求证:AB=CD 如图,点P在⊙O内,过点P作两条弦AB、CD,连结OP.若PO平分∠BPD. 求证:AB=CD 如图,点P在⊙O外,过点P
作PB和PD交⊙O于点A和点C.连结
OP,若PO平分∠BPD.求证:AB=CD 如图,点P在⊙O外,过点P
作PB和PD交⊙O于点A和点C.连结
OP,若PO平分∠BPD.求证:AB=CD3.证一证:(2).已知:如图,ΔABC为等边三角形,以
BC直径的 ⊙O分别交AB,AC于点D,E. 4.谈一谈本节课你的收获1.四个元素:圆心角、弦、弧、弦心距2.在同圆或等圆中3 . 在同圆或等圆中
要证明圆心角、弧、弦、弦心距这
四组量中的某一组量相等,通常是转化
成证明另外三组量中的某一组量相等 即一个结论可以通过其余三个条件中的
一个条件来求证或证明5.找一找相等的角相等的弧相等的线段5.找一找相
等
的
角1.∠ABC=∠BAC=∠ACB=
∠BOD=∠COD=60°2.∠AOB=∠BOC=∠AOC=120°4.∠APB=∠APC=90°3.∠BAD=∠CAD=∠ABO=
∠OBC=∠OCB=∠ACO=30°5.找一找相
等
的
弧5.找一找相
等
的
线
段1.AB=BC=AC2.OA=OB=OC=OD3.BP=PC4.OP=PD连结BD,CD.5.找一找问题1:四边形BDCO是菱形吗?
如果是,你能证明吗?问题2:若⊙O的半径为r, 你能求
出等边三角形ABC的边长吗?问题3:若等边三角形ABC的边长a,
你还能求出⊙O的半径吗?ra选做:全效学习3.4圆心角(2)B组
必做:作业本3.4圆心角(2)
作业
所对弦的弦心距也相等 所对的弧相等,
所对的弦相等圆心角定理在同圆或等圆中
1.相等的圆心角 ,所对的弦相等
逆命题:相等的弦 ,所对的圆心角相等
2.相等的圆心角 ,所对弦的弦心距相等逆命题:弦心距相等的两弦,所对的圆心角相等3.相等的圆心角 , 所对的弧相等逆命题:相等的弧,所对的圆心角相等探索知新小组合作与交流第二大组完成第2个逆命题的证明第一大组完成第1个逆命题的证明第三大组完成第3个逆命题的证明探索新知 如图,AB、CD是⊙O的两条弦.OE⊥AB于E,
OF⊥CD于F,逆命题:在同圆或等圆中
相等的弦 , 所对的圆心角相等
探索新知 如图,AB、CD是⊙O的两条弦.OE⊥AB于E,
OF⊥CD于F,逆命题:在同圆或等圆中
弦心距相等的两弦,所对的圆心角相等
探索新知 如图,AB、CD是⊙O的两条弦.OE⊥AB于E,
OF⊥CD于F,逆命题:在同圆或等圆中
相等的弧 , 所对的圆心角相等
如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余的各组量都分别相等。在同圆或等圆中定理运用新知 已知:如图,AB,AC是⊙O的两条弦,OE,OF为AB、AC的弦心距,根据圆心角的相关定理填空:1.填一填如图,已知AB,CD是⊙O 上的两条弦, 求证:AB=CD2.补一补EF 如图,过⊙O上一点P 作两条弦PD、PB,连结OP. 若PO平
分∠BPD. 求证: PB=PD 如图,过⊙O上一点P 作两条弦PD、PB,连结OP. 若PO平
分∠BPD. 求证: PB=PD 如图,过⊙O上一点P 作两条弦PD、PB,连结OP. 若PO平
分∠BPD. 求证: PB=PD 如图,点P在⊙O内,过点P作两条弦AB、CD,连结OP.若PO平分∠BPD. 求证:AB=CD 如图,点P在⊙O内,过点P作两条弦AB、CD,连结OP.若PO平分∠BPD. 求证:AB=CD 如图,点P在⊙O外,过点P
作PB和PD交⊙O于点A和点C.连结
OP,若PO平分∠BPD.求证:AB=CD 如图,点P在⊙O外,过点P
作PB和PD交⊙O于点A和点C.连结
OP,若PO平分∠BPD.求证:AB=CD3.证一证:(2).已知:如图,ΔABC为等边三角形,以
BC直径的 ⊙O分别交AB,AC于点D,E. 4.谈一谈本节课你的收获1.四个元素:圆心角、弦、弧、弦心距2.在同圆或等圆中3 . 在同圆或等圆中
要证明圆心角、弧、弦、弦心距这
四组量中的某一组量相等,通常是转化
成证明另外三组量中的某一组量相等 即一个结论可以通过其余三个条件中的
一个条件来求证或证明5.找一找相等的角相等的弧相等的线段5.找一找相
等
的
角1.∠ABC=∠BAC=∠ACB=
∠BOD=∠COD=60°2.∠AOB=∠BOC=∠AOC=120°4.∠APB=∠APC=90°3.∠BAD=∠CAD=∠ABO=
∠OBC=∠OCB=∠ACO=30°5.找一找相
等
的
弧5.找一找相
等
的
线
段1.AB=BC=AC2.OA=OB=OC=OD3.BP=PC4.OP=PD连结BD,CD.5.找一找问题1:四边形BDCO是菱形吗?
如果是,你能证明吗?问题2:若⊙O的半径为r, 你能求
出等边三角形ABC的边长吗?问题3:若等边三角形ABC的边长a,
你还能求出⊙O的半径吗?ra选做:全效学习3.4圆心角(2)B组
必做:作业本3.4圆心角(2)
作业
同课章节目录
