浙教数学九上2.2简单事件的概率课件(16张ppt)
文档属性
| 名称 | 浙教数学九上2.2简单事件的概率课件(16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 389.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-04 10:47:58 | ||
图片预览





文档简介
课件16张PPT。2.1 简单事件的概率复习引入 必然事件;
在一定条件下必然发生的事件,
不可能事件;
在一定条件下不可能发生的事件
随机事件;
在一定条件下可能发生也可能不发生的事件,2.概率的定义事件发生可能性的大小称为事件发生的概率。事件A的概率,记作P(A).0≤P(A) ≤1.
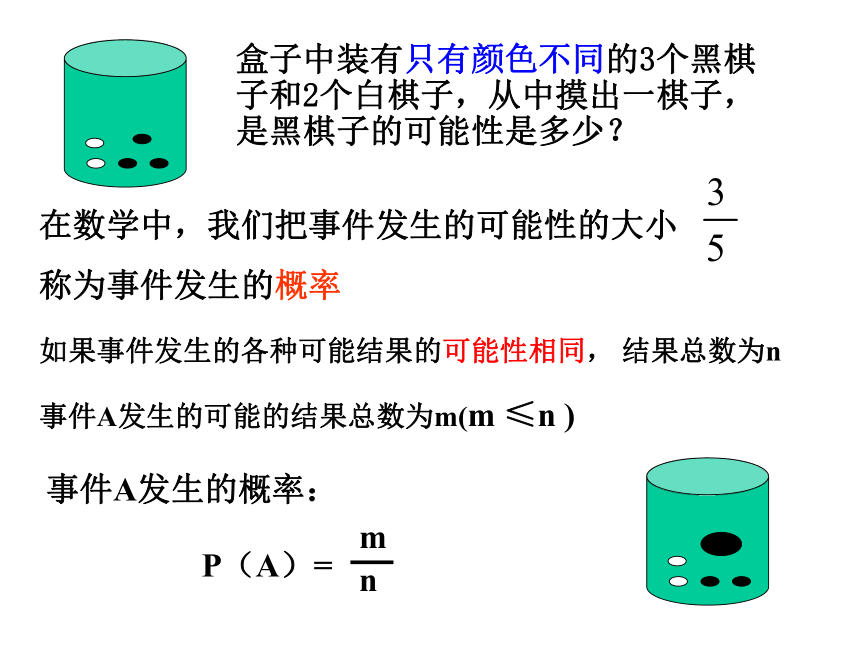
必然事件的概率是1,不可能事件的概率是0.盒子中装有只有颜色不同的3个黑棋子和2个白棋子,从中摸出一棋子,是黑棋子的可能性是多少?在数学中,我们把事件发生的可能性的大小
称为事件发生的概率如果事件发生的各种可能结果的可能性相同,事件A发生的可能的结果总数为m(m ≤n )结果总数为n事件A发生的概率:1、如图 三色转盘,每个扇形的圆心角度数相等,让转盘自由转动一次, “指针落在黄色区域”的概率是多少?“指针落在红色区域”的概率是多少?
“指针落在蓝色区域”的概率是多少?热身练习: 2、 如图是一个转盘,分成7个相同的扇形,颜色分为红、绿、黄三种颜色,指针的位置固定,转动转盘后任其自由停止.其中的某个扇形会恰好停在指针的位置(如果指针指向两扇形交线时,当作指向右边的扇形),求下列事件的概率:(1) 指针指向红色;解:按颜色把7个扇形分别记为:红1,红2,红3,绿1,绿2,黄1,黄2,
所有可能结果共7种.
(1)指针指向红色的结果有3个,即红1,红2,红3,
∴P(指向红色)=3/7;解:(2)指针指向红色或黄色的结果有5个,即红1,红2,红3,黄1,黄2,
∴P(指向红色或黄色)=5/7;
(2)指针指向红色或黄色;(3)指针不指向红色.(3) 指针不指向红的结果有4个,即黄1,黄2,绿1,绿2,
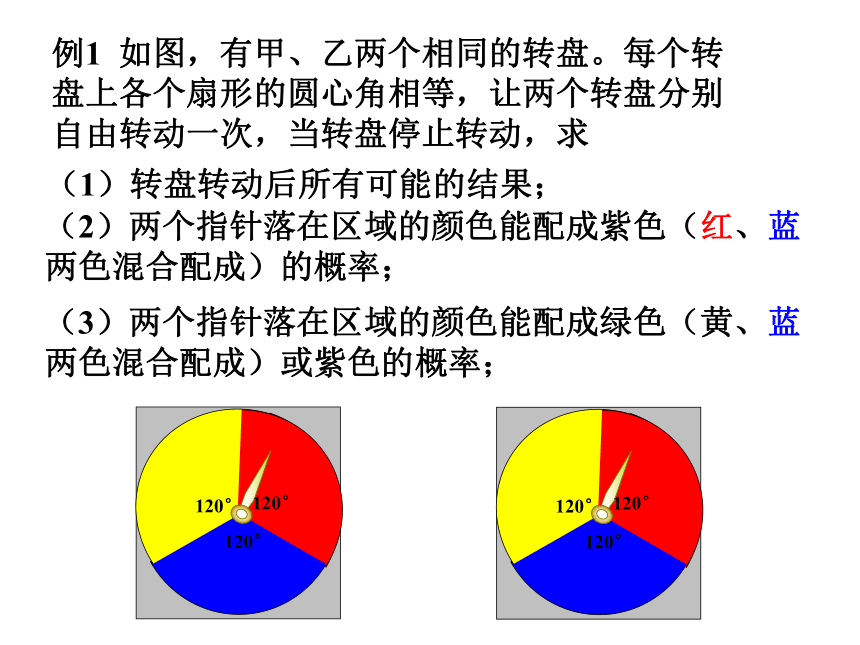
∴P(不指向红色)=4/7.例1 如图,有甲、乙两个相同的转盘。每个转盘上各个扇形的圆心角相等,让两个转盘分别自由转动一次,当转盘停止转动,求(1)转盘转动后所有可能的结果;(2)两个指针落在区域的颜色能配成紫色(红、蓝两色混合配成)的概率;(3)两个指针落在区域的颜色能配成绿色(黄、蓝两色混合配成)或紫色的概率;例2 一个盒子里装有4个只有颜色不同的球,其中3个红球,1个白球。从盒子里摸出一个球,记下颜色后放回,并搅匀,再摸出一个球。(2)摸出一个红球,一个白球的概率;(3)摸出2个红球的概率;不放回第1次第2次(1)写出两次摸球的所有可能的结果;创新实践 巩固新知 1、袋子里装有红、黄、蓝三种小球,其形状、大小、质量、质地等完全相同,每种颜色的小球5个,且分别标有数字1,2,3,4,5现从中摸出一球:
(1)摸出的球是蓝色球的概率为多少?
(2)摸出的球是5号球的概率为多少?
(3)摸出的球是红色1号球的概率为多少? 解: (1) 按颜色和标有数字将15个球分别记作红1,红2红3,红4,红5,黄1,黄2,黄3,黄4,黄5,蓝1, 蓝2,蓝3,蓝4,蓝5,共有15种可能性相等的结果.而 摸出的球是蓝色球包含其中5种结果,即:蓝1,蓝2
蓝3,蓝4,蓝5.
∴P(摸出蓝色球)=5/15=1/3 .2、任意把骰子连续抛掷两次,(3)朝上一面的点数相同的概率;(4)朝上一面的点数都为偶数的概率;(5)两次朝上一面的点数的和为5的概率(2)朝上一面的点数一次为3,一次为4的概率;(1)写出抛掷后的所有可能的结果; 3.小明和小刚改用如图所示的两个转盘进行“配紫色”游戏.配成紫色,小刚得1分,否则小明得1分.这个游戏对双方公平吗?为什么?
4、小明和小刚正在做掷骰子的游戏.两人各掷一枚子. (1)当两枚骰子的点数之和为奇数时,小刚得1分,否则小明得1分.这个游戏对双方公平吗? 游戏怎样才算公平?每人获胜的概率是多少? (2)当两枚骰子的点数之积为奇数时,小刚得1分,否则小明得1分.这个游戏对双方公平吗?为什么?5.在一个不透明的袋中装有除颜色外其余都相同的3个小球,其中一个红色球、两个黄色球.如果第一次先从袋中摸出一个球后不再放回,第二次再从袋中摸出一个,那么两次都摸到黄色球的概率是 _____.开始红黄黄(红,黄)黄黄红黄红(黄,黄)(黄,红)(黄,黄)(黄,红)黄(红,黄)如果事件发生的各种可能结果的可能性相同,事件A发生的可能的结果总数为m那么事件A发生的概率为把事件发生的可能性的大小称为事件发生的概率结果总数为n教学小结:用树状图或表格表示概率回 味 无 穷 1、利用树状图或表格可以清晰地表
示出某个事件发生的所有可能出现的
结果;从而较方便地求出某些事件发
生的概率.2 根据不同的情况选择恰当的方法表示某个事件发生的所有可能结果。
在一定条件下必然发生的事件,
不可能事件;
在一定条件下不可能发生的事件
随机事件;
在一定条件下可能发生也可能不发生的事件,2.概率的定义事件发生可能性的大小称为事件发生的概率。事件A的概率,记作P(A).0≤P(A) ≤1.
必然事件的概率是1,不可能事件的概率是0.盒子中装有只有颜色不同的3个黑棋子和2个白棋子,从中摸出一棋子,是黑棋子的可能性是多少?在数学中,我们把事件发生的可能性的大小
称为事件发生的概率如果事件发生的各种可能结果的可能性相同,事件A发生的可能的结果总数为m(m ≤n )结果总数为n事件A发生的概率:1、如图 三色转盘,每个扇形的圆心角度数相等,让转盘自由转动一次, “指针落在黄色区域”的概率是多少?“指针落在红色区域”的概率是多少?
“指针落在蓝色区域”的概率是多少?热身练习: 2、 如图是一个转盘,分成7个相同的扇形,颜色分为红、绿、黄三种颜色,指针的位置固定,转动转盘后任其自由停止.其中的某个扇形会恰好停在指针的位置(如果指针指向两扇形交线时,当作指向右边的扇形),求下列事件的概率:(1) 指针指向红色;解:按颜色把7个扇形分别记为:红1,红2,红3,绿1,绿2,黄1,黄2,
所有可能结果共7种.
(1)指针指向红色的结果有3个,即红1,红2,红3,
∴P(指向红色)=3/7;解:(2)指针指向红色或黄色的结果有5个,即红1,红2,红3,黄1,黄2,
∴P(指向红色或黄色)=5/7;
(2)指针指向红色或黄色;(3)指针不指向红色.(3) 指针不指向红的结果有4个,即黄1,黄2,绿1,绿2,
∴P(不指向红色)=4/7.例1 如图,有甲、乙两个相同的转盘。每个转盘上各个扇形的圆心角相等,让两个转盘分别自由转动一次,当转盘停止转动,求(1)转盘转动后所有可能的结果;(2)两个指针落在区域的颜色能配成紫色(红、蓝两色混合配成)的概率;(3)两个指针落在区域的颜色能配成绿色(黄、蓝两色混合配成)或紫色的概率;例2 一个盒子里装有4个只有颜色不同的球,其中3个红球,1个白球。从盒子里摸出一个球,记下颜色后放回,并搅匀,再摸出一个球。(2)摸出一个红球,一个白球的概率;(3)摸出2个红球的概率;不放回第1次第2次(1)写出两次摸球的所有可能的结果;创新实践 巩固新知 1、袋子里装有红、黄、蓝三种小球,其形状、大小、质量、质地等完全相同,每种颜色的小球5个,且分别标有数字1,2,3,4,5现从中摸出一球:
(1)摸出的球是蓝色球的概率为多少?
(2)摸出的球是5号球的概率为多少?
(3)摸出的球是红色1号球的概率为多少? 解: (1) 按颜色和标有数字将15个球分别记作红1,红2红3,红4,红5,黄1,黄2,黄3,黄4,黄5,蓝1, 蓝2,蓝3,蓝4,蓝5,共有15种可能性相等的结果.而 摸出的球是蓝色球包含其中5种结果,即:蓝1,蓝2
蓝3,蓝4,蓝5.
∴P(摸出蓝色球)=5/15=1/3 .2、任意把骰子连续抛掷两次,(3)朝上一面的点数相同的概率;(4)朝上一面的点数都为偶数的概率;(5)两次朝上一面的点数的和为5的概率(2)朝上一面的点数一次为3,一次为4的概率;(1)写出抛掷后的所有可能的结果; 3.小明和小刚改用如图所示的两个转盘进行“配紫色”游戏.配成紫色,小刚得1分,否则小明得1分.这个游戏对双方公平吗?为什么?
4、小明和小刚正在做掷骰子的游戏.两人各掷一枚子. (1)当两枚骰子的点数之和为奇数时,小刚得1分,否则小明得1分.这个游戏对双方公平吗? 游戏怎样才算公平?每人获胜的概率是多少? (2)当两枚骰子的点数之积为奇数时,小刚得1分,否则小明得1分.这个游戏对双方公平吗?为什么?5.在一个不透明的袋中装有除颜色外其余都相同的3个小球,其中一个红色球、两个黄色球.如果第一次先从袋中摸出一个球后不再放回,第二次再从袋中摸出一个,那么两次都摸到黄色球的概率是 _____.开始红黄黄(红,黄)黄黄红黄红(黄,黄)(黄,红)(黄,黄)(黄,红)黄(红,黄)如果事件发生的各种可能结果的可能性相同,事件A发生的可能的结果总数为m那么事件A发生的概率为把事件发生的可能性的大小称为事件发生的概率结果总数为n教学小结:用树状图或表格表示概率回 味 无 穷 1、利用树状图或表格可以清晰地表
示出某个事件发生的所有可能出现的
结果;从而较方便地求出某些事件发
生的概率.2 根据不同的情况选择恰当的方法表示某个事件发生的所有可能结果。
同课章节目录
