浙教数学九上3.3垂径定理课件(14张ppt)
文档属性
| 名称 | 浙教数学九上3.3垂径定理课件(14张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-04 00:00:00 | ||
图片预览




文档简介
课件14张PPT。3.3垂径定理知识回顾
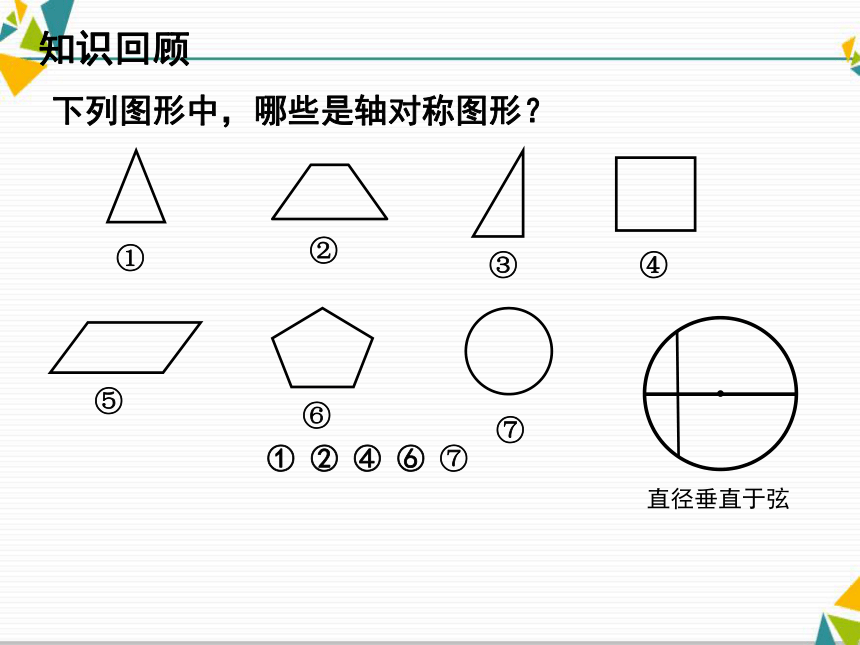
下列图形中,哪些是轴对称图形? ①②③④⑤⑥① ② ④ ⑥ ⑦⑦直径垂直于弦合作学习 在透明纸上任意作一个圆和这个圆的一条弦AB,再作一条和弦AB垂直的直径CD,CD和AB相交于点E.然后沿着直径CD所在的直线把纸折叠.
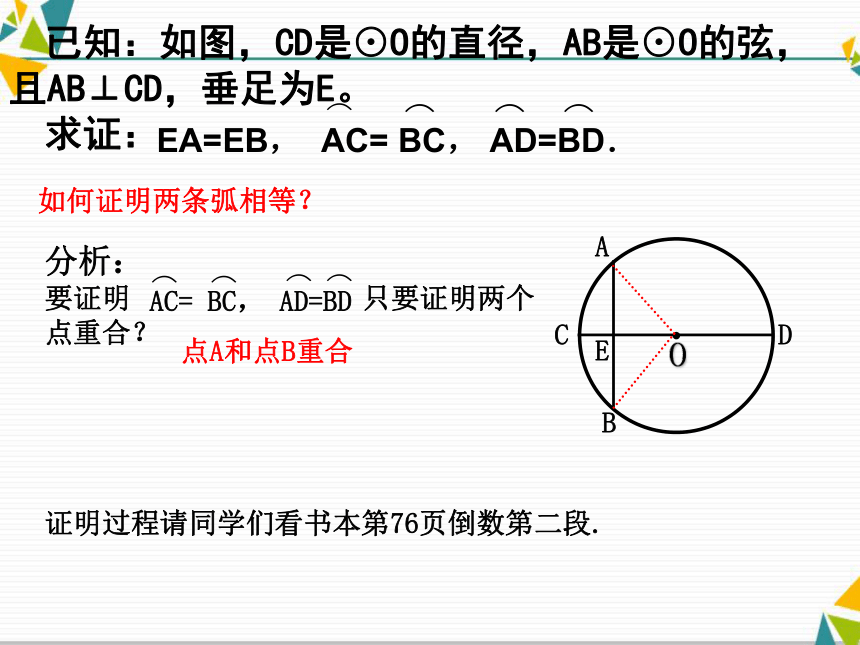
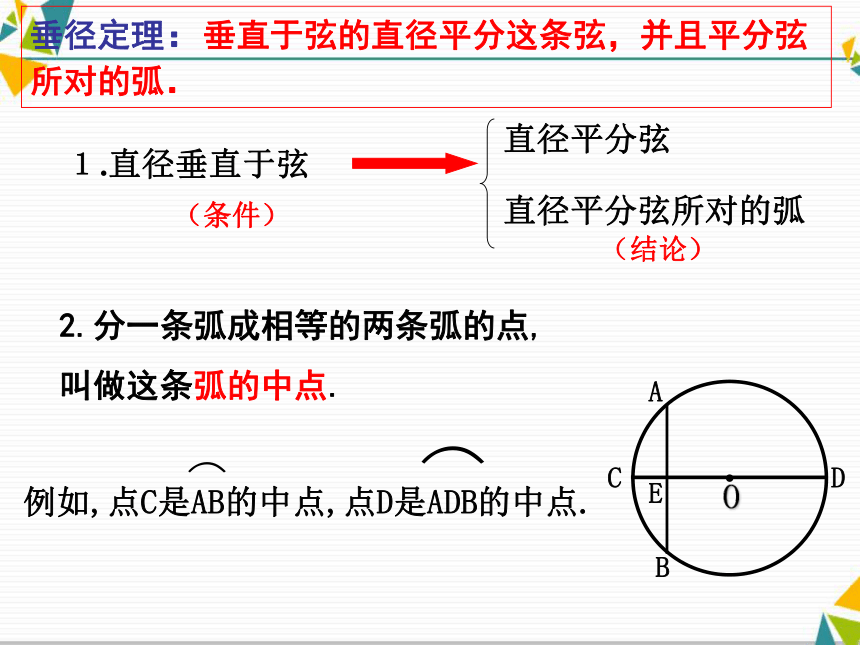
(1)你发现哪些点、线段、圆弧互相重合?(小组交流结果)(2)你发现有哪些线段、圆弧相等?(小组交流结果)(3)你能证明你发现的结论吗?(四人小组讨论)如何证明两条弧相等?证明过程请同学们看书本第76页倒数第二段.点A和点B重合垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.1.直径垂直于弦直径平分弦所对的弧直径平分弦2.分一条弧成相等的两条弧的点,
叫做这条弧的中点.
(条件)(结论)在下列图形中,能使用垂径定理的图形有哪些? 辩一辩不能不能能能能能D作法:⒈ 连结AB.⒉ 作AB的垂直平分线 CD,交弧AB于点E.点E就是所求弧AB的中点.CDABE变式: 求弧AB的四等分点.应用1:利用垂径定理作已知弧的中点强调:
等分弧时一定要作弧所对的弦的垂直平分线.错误正确例2 一条排水管的截面如图所示.排水管的半径OB=10,水面宽AB=16,求截面圆心O到水面的距离 .BC应用2:垂径定理的有关计算1.圆心到圆的一条弦的距离叫做弦心距.rd题后小结2.作弦心距和半径是圆中常见的辅助线.一条排水管的截面如图所示.变式(1)1.已知圆心O到水面的距离OC =6,半径OB=10,
求水面宽AB.2.已知圆心O到水面的距离OC =6,水面宽AB=16,
求半径OB.D3.一条排水管的截面如图所示.排水管的半径OB=10,水面宽AB=16,求管内水面的最大深度CD.x10-x108变式(2)变式(3)
已知:如图,若以O为圆心作一个⊙O的同心圆,交大圆的弦AB于C,D两点.
求证:AC=BD.
E(1)圆的轴对称性;(2)垂径定理; (3)垂径定理的应用3.解题的主要方法:课堂小结(2)画弦心距和半径是圆中常见的辅助线;2.应用垂径定理要注意哪些问题?(1)在圆有关的问题时,常常构造直角三角形,
利用垂径定理和勾股定理相结合的方法来解决。 1.这节课我们主要学了哪些内容?(3)方程思想;作业布置:(课本P78作业题)
1.必做题:1,2,3,4题
2.选做题:5,6题
课后思考题:第7题
下列图形中,哪些是轴对称图形? ①②③④⑤⑥① ② ④ ⑥ ⑦⑦直径垂直于弦合作学习 在透明纸上任意作一个圆和这个圆的一条弦AB,再作一条和弦AB垂直的直径CD,CD和AB相交于点E.然后沿着直径CD所在的直线把纸折叠.
(1)你发现哪些点、线段、圆弧互相重合?(小组交流结果)(2)你发现有哪些线段、圆弧相等?(小组交流结果)(3)你能证明你发现的结论吗?(四人小组讨论)如何证明两条弧相等?证明过程请同学们看书本第76页倒数第二段.点A和点B重合垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.1.直径垂直于弦直径平分弦所对的弧直径平分弦2.分一条弧成相等的两条弧的点,
叫做这条弧的中点.
(条件)(结论)在下列图形中,能使用垂径定理的图形有哪些? 辩一辩不能不能能能能能D作法:⒈ 连结AB.⒉ 作AB的垂直平分线 CD,交弧AB于点E.点E就是所求弧AB的中点.CDABE变式: 求弧AB的四等分点.应用1:利用垂径定理作已知弧的中点强调:
等分弧时一定要作弧所对的弦的垂直平分线.错误正确例2 一条排水管的截面如图所示.排水管的半径OB=10,水面宽AB=16,求截面圆心O到水面的距离 .BC应用2:垂径定理的有关计算1.圆心到圆的一条弦的距离叫做弦心距.rd题后小结2.作弦心距和半径是圆中常见的辅助线.一条排水管的截面如图所示.变式(1)1.已知圆心O到水面的距离OC =6,半径OB=10,
求水面宽AB.2.已知圆心O到水面的距离OC =6,水面宽AB=16,
求半径OB.D3.一条排水管的截面如图所示.排水管的半径OB=10,水面宽AB=16,求管内水面的最大深度CD.x10-x108变式(2)变式(3)
已知:如图,若以O为圆心作一个⊙O的同心圆,交大圆的弦AB于C,D两点.
求证:AC=BD.
E(1)圆的轴对称性;(2)垂径定理; (3)垂径定理的应用3.解题的主要方法:课堂小结(2)画弦心距和半径是圆中常见的辅助线;2.应用垂径定理要注意哪些问题?(1)在圆有关的问题时,常常构造直角三角形,
利用垂径定理和勾股定理相结合的方法来解决。 1.这节课我们主要学了哪些内容?(3)方程思想;作业布置:(课本P78作业题)
1.必做题:1,2,3,4题
2.选做题:5,6题
课后思考题:第7题
同课章节目录
