浙教版九年级数学上册1.1二次函数课件(26张ppt)
文档属性
| 名称 | 浙教版九年级数学上册1.1二次函数课件(26张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 43.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-01 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
1.1 二次函数
1、什么叫函数?
在某变化过程中的两个变量x、y,当变量x在某个范围内取一个确定的值,另一个变量y总有唯一的值与它对应。
这样的两个变量之间的关系我们把它叫做函数关系。
对于上述变量x 、y,我们把y叫x的函数。 x叫自变量, y叫应变量。
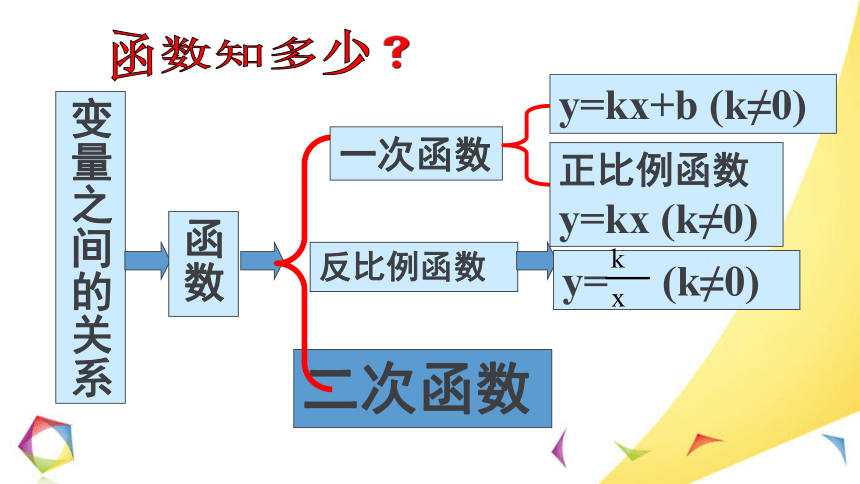
目前,我们已经学习了那几种类型的函数?
知识回顾
二次函数
问题:如图,从喷头喷出的水珠,在空中走过一条曲线后落到池中央,在这条曲线的各个位置上,水珠的竖直高度h与它距离喷头的水平距离x之间有什么关系?
上面问题中变量之间的关系可以用哪一种函数来表示?这种函数与以前学习的函数、方程有哪些联系?
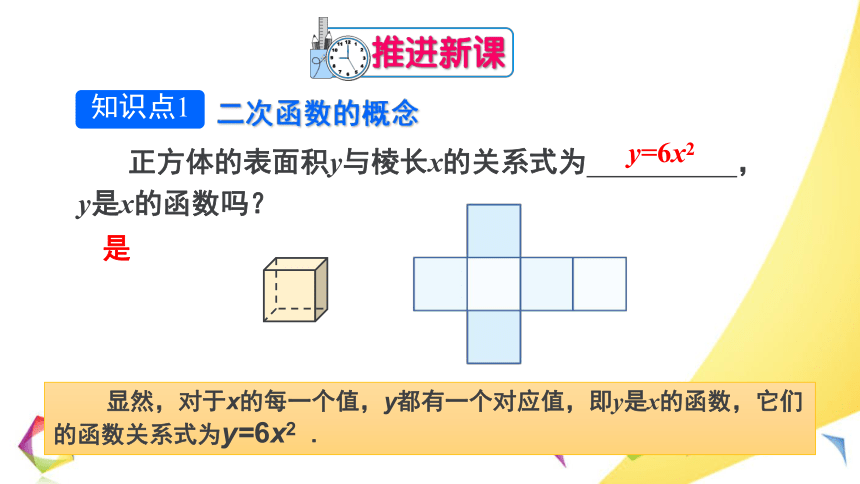
正方体的表面积y与棱长x的关系式为 ,y是x的函数吗?
知识点1
二次函数的概念
y=6x2
是
显然,对于x的每一个值,y都有一个对应值,即y是x的函数,它们的函数关系式为y=6x2 .
我们再来看几个问题。
问题1 n个球队参加比赛,每两队之间进行一场比赛。比赛的场次数m与球队数n有什么关系?
即,
m是n的函数吗?
某种产品现在的年产量为20t,计划今后两年增加产量。如果每年都比上一年的产量增加x倍,那么两年后这种产品的年产量y将随计划所定的x值而确定,y与x之间的关系应怎样表示?
问题2
产品原产量是20t,一年后的产量是原产量的 倍;再经过一年后的产量是一年后的产量的 倍.于是两年后的产量y与增加的倍数x的关系式为 .
(1+x)
(1+x)
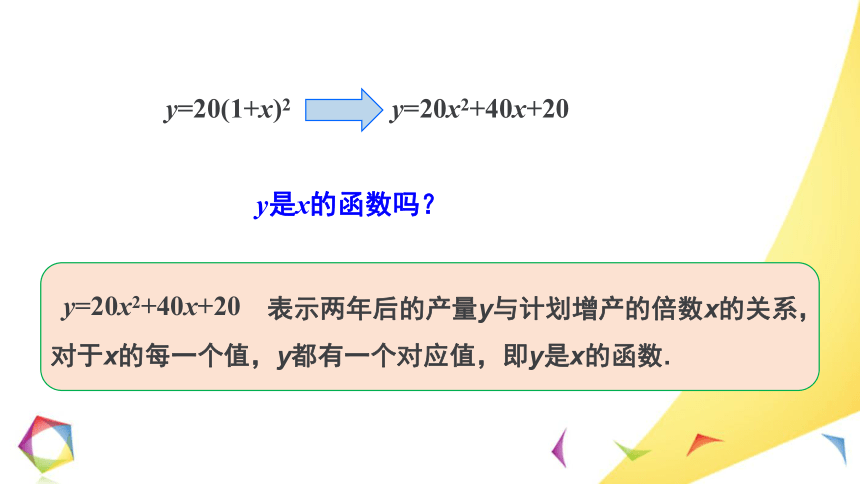
y=20(1+x)2
y是x的函数吗?
y=20(1+x)2
y=20x2+40x+20
上述三个函数都是用自变量的二次式表示的。一般地,形如y=ax?+bx+c(a,b,c为常数,a≠0)
的函数,叫做二次函数。其中x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项。
二次项
一次项
常数项
二次函数的一般形式:
y=ax2+bx+c (其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时, y=ax2+c
当c=0时, y=ax2+bx
当b=0,c=0时, y=ax2
①y=6x2 ,
分别指出下列二次函数解析式的自变量、各项及各项系数。
出题角度一 二次函数的识别
下列函数中是二次函数的有 。
二次函数:y=ax?+bx+c
(a,b,c为常数,a≠0)
√
a=0
×
最高次数是4
×
×
√
①⑤
运用定义法判断一个函数是否为二次函数的步骤:
(1)将函数解析式右边整理为含自变量的代数式,左边是函数(因变量)的形式;
(2)判断右边含自变量的代数式是否是整式;
(3)判断自变量的最高次数是否是2;
(4)判断二次项系数是否不等于0.
出题角度二 应用二次函数的概念求相关字母的取值(或范围)
解:
根据二次函数的定义可得
解得m=3或m=-1.
当m=3时,y=6x2+9;当m=-1时,y=2x2-4x+1.
综上所述,该二次函数的解析式为:
y=6x2+9或y=2x2-4x+1.
练习
解:依题意,得
解得a=-1.
出题角度三 求二次函数的函数值
知识点2
根据具体问题确定二次函数解析式
①已知圆的面积y(cm2)与圆的半径x(cm),写出y与x之间的函数关系式;
②王先生存入银行2万元,先存一个一年定期,一年后银行将本息自动转存为又一个一年定期,设一年定期的存款年利率为x,两年后王先生共得本息和y万元,写出y与x之间的函数关系式;
③一个圆柱的高等于底面半径,写出它的表面积S与半径r之间的关系式.
y=πx2
y=2(1+x)2
S=4πr2
做一做:
(x>0)
(x>0)
(r>0)
说一说以上二次函数解析式的各项系数。
(2)设铺设地面所用瓷砖的总块数为y,请写出y与n的函数关系式
4.如图,用同样规格的正方形白色瓷砖铺设矩形地面,请观察下列图形并解答有关问题:
n=1
n=2
n=3
(1)在第n个图形中,每一横行共有 块瓷砖,每一竖列共有 块瓷砖(均用含n的代数式表示);
(n+3)
(n+2)
y=(n+3)(n+2)即 y=n?+5n+6
1. 下列函数是二次函数的是( )
A.y=2x+1 B.y=-2x+1 C.y=x2+2 D.y= x-2
2. 二次函数y=3x2-2x-4的二次项系数与常数项的和是( )
A.1 B.-1 C.7 D.-6
3.已知函数y=(a-1)x2+3x-1,若y是x的二次函数,则a的取值范围是 .
C
基础巩固
B
a≠1
4.某种商品的价格是2元,准备进行两次降价,如果每次降价的百分率都是x,则经过两次降价后的价格y(单位:元)与每次降价的百分率x的函数关系式是 .
5. 正方形的边长为10cm,在中间挖去一个边长为xcm的正方形,若剩余部分的面积为ycm2,则y与x的函数关系式是y=100-x2,x的取值范围为 .
6. 一辆汽车的行驶距离s(单位:m)与行驶时间t(单位:s)的函数关系式为s=9t+12t2,则经过12s汽车行驶了 m,行驶380m 需 s.
y=2(1-x)2
0≤x≤10
180
20
综合应用
7.如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,写出△PBQ的面积S与出发时间t(s)的函数关系式及t的取值范围.
解:依题意,得AP=2t, BQ=4t.
∵AB=12, ∴PB=12-2t,
t的取值范围为0≤t≤6.
∴
∴
拓展延伸
解:由题意可得
解得m=1.
九马画山
在美丽的桂林有一处非常有名的景观叫“九马画山”,在一处石壁上的一些天然图案酷似各种形态的骏马。传说凡人只能找出两三匹马,谁要是找出其中的九匹马就能当“状元郎”。
在实践中感悟
横看成岭侧成峰,远近高低各不同
——变换角度分析问题
若函数y=x2m+n - 2xm-n+3是以x为自变量的二次函数,求m、n的值。
① ② ③ ④ ⑤
∵
2m+n=2
m-n=1
∴ m=1
n=0
∵
∴
2m+n=1
m-n=2
m=1
n=-1
∵
∴
2m+n=2
m-n=2
m=4/3
n=-2/3
∵
∴
2m+n=2
m-n=0
m=2/3
n=-4/3
∵
∴
2m+n=0
m-n=2
m=2/3
n=2/3
问题导入,列关系式
探索二次关系式共同点
总结二次函数概念
二次函数y=ax?+bx+c
(a,b,c为常数,a≠0)
二次函数的判别:
①含未知数的代数式为整式;
②未知数最高次数为2;
③二次项系数不为0.
确定二次函数解析式及自变量的取值范围
1.1 二次函数
1、什么叫函数?
在某变化过程中的两个变量x、y,当变量x在某个范围内取一个确定的值,另一个变量y总有唯一的值与它对应。
这样的两个变量之间的关系我们把它叫做函数关系。
对于上述变量x 、y,我们把y叫x的函数。 x叫自变量, y叫应变量。
目前,我们已经学习了那几种类型的函数?
知识回顾
二次函数
问题:如图,从喷头喷出的水珠,在空中走过一条曲线后落到池中央,在这条曲线的各个位置上,水珠的竖直高度h与它距离喷头的水平距离x之间有什么关系?
上面问题中变量之间的关系可以用哪一种函数来表示?这种函数与以前学习的函数、方程有哪些联系?
正方体的表面积y与棱长x的关系式为 ,y是x的函数吗?
知识点1
二次函数的概念
y=6x2
是
显然,对于x的每一个值,y都有一个对应值,即y是x的函数,它们的函数关系式为y=6x2 .
我们再来看几个问题。
问题1 n个球队参加比赛,每两队之间进行一场比赛。比赛的场次数m与球队数n有什么关系?
即,
m是n的函数吗?
某种产品现在的年产量为20t,计划今后两年增加产量。如果每年都比上一年的产量增加x倍,那么两年后这种产品的年产量y将随计划所定的x值而确定,y与x之间的关系应怎样表示?
问题2
产品原产量是20t,一年后的产量是原产量的 倍;再经过一年后的产量是一年后的产量的 倍.于是两年后的产量y与增加的倍数x的关系式为 .
(1+x)
(1+x)
y=20(1+x)2
y是x的函数吗?
y=20(1+x)2
y=20x2+40x+20
上述三个函数都是用自变量的二次式表示的。一般地,形如y=ax?+bx+c(a,b,c为常数,a≠0)
的函数,叫做二次函数。其中x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项。
二次项
一次项
常数项
二次函数的一般形式:
y=ax2+bx+c (其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时, y=ax2+c
当c=0时, y=ax2+bx
当b=0,c=0时, y=ax2
①y=6x2 ,
分别指出下列二次函数解析式的自变量、各项及各项系数。
出题角度一 二次函数的识别
下列函数中是二次函数的有 。
二次函数:y=ax?+bx+c
(a,b,c为常数,a≠0)
√
a=0
×
最高次数是4
×
×
√
①⑤
运用定义法判断一个函数是否为二次函数的步骤:
(1)将函数解析式右边整理为含自变量的代数式,左边是函数(因变量)的形式;
(2)判断右边含自变量的代数式是否是整式;
(3)判断自变量的最高次数是否是2;
(4)判断二次项系数是否不等于0.
出题角度二 应用二次函数的概念求相关字母的取值(或范围)
解:
根据二次函数的定义可得
解得m=3或m=-1.
当m=3时,y=6x2+9;当m=-1时,y=2x2-4x+1.
综上所述,该二次函数的解析式为:
y=6x2+9或y=2x2-4x+1.
练习
解:依题意,得
解得a=-1.
出题角度三 求二次函数的函数值
知识点2
根据具体问题确定二次函数解析式
①已知圆的面积y(cm2)与圆的半径x(cm),写出y与x之间的函数关系式;
②王先生存入银行2万元,先存一个一年定期,一年后银行将本息自动转存为又一个一年定期,设一年定期的存款年利率为x,两年后王先生共得本息和y万元,写出y与x之间的函数关系式;
③一个圆柱的高等于底面半径,写出它的表面积S与半径r之间的关系式.
y=πx2
y=2(1+x)2
S=4πr2
做一做:
(x>0)
(x>0)
(r>0)
说一说以上二次函数解析式的各项系数。
(2)设铺设地面所用瓷砖的总块数为y,请写出y与n的函数关系式
4.如图,用同样规格的正方形白色瓷砖铺设矩形地面,请观察下列图形并解答有关问题:
n=1
n=2
n=3
(1)在第n个图形中,每一横行共有 块瓷砖,每一竖列共有 块瓷砖(均用含n的代数式表示);
(n+3)
(n+2)
y=(n+3)(n+2)即 y=n?+5n+6
1. 下列函数是二次函数的是( )
A.y=2x+1 B.y=-2x+1 C.y=x2+2 D.y= x-2
2. 二次函数y=3x2-2x-4的二次项系数与常数项的和是( )
A.1 B.-1 C.7 D.-6
3.已知函数y=(a-1)x2+3x-1,若y是x的二次函数,则a的取值范围是 .
C
基础巩固
B
a≠1
4.某种商品的价格是2元,准备进行两次降价,如果每次降价的百分率都是x,则经过两次降价后的价格y(单位:元)与每次降价的百分率x的函数关系式是 .
5. 正方形的边长为10cm,在中间挖去一个边长为xcm的正方形,若剩余部分的面积为ycm2,则y与x的函数关系式是y=100-x2,x的取值范围为 .
6. 一辆汽车的行驶距离s(单位:m)与行驶时间t(单位:s)的函数关系式为s=9t+12t2,则经过12s汽车行驶了 m,行驶380m 需 s.
y=2(1-x)2
0≤x≤10
180
20
综合应用
7.如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,写出△PBQ的面积S与出发时间t(s)的函数关系式及t的取值范围.
解:依题意,得AP=2t, BQ=4t.
∵AB=12, ∴PB=12-2t,
t的取值范围为0≤t≤6.
∴
∴
拓展延伸
解:由题意可得
解得m=1.
九马画山
在美丽的桂林有一处非常有名的景观叫“九马画山”,在一处石壁上的一些天然图案酷似各种形态的骏马。传说凡人只能找出两三匹马,谁要是找出其中的九匹马就能当“状元郎”。
在实践中感悟
横看成岭侧成峰,远近高低各不同
——变换角度分析问题
若函数y=x2m+n - 2xm-n+3是以x为自变量的二次函数,求m、n的值。
① ② ③ ④ ⑤
∵
2m+n=2
m-n=1
∴ m=1
n=0
∵
∴
2m+n=1
m-n=2
m=1
n=-1
∵
∴
2m+n=2
m-n=2
m=4/3
n=-2/3
∵
∴
2m+n=2
m-n=0
m=2/3
n=-4/3
∵
∴
2m+n=0
m-n=2
m=2/3
n=2/3
问题导入,列关系式
探索二次关系式共同点
总结二次函数概念
二次函数y=ax?+bx+c
(a,b,c为常数,a≠0)
二次函数的判别:
①含未知数的代数式为整式;
②未知数最高次数为2;
③二次项系数不为0.
确定二次函数解析式及自变量的取值范围
同课章节目录
