浙教版八年级数学上册同步练习:2.8 直角三角形全等的判定(含答案)
文档属性
| 名称 | 浙教版八年级数学上册同步练习:2.8 直角三角形全等的判定(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 110.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-05 00:00:00 | ||
图片预览

文档简介
2.8 直角三角形全等的判定
课堂笔记
1. 直角三角形全等的判定:____________和一条____________对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“____________”).
2. 角平分线的性质:角的内部,到角的两边____________相等的点,在这个角的____________上.
分层训练
A组 基础训练
1. 如图,要用“HL”判定Rt△ABC和Rt△DEF全等的条件是( )
A. AC=DF,BC=EF B. ∠A=∠D,AB=DE
C. AC=DF,AB=DE D. ∠B=∠E,BC=EF
2. 根据下列条件,用尺规不能作出唯一直角三角形的是( )
A. 已知两直角边 B. 已知两锐角
C. 已知一直角边和一锐角 D. 已知斜边和一直角边
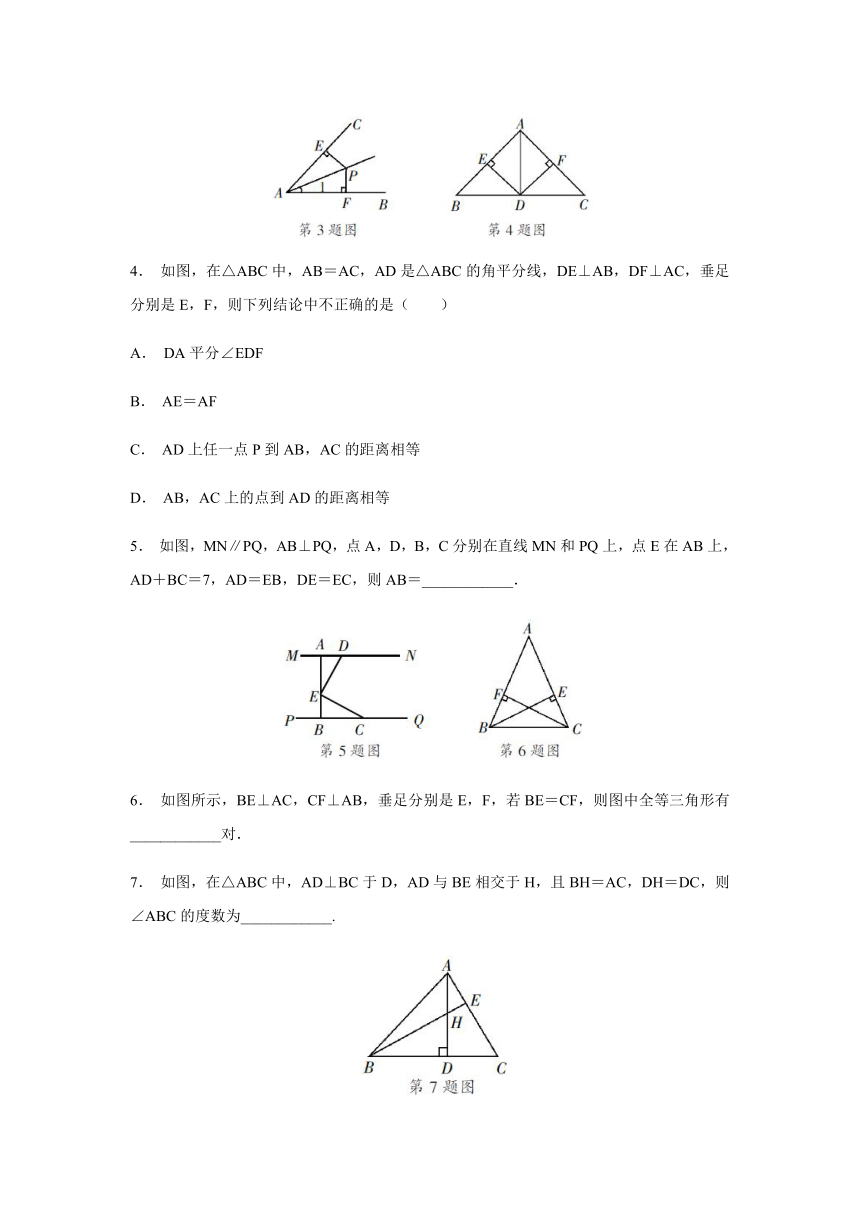
3. 如图,点P是∠CAB内一点,点P到AC,AB的距离分别为PE,PF,且PE=PF,若∠1=20°,则∠CAB等于( )
A. 20° B. 30° C. 40° D. 60°
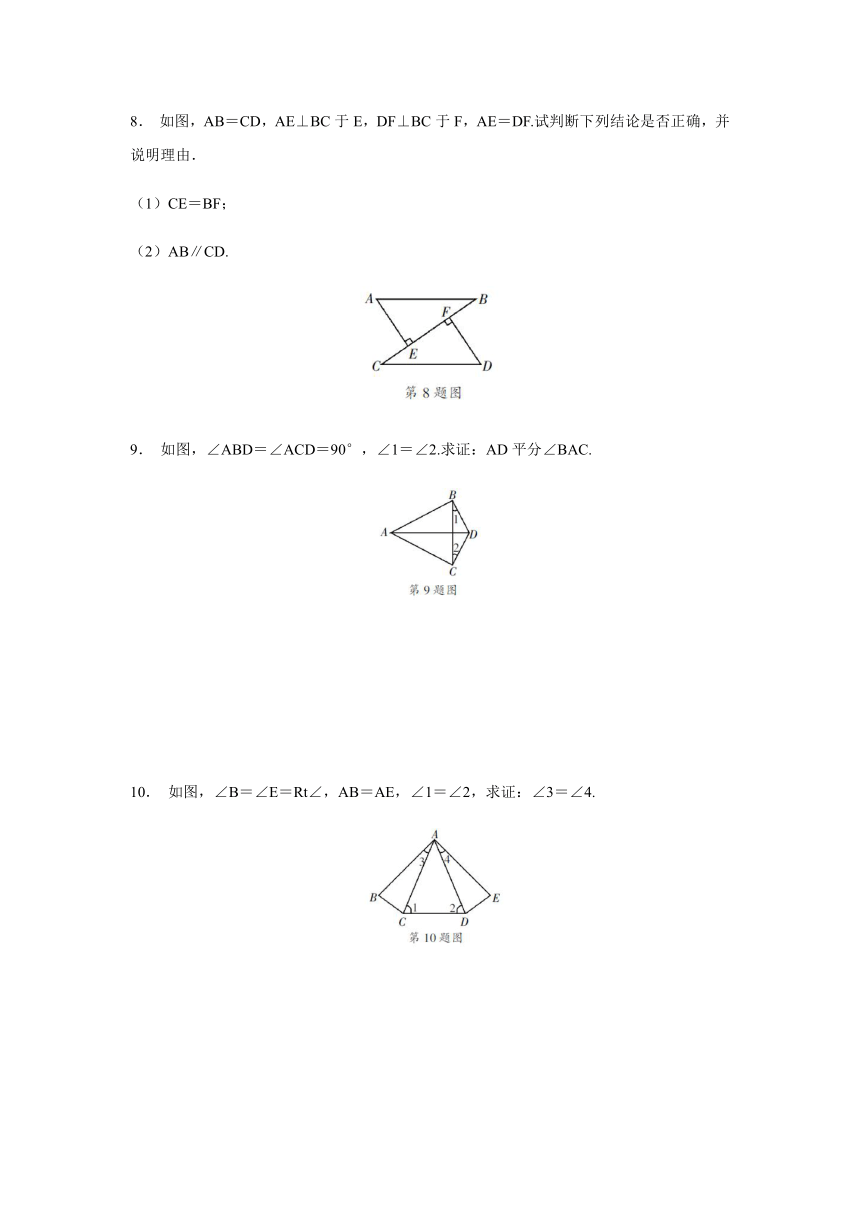
4. 如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,则下列结论中不正确的是( )
A. DA平分∠EDF
B. AE=AF
C. AD上任一点P到AB,AC的距离相等
D. AB,AC上的点到AD的距离相等
5. 如图,MN∥PQ,AB⊥PQ,点A,D,B,C分别在直线MN和PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=____________.
6. 如图所示,BE⊥AC,CF⊥AB,垂足分别是E,F,若BE=CF,则图中全等三角形有____________对.
7. 如图,在△ABC中,AD⊥BC于D,AD与BE相交于H,且BH=AC,DH=DC,则∠ABC的度数为____________.
8. 如图,AB=CD,AE⊥BC于E,DF⊥BC于F,AE=DF.试判断下列结论是否正确,并说明理由.
(1)CE=BF;
(2)AB∥CD.
9. 如图,∠ABD=∠ACD=90°,∠1=∠2.求证:AD平分∠BAC.
10. 如图,∠B=∠E=Rt∠,AB=AE,∠1=∠2,求证:∠3=∠4.
B组 自主提高
11.如图,∠BAC的平分线与BC的垂直平分线相交于D,过D作DE⊥AB于E,作DF⊥AC于F,若CD=5,DF=4,则BE=____________.
12. 如图,在直角三角形ABC中,∠C=90°,AC=20,BC=10,PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动,且点P不与点A,C重合,那么当点P运动到什么位置时,才能使△ABC与△APQ全等?
13. 如图,四边形ABCD中,AB=AD,AC平分∠BCD,AE⊥BC于点E,AF⊥CD于CD的延长线上的点F,BC=21,CD=9,求CF的长.
C组 综合运用
14. 如图1,点A,E,F,C在一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,且AB=CD.
(1)求证:BD平分EF;
(2)若将△DEC的边EC沿AC方向移动变为图2,其余的条件不变,上述结论是否仍成立?请说明理由.
参考答案
【课堂笔记】
1. 斜边 直角边 HL
2. 距离 平分线
【分层训练】
1—4. CBCD
5. 7
6. 3
7. 45°
8. (1)正确,用HL证明△ABE≌△DCF,可得CF=BE,则CE=BF;
(2)正确,由△ABE≌△DCF,可得∠B=∠C,则AB∥CD.
9. 由∠1=∠2,得BD=DC,再结合公共边AD,根据HL证明Rt△ABD≌Rt△ACD,则∠CAD=∠BAD,所以AD平分∠BAC.
10. 通过证Rt△ABC≌Rt△AED(HL)得∠3=∠4.
11. 3
12. 根据三角形全等的判定方法HL可知:
①当P运动到AP=BC时,∵∠C=∠QAP=90°,在Rt△ABC与Rt△QPA中,∴Rt△ABC
≌Rt△QPA(HL),即AP=BC=10;
②当P运动到与C点重合时,AP=AC,不合题意. 综上所述,当点P运动到距离点A为10时,△ABC与△APQ全等.
13. CF=15
14. (1)∵AE=CF,∴AE+EF=CF+EF,∴AF=CE. ∵BF⊥
AC,DE⊥AC,∴∠AFB=∠CED=90°. 又∵AB=CD,∴Rt△ABF≌Rt△CDE(HL),∴BF=DE. 又∵∠BGF=∠DGE,∴△BFG≌△DEG(AAS). ∴GF
=GE,即BD平分EF.
(2)结论仍成立. 理由如下:∵BF⊥AC,DE⊥AC,∴∠AFB=∠CED=90°. ∵AE=CF,∴AE-EF=CF-EF,即AF=CE. ∵AB=CD,∴Rt△ABF≌Rt△CDE
(HL). ∴BF=DE. 又∵∠BGF=∠DGE,∴△BFG
≌△DEG(AAS). ∴GF=GE,即BD平分EF.
课堂笔记
1. 直角三角形全等的判定:____________和一条____________对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“____________”).
2. 角平分线的性质:角的内部,到角的两边____________相等的点,在这个角的____________上.
分层训练
A组 基础训练
1. 如图,要用“HL”判定Rt△ABC和Rt△DEF全等的条件是( )
A. AC=DF,BC=EF B. ∠A=∠D,AB=DE
C. AC=DF,AB=DE D. ∠B=∠E,BC=EF
2. 根据下列条件,用尺规不能作出唯一直角三角形的是( )
A. 已知两直角边 B. 已知两锐角
C. 已知一直角边和一锐角 D. 已知斜边和一直角边
3. 如图,点P是∠CAB内一点,点P到AC,AB的距离分别为PE,PF,且PE=PF,若∠1=20°,则∠CAB等于( )
A. 20° B. 30° C. 40° D. 60°
4. 如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,则下列结论中不正确的是( )
A. DA平分∠EDF
B. AE=AF
C. AD上任一点P到AB,AC的距离相等
D. AB,AC上的点到AD的距离相等
5. 如图,MN∥PQ,AB⊥PQ,点A,D,B,C分别在直线MN和PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=____________.
6. 如图所示,BE⊥AC,CF⊥AB,垂足分别是E,F,若BE=CF,则图中全等三角形有____________对.
7. 如图,在△ABC中,AD⊥BC于D,AD与BE相交于H,且BH=AC,DH=DC,则∠ABC的度数为____________.
8. 如图,AB=CD,AE⊥BC于E,DF⊥BC于F,AE=DF.试判断下列结论是否正确,并说明理由.
(1)CE=BF;
(2)AB∥CD.
9. 如图,∠ABD=∠ACD=90°,∠1=∠2.求证:AD平分∠BAC.
10. 如图,∠B=∠E=Rt∠,AB=AE,∠1=∠2,求证:∠3=∠4.
B组 自主提高
11.如图,∠BAC的平分线与BC的垂直平分线相交于D,过D作DE⊥AB于E,作DF⊥AC于F,若CD=5,DF=4,则BE=____________.
12. 如图,在直角三角形ABC中,∠C=90°,AC=20,BC=10,PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动,且点P不与点A,C重合,那么当点P运动到什么位置时,才能使△ABC与△APQ全等?
13. 如图,四边形ABCD中,AB=AD,AC平分∠BCD,AE⊥BC于点E,AF⊥CD于CD的延长线上的点F,BC=21,CD=9,求CF的长.
C组 综合运用
14. 如图1,点A,E,F,C在一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,且AB=CD.
(1)求证:BD平分EF;
(2)若将△DEC的边EC沿AC方向移动变为图2,其余的条件不变,上述结论是否仍成立?请说明理由.
参考答案
【课堂笔记】
1. 斜边 直角边 HL
2. 距离 平分线
【分层训练】
1—4. CBCD
5. 7
6. 3
7. 45°
8. (1)正确,用HL证明△ABE≌△DCF,可得CF=BE,则CE=BF;
(2)正确,由△ABE≌△DCF,可得∠B=∠C,则AB∥CD.
9. 由∠1=∠2,得BD=DC,再结合公共边AD,根据HL证明Rt△ABD≌Rt△ACD,则∠CAD=∠BAD,所以AD平分∠BAC.
10. 通过证Rt△ABC≌Rt△AED(HL)得∠3=∠4.
11. 3
12. 根据三角形全等的判定方法HL可知:
①当P运动到AP=BC时,∵∠C=∠QAP=90°,在Rt△ABC与Rt△QPA中,∴Rt△ABC
≌Rt△QPA(HL),即AP=BC=10;
②当P运动到与C点重合时,AP=AC,不合题意. 综上所述,当点P运动到距离点A为10时,△ABC与△APQ全等.
13. CF=15
14. (1)∵AE=CF,∴AE+EF=CF+EF,∴AF=CE. ∵BF⊥
AC,DE⊥AC,∴∠AFB=∠CED=90°. 又∵AB=CD,∴Rt△ABF≌Rt△CDE(HL),∴BF=DE. 又∵∠BGF=∠DGE,∴△BFG≌△DEG(AAS). ∴GF
=GE,即BD平分EF.
(2)结论仍成立. 理由如下:∵BF⊥AC,DE⊥AC,∴∠AFB=∠CED=90°. ∵AE=CF,∴AE-EF=CF-EF,即AF=CE. ∵AB=CD,∴Rt△ABF≌Rt△CDE
(HL). ∴BF=DE. 又∵∠BGF=∠DGE,∴△BFG
≌△DEG(AAS). ∴GF=GE,即BD平分EF.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
