浙教版八年级数学上册同步练习:2.1 图形的轴对称(含答案)
文档属性
| 名称 | 浙教版八年级数学上册同步练习:2.1 图形的轴对称(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 172.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-05 00:00:00 | ||
图片预览

文档简介
第2章 特殊三角形
2.1 图形的轴对称
课堂笔记
1. 轴对称图形:如果把一个图形沿着一条直线折叠后,直线两侧的部分能够____________,那么这个图形叫做____________,这条直线叫做____________.
2. 性质:对称轴____________连结两个对称点的线段.
3. 轴对称:由一个图形变为另一个图形,并使这两个图形沿某一条直线折叠后能够____________,这样的图形改变叫做图形的轴对称,这条直线叫做____________.
4. 轴对称的性质:成轴对称的两个图形是全等图形.
分层训练
A组 基础训练
1. (盐城中考)下列图形中,是轴对称图形的是( )
2. 如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为( )
A. 55° B. 65°
C. 75° D. 85°
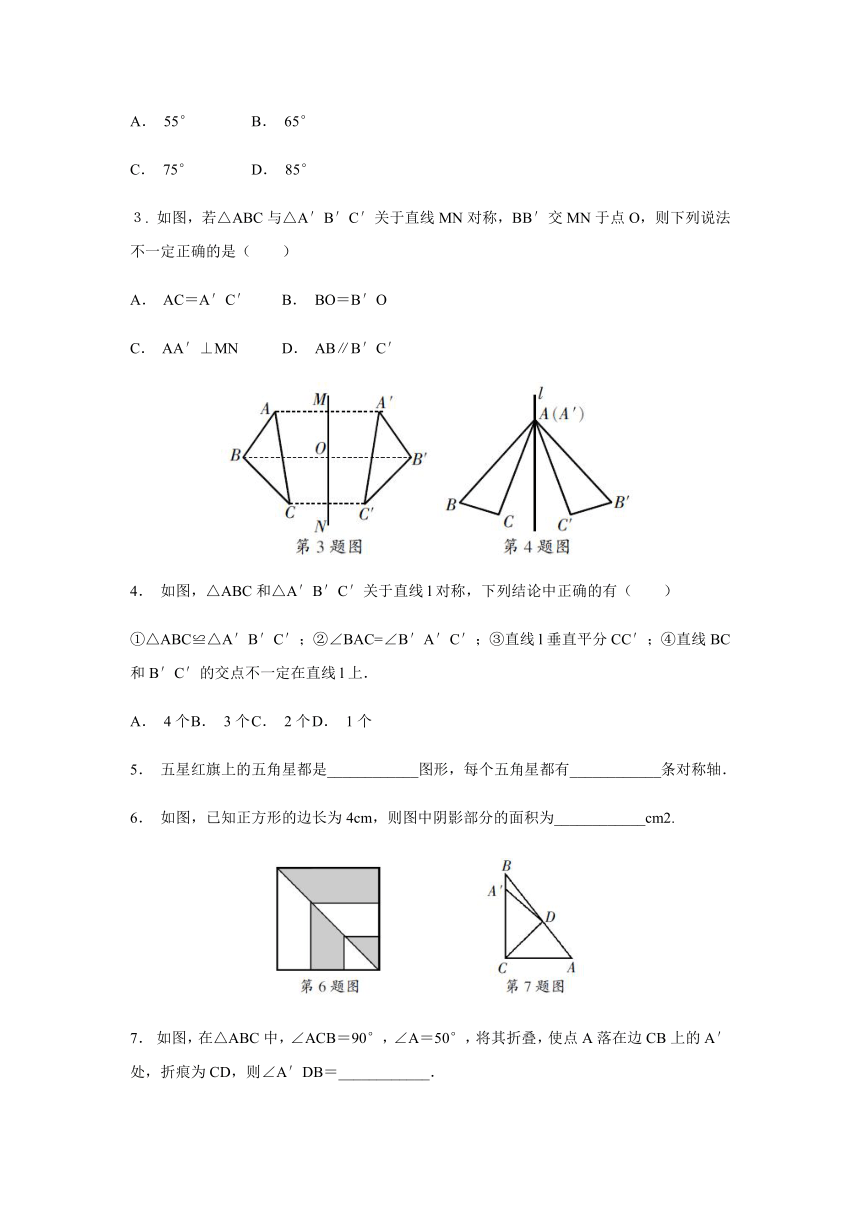
3. 如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )
A. AC=A′C′ B. BO=B′O
C. AA′⊥MN D. AB∥B′C′
4. 如图,△ABC和△A′B′C′关于直线l对称,下列结论中正确的有( )
①△ABC≌△A′B′C′;②∠BAC=∠B′A′C′;③直线l垂直平分CC′;④直线BC和B′C′的交点不一定在直线l上.
A. 4个 B. 3个 C. 2个 D. 1个
5. 五星红旗上的五角星都是____________图形,每个五角星都有____________条对称轴.
6. 如图,已知正方形的边长为4cm,则图中阴影部分的面积为____________cm2.
7. 如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上的A′处,折痕为CD,则∠A′DB=____________.
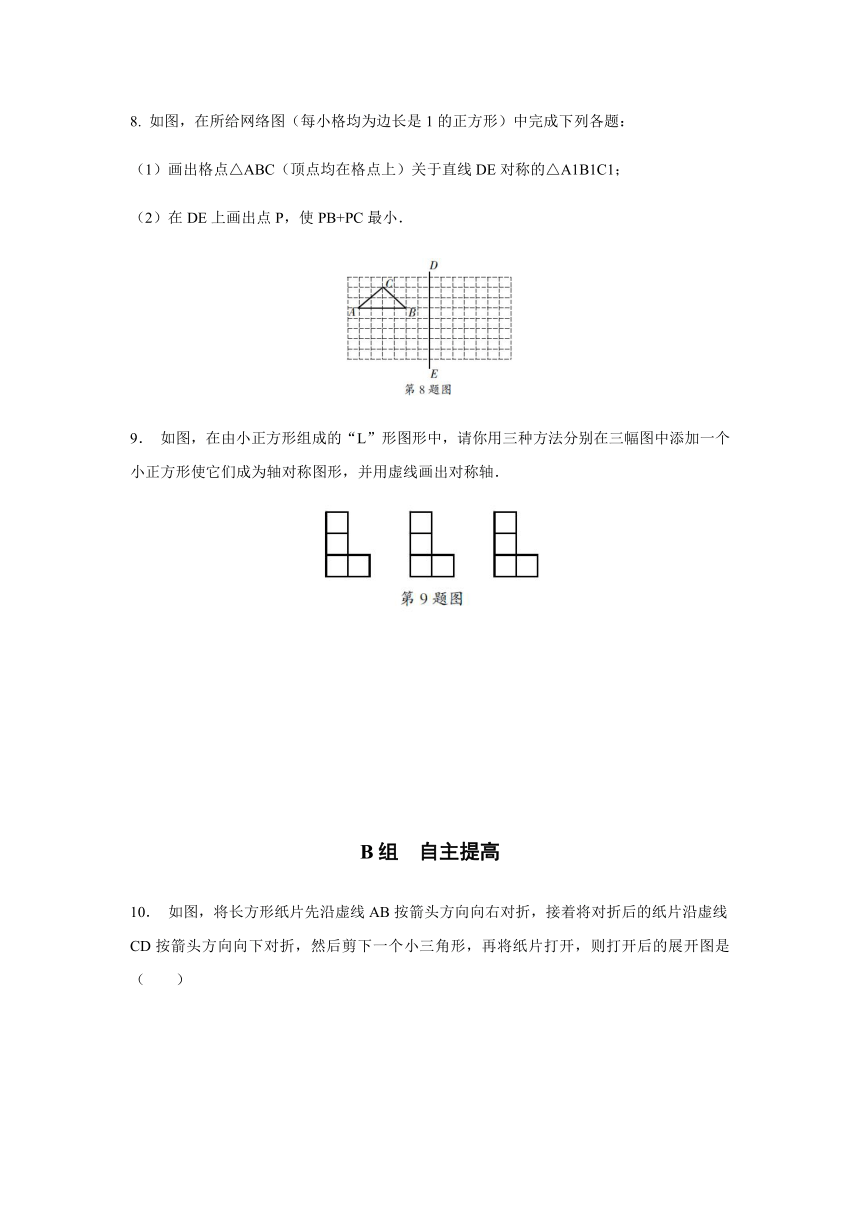
8. 如图,在所给网络图(每小格均为边长是1的正方形)中完成下列各题:
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点P,使PB+PC最小.
9. 如图,在由小正方形组成的“L”形图形中,请你用三种方法分别在三幅图中添加一个小正方形使它们成为轴对称图形,并用虚线画出对称轴.
B组 自主提高
10. 如图,将长方形纸片先沿虚线AB按箭头方向向右对折,接着将对折后的纸片沿虚线CD按箭头方向向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
11. 如图,已知正方形ABCD的边长为2,将正方形ABCD沿直线EF折叠,则图中折成的4个阴影三角形的周长之和为____________.
12. 如图均为2×2的正方形网格,每个小正方形的边长均为1. 请分别在四个图中各画出一个与△ABC成轴对称、顶点在格点上,且位置不同的三角形.
C组 综合运用
13. 如图,一牧马人从点A出发,到草地MN放牧,在傍晚回到帐篷B之前,先带马群到河边PQ去给马饮水. 试问:牧马人应走哪条线路才能使整个放牧的路程最短,写出作法.
参考答案
【课堂笔记】
1. 互相重合 轴对称图形 对称轴
2. 垂直平分
3. 互相重合 对称轴
【分层训练】
1—4. DBDB
5. 轴对称 5
6. 8
7. 10°
8. (1)如图,△A1B1C1即为所求;
(2)如图,点P即为所求.
9.
10. D
11. 8
12. 如图所示(答案不唯一)
13. 作法如下:
①作点A关于直线MN的对称点A′,点B关于直线PQ的对称点B′;
②连结A′B′交MN于点C,交PQ于点D;
③连结AC,BD,则牧马人应走的线路为A→C→D→B.
2.1 图形的轴对称
课堂笔记
1. 轴对称图形:如果把一个图形沿着一条直线折叠后,直线两侧的部分能够____________,那么这个图形叫做____________,这条直线叫做____________.
2. 性质:对称轴____________连结两个对称点的线段.
3. 轴对称:由一个图形变为另一个图形,并使这两个图形沿某一条直线折叠后能够____________,这样的图形改变叫做图形的轴对称,这条直线叫做____________.
4. 轴对称的性质:成轴对称的两个图形是全等图形.
分层训练
A组 基础训练
1. (盐城中考)下列图形中,是轴对称图形的是( )
2. 如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为( )
A. 55° B. 65°
C. 75° D. 85°
3. 如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )
A. AC=A′C′ B. BO=B′O
C. AA′⊥MN D. AB∥B′C′
4. 如图,△ABC和△A′B′C′关于直线l对称,下列结论中正确的有( )
①△ABC≌△A′B′C′;②∠BAC=∠B′A′C′;③直线l垂直平分CC′;④直线BC和B′C′的交点不一定在直线l上.
A. 4个 B. 3个 C. 2个 D. 1个
5. 五星红旗上的五角星都是____________图形,每个五角星都有____________条对称轴.
6. 如图,已知正方形的边长为4cm,则图中阴影部分的面积为____________cm2.
7. 如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上的A′处,折痕为CD,则∠A′DB=____________.
8. 如图,在所给网络图(每小格均为边长是1的正方形)中完成下列各题:
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点P,使PB+PC最小.
9. 如图,在由小正方形组成的“L”形图形中,请你用三种方法分别在三幅图中添加一个小正方形使它们成为轴对称图形,并用虚线画出对称轴.
B组 自主提高
10. 如图,将长方形纸片先沿虚线AB按箭头方向向右对折,接着将对折后的纸片沿虚线CD按箭头方向向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
11. 如图,已知正方形ABCD的边长为2,将正方形ABCD沿直线EF折叠,则图中折成的4个阴影三角形的周长之和为____________.
12. 如图均为2×2的正方形网格,每个小正方形的边长均为1. 请分别在四个图中各画出一个与△ABC成轴对称、顶点在格点上,且位置不同的三角形.
C组 综合运用
13. 如图,一牧马人从点A出发,到草地MN放牧,在傍晚回到帐篷B之前,先带马群到河边PQ去给马饮水. 试问:牧马人应走哪条线路才能使整个放牧的路程最短,写出作法.
参考答案
【课堂笔记】
1. 互相重合 轴对称图形 对称轴
2. 垂直平分
3. 互相重合 对称轴
【分层训练】
1—4. DBDB
5. 轴对称 5
6. 8
7. 10°
8. (1)如图,△A1B1C1即为所求;
(2)如图,点P即为所求.
9.
10. D
11. 8
12. 如图所示(答案不唯一)
13. 作法如下:
①作点A关于直线MN的对称点A′,点B关于直线PQ的对称点B′;
②连结A′B′交MN于点C,交PQ于点D;
③连结AC,BD,则牧马人应走的线路为A→C→D→B.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
