浙教版七上数学1.3绝对值课件(15张PPT)
文档属性
| 名称 | 浙教版七上数学1.3绝对值课件(15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-07 16:15:52 | ||
图片预览





文档简介
(共15张PPT)
0
1
2
3
4
-1
-2
-3
1,在数轴上找到表示+3 ,-3的点,
2,+3,-3是互为相反数吗?为什么是?
说法一:
说法二:
如何用数学语言来描述表示+3,-3的点到原点的
距离相等:
A
B
5
5
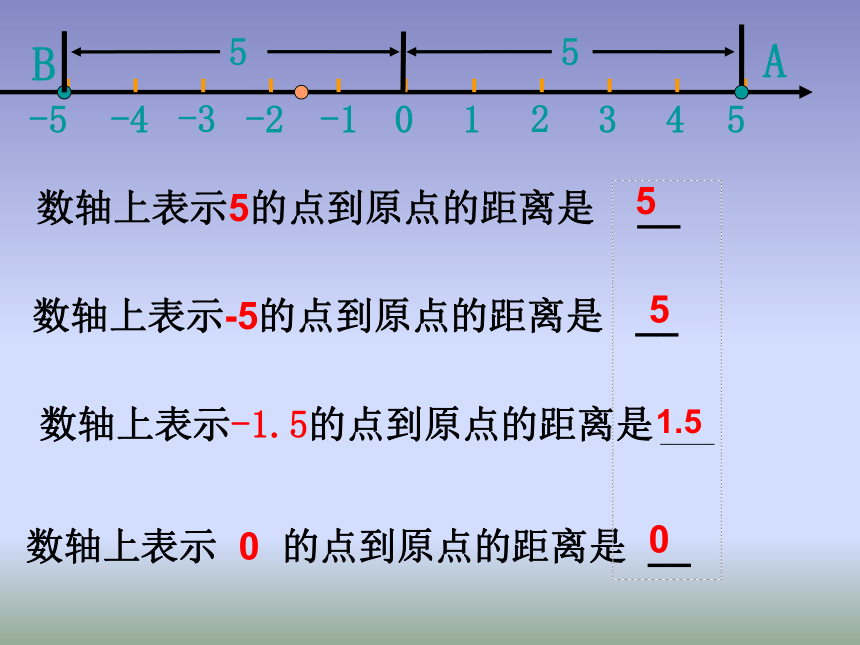
数轴上表示5的点到原点的距离是 __
数轴上表示-5的点到原点的距离是 __
数轴上表示-1.5的点到原点的距离是
数轴上表示 0 的点到原点的距离是 __
5
5
0
1.5
如,+5到原点的距离是5, ∴ +5的绝对值是5,记作|+5| = 5;
在数轴上,一个数所对应的点到原点的距离叫做该数的绝对值 (几何定义)
-5的绝对值是5,记作|- 5| = 5.
注意:①与原点的关系 ②是一个距离
2.表示2.8的点与原点的距离是 , 即2.8的绝对值是 ,记作 ;
1.表示+7的点与原点的距离是 ,即+7的绝值是 ,记作 ;
练习:
3.表示0的点与原点的距离是 ,即0的绝对值是 ,记作 ;
4. 表示-5的点与原点的距离是 ,即-5的绝对值是 ,记作 ;
7
7
2.8
2.8
0
0
5
5
求下列各数的绝对值:
解:
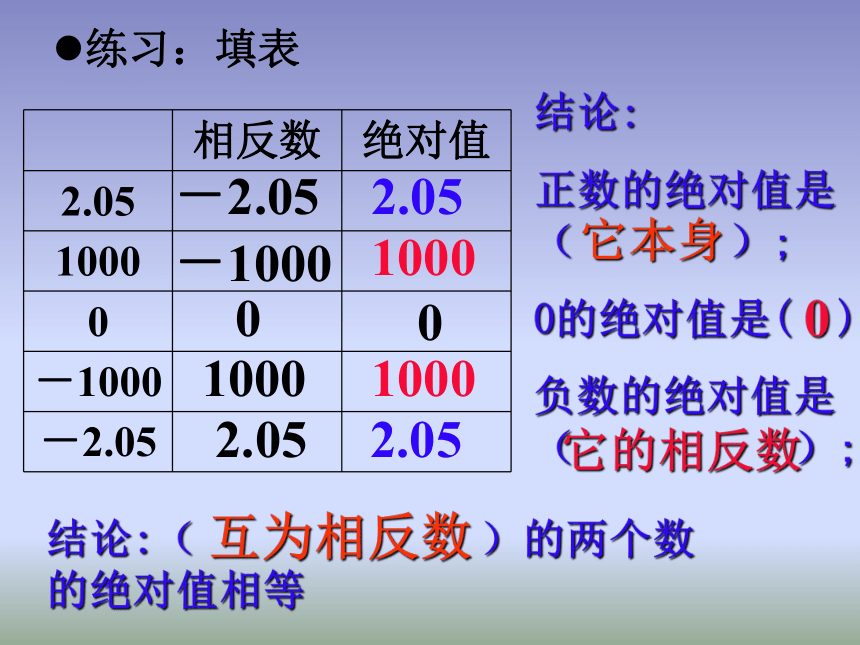
练习:填表
结论:
正数的绝对值是 ( );
0的绝对值是( )
负数的绝对值是( );
结论:( )的两个数 的绝对值相等
它本身
0
它的相反数
互为相反数
相反数 绝对值
2.05
1000
0
-1000
-2.05
判断题
(1)有理数的绝对值一定是正数( )
(2)如果两个数的绝对值相等,那么这两个数相等( )
(3)如果一个数是正数,那么这个数的绝对值是它本身( )
(4)如果一个数的绝对值是它本身, 那么这个数是正数( )
例2
求绝对值等于4的数。
解:
∵数轴上到原点的距离等于4个单位长度的点有两个,即表示+4的点P和-4的点M,
∴绝对值等于4的数是+4和-4.
口答:绝对值是5、1.6、0的数。
解: ∵ |+4|=4 |-4|=4
∴绝对值等于4的数是+4和-4.
求绝对值等于4的数。
例2
计算:
解:
|-9| + |+1|
|-10| — |-8|
原式=9+1
=10
1.绝对值的几何定义
2.绝对值的性质:(代数定义)
(1)正数的绝对值是它本身;
(2)负数的绝对值是它的相反数:
(3)0的绝对值是0
(4)互为相反数的两个数的绝对值相等.
小结:
数轴上到-1的距离等于3的数是多少?
解:
∵数轴上到-1的距离等于3个单位长度的点有两个,即表示+2的点P和-4的点M,
∴数轴上到-1的距离等于3的数是2和-4
检查了5个排球的重量(单位:克),其中超过标
标准重量的数量记为正数,不足的数量记为负数,
结果如下:
其中哪个球的重量最接近标准?怎样用绝对值
解释排球的重量接近标准重量的程度?
练一练
+
(2)绝对值小于 10 的整数有( )个。
(3)绝对值不大于 7 的负整数是( )。
(1)绝对值等于4的数是( )
+4, -4
19
-1,-2,-3,-4,-5,-6,-7
+1,-1,+2,-2
0
1
2
3
4
-1
-2
-3
1,在数轴上找到表示+3 ,-3的点,
2,+3,-3是互为相反数吗?为什么是?
说法一:
说法二:
如何用数学语言来描述表示+3,-3的点到原点的
距离相等:
A
B
5
5
数轴上表示5的点到原点的距离是 __
数轴上表示-5的点到原点的距离是 __
数轴上表示-1.5的点到原点的距离是
数轴上表示 0 的点到原点的距离是 __
5
5
0
1.5
如,+5到原点的距离是5, ∴ +5的绝对值是5,记作|+5| = 5;
在数轴上,一个数所对应的点到原点的距离叫做该数的绝对值 (几何定义)
-5的绝对值是5,记作|- 5| = 5.
注意:①与原点的关系 ②是一个距离
2.表示2.8的点与原点的距离是 , 即2.8的绝对值是 ,记作 ;
1.表示+7的点与原点的距离是 ,即+7的绝值是 ,记作 ;
练习:
3.表示0的点与原点的距离是 ,即0的绝对值是 ,记作 ;
4. 表示-5的点与原点的距离是 ,即-5的绝对值是 ,记作 ;
7
7
2.8
2.8
0
0
5
5
求下列各数的绝对值:
解:
练习:填表
结论:
正数的绝对值是 ( );
0的绝对值是( )
负数的绝对值是( );
结论:( )的两个数 的绝对值相等
它本身
0
它的相反数
互为相反数
相反数 绝对值
2.05
1000
0
-1000
-2.05
判断题
(1)有理数的绝对值一定是正数( )
(2)如果两个数的绝对值相等,那么这两个数相等( )
(3)如果一个数是正数,那么这个数的绝对值是它本身( )
(4)如果一个数的绝对值是它本身, 那么这个数是正数( )
例2
求绝对值等于4的数。
解:
∵数轴上到原点的距离等于4个单位长度的点有两个,即表示+4的点P和-4的点M,
∴绝对值等于4的数是+4和-4.
口答:绝对值是5、1.6、0的数。
解: ∵ |+4|=4 |-4|=4
∴绝对值等于4的数是+4和-4.
求绝对值等于4的数。
例2
计算:
解:
|-9| + |+1|
|-10| — |-8|
原式=9+1
=10
1.绝对值的几何定义
2.绝对值的性质:(代数定义)
(1)正数的绝对值是它本身;
(2)负数的绝对值是它的相反数:
(3)0的绝对值是0
(4)互为相反数的两个数的绝对值相等.
小结:
数轴上到-1的距离等于3的数是多少?
解:
∵数轴上到-1的距离等于3个单位长度的点有两个,即表示+2的点P和-4的点M,
∴数轴上到-1的距离等于3的数是2和-4
检查了5个排球的重量(单位:克),其中超过标
标准重量的数量记为正数,不足的数量记为负数,
结果如下:
其中哪个球的重量最接近标准?怎样用绝对值
解释排球的重量接近标准重量的程度?
练一练
+
(2)绝对值小于 10 的整数有( )个。
(3)绝对值不大于 7 的负整数是( )。
(1)绝对值等于4的数是( )
+4, -4
19
-1,-2,-3,-4,-5,-6,-7
+1,-1,+2,-2
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
