2.1-2.4 等腰三角形的判定定理同步测试题(含答案)
文档属性
| 名称 | 2.1-2.4 等腰三角形的判定定理同步测试题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-23 06:53:12 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
初中数学JBY单元检测卷
2.1~2.4等腰三角形
一、选择题(每小题3分,共30分)
1.若等腰三角形的顶角为80°,则它的一个底角度数为( )
A.?20°?????????? ??B.?50°? ??????????????????????C.?80°???????????? D.?100°
2.小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,
则电子表的实际时刻是( )
A.15:01?? B.10:51???C.10:21?? D.12:01
3.已知一个等腰三角形有两内角的度数之比为1:4,则这个等腰三角形顶角的度数为(?? )
A.?20?°????????????????????????????????B.?120°?????????????????????????????????C.?20°或 120°?????????????????????????????????D.?36°
4.如图,△ABC中,AB=AC,AD⊥BC,下列结论中不一定正确的是(?? )
A.?D是BC中点???????????????????????B.?AD平分∠BAC???????????????????????C.?AB=2BD???????????????????????D.?∠B=∠C
5.下列有关等腰三角形的说法中,正确的是(?? )
A.?腰对应相等的两个等腰三角形全等??????????????????????????????????????B.?等腰三角的高线与中线相互重合
C.?等腰三角形两腰上的中线相等???????????????????????????? D.?等腰三角的最大角必大于60°?
6.如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( )
A.1号袋? ????????????????????????? B.2号袋 C.3号袋? ????????????????????????? D.4号袋
7.如图,在△ABC中,∠CAB=130°,AB、AC的垂直平分线分别交BC于点E、F则∠EAF等于(???)
A.60°???????B.70°?????? C.80°????????? D.90°
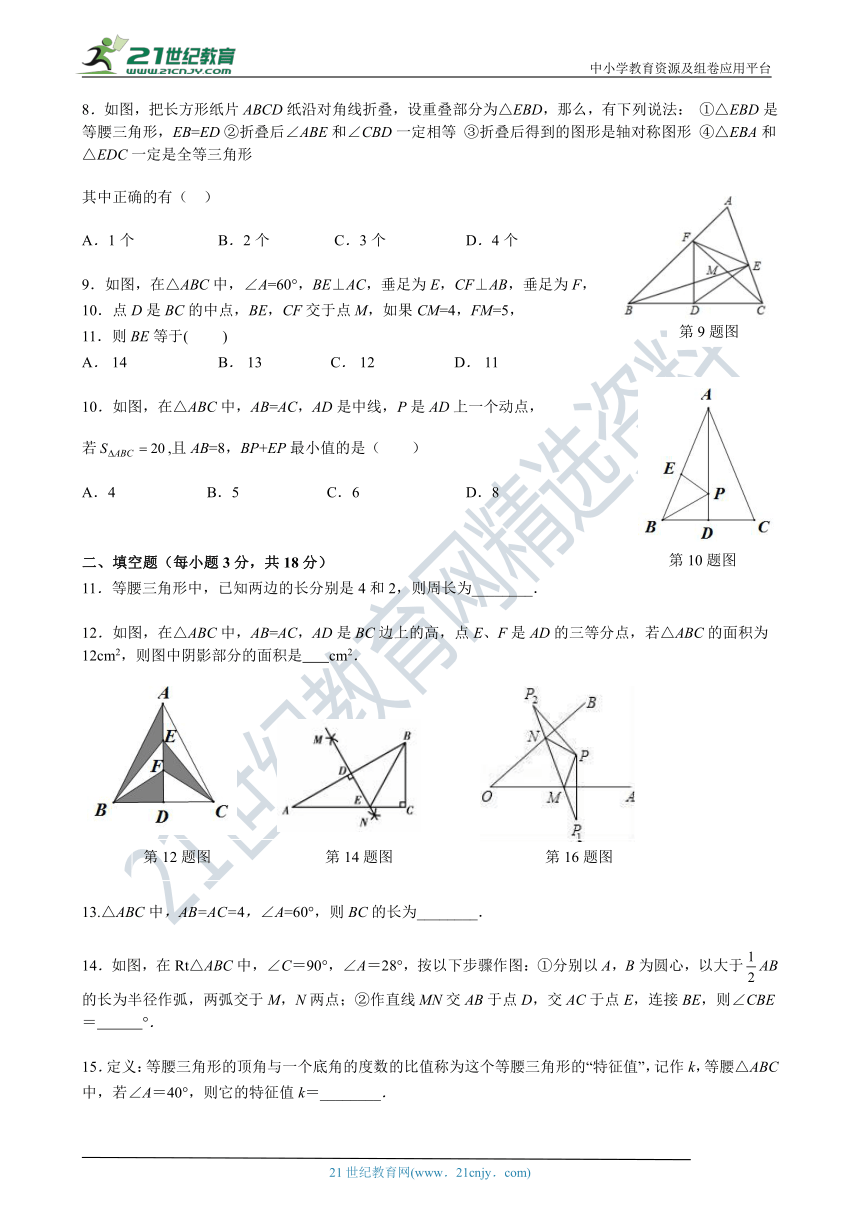
8.如图,把长方形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么,有下列说法: ①△EBD是等腰三角形,EB=ED?②折叠后∠ABE和∠CBD一定相等??③折叠后得到的图形是轴对称图形 ④△EBA和△EDC一定是全等三角形
其中正确的有(????)
A.1个???? B.2个? C.3个??? D.4个
如图,在△ABC中,∠A=60°,BE⊥ (?http:?/??/?www.21cnjy.com?)AC,垂足为E,CF⊥AB,垂足为F,
点D是BC的中点,BE,CF交于点M,如果CM=4,FM=5,
则BE等于(? )
A.?14????????????????????????B.?13??????????????????C.?12?????????????????????D.?11
10.如图,在△ABC中,AB=AC,AD是中线,P是AD上一个动点,
若,且AB=8,BP+EP最小值的是( )
A.4 B.5 ? C.6 D.8
二、填空题(每小题3分,共18分)
11.等腰三角形中,已知两边的长分别是4和2,则周长为________.
12.如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD的三等分点,若△ABC的面积为12cm2,则图中阴影部分的面积是???????cm2.
13.△ABC中,AB=AC=4,∠A=60°,则BC的长为________.
14.如图,在Rt△ABC中,∠C=90°,∠A=28°,按以下步骤作图:①分别以A,B为圆心,以大于AB的长为半径作弧,两弧交于M,N两点;②作直线MN交AB于点D,交AC于点E,连接BE,则∠CBE=??? ?°.
15.定义:等腰三角形的顶角与一个底角的度数的比值称为这个等腰三角形的“特征值”,记作k,等腰△ABC中,若∠A=40°,则它的特征值k=________.
16.如图所示,∠AOB=40°,点P为∠AOB内的一点,分别作出P点关于OA,OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为 ?? ,∠MPN= ?? °.
三、解答题(共52分)
17.(6分)如图,已知△ABC.
(1)作边BC的垂直平分线MN;
(2)作∠C的平分线CD交MN于点D.(要求:不写作法,保留作图痕迹)
(6分)如图,四边形 ABCD中, AB=AC,∠B=∠C .
求证: BD=CD.
19.(6分)如图,△ABC是等腰三角形,∠B=∠C,AD是底边BC上的高,DE∥AB交AC于点E.试说明△ADE是等腰三角形.
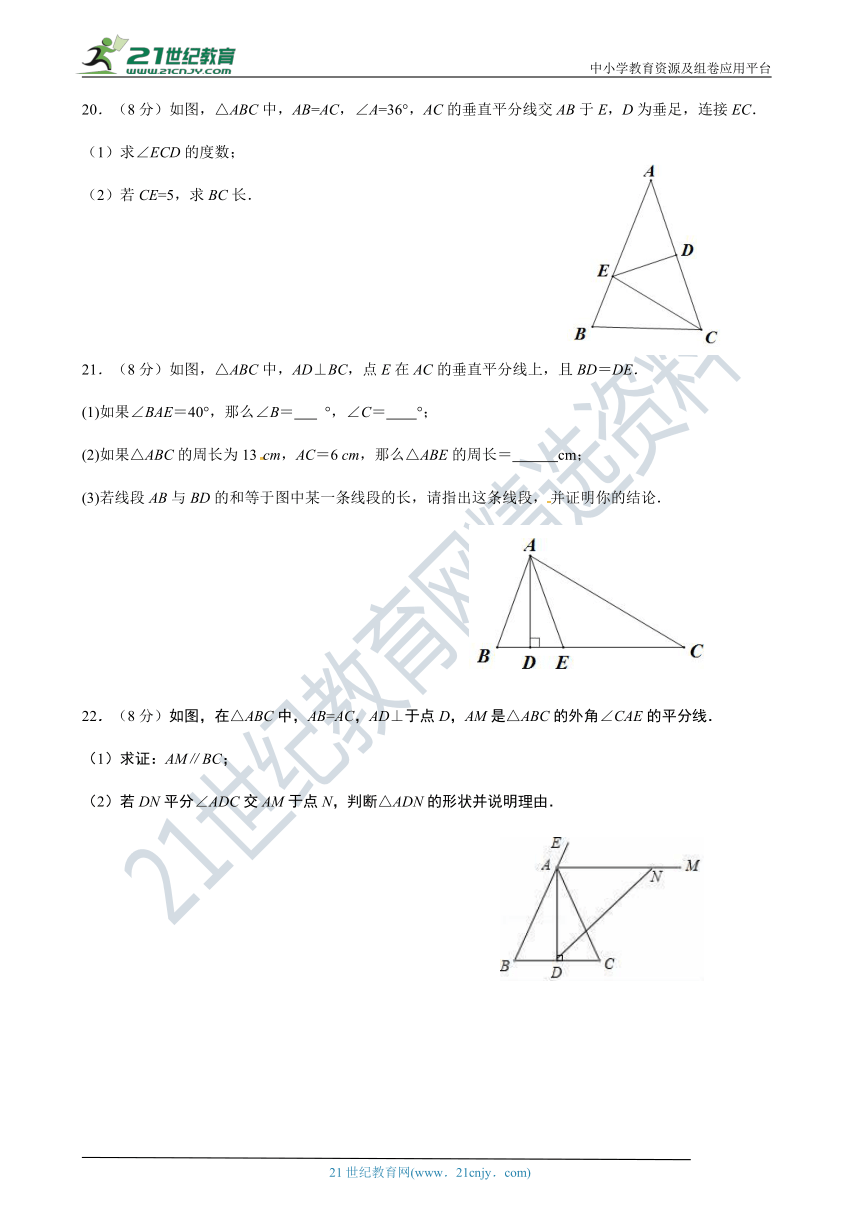
20.(8分)如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
21.(8分)如图,△ABC中,AD⊥BC,点E在AC的垂直平分线上,且BD=DE.
(1)如果∠BAE=40°,那么∠B= °,∠C= °;
(2)如果△ABC的周长为13?cm,AC=6?cm,那么△ABE的周长= cm;
(3)若线段AB与BD的和等于图中某一条线段的长,请指出这条线段,并证明你的结论.
22.(8分)如图,在△ABC中,AB=AC,AD⊥于点D,AM是△ABC的外角∠CAE的平分线.
(1)求证:AM∥BC;
(2)若DN平分∠ADC交AM于点N,判断△ADN的形状并说明理由.
23.(10分)在等边△ABC外侧作直线AP,点B关于直线AP的对称点为D,连接BD,CD,其中CD交直线AP于点E.?
(1)依题意补全图1;???
(2)若∠PAB=30°,求∠ACE的度数;???
(3)如图2,若60°<∠PAB<120°,判断由线段AB,CE,ED可以构成一个含有多少度角的三角形,并证明.?
附加题:24.如图,在Rt△ABC中,∠B=9 (?http:?/??/?www.21cnjy.com?)0°,AC=10,∠C=30°点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.
(1)DF=________;(用含t的代数式表示)
(2)求证:△AED≌△FDE;
(3)当t为何值时,△DEF是等边三角形?说明理由;
(4)当t为何值时,△DEF为直角三角形?(请直接写出t的值.)
答案:
选择题:
BBCCC BCCCB
填空题:
11.10
12.6
13.4
14.34
或
15,100
三、解答题?
略
18.连接BC,∵AB=AC,∴∠ABC=∠ACB,∵∠ABD=∠ACD,∴∠DBC=∠DCB∴BD=CD
19.∵在△ABC中,∠B=∠C,
∴AB=AC,
∵AD⊥BC,
∴∠BAD=∠DAC,
∵DE∥AB,
∴∠ADE=∠BAD,
∴∠ADE=∠DAC,
∴AE=ED,
∴△ADE是等腰三角形.
20.(1)∵DE垂直平分AC,
∴CE=AE,∴∠ECD=∠A=36°;
(2)∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∴∠BEC=∠A+∠ECD=72°,
∴∠BEC=∠B,
∴BC=EC=5.
21.(1)70,35;(2)7;(3)AB+BD=DC.证明:∵AD⊥BC,BD=DE,∴AB=AE,∵点E在AC的垂直平分线上,∴AE=CE,∴AB+BD=AE+DE=CE+DE=DC.
22.(1)∵AB=AC,AD⊥BC,∴∠BAD=∠CAD=.
∵AM平分∠EAC,∴∠EAM=∠MAC=.∴∠MAD=∠MAC+∠DAC=90°.
∵AD⊥BC∴∠ADC=90°∴∠MAD+∠ADC=180°∴AM∥BC.
(2)△ADN是等腰直角三角形,理由是:∵AM∥AD,∴∠AND=∠NDC,∵DN平分∠ADC,
∴∠ADN=∠NDC=∠AND.∴AD=AN,∴△ADN是等腰直角三角形.
23.(1)解:所作图形如图1所示:?
INCLUDEPICTURE \d "http://czsx.cooco.net.cn/files/down/test/2019/06/16/05/2019061605052341658020.files/image041.jpg" \* MERGEFORMATINET
(2)解:连接AD,如图1.?∵点D与点B关于直线AP对称,∴AD=AB,∠DAP=∠BAP=30°,∵AB=AC,∠BAC=60°,∴AD=AC,∠DAC=120°,∴2∠ACE+60°+60°=180°,∴∠ACE=30°
(3)解:线段AB,CE,ED可以构成一个含有60°角的三角形.?
证明:连接AD,EB,如图2.
∵点D与点B关于直线AP对称,∴AD=AB,DE=BE,∴∠EDA=∠EBA,∵AB=AC,AB=AD,
∴AD=AC,∴∠ADE=∠ACE,∴∠ABE=∠ACE.设AC,BE交于点F,
又∵∠AFB=∠CFE,∴∠BAC=∠BEC=60°,∴线段AB,CE,ED可以构成一个含有60°角的三角形.
24.(1)t(2)证明:∵∠CFD=90°,∠B=90°, ∴DF∥AB,
∴∠AED=∠FDE.在△AED和△FDE中,AF=FD=t,∠AED=∠FDE,DE=DE,∴△AED≌△FDE(SAS).
(3)∵△AED≌△FDE, ∴当△DEF是等边三角形时,△EDA是等边三角形.∵∠A=90°﹣∠C=60°,
∴AD=AE.∵AE=t,AD=AC﹣CD=10﹣2t,∴t=10﹣2t,
∴t= ,
∴当t为时,△DEF是等边三角形.
(4)∵△AED≌△FDE,
∴当△DEF为直角三角形时,△EDA是直角三角形.
当∠AED=90°时,AD=2AE,即10﹣2t=2t,
解得:t=;当∠ADE=90°时,AE=2AD,即t=2(10﹣2t),解得:t=4.
综上所述:当t为 或4时,△DEF为直角三角形.
(?http:?/??/?www.21cnjy.com?/??)
-
17com
第2题图
第4题图 第6题图 第7题图 第8题图
第9题图
第10题图
第12题图 第14题图 第16题图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
