2.7探索勾股定理(2)课件(16张ppt)
文档属性
| 名称 | 2.7探索勾股定理(2)课件(16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-21 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
--------直角三角形的判定
(1)有一个角是直角 的三角形是直角三角形;
(2)有两个角的和是90°的三角形是直角三角形;
角
一个三角形满足什么条件时,能判定它是直角三角形?
大约在公元前2700年,古埃及人已经建成了世界闻名的七十多座大大小小的金字塔。当时的生产工具很落后,没有直角三角板,更没有任何的先进的测量仪器。可是,这些金字塔的塔基却都是正方形,这确实是个谜?古埃及人是用什么方法得到直角呢?
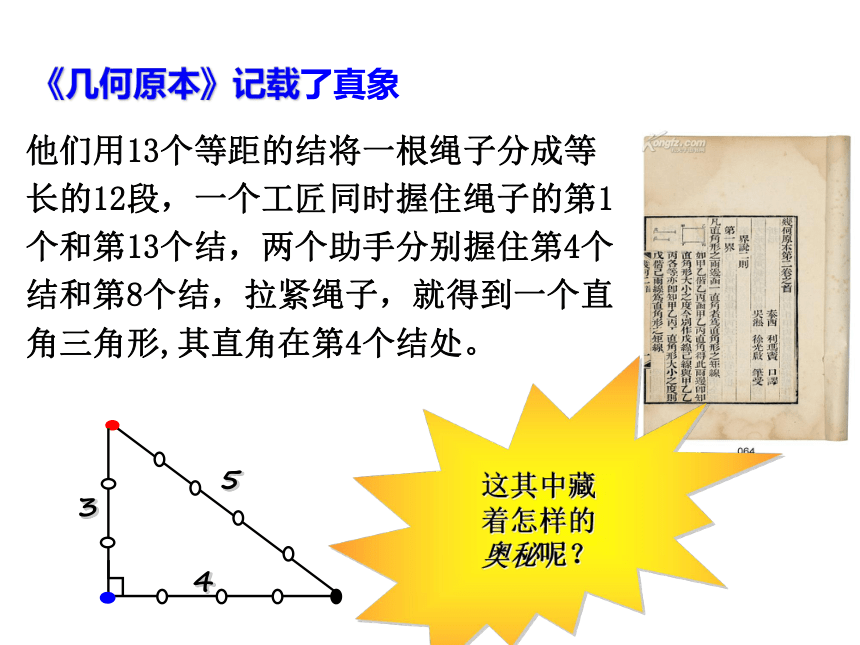
《几何原本》记载了真象
他们用13个等距的结将一根绳子分成等长的12段,一个工匠同时握住绳子的第1个和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就得到一个直角三角形,其直角在第4个结处。
这其中藏
着怎样的
奥秘呢?
3
4
5
1.画一画:画出边长分别是下列各组数的三角形(单位:厘米) :
①6, 8, 10; ② 2.5 , 6, 6.5.
2.测一测:用量角器分别测量一下上述各三角形的最大度数:
1:_______ 2:_______
3.判断:请判断一下上述你所画的三角形的形状.
A:______ B:_______
直角三角形
直角三角形
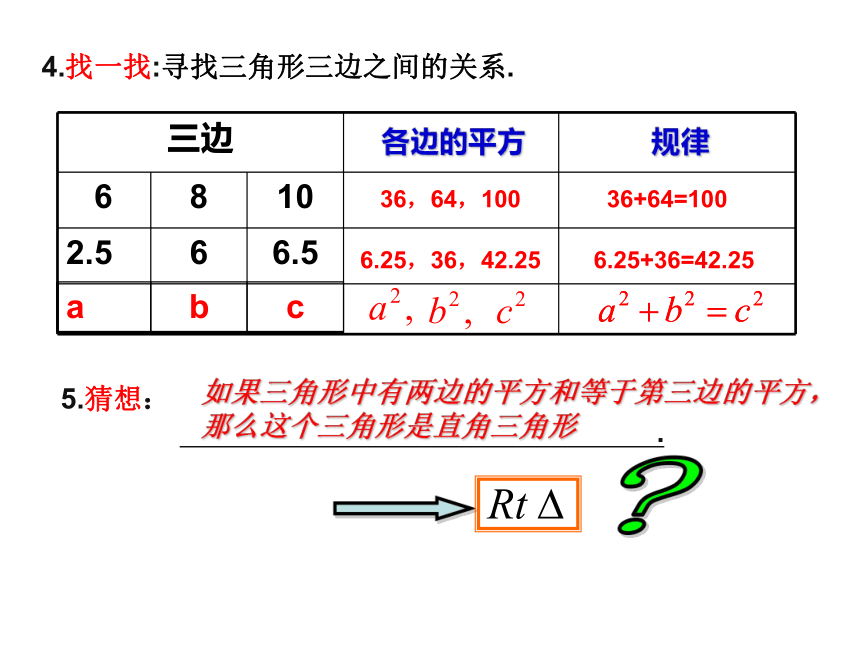
5.猜想:
4.找一找:寻找三角形三边之间的关系.
如果三角形中有两边的平方和等于第三边的平方,那么这个三角形是直角三角形
36,64,100
36+64=100
各边的平方
规律
6.25,36,42.25
6.25+36=42.25
.
三边
6 8 10
2.5 6 6.5
a b c
a
c
b
A
C
B
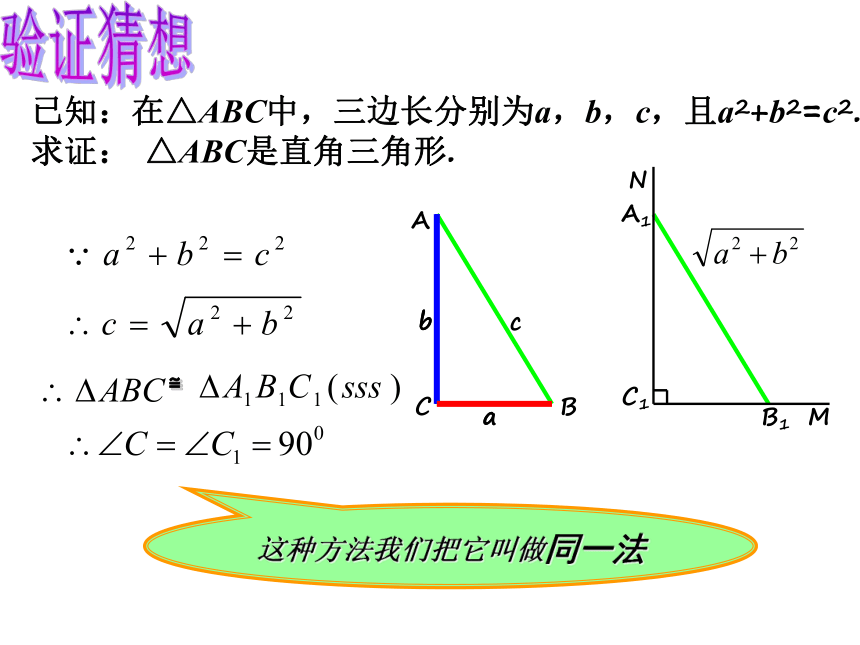
已知:在△ABC中,三边长分别为a,b,c,且a2+b2=c2.
求证: △ABC是直角三角形.
这种方法我们把它叫做同一法
如果三角形中 有两边的平方和 等于第三边的平方,那么这个三角形是直角三角形.
数
形
最长边所对的角是直角
那直角的位
置该如何确
定呢?
较短两边的平方和
最长边的平方
根据下列条件,分别判断以a,b,c为边的△ABC是不是直角三角形,如果是,指出哪条边所对的角是直角.
(1)a=7,b=24,c=25;
(2) a:b:c=
1、先求各边的平方
2、观察较短两边的平方和与最长边的平方
3、判断是否相等
下面以a,b,c为边长且所对角分别为∠A ∠B ,∠C的三角形是不是直角三角形?如果是那么哪一个角是直角?
(2)a=7n, b=25n, c=24n (n为正整数);
(1) a= b= 2 c= ;
____ _______;
是
∠ A=90°
是
∠ B=90°
是
∠ C=90°
a=m2-n2,b=2mn,c=m2+n2 (m>n,m,n是正整数)
2.小蒋要求△ABC的的最长边上的高,测得AB=8cm,
AC=6cm,BC=10cm。则可知最长边上的高_______
4.8cm
3. 满足下列条件的△ABC,不是直角三角形的是( )
A.b2=a2-c2 B. a:b:c=3:4:5
C.∠C=∠A-∠B D. ∠A:∠B : ∠C =3:4:5
D
1.若一个三角形的三边长分别为: 3, 4, x ,则此三角形是直角三角形的x的值是_____________
a. 已知Rt△
两角互余
判断是否Rt△
市民中心旁边有一块地,
已知,AD=4m,CD=3m,∠ADC=90°
AB=13m,BC=12m。求这块地的面积。
D
C
A
B
Rt△勾
股定理
Rt△的判定
5
AC=5
作业题3.如图,一个三角形窗台△ABC,
AB=4,BC=2,BD=1,CD=
判断下列结论是否正确,并说明理由
(1) CD ⊥AB;
(2) AC⊥BC
作业题3.如图在△ABC中AB=4,BC=2,BD=1,CD=
判断图中的直角三角形,并说明理由
解(1)∵BC2=BD2 +CD2=4
(2)∵AC2=AD2+CD2=12
∴∠CDB=90°
∴CD⊥AB
AC2+BC2=16=AB2
∴∠ACB=90°
∴AC⊥BC
课内练习2.如图,以△ABC的每一条边为边作三个正方形.已知这三个正方形构成的图形中,绿色部分的面积与蓝色部分的面积相等,则△ABC是直角三角形吗?请证明你的判断
是.证明:因为图中绿色部分的面积等于蓝色部分的面积, 表明两个较小正方形的面积之和等于最大正方形的面积,也就是△ABC两条较短的边的平方和等于最长边的平方,所以△ABC是Rt△(如果三角形中两边的平方和等于第三边的平方, 那么这个三角形是直角三角形).
如果
那么
有一个角是直角的三角形是直三角形
有两个角互余的三角形是直角三角形
数
形
一、边
二、角
--------直角三角形的判定
(1)有一个角是直角 的三角形是直角三角形;
(2)有两个角的和是90°的三角形是直角三角形;
角
一个三角形满足什么条件时,能判定它是直角三角形?
大约在公元前2700年,古埃及人已经建成了世界闻名的七十多座大大小小的金字塔。当时的生产工具很落后,没有直角三角板,更没有任何的先进的测量仪器。可是,这些金字塔的塔基却都是正方形,这确实是个谜?古埃及人是用什么方法得到直角呢?
《几何原本》记载了真象
他们用13个等距的结将一根绳子分成等长的12段,一个工匠同时握住绳子的第1个和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就得到一个直角三角形,其直角在第4个结处。
这其中藏
着怎样的
奥秘呢?
3
4
5
1.画一画:画出边长分别是下列各组数的三角形(单位:厘米) :
①6, 8, 10; ② 2.5 , 6, 6.5.
2.测一测:用量角器分别测量一下上述各三角形的最大度数:
1:_______ 2:_______
3.判断:请判断一下上述你所画的三角形的形状.
A:______ B:_______
直角三角形
直角三角形
5.猜想:
4.找一找:寻找三角形三边之间的关系.
如果三角形中有两边的平方和等于第三边的平方,那么这个三角形是直角三角形
36,64,100
36+64=100
各边的平方
规律
6.25,36,42.25
6.25+36=42.25
.
三边
6 8 10
2.5 6 6.5
a b c
a
c
b
A
C
B
已知:在△ABC中,三边长分别为a,b,c,且a2+b2=c2.
求证: △ABC是直角三角形.
这种方法我们把它叫做同一法
如果三角形中 有两边的平方和 等于第三边的平方,那么这个三角形是直角三角形.
数
形
最长边所对的角是直角
那直角的位
置该如何确
定呢?
较短两边的平方和
最长边的平方
根据下列条件,分别判断以a,b,c为边的△ABC是不是直角三角形,如果是,指出哪条边所对的角是直角.
(1)a=7,b=24,c=25;
(2) a:b:c=
1、先求各边的平方
2、观察较短两边的平方和与最长边的平方
3、判断是否相等
下面以a,b,c为边长且所对角分别为∠A ∠B ,∠C的三角形是不是直角三角形?如果是那么哪一个角是直角?
(2)a=7n, b=25n, c=24n (n为正整数);
(1) a= b= 2 c= ;
____ _______;
是
∠ A=90°
是
∠ B=90°
是
∠ C=90°
a=m2-n2,b=2mn,c=m2+n2 (m>n,m,n是正整数)
2.小蒋要求△ABC的的最长边上的高,测得AB=8cm,
AC=6cm,BC=10cm。则可知最长边上的高_______
4.8cm
3. 满足下列条件的△ABC,不是直角三角形的是( )
A.b2=a2-c2 B. a:b:c=3:4:5
C.∠C=∠A-∠B D. ∠A:∠B : ∠C =3:4:5
D
1.若一个三角形的三边长分别为: 3, 4, x ,则此三角形是直角三角形的x的值是_____________
a. 已知Rt△
两角互余
判断是否Rt△
市民中心旁边有一块地,
已知,AD=4m,CD=3m,∠ADC=90°
AB=13m,BC=12m。求这块地的面积。
D
C
A
B
Rt△勾
股定理
Rt△的判定
5
AC=5
作业题3.如图,一个三角形窗台△ABC,
AB=4,BC=2,BD=1,CD=
判断下列结论是否正确,并说明理由
(1) CD ⊥AB;
(2) AC⊥BC
作业题3.如图在△ABC中AB=4,BC=2,BD=1,CD=
判断图中的直角三角形,并说明理由
解(1)∵BC2=BD2 +CD2=4
(2)∵AC2=AD2+CD2=12
∴∠CDB=90°
∴CD⊥AB
AC2+BC2=16=AB2
∴∠ACB=90°
∴AC⊥BC
课内练习2.如图,以△ABC的每一条边为边作三个正方形.已知这三个正方形构成的图形中,绿色部分的面积与蓝色部分的面积相等,则△ABC是直角三角形吗?请证明你的判断
是.证明:因为图中绿色部分的面积等于蓝色部分的面积, 表明两个较小正方形的面积之和等于最大正方形的面积,也就是△ABC两条较短的边的平方和等于最长边的平方,所以△ABC是Rt△(如果三角形中两边的平方和等于第三边的平方, 那么这个三角形是直角三角形).
如果
那么
有一个角是直角的三角形是直三角形
有两个角互余的三角形是直角三角形
数
形
一、边
二、角
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
