2019-2020浙教版八年级数学上册第一章三角形的初步认识单元检查题(含答案)
文档属性
| 名称 | 2019-2020浙教版八年级数学上册第一章三角形的初步认识单元检查题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 533.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-21 15:38:12 | ||
图片预览


文档简介
2019-2020浙教版八年级数学上册第一章三角形的初步认识单元检查题
一、选择题(每小题3分,共30分)
1.已知AB=1.5,AC=4.5,若BC的长为整数,则BC的长为( )
A.3 B.6 C.3或6 D.3或4或5或6
2.一个三角形三个内角的度数之比为2∶3∶5,这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
3.下列各组线段中,能组成三角形的是( )
A. a=6.3,b=6.3,c=12.6
B. a=1,b=2,c=3
C. a=2.5,b=3,c=5
D. a=5,b=7,c=15
4.如图,△ABC的平分线AD与中线BE交于点O,有下列结论:
①AO是△ABE的角平分线;②BO是△ABD的中线,
下列说法正确的是( )
A.①②都正确 B.①不正确,②正确
C.①②都不正确 D.①正确,②不正确
5.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( )
A.20° B.30° C.35° D.40°
6.要测量河两岸的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再作出BF的垂线DE,使A,C,E在同一条直线上(如图),可以证明△ABC≌△EDC,得ED=AB,因此,测得DE的长就是AB的长.在这里判定△ABC≌△EDC的条件是( )
A.ASA B.SAS C.SSS D.以上答案均不正确
如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,
∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,
∠B=∠E.其中能使△ABC≌△DEF的条件共有( )
A.1组 B.2组 C.3组 D.4组
8.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是( )
A.3 B.4 C.6 D.5
9.如图,在锐角三角形ABC中,直线l为BC的中垂线,射线m为∠ABC的角平分线,直线l与m相交于点P.若∠BAC=60°,∠ACP=24°,则∠ABP的度数是( )
A.24° B.30° C.32° D.36°
10.两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB.小明在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=AC;③△ABD≌△CBD.其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个
二、填空题(每小题4分,共24分)
11.工人师傅在做完门框后,为防止变形常常像图中所示的那样钉上两条斜拉的木条(即图中的AB,CD两根木条),这样做的依据是____________.
12.如图,在△ABC中,D,E分别是AB,AC上的点,点F在BC的延长线上,DE∥BC,若∠1=50°,∠2=110°,则∠A=____.
13.如图,△ADB≌△ECB,若∠CBD=40°,BD⊥EC,则∠D的度数为____.
14.要说明命题“若a·b=0,则a+b=0”是假命题,可举反例__________________________.
15.如图,AC与BD相交于点O,∠A=∠D,请你补充一个条件,使得△AOB≌△DOC,你补充的条件是__________________________.
16.如图,在四边形ABCD中,给出了下列三个论断:①对角线AC平分∠BAD;②CD=BC;③∠D+∠B=180°.在上述三个论断中,若以其中两个论断作为条件,另外一个论断作为结论,则可以得出____个正确的命题.
三、解答题(共66分)
17.(8分)将下列命题改写成“如果……那么……”的形式,并指出命题的条件和结论:
(1)三条边对应相等的两个三角形全等;
(2)三角形的外角等于和它不相邻的两个内角的和.
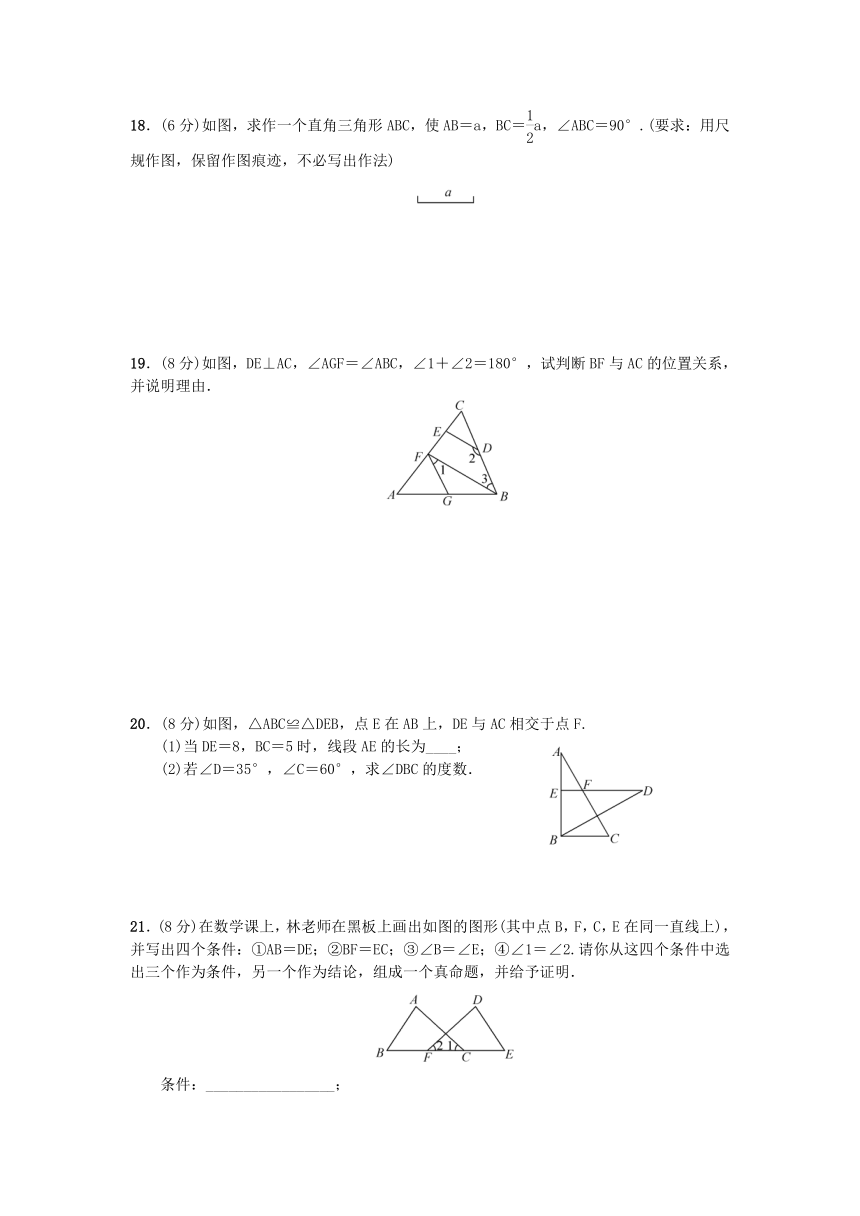
18.(6分)如图,求作一个直角三角形ABC,使AB=a,BC=a,∠ABC=90°.(要求:用尺规作图,保留作图痕迹,不必写出作法)
19.(8分)如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.
20.(8分)如图,△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=8,BC=5时,线段AE的长为____;
(2)若∠D=35°,∠C=60°,求∠DBC的度数.
21.(8分)在数学课上,林老师在黑板上画出如图的图形(其中点B,F,C,E在同一直线上),并写出四个条件:①AB=DE;②BF=EC;③∠B=∠E;④∠1=∠2.请你从这四个条件中选出三个作为条件,另一个作为结论,组成一个真命题,并给予证明.
条件:_________________;
结论:_____________.(均填写序号)
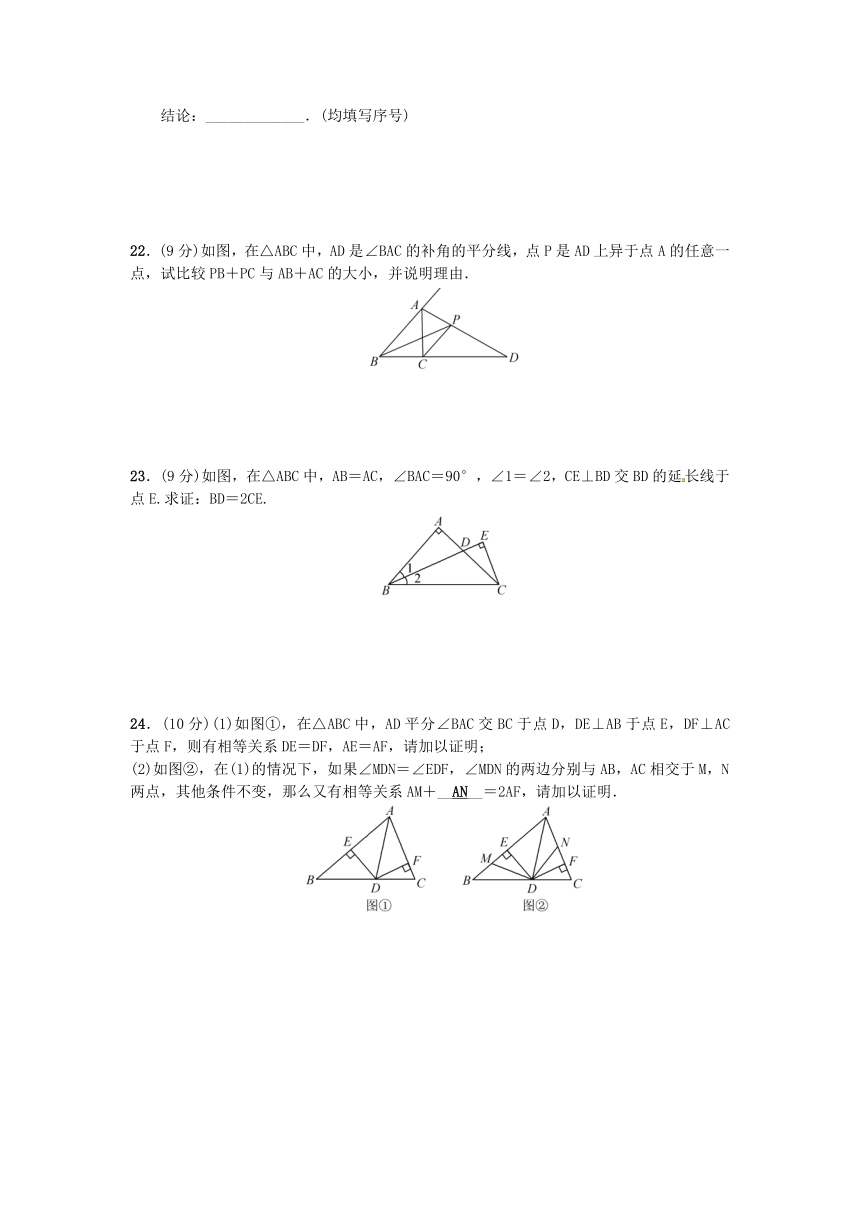
22.(9分)如图,在△ABC中,AD是∠BAC的补角的平分线,点P是AD上异于点A的任意一点,试比较PB+PC与AB+AC的大小,并说明理由.
23.(9分)如图,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E.求证:BD=2CE.
24.(10分)(1)如图①,在△ABC中,AD平分∠BAC交BC于点D,DE⊥AB于点E,DF⊥AC于点F,则有相等关系DE=DF,AE=AF,请加以证明;
(2)如图②,在(1)的情况下,如果∠MDN=∠EDF,∠MDN的两边分别与AB,AC相交于M,N两点,其他条件不变,那么又有相等关系AM+__AN__=2AF,请加以证明.
2019-2020浙教版八年级数学上册第一章三角形的初步认识单元检查题
一、选择题(每小题3分,共30分)
1.已知AB=1.5,AC=4.5,若BC的长为整数,则BC的长为( D )
A.3 B.6 C.3或6 D.3或4或5或6
2.一个三角形三个内角的度数之比为2∶3∶5,这个三角形一定是( B )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
3.下列各组线段中,能组成三角形的是(C)
A. a=6.3,b=6.3,c=12.6
B. a=1,b=2,c=3
C. a=2.5,b=3,c=5
D. a=5,b=7,c=15
4.如图,△ABC的平分线AD与中线BE交于点O,有下列结论:
①AO是△ABE的角平分线;②BO是△ABD的中线,
下列说法正确的是( D )
A.①②都正确 B.①不正确,②正确
C.①②都不正确 D.①正确,②不正确
5.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( B )
A.20° B.30° C.35° D.40°
6.要测量河两岸的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再作出BF的垂线DE,使A,C,E在同一条直线上(如图),可以证明△ABC≌△EDC,得ED=AB,因此,测得DE的长就是AB的长.在这里判定△ABC≌△EDC的条件是( A )
A.ASA B.SAS C.SSS D.以上答案均不正确
7.如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.其中能使△ABC≌△DEF的条件共有( C )
A.1组 B.2组 C.3组 D.4组
8.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是( A )
A.3 B.4 C.6 D.5
9.如图,在锐角三角形ABC中,直线l为BC的中垂线,射线m为∠ABC的角平分线,直线l与m相交于点P.若∠BAC=60°,∠ACP=24°,则∠ABP的度数是( C )
A.24° B.30° C.32° D.36°
10.两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB.小明在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=AC;③△ABD≌△CBD.其中正确的结论有( D )
A.0个 B.1个 C.2个 D.3个
二、填空题(每小题4分,共24分)
11.工人师傅在做完门框后,为防止变形常常像图中所示的那样钉上两条斜拉的木条(即图中的AB,CD两根木条),这样做的依据是__三角形的稳定性__.
12.如图,在△ABC中,D,E分别是AB,AC上的点,点F在BC的延长线上,DE∥BC,若∠1=50°,∠2=110°,则∠A=__60°__.
13.如图,△ADB≌△ECB,若∠CBD=40°,BD⊥EC,则∠D的度数为__50°__.
14.要说明命题“若a·b=0,则a+b=0”是假命题,可举反例__(-2)×0=0,但(-2)+0=-2≠0(答案不唯一)__.
15.如图,AC与BD相交于点O,∠A=∠D,请你补充一个条件,使得△AOB≌△DOC,你补充的条件是__AO=DO或AB=DC或BO=CO__.
16.如图,在四边形ABCD中,给出了下列三个论断:①对角线AC平分∠BAD;②CD=BC;③∠D+∠B=180°.在上述三个论断中,若以其中两个论断作为条件,另外一个论断作为结论,则可以得出__3__个正确的命题.
三、解答题(共66分)
17.(8分)将下列命题改写成“如果……那么……”的形式,并指出命题的条件和结论:
(1)三条边对应相等的两个三角形全等;
(2)三角形的外角等于和它不相邻的两个内角的和.
解:(1)如果两个三角形的三条边对应相等,那么这两个三角形全等;条件:两个三角形的三条边对应相等,结论:这两个三角形全等
(2)如果一个角是三角形的一个外角,那么这个角等于和它不相邻的两个内角的和;条件:一个角是三角形的一个外角,结论:这个角等于和它不相邻的两个内角的和
18.(6分)如图,求作一个直角三角形ABC,使AB=a,BC=a,∠ABC=90°.(要求:用尺规作图,保留作图痕迹,不必写出作法)
解:略
19.(8分)如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.
解:BF⊥AC.理由:∵∠AGF=∠ABC,∴FG∥BC,∴∠1=∠3.又∵∠1+∠2=180°,∴∠2+∠3=180°,∴BF∥DE.又∵DE⊥AC,∴∠DEA=90°,∴∠AFB=∠DEA=90°,∴BF⊥AC
20.(8分)如图,△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=8,BC=5时,线段AE的长为__3__;
(2)若∠D=35°,∠C=60°,求∠DBC的度数.
解:(2)∠DBC=25°
21.(8分)在数学课上,林老师在黑板上画出如图的图形(其中点B,F,C,E在同一直线上),并写出四个条件:①AB=DE;②BF=EC;③∠B=∠E;④∠1=∠2.请你从这四个条件中选出三个作为条件,另一个作为结论,组成一个真命题,并给予证明.
条件:__①②③或①③④或②③④__;
结论:__④或②或①__.(均填写序号)
证明:以题设①②③,结论④为例,∵BF=CE,∴BF+FC=CE+FC,∴BC=EF.又∵AB=DE,∠B=∠E,∴△ABC≌△DEF(SAS),∴∠1=∠2
22.(9分)如图,在△ABC中,AD是∠BAC的补角的平分线,点P是AD上异于点A的任意一点,试比较PB+PC与AB+AC的大小,并说明理由.
解:PB+PC>AB+AC.理由:在线段BA的延长线上取一点E,使AE=AC,连结PE.∵AD是∠EAC的平分线,∴∠EAP=∠CAP,可证△EAP≌△CAP(SAS),∴PE=PC,∴PB+PC=PB+PE>BE.又∵AB+AC=AB+AE=BE,∴PB+PC>AB+AC
23.(9分)如图,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E.求证:BD=2CE.
证明:分别延长BA,CE交于点F.∵BE⊥CE,∴∠BEF=∠BEC=90°.又∵∠1=∠2,BE=BE,∴△BEF≌△BEC(ASA),∴CE=FE=CF.∵∠1+∠F=90°,∠ACF+∠F=90°,∴∠1=∠ACF.又∵AB=AC,∠BAD=∠CAF=90°,∴△ABD≌△ACF(ASA),∴BD=CF,∴BD=2CE
24.(10分)(1)如图①,在△ABC中,AD平分∠BAC交BC于点D,DE⊥AB于点E,DF⊥AC于点F,则有相等关系DE=DF,AE=AF,请加以证明;
(2)如图②,在(1)的情况下,如果∠MDN=∠EDF,∠MDN的两边分别与AB,AC相交于M,N两点,其他条件不变,那么又有相等关系AM+__AN__=2AF,请加以证明.
解:(1)∵AD平分∠BAC,∴∠BAD=∠CAD.∵DE⊥AB,DF⊥AC,∴∠AED=∠AFD=90°.可证△ADE≌△ADF(AAS),∴DE=DF,AE=AF
(2)由(1)得DE=DF,∵∠MDN=∠EDF,∴∠MDE=∠NDF,可证△MDE≌△NDF(ASA),∴ME=NF,∴AM+AN=(AE+ME)+(AF-NF)=AE+AF,即AM+AN=2AF
一、选择题(每小题3分,共30分)
1.已知AB=1.5,AC=4.5,若BC的长为整数,则BC的长为( )
A.3 B.6 C.3或6 D.3或4或5或6
2.一个三角形三个内角的度数之比为2∶3∶5,这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
3.下列各组线段中,能组成三角形的是( )
A. a=6.3,b=6.3,c=12.6
B. a=1,b=2,c=3
C. a=2.5,b=3,c=5
D. a=5,b=7,c=15
4.如图,△ABC的平分线AD与中线BE交于点O,有下列结论:
①AO是△ABE的角平分线;②BO是△ABD的中线,
下列说法正确的是( )
A.①②都正确 B.①不正确,②正确
C.①②都不正确 D.①正确,②不正确
5.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( )
A.20° B.30° C.35° D.40°
6.要测量河两岸的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再作出BF的垂线DE,使A,C,E在同一条直线上(如图),可以证明△ABC≌△EDC,得ED=AB,因此,测得DE的长就是AB的长.在这里判定△ABC≌△EDC的条件是( )
A.ASA B.SAS C.SSS D.以上答案均不正确
如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,
∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,
∠B=∠E.其中能使△ABC≌△DEF的条件共有( )
A.1组 B.2组 C.3组 D.4组
8.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是( )
A.3 B.4 C.6 D.5
9.如图,在锐角三角形ABC中,直线l为BC的中垂线,射线m为∠ABC的角平分线,直线l与m相交于点P.若∠BAC=60°,∠ACP=24°,则∠ABP的度数是( )
A.24° B.30° C.32° D.36°
10.两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB.小明在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=AC;③△ABD≌△CBD.其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个
二、填空题(每小题4分,共24分)
11.工人师傅在做完门框后,为防止变形常常像图中所示的那样钉上两条斜拉的木条(即图中的AB,CD两根木条),这样做的依据是____________.
12.如图,在△ABC中,D,E分别是AB,AC上的点,点F在BC的延长线上,DE∥BC,若∠1=50°,∠2=110°,则∠A=____.
13.如图,△ADB≌△ECB,若∠CBD=40°,BD⊥EC,则∠D的度数为____.
14.要说明命题“若a·b=0,则a+b=0”是假命题,可举反例__________________________.
15.如图,AC与BD相交于点O,∠A=∠D,请你补充一个条件,使得△AOB≌△DOC,你补充的条件是__________________________.
16.如图,在四边形ABCD中,给出了下列三个论断:①对角线AC平分∠BAD;②CD=BC;③∠D+∠B=180°.在上述三个论断中,若以其中两个论断作为条件,另外一个论断作为结论,则可以得出____个正确的命题.
三、解答题(共66分)
17.(8分)将下列命题改写成“如果……那么……”的形式,并指出命题的条件和结论:
(1)三条边对应相等的两个三角形全等;
(2)三角形的外角等于和它不相邻的两个内角的和.
18.(6分)如图,求作一个直角三角形ABC,使AB=a,BC=a,∠ABC=90°.(要求:用尺规作图,保留作图痕迹,不必写出作法)
19.(8分)如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.
20.(8分)如图,△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=8,BC=5时,线段AE的长为____;
(2)若∠D=35°,∠C=60°,求∠DBC的度数.
21.(8分)在数学课上,林老师在黑板上画出如图的图形(其中点B,F,C,E在同一直线上),并写出四个条件:①AB=DE;②BF=EC;③∠B=∠E;④∠1=∠2.请你从这四个条件中选出三个作为条件,另一个作为结论,组成一个真命题,并给予证明.
条件:_________________;
结论:_____________.(均填写序号)
22.(9分)如图,在△ABC中,AD是∠BAC的补角的平分线,点P是AD上异于点A的任意一点,试比较PB+PC与AB+AC的大小,并说明理由.
23.(9分)如图,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E.求证:BD=2CE.
24.(10分)(1)如图①,在△ABC中,AD平分∠BAC交BC于点D,DE⊥AB于点E,DF⊥AC于点F,则有相等关系DE=DF,AE=AF,请加以证明;
(2)如图②,在(1)的情况下,如果∠MDN=∠EDF,∠MDN的两边分别与AB,AC相交于M,N两点,其他条件不变,那么又有相等关系AM+__AN__=2AF,请加以证明.
2019-2020浙教版八年级数学上册第一章三角形的初步认识单元检查题
一、选择题(每小题3分,共30分)
1.已知AB=1.5,AC=4.5,若BC的长为整数,则BC的长为( D )
A.3 B.6 C.3或6 D.3或4或5或6
2.一个三角形三个内角的度数之比为2∶3∶5,这个三角形一定是( B )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
3.下列各组线段中,能组成三角形的是(C)
A. a=6.3,b=6.3,c=12.6
B. a=1,b=2,c=3
C. a=2.5,b=3,c=5
D. a=5,b=7,c=15
4.如图,△ABC的平分线AD与中线BE交于点O,有下列结论:
①AO是△ABE的角平分线;②BO是△ABD的中线,
下列说法正确的是( D )
A.①②都正确 B.①不正确,②正确
C.①②都不正确 D.①正确,②不正确
5.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( B )
A.20° B.30° C.35° D.40°
6.要测量河两岸的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再作出BF的垂线DE,使A,C,E在同一条直线上(如图),可以证明△ABC≌△EDC,得ED=AB,因此,测得DE的长就是AB的长.在这里判定△ABC≌△EDC的条件是( A )
A.ASA B.SAS C.SSS D.以上答案均不正确
7.如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.其中能使△ABC≌△DEF的条件共有( C )
A.1组 B.2组 C.3组 D.4组
8.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是( A )
A.3 B.4 C.6 D.5
9.如图,在锐角三角形ABC中,直线l为BC的中垂线,射线m为∠ABC的角平分线,直线l与m相交于点P.若∠BAC=60°,∠ACP=24°,则∠ABP的度数是( C )
A.24° B.30° C.32° D.36°
10.两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB.小明在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=AC;③△ABD≌△CBD.其中正确的结论有( D )
A.0个 B.1个 C.2个 D.3个
二、填空题(每小题4分,共24分)
11.工人师傅在做完门框后,为防止变形常常像图中所示的那样钉上两条斜拉的木条(即图中的AB,CD两根木条),这样做的依据是__三角形的稳定性__.
12.如图,在△ABC中,D,E分别是AB,AC上的点,点F在BC的延长线上,DE∥BC,若∠1=50°,∠2=110°,则∠A=__60°__.
13.如图,△ADB≌△ECB,若∠CBD=40°,BD⊥EC,则∠D的度数为__50°__.
14.要说明命题“若a·b=0,则a+b=0”是假命题,可举反例__(-2)×0=0,但(-2)+0=-2≠0(答案不唯一)__.
15.如图,AC与BD相交于点O,∠A=∠D,请你补充一个条件,使得△AOB≌△DOC,你补充的条件是__AO=DO或AB=DC或BO=CO__.
16.如图,在四边形ABCD中,给出了下列三个论断:①对角线AC平分∠BAD;②CD=BC;③∠D+∠B=180°.在上述三个论断中,若以其中两个论断作为条件,另外一个论断作为结论,则可以得出__3__个正确的命题.
三、解答题(共66分)
17.(8分)将下列命题改写成“如果……那么……”的形式,并指出命题的条件和结论:
(1)三条边对应相等的两个三角形全等;
(2)三角形的外角等于和它不相邻的两个内角的和.
解:(1)如果两个三角形的三条边对应相等,那么这两个三角形全等;条件:两个三角形的三条边对应相等,结论:这两个三角形全等
(2)如果一个角是三角形的一个外角,那么这个角等于和它不相邻的两个内角的和;条件:一个角是三角形的一个外角,结论:这个角等于和它不相邻的两个内角的和
18.(6分)如图,求作一个直角三角形ABC,使AB=a,BC=a,∠ABC=90°.(要求:用尺规作图,保留作图痕迹,不必写出作法)
解:略
19.(8分)如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.
解:BF⊥AC.理由:∵∠AGF=∠ABC,∴FG∥BC,∴∠1=∠3.又∵∠1+∠2=180°,∴∠2+∠3=180°,∴BF∥DE.又∵DE⊥AC,∴∠DEA=90°,∴∠AFB=∠DEA=90°,∴BF⊥AC
20.(8分)如图,△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=8,BC=5时,线段AE的长为__3__;
(2)若∠D=35°,∠C=60°,求∠DBC的度数.
解:(2)∠DBC=25°
21.(8分)在数学课上,林老师在黑板上画出如图的图形(其中点B,F,C,E在同一直线上),并写出四个条件:①AB=DE;②BF=EC;③∠B=∠E;④∠1=∠2.请你从这四个条件中选出三个作为条件,另一个作为结论,组成一个真命题,并给予证明.
条件:__①②③或①③④或②③④__;
结论:__④或②或①__.(均填写序号)
证明:以题设①②③,结论④为例,∵BF=CE,∴BF+FC=CE+FC,∴BC=EF.又∵AB=DE,∠B=∠E,∴△ABC≌△DEF(SAS),∴∠1=∠2
22.(9分)如图,在△ABC中,AD是∠BAC的补角的平分线,点P是AD上异于点A的任意一点,试比较PB+PC与AB+AC的大小,并说明理由.
解:PB+PC>AB+AC.理由:在线段BA的延长线上取一点E,使AE=AC,连结PE.∵AD是∠EAC的平分线,∴∠EAP=∠CAP,可证△EAP≌△CAP(SAS),∴PE=PC,∴PB+PC=PB+PE>BE.又∵AB+AC=AB+AE=BE,∴PB+PC>AB+AC
23.(9分)如图,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E.求证:BD=2CE.
证明:分别延长BA,CE交于点F.∵BE⊥CE,∴∠BEF=∠BEC=90°.又∵∠1=∠2,BE=BE,∴△BEF≌△BEC(ASA),∴CE=FE=CF.∵∠1+∠F=90°,∠ACF+∠F=90°,∴∠1=∠ACF.又∵AB=AC,∠BAD=∠CAF=90°,∴△ABD≌△ACF(ASA),∴BD=CF,∴BD=2CE
24.(10分)(1)如图①,在△ABC中,AD平分∠BAC交BC于点D,DE⊥AB于点E,DF⊥AC于点F,则有相等关系DE=DF,AE=AF,请加以证明;
(2)如图②,在(1)的情况下,如果∠MDN=∠EDF,∠MDN的两边分别与AB,AC相交于M,N两点,其他条件不变,那么又有相等关系AM+__AN__=2AF,请加以证明.
解:(1)∵AD平分∠BAC,∴∠BAD=∠CAD.∵DE⊥AB,DF⊥AC,∴∠AED=∠AFD=90°.可证△ADE≌△ADF(AAS),∴DE=DF,AE=AF
(2)由(1)得DE=DF,∵∠MDN=∠EDF,∴∠MDE=∠NDF,可证△MDE≌△NDF(ASA),∴ME=NF,∴AM+AN=(AE+ME)+(AF-NF)=AE+AF,即AM+AN=2AF
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
