6.5 角与角的度量(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 6.5 角与角的度量(知识清单+经典例题+夯实基础+提优特训+中考链接) |

|
|
| 格式 | zip | ||
| 文件大小 | 488.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-23 13:25:22 | ||
图片预览


文档简介
浙江版2019-2020学年度七年级数学上册第6章图形的初步知识
6.5 角和角的度量
【知识清单】
1.从静态角度认识角:如图(1)有公共端点的两条射线组成的图形叫做角,这个公共端点叫做角的顶点,这两条射线叫做角的边.
2.从动态角度认识角:如图(2)角也可以看成是由一条射线绕着它的端点旋转而成的图形,起始位置的射线叫做角的始边,终止位置的射线叫做角的终边.
3.角的表示:角的表示法:角的符号为“∠”.
①用三个字母表示,顶点的字母必须放在中间,如图(3)所示∠AOB或∠BOA;
②用一个字母表示,在这个顶点上只有一个角,如图(3)所示∠A;
③用一个数字表示,在要表示的角的内部画弧线,如图(4)所示∠1;
④用希腊字母表示,在要表示的角的内部画弧线,如图(4)所示∠α.
4.角的性质:
①因为射线是向一方无限延伸的,所以角的两边无所谓长短,即角的大小与它的边长无关;
②角的大小可以度量.
③角可以参与运算.
5.角的基本度量单位:度“°”、分“′”、秒“″”.
6.角度数的换算:1°=60′,1′=60″.注意:相同单位逢十进一,不同单位的逢六十进一.
7.平角:如图(5)射线OA绕点O旋转,当终边OB在始边OA成一条直线时,所成的角叫做平角,一个平角等于180°;
8.周角:如图(6)射线OA绕点O旋转,当终边OB与始边OA再次重合时所成的角叫做周角,一个周角等于360°.
【经典例题】
例题1、用度、分、秒表示28.34°,正确的是( )
A. B. C. D.
【考点】度分秒的换算.
【分析】进行度、分、秒转化运算,注意以60为进制.
【解答】根据角的换算可得28.34°=28°+0.34×60′
=28°+20.4′
=28°+20′+0.4×60″
=28°20′24″.
故选B.
【点评】此类题是进行度、分、秒转化运算,相对比较简单,掌握以60为进制是解题的关键.
例题2、时钟指向2时25分时,这时时针与分针所成的锐角是______.
【考点】钟面角.?
【分析】因为钟表上的刻度是把一个圆平均分成了12等份,每一份是30°,可以推出分针每分钟转6°,时针在钟面上每分钟转0.5°,找出时针和分针之间相差的大格数进行计算即可.
【解答】∵时钟分针每分钟转6°,时针在钟面上每分钟转0.5°,
∴钟表上2点25分,时针与分针的夹角可以看成2×30°+(30°0.5°×25)=77.5°.
故答案为:77.5°.
【点评】本题考查钟表时针与分针的夹角.在钟表问题中,常利用时针与分针转动的度数关系:分针每转动6°时针转动0.5°,利用起点时间时针和分针的位置关系建立角的图形是解题是关键.
【夯实基础】
1.下列说法中,正确的个数是(??)?
①角是由两条射线组成的图形; ?②角可以看成一条射线绕着它的端点旋转而形成的图形; ?③一条直线就是一个平角;④一条射线就是一个周角;⑤角的边越长,角的度数越大.
A.1个 B.2个 C.3个 D.4个
2.图中角的个数是(? ?)?
? A.5个 B.8个
C.9个 D.10个
3.下列四个图形中,能同时用∠1,∠ABC,∠B三种方法表示同一个角的图形是(? ?)
4.下列关于角度的互化中,正确的是(??)
? A.75.3°=75°30′? B.33°24′36″=33.48°
? C.36°36′36″=36.6°? D.56.35°=56°21′
5.(1)= °, ′.
(2)若∠1=46°25′,∠2=46.5°,则∠1与∠2的大小关系是 .
(3)时钟显示为上午9时30分,时针与分针所夹角度是 .
(4)从上午7时20分到上午9时45分,时钟的时针转过的角度是 .
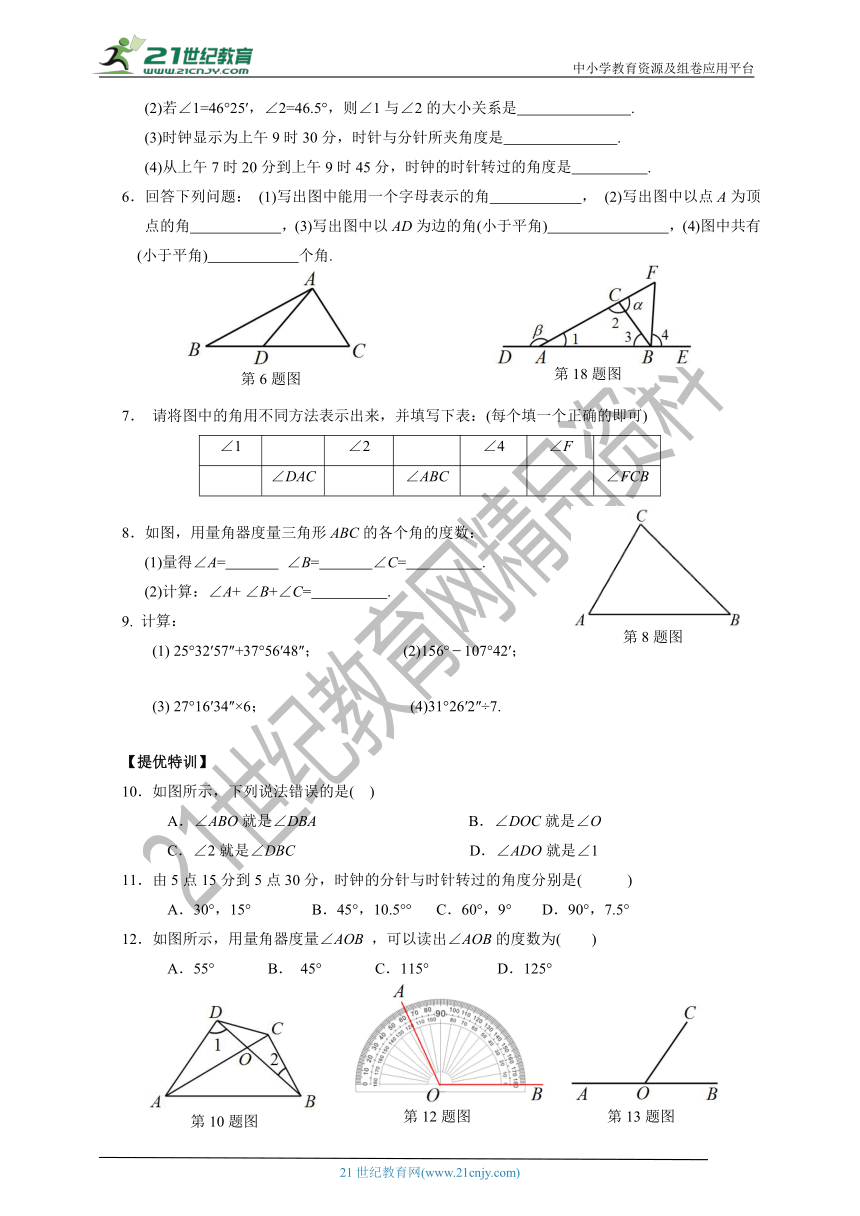
6.回答下列问题:?(1)写出图中能用一个字母表示的角 ,?(2)写出图中以点A为顶点的角 ,(3)写出图中以AD为边的角(小于平角) ?,(4)图中共有
(小于平角) 个角.?
7. 请将图中的角用不同方法表示出来,并填写下表:(每个填一个正确的即可)
∠1
∠2
∠4
∠F
∠DAC
∠ABC
∠FCB
8.如图,用量角器度量三角形ABC的各个角的度数:
(1)量得∠A= ∠B= ∠C= .
(2)计算:∠A+ ∠B+∠C= .
9. 计算:
(1) 25°32′57″+37°56′48″; (2)156°107°42′;
(3) 27°16′34″×6; (4)31°26′2″÷7.
【提优特训】
10.如图所示,下列说法错误的是(??)?
? A.∠ABO就是∠DBA??? B.∠DOC就是∠O?
C.∠2就是∠DBC??? D.∠ADO就是∠1
11.由5点15分到5点30分,时钟的分针与时针转过的角度分别是(? ?)
? A.30°,15° ? ?B.45°,10.5°? ?C.60°,9° ??D.90°,7.5°
12.如图所示,用量角器度量∠AOB ,可以读出∠AOB的度数为( )
A.55° B. 45° C.115° D.125°
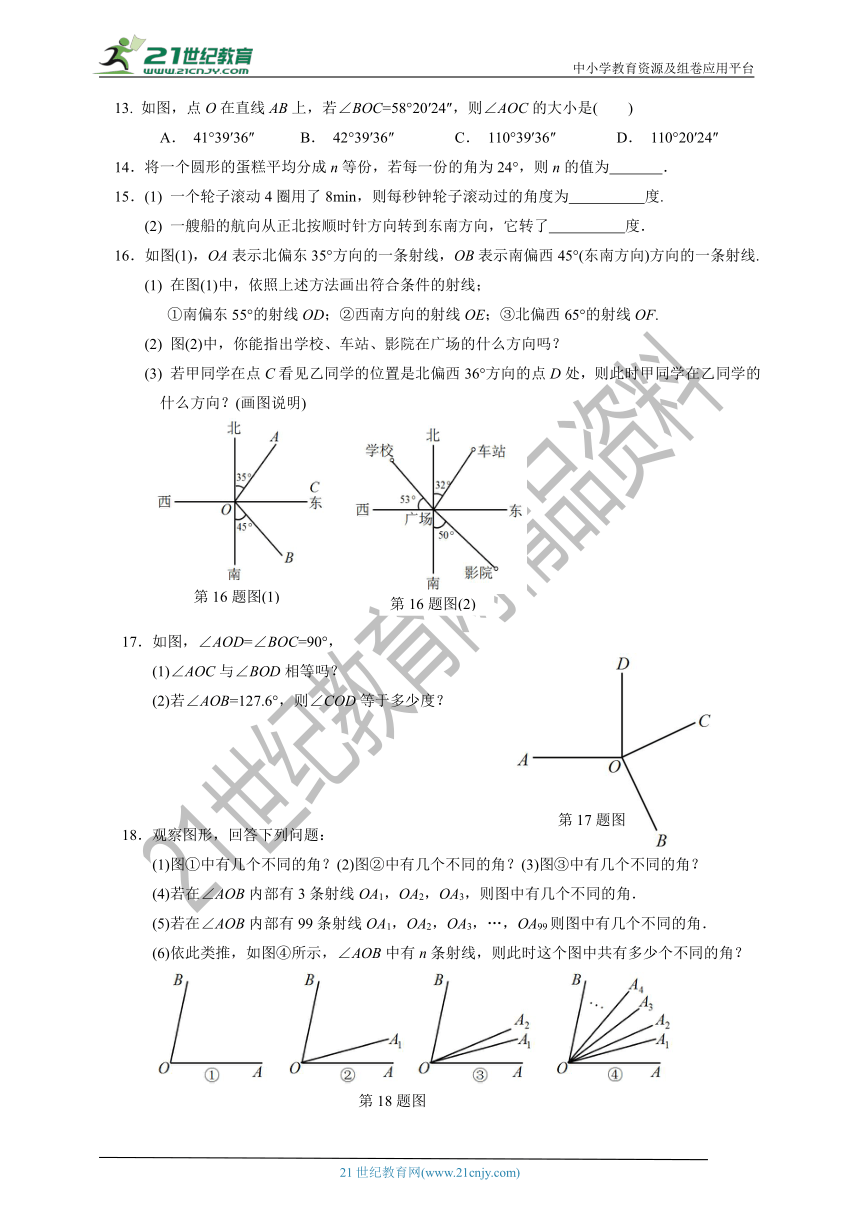
13. 如图,点O在直线AB上,若∠BOC=58°20′24″,则∠AOC的大小是( )
A. 41°39′36″ B. 42°39′36″ C. 110°39′36″ D. 110°20′24″
14.将一个圆形的蛋糕平均分成n等份,若每一份的角为24°,则n的值为 .
15.(1) 一个轮子滚动4圈用了8min,则每秒钟轮子滚动过的角度为 度.
(2) 一艘船的航向从正北按顺时针方向转到东南方向,它转了 度.
16.如图(1),OA表示北偏东35°方向的一条射线,OB表示南偏西45°(东南方向)方向的一条射线.
(1) 在图(1)中,依照上述方法画出符合条件的射线;
①南偏东55°的射线OD;②西南方向的射线OE;③北偏西65°的射线OF.
(2) 图(2)中,你能指出学校、车站、影院在广场的什么方向吗?
(3) 若甲同学在点C看见乙同学的位置是北偏西36°方向的点D处,则此时甲同学在乙同学的
什么方向?(画图说明)
17.如图,∠AOD=∠BOC=90°,
(1)∠AOC与∠BOD相等吗?
(2)若∠AOB=127.6°,则∠COD等于多少度?
18.观察图形,回答下列问题:
(1)图①中有几个不同的角?(2)图②中有几个不同的角?(3)图③中有几个不同的角?
(4)若在∠AOB内部有3条射线OA1,OA2,OA3,则图中有几个不同的角.
(5)若在∠AOB内部有99条射线OA1,OA2,OA3,…,OA99则图中有几个不同的角.
(6)依此类推,如图④所示,∠AOB中有n条射线,则此时这个图中共有多少个不同的角?
19.如图,有一张地图,点 A、B、C代表三地,但是已被墨迹污染,C地具体位置看不清楚了.但是知道C地在A地的南偏西45°,在B地的北偏西52°,请你确定C地的位置.
20.(1) 作一个四边形ABCD,分别量得∠A= °,∠B= °, ∠C= °,∠D= °,计算∠A+∠B+∠C+∠D= °.
(2) 再作另一个四边形EFGH,分别量得∠E= °,∠F= °, ∠G= °,
∠H= °,计算∠E+∠F+∠G+∠H= °.
(3) 综合(1)(2)你有什么猜想?请你把他写出来.
21.某人下午6点多多一点出门时,抬头看了一下时钟上的时针和分针的夹角恰为110°,等他回来以后,发现表上的时针和分针的夹角仍是110°,且还播放〈新闻联播〉,试算一算此人外出共用了多长时间.
【中考链接】
22.(2019?模拟) 钟面角是指时钟的时针与分针所成的角,如果时间从下午1点整到下午4点整,钟面角为90°的情况有( )
A.有一种 B.有四种 C.有五种 D.有六种
23.(2019?模拟)如图,OA的方向是北偏东25°,OB的方向是北偏西35°,若∠AOB=∠AOC,则OC的方向是 .
参考答案
1、A 2、D 3、B 4、D 5.(1)17 ,45 (2) ∠1<∠2 (3) 105° (4)72.5°
6、(1) ∠B , ∠C (2) ∠BAD或∠DAB, ∠DAC或∠CAD, ∠BAC或∠CAB, (3) ∠BAD或∠DAB, ∠DAC或∠CAD, ∠ADB或∠BDA, ∠ADC或∠CDA, (4)7. 7、用三个字母表示角不唯一:
∠1
∠β
∠2
∠3
∠4
∠F
∠α
∠BAC
∠DAC
∠ACB
∠ABC
∠FBE
∠AFB
∠FCB
10、B 11、D 12、C 13、C 14、15 15、(1) 3 ,(2) 135 22、C 23、北偏东75°
8.如图,用量角器度量三角形ABC的各个角的度数:
(1)量得∠A= 60° ,∠B= 45° ,∠C= 75° .
(2)计算:∠A+ ∠B+∠C= 180° .
9. 解:(1)原式=62°88′105″=63°29′45″;
(2)原式=155°60′107°42′=48°18′;
(3)原式=27°×6+16′×6+34″×6
=162°+96′+204″
=163°37′24″;
(4)原式=28°÷7+203′÷7+182″÷7
=4°+29′+26″=4°29′26″.
16.解:(1)如图(3)是所作图形:
(2)学校在广场的北偏西37°的方向上,
车站在广场的北偏东32°的方向上,
影院在广场的南偏东50°的方向上.
(3)南偏东36°的方向上如图(4).
17.解:(1)相等:
∠AOD=∠BOC
∠AOD+∠COD =∠BOC+∠COD
∠AOC=∠BOD.
(2) ∠AOB+∠BOC+∠COD+∠DOA=360°,
∠AOD=∠BOC=90°,
∠AOB +∠COD =360°(∠AOD+∠BOC)=180°.
∠COD=180°∠AOB=180°127.6°=52.4°.
18. 解:(1) 图①只有一个角.
(2) 图②在∠AOB内部有1条射线OA1,则图中有1+2=3(个)不同的角.
?(3) 图②在∠AOB内部有2条射线OA1,OA2,则图中有1+2+3= 6(个)不同的角.
(4)在∠AOB内部有3条射线OA1,OA2,OA3,则图中有1+2+3+4=10(个)不同的角.?
(5)在∠AOB内部有99条射线OA1,OA2,OA3,…,OA99,
则图中有1+2+3+…+99+100=5050(个)不同的角.
(6)在∠AOB内部画n条射线OA1,OA2,OA3,…,OAn,
则图中有1+2+3+…+n+(n+1) = (个) 不同的角.
19.解:如图,过点A画出南偏西45°的射线AC,
过点B画出北偏西52°的射线BC,
其交点就是确定的C地的位置.
20.解:(1) (2)因为所画四边形不同得到的各角的度数不可能相同,
但是∠A+∠B+∠C+∠D=360°,∠E+∠F+∠G+∠H=360°.
(3)四边形四个内角之和等于360°.
21.解:我们知道钟表的表盘是360°,共分成12个大格,时针12小时转动一圈,所以每个小时转动30°,每分钟转动0.5°.分针一个小时转动360°,每分钟转动6°.因为此人离开家不到一个小时,所以肯定是六点初离开家,快到7点回到家,这个过程中出现过2次时针与分针的夹角为110°的情况.
情况1,设出门时,已经是6点整过了x分钟,时针与分针指向数字12时的夹角大于180°,其度数为180°+(0.5x)°,与此同时,分针与分针指向数字12时的夹角为(6x)°.
因为两针夹角为110°,根据题意可列方程180+0.5x6x=110,解得x=.
情况2,设返回家时,时间为6点y分,夹角又为110°,
可列方程6y(180+0.5y)=110,解得y=.?
yx=40,?
所以此人外出共用了40分钟.
6.5 角和角的度量
【知识清单】
1.从静态角度认识角:如图(1)有公共端点的两条射线组成的图形叫做角,这个公共端点叫做角的顶点,这两条射线叫做角的边.
2.从动态角度认识角:如图(2)角也可以看成是由一条射线绕着它的端点旋转而成的图形,起始位置的射线叫做角的始边,终止位置的射线叫做角的终边.
3.角的表示:角的表示法:角的符号为“∠”.
①用三个字母表示,顶点的字母必须放在中间,如图(3)所示∠AOB或∠BOA;
②用一个字母表示,在这个顶点上只有一个角,如图(3)所示∠A;
③用一个数字表示,在要表示的角的内部画弧线,如图(4)所示∠1;
④用希腊字母表示,在要表示的角的内部画弧线,如图(4)所示∠α.
4.角的性质:
①因为射线是向一方无限延伸的,所以角的两边无所谓长短,即角的大小与它的边长无关;
②角的大小可以度量.
③角可以参与运算.
5.角的基本度量单位:度“°”、分“′”、秒“″”.
6.角度数的换算:1°=60′,1′=60″.注意:相同单位逢十进一,不同单位的逢六十进一.
7.平角:如图(5)射线OA绕点O旋转,当终边OB在始边OA成一条直线时,所成的角叫做平角,一个平角等于180°;
8.周角:如图(6)射线OA绕点O旋转,当终边OB与始边OA再次重合时所成的角叫做周角,一个周角等于360°.
【经典例题】
例题1、用度、分、秒表示28.34°,正确的是( )
A. B. C. D.
【考点】度分秒的换算.
【分析】进行度、分、秒转化运算,注意以60为进制.
【解答】根据角的换算可得28.34°=28°+0.34×60′
=28°+20.4′
=28°+20′+0.4×60″
=28°20′24″.
故选B.
【点评】此类题是进行度、分、秒转化运算,相对比较简单,掌握以60为进制是解题的关键.
例题2、时钟指向2时25分时,这时时针与分针所成的锐角是______.
【考点】钟面角.?
【分析】因为钟表上的刻度是把一个圆平均分成了12等份,每一份是30°,可以推出分针每分钟转6°,时针在钟面上每分钟转0.5°,找出时针和分针之间相差的大格数进行计算即可.
【解答】∵时钟分针每分钟转6°,时针在钟面上每分钟转0.5°,
∴钟表上2点25分,时针与分针的夹角可以看成2×30°+(30°0.5°×25)=77.5°.
故答案为:77.5°.
【点评】本题考查钟表时针与分针的夹角.在钟表问题中,常利用时针与分针转动的度数关系:分针每转动6°时针转动0.5°,利用起点时间时针和分针的位置关系建立角的图形是解题是关键.
【夯实基础】
1.下列说法中,正确的个数是(??)?
①角是由两条射线组成的图形; ?②角可以看成一条射线绕着它的端点旋转而形成的图形; ?③一条直线就是一个平角;④一条射线就是一个周角;⑤角的边越长,角的度数越大.
A.1个 B.2个 C.3个 D.4个
2.图中角的个数是(? ?)?
? A.5个 B.8个
C.9个 D.10个
3.下列四个图形中,能同时用∠1,∠ABC,∠B三种方法表示同一个角的图形是(? ?)
4.下列关于角度的互化中,正确的是(??)
? A.75.3°=75°30′? B.33°24′36″=33.48°
? C.36°36′36″=36.6°? D.56.35°=56°21′
5.(1)= °, ′.
(2)若∠1=46°25′,∠2=46.5°,则∠1与∠2的大小关系是 .
(3)时钟显示为上午9时30分,时针与分针所夹角度是 .
(4)从上午7时20分到上午9时45分,时钟的时针转过的角度是 .
6.回答下列问题:?(1)写出图中能用一个字母表示的角 ,?(2)写出图中以点A为顶点的角 ,(3)写出图中以AD为边的角(小于平角) ?,(4)图中共有
(小于平角) 个角.?
7. 请将图中的角用不同方法表示出来,并填写下表:(每个填一个正确的即可)
∠1
∠2
∠4
∠F
∠DAC
∠ABC
∠FCB
8.如图,用量角器度量三角形ABC的各个角的度数:
(1)量得∠A= ∠B= ∠C= .
(2)计算:∠A+ ∠B+∠C= .
9. 计算:
(1) 25°32′57″+37°56′48″; (2)156°107°42′;
(3) 27°16′34″×6; (4)31°26′2″÷7.
【提优特训】
10.如图所示,下列说法错误的是(??)?
? A.∠ABO就是∠DBA??? B.∠DOC就是∠O?
C.∠2就是∠DBC??? D.∠ADO就是∠1
11.由5点15分到5点30分,时钟的分针与时针转过的角度分别是(? ?)
? A.30°,15° ? ?B.45°,10.5°? ?C.60°,9° ??D.90°,7.5°
12.如图所示,用量角器度量∠AOB ,可以读出∠AOB的度数为( )
A.55° B. 45° C.115° D.125°
13. 如图,点O在直线AB上,若∠BOC=58°20′24″,则∠AOC的大小是( )
A. 41°39′36″ B. 42°39′36″ C. 110°39′36″ D. 110°20′24″
14.将一个圆形的蛋糕平均分成n等份,若每一份的角为24°,则n的值为 .
15.(1) 一个轮子滚动4圈用了8min,则每秒钟轮子滚动过的角度为 度.
(2) 一艘船的航向从正北按顺时针方向转到东南方向,它转了 度.
16.如图(1),OA表示北偏东35°方向的一条射线,OB表示南偏西45°(东南方向)方向的一条射线.
(1) 在图(1)中,依照上述方法画出符合条件的射线;
①南偏东55°的射线OD;②西南方向的射线OE;③北偏西65°的射线OF.
(2) 图(2)中,你能指出学校、车站、影院在广场的什么方向吗?
(3) 若甲同学在点C看见乙同学的位置是北偏西36°方向的点D处,则此时甲同学在乙同学的
什么方向?(画图说明)
17.如图,∠AOD=∠BOC=90°,
(1)∠AOC与∠BOD相等吗?
(2)若∠AOB=127.6°,则∠COD等于多少度?
18.观察图形,回答下列问题:
(1)图①中有几个不同的角?(2)图②中有几个不同的角?(3)图③中有几个不同的角?
(4)若在∠AOB内部有3条射线OA1,OA2,OA3,则图中有几个不同的角.
(5)若在∠AOB内部有99条射线OA1,OA2,OA3,…,OA99则图中有几个不同的角.
(6)依此类推,如图④所示,∠AOB中有n条射线,则此时这个图中共有多少个不同的角?
19.如图,有一张地图,点 A、B、C代表三地,但是已被墨迹污染,C地具体位置看不清楚了.但是知道C地在A地的南偏西45°,在B地的北偏西52°,请你确定C地的位置.
20.(1) 作一个四边形ABCD,分别量得∠A= °,∠B= °, ∠C= °,∠D= °,计算∠A+∠B+∠C+∠D= °.
(2) 再作另一个四边形EFGH,分别量得∠E= °,∠F= °, ∠G= °,
∠H= °,计算∠E+∠F+∠G+∠H= °.
(3) 综合(1)(2)你有什么猜想?请你把他写出来.
21.某人下午6点多多一点出门时,抬头看了一下时钟上的时针和分针的夹角恰为110°,等他回来以后,发现表上的时针和分针的夹角仍是110°,且还播放〈新闻联播〉,试算一算此人外出共用了多长时间.
【中考链接】
22.(2019?模拟) 钟面角是指时钟的时针与分针所成的角,如果时间从下午1点整到下午4点整,钟面角为90°的情况有( )
A.有一种 B.有四种 C.有五种 D.有六种
23.(2019?模拟)如图,OA的方向是北偏东25°,OB的方向是北偏西35°,若∠AOB=∠AOC,则OC的方向是 .
参考答案
1、A 2、D 3、B 4、D 5.(1)17 ,45 (2) ∠1<∠2 (3) 105° (4)72.5°
6、(1) ∠B , ∠C (2) ∠BAD或∠DAB, ∠DAC或∠CAD, ∠BAC或∠CAB, (3) ∠BAD或∠DAB, ∠DAC或∠CAD, ∠ADB或∠BDA, ∠ADC或∠CDA, (4)7. 7、用三个字母表示角不唯一:
∠1
∠β
∠2
∠3
∠4
∠F
∠α
∠BAC
∠DAC
∠ACB
∠ABC
∠FBE
∠AFB
∠FCB
10、B 11、D 12、C 13、C 14、15 15、(1) 3 ,(2) 135 22、C 23、北偏东75°
8.如图,用量角器度量三角形ABC的各个角的度数:
(1)量得∠A= 60° ,∠B= 45° ,∠C= 75° .
(2)计算:∠A+ ∠B+∠C= 180° .
9. 解:(1)原式=62°88′105″=63°29′45″;
(2)原式=155°60′107°42′=48°18′;
(3)原式=27°×6+16′×6+34″×6
=162°+96′+204″
=163°37′24″;
(4)原式=28°÷7+203′÷7+182″÷7
=4°+29′+26″=4°29′26″.
16.解:(1)如图(3)是所作图形:
(2)学校在广场的北偏西37°的方向上,
车站在广场的北偏东32°的方向上,
影院在广场的南偏东50°的方向上.
(3)南偏东36°的方向上如图(4).
17.解:(1)相等:
∠AOD=∠BOC
∠AOD+∠COD =∠BOC+∠COD
∠AOC=∠BOD.
(2) ∠AOB+∠BOC+∠COD+∠DOA=360°,
∠AOD=∠BOC=90°,
∠AOB +∠COD =360°(∠AOD+∠BOC)=180°.
∠COD=180°∠AOB=180°127.6°=52.4°.
18. 解:(1) 图①只有一个角.
(2) 图②在∠AOB内部有1条射线OA1,则图中有1+2=3(个)不同的角.
?(3) 图②在∠AOB内部有2条射线OA1,OA2,则图中有1+2+3= 6(个)不同的角.
(4)在∠AOB内部有3条射线OA1,OA2,OA3,则图中有1+2+3+4=10(个)不同的角.?
(5)在∠AOB内部有99条射线OA1,OA2,OA3,…,OA99,
则图中有1+2+3+…+99+100=5050(个)不同的角.
(6)在∠AOB内部画n条射线OA1,OA2,OA3,…,OAn,
则图中有1+2+3+…+n+(n+1) = (个) 不同的角.
19.解:如图,过点A画出南偏西45°的射线AC,
过点B画出北偏西52°的射线BC,
其交点就是确定的C地的位置.
20.解:(1) (2)因为所画四边形不同得到的各角的度数不可能相同,
但是∠A+∠B+∠C+∠D=360°,∠E+∠F+∠G+∠H=360°.
(3)四边形四个内角之和等于360°.
21.解:我们知道钟表的表盘是360°,共分成12个大格,时针12小时转动一圈,所以每个小时转动30°,每分钟转动0.5°.分针一个小时转动360°,每分钟转动6°.因为此人离开家不到一个小时,所以肯定是六点初离开家,快到7点回到家,这个过程中出现过2次时针与分针的夹角为110°的情况.
情况1,设出门时,已经是6点整过了x分钟,时针与分针指向数字12时的夹角大于180°,其度数为180°+(0.5x)°,与此同时,分针与分针指向数字12时的夹角为(6x)°.
因为两针夹角为110°,根据题意可列方程180+0.5x6x=110,解得x=.
情况2,设返回家时,时间为6点y分,夹角又为110°,
可列方程6y(180+0.5y)=110,解得y=.?
yx=40,?
所以此人外出共用了40分钟.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
