第三章 圆的基本性质 章末检测（解析版）

初中数学浙教版九年级上册第三章 圆的基本性质 章末检测
一、单选题
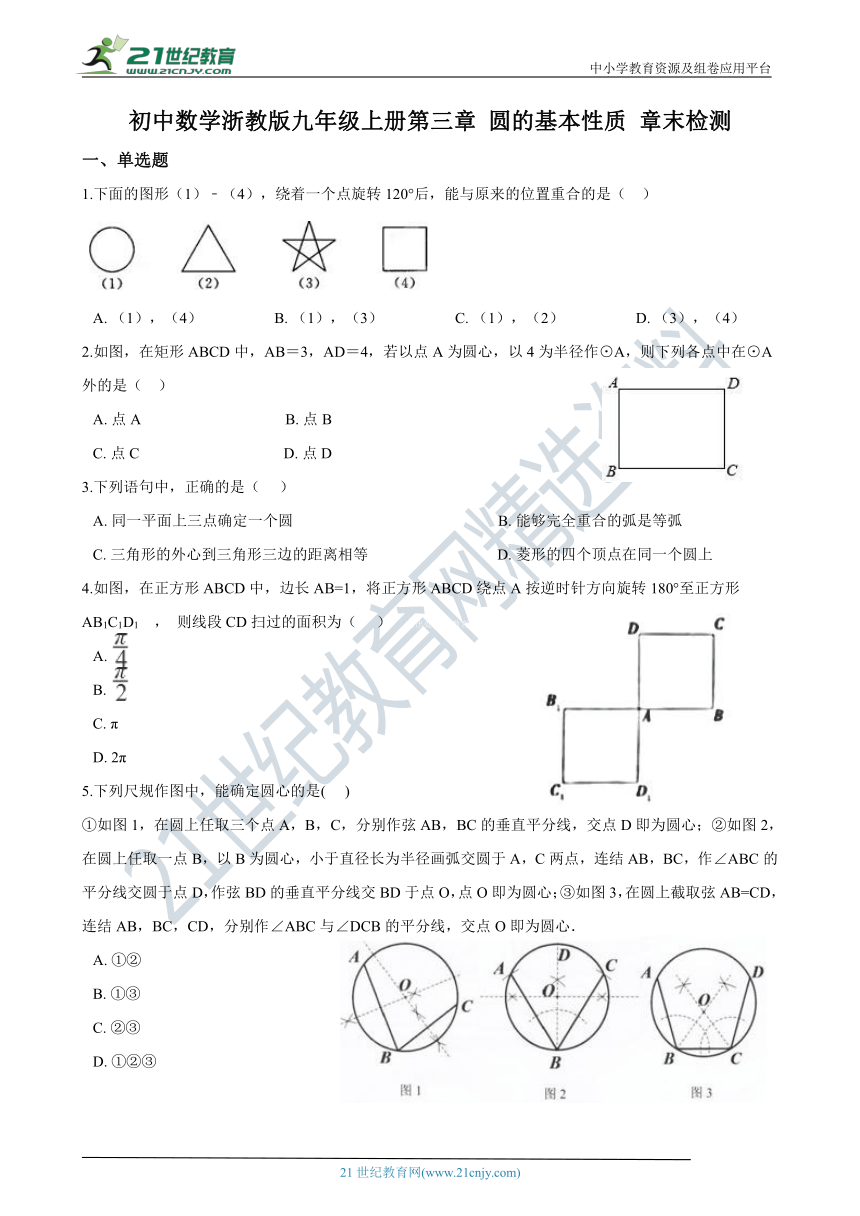
1.下面的图形（1）﹣（4），绕着一个点旋转120°后，能与原来的位置重合的是（?? ）

A.?（1），（4）??????????????? ??B.?（1），（3）??????????????? ??C.?（1），（2）???????? ?????????D.?（3），（4）
2.如图，在矩形ABCD中，AB＝3，AD＝4，若以点A为圆心，以4为半径作⊙A，则下列各点中在⊙A外的是（?? ） 21教育网
A.?点A??????????????????????????????????????B.?点B??????????????????????????????????????
C.?点C??????????????????????????????????????D.?点D
3.下列语句中，正确的是（ ???）
A.?同一平面上三点确定一个圆 B.?能够完全重合的弧是等弧C.?三角形的外心到三角形三边的距离相等 D.?菱形的四个顶点在同一个圆上2·1·c·n·j·y
4.如图，在正方形ABCD中，边长AB=1，将正方形ABCD绕点A按逆时针方向旋转180°至正方形AB1C1D1 ， 则线段CD扫过的面积为（??? ） 【出处：21教育名师】
A.??????????????????????????????????????????
B.??????????????????????????????????????????
C.?π?????????????????????????????????????????
D.?2π
5.下列尺规作图中，能确定圆心的是(??? )
①如图1，在圆上任取三个点A，B，C，分别作弦AB，BC的垂直平分线，交点D即为圆心；②如图2，在圆上任取一点B，以B为圆心，小于直径长为半径画弧交圆于A，C两点，连结AB，BC，作∠ABC的平分线交圆于点D，作弦BD的垂直平分线交BD于点O，点O即为圆心；③如图3，在圆上截取弦AB=CD，连结AB，BC，CD，分别作∠ABC与∠DCB的平分线，交点O即为圆心．21教育名师原创作品
A.?①②????????????????????????????????????
B.?①③????????????????????????????????????
C.?②③????????????????????????????????????
D.?①②③
6.如图，在⊙O中，若点C是 的中点，∠A=50°，则∠BOC=( ???)
A.?40°???????????????????????????????????????
B.?45°???????????????????????????????????????
C.?50°???????????????????????????????????????
D.?60°
7.如图，点 在圆上，若弦 的长度等于圆半径的 倍，则 的度数是(??? ).
A.?22.5°??????????????????????????????????????
B.?30°??????????????????????????????????????
C.?45°??????????????????????????????????????
D.?60°
8.如图，四边形ABCD是 的内接四边形，若 ，则 的度数是 ??
A.???????????????????????????????????????
B.???????????????????????????????????????
C.??????????????????????????????????????
D.?
9.圆内接正六边形的周长为24，则该圆的内接正三角形的周长为（?? ）
A.?12 ?????????????????????????????????????B.?6 ?????????????????????????????????????C.?12?????????????????????????????????????D.?6
10.如图，正方形ABCD内接于⊙O，AB=2 ，则 的长是（?? ）
A.?π???????????????????????????????????????
B.?π???????????????????????????????????????
C.?2π???????????????????????????????????????
D.?π
二、填空题
11.正n边形的一个内角为120°，则n的值为________.
12.如图，△ABC的外接圆的圆心坐标为________．

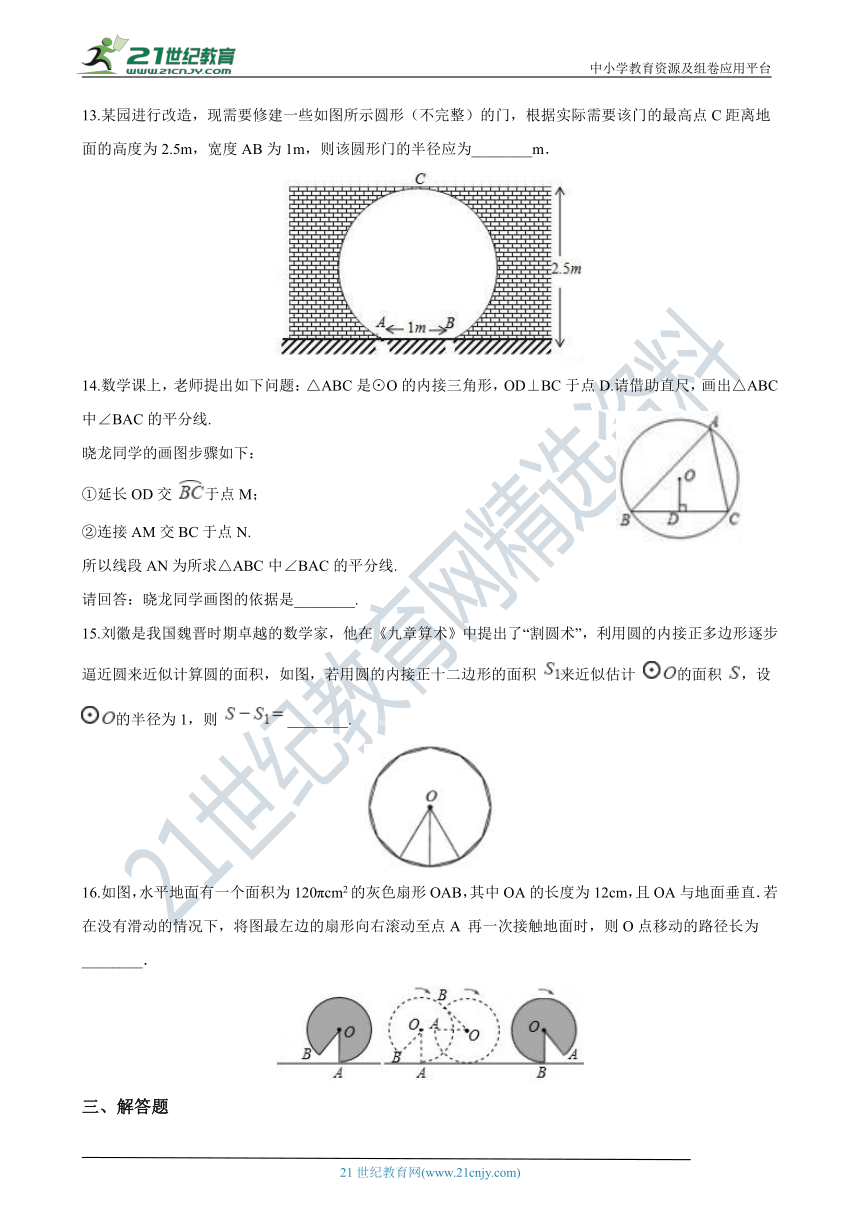
13.某园进行改造，现需要修建一些如图所示圆形（不完整）的门，根据实际需要该门的最高点C距离地面的高度为2.5m，宽度AB为1m，则该圆形门的半径应为________m．
14.数学课上，老师提出如下问题：△ABC是⊙O的内接三角形，OD⊥BC于点D.请借助直尺，画出△ABC中∠BAC的平分线.
晓龙同学的画图步骤如下：
①延长OD交 于点M；
②连接AM交BC于点N.
所以线段AN为所求△ABC中∠BAC的平分线.
请回答：晓龙同学画图的依据是________.
15.刘徽是我国魏晋时期卓越的数学家，他在《九章算术》中提出了“割圆术”，利用圆的内接正多边形逐步逼近圆来近似计算圆的面积，如图，若用圆的内接正十二边形的面积 来近似估计 的面积 ，设 的半径为1，则 ________. 21cnjy.com
16.如图，水平地面有一个面积为120πcm2的灰色扇形OAB，其中OA的长度为12cm，且OA与地面垂直．若在没有滑动的情况下，将图最左边的扇形向右滚动至点A 再一次接触地面时，则O点移动的路径长为________．
三、解答题
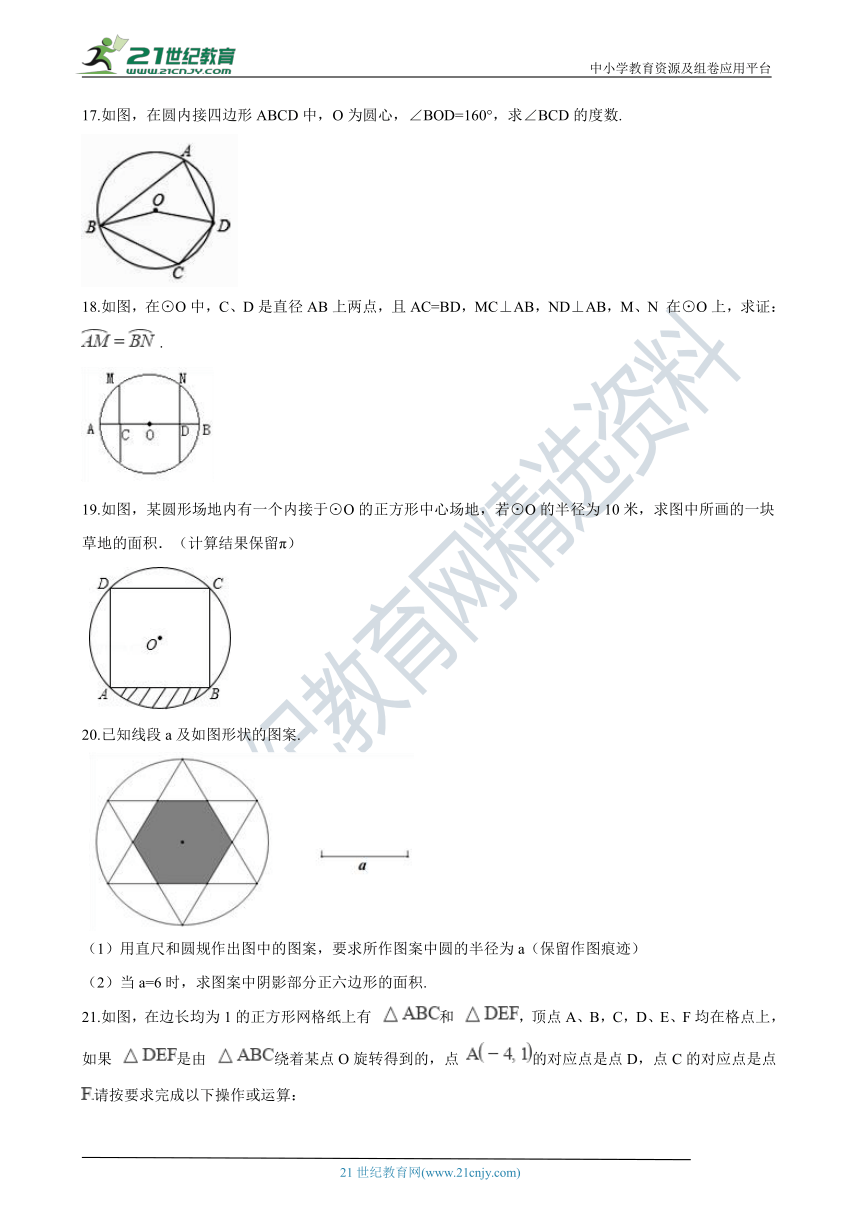
17.如图，在圆内接四边形ABCD中，O为圆心，∠BOD=160°，求∠BCD的度数.
18.如图，在⊙O中，C、D是直径AB上两点，且AC=BD，MC⊥AB，ND⊥AB，M、N在⊙O上，求证： ?.
19.如图，某圆形场地内有一个内接于⊙O的正方形中心场地，若⊙O的半径为10米，求图中所画的一块草地的面积．（计算结果保留π）

20.已知线段a及如图形状的图案.

（1）用直尺和圆规作出图中的图案，要求所作图案中圆的半径为a（保留作图痕迹）
（2）当a=6时，求图案中阴影部分正六边形的面积.
21.如图，在边长均为1的正方形网格纸上有 和 ，顶点A、B，C，D、E、F均在格点上，如果 是由 绕着某点O旋转得到的，点 的对应点是点D，点C的对应点是点 请按要求完成以下操作或运算：
（1）在图上找到点O的位置 不写作法，但要标出字母 ，并写出点O的坐标；
（2）求点B绕着点O顺时针旋转到点E所经过的路径长.
22.如图，四边形ABCD为圆内接四边形，对角线AC、BD交于点E，延长DA、CB交于点F，且∠CAD＝60°，DC＝DE．

求证：
（1）AB＝AF；
（2）A为△BEF的外心（即△BEF外接圆的圆心）．
23.如图，BD为△ABC外接圆⊙O的直径，且∠BAE=∠C．
（1）求证:AE与⊙O相切于点A；
（2）若AE∥BC，BC=2 ，AC=2 ，求AD的长．
24.问题呈现：阿基米德折弦定理：如图1，AB和BC是⊙O的两条弦（即折线ABC是圆的一条折弦），BC＞AB，M是 的中点，则从M向BC所作垂线的垂足D是折弦ABC的中点，即CD＝AB+BD．下面是运用“截长法”证明CD＝AB+BD的部分证明过程．
证明：如图2，在CB上截取CG＝AB，连接MA，MB，MC和MG
∵M是 的中点，
∴MA＝MC
……
（1）请按照上面的证明思路，写出该证明的剩余部分；
（2）实践应用：
①如图3，已知△ABC内接于⊙O，BC＞AB＞AC，D是 的中点，依据阿基米德折弦定理可得图中某三条线段的等量关系为________；
②如图4，已知等腰△ABC内接于⊙O，AB＝AC，D为 上一点，连接DB，∠ACD＝45°，AE⊥CD于点E，△BCD的周长为4 +2，BC＝2，请求出AC的长．________
答案解析部分
一、单选题
1. C
解析：①旋转120°后，图形可以与原来的位置重合，故正确；
②旋转120°后，图形可以与原来的位置重合，故正确；
③五角星中心角是72°，120不是72的倍数，图形无法与原来的位置重合，故错误；
④旋转90°后，图形无法与原来的位置重合，故错误．
故答案为：C．
【分析】由三角形、五边形、正方形的内角和定理分别求出各内角的度数，再结合旋转的性质即可判断求解。
2. C
解析：连接AC，
∵AB＝3cm，AD＝4cm，
∴AC＝5cm，
∵AB＝3＜4，AD＝4＝4，AC＝5＞4，
∴点B在⊙A内，点D在⊙A上，点C在⊙A外．
故答案为：C．
【分析】连接AC，根据勾股定理求出AC的长，要想判断点B、C、D与?⊙A 的位置关系，就是将AB、AC、AD的长分别与半径4比较即可.
3. B
解析：A、同一平面上三点必须不在同一直线上才可以确定一个圆，故本选项不符合题意；
B、能够重合的弧是等弧，符合题意；
C、三角形的外心到三角形三个顶点的距离相等，到三边的距离不一定相等，故本选项不符合题意；
D、菱形的对角相等，但不一定互补，所以四个顶点不一定在同一个圆上，故本选项不符合题意．
故答案为：B． 【分析】A.不共线三点才能确定一个圆 C.外心到三角形三个顶点的距离相等。
4. B
解析： 将正方形ABCD绕A按逆时针方向旋转180°至正方形AB1C1D1 ∴CC1=2AC=2×AB= ∴线段CD扫过的面积为 故答案为：B 【分析】根据旋转的轨迹，可利用圆的面积公式求得结果。
5. A
解析：∵ 如图1， 弦AB，BC的垂直平分线，交点O， ∴OA=OB=OC ∴点O就是过点A、B、C三点的圆的圆心，故①能确定圆心O； ∵ 如图2，在圆上任取一点B，以B为圆心，小于直径长为半径画弧交圆于A，C两点， ∴AB=CB ∵∠ABC的角平分线交圆O于点D ∴BD垂直平分AC ∴BD是直径， ∵ 弦BD的垂直平分线交BD于点O ∴点O是圆心，故②能确定圆心； ∵ 如图3，在圆上截取弦AB=CD，连结AB，BC，CD，分别作∠ABC与∠DCB的平分线， 两角平分线的交点O不能证明是圆心，故③不能确定点O是圆心； 故答案为：A. 【分析】利用线段垂直平分线的性质，易证OA=OB=OC，根据三角形外接圆的定义证得点O是圆心，可对①作出判断；由作图可知AB=CD，再由∠ABC的角平分线交圆O于点D，利用等腰三角形三线合一的性质，可证得BD垂直平分AC，利用垂径定理可知BD是直径，然后根据 弦BD的垂直平分线交BD于点O ，可确定点O时是圆心，可对②作出判断；根据图3的作图不能证明点O是圆心，可对③作出判断，综上所述可得出结论。
6. A
解析：∵OA=OB，∴∠B=∠A=50°，∠AOB=80°， 又∵C是 的中点 ， ∴∠BOC=∠AOC=40°。 故答案为：A。 【分析】由OA=OB，可求得∠AOB的大小，由 C是 的中点可得出弧AC等于弧BC，故∠BOC=∠AOC=40°。
7. C
解析：设圆心为 ，连接 ，如图，
∵弦 的长度等于圆半径的 倍，
即 ，
∴ ，
∴ 为等腰直角三角形， ，
∴ 。
故答案为：C。
【分析】设圆心为 ，连接 ，如图，根据勾股定理的逆定理判断出 为等腰直角三角形， ，然后根据同弧所对的圆周角等于圆心角的一半即可得出答案。
8. D
解析：∵ ， ∴∠A=72°, ∵ 四边形ABCD是 的内接四边形 , ∴∠C=180°－∠A=180°－72°=108°. 故答案为：D。 【分析】根据同弧所对的圆周角等于圆心角的一半得出∠A=72°,根据圆内接四边形的对角互补即可算出∠C的度数。
9. A
解析：∵圆内接正六边形的周长为24，
∴圆内接正六边形的边长为4，
∴圆的半径为4，
如图，
连接OB，过O作OD⊥BC于D，
则∠OBC=30°，BD=OB?cos30°=4× =2 ，
∴BC=2BD=4 ；
∴该圆的内接正三角形的周长为12 ，
故答案为：A．
【分析】由正六边形的周长求出正六边形的边长，再根据正六边形的边长和半径相等，可得出半径的长，连接OB，过O作OD⊥BC于D，利用解直角三角形求出BD的长，利用垂径定理，就可求出该圆的内接正三角形的边长，从而可求出此三角形的周长。2-1-c-n-j-y
10. A
解析：连接OA、OB，
∵正方形ABCD内接于⊙O，
∴AB=BC=DC=AD，
∴ ，
∴∠AOB= ×360°=90°，
在Rt△AOB中，由勾股定理得：2AO2=（2 ）2 ，
解得：AO=2，
∴ 的长为 =π，
故答案为：A． 【分析】连接OA、OB，根据同圆中弧，弦，圆心角之间的关系可知∠AOB=90°，利用勾股定理求出半径OA，再代入弧长的计算公式即可求出 的长.【来源：21·世纪·教育·网】
二、填空题
11. 6
解析：∵正n边形的一个内角为120°，
∴它的外角为180°-120°=60°，
360°÷60°=6，
故答案为：6． 【分析】先求出正n边形的外角，利用多边形的外角和与外角即可求出n.
12.(6，2)
解析：圆心是BC，AB两边垂直平分线的交点为(6，2)．
【分析】由网格图像的特点和三角形的外心是三角形三条垂直平分线的交点可求解。
13.
解析：过圆心点O作OE⊥AB于点E，连接OC，
∵点C是该门的最高点，
∴ ，
∴CO⊥AB，
∴C，O，E三点共线，
连接OA，
∵OE⊥AB，
∴AE= =0.5m，
设圆O的半径为R，则OE=2.5-R，
∵OA2=AE2+OE2 ，
∴R2=（0.5）2+（2.5-R）2 ，
解得：R= ，
故答案为： ．
【分析】过圆心点O作OE⊥AB于点E，连接OC，根据圆的对称性得出 ，根据垂径定理得出CO⊥AB，故C，O，E三点共线，AE= =0.5m，连接OA，根据勾股定理建立方程，求解即可。
14. 垂径定理和在同圆或等圆中，同弧或等弧所对的圆周角相等.
解析：如图所示：线段AN为所求△ABC中∠BAC的平分线，
画图的依据是垂径定理和在同圆或等圆中，同弧或等弧所对的圆周角相等；
故答案为：垂径定理和在同圆或等圆中，同弧或等弧所对的圆周角相等.
【分析】根据垂径定理得出弧BM=弧CM，再根据等弧所对的圆周角相等得出∠BAN=∠CAN，故线段AN为所求△ABC中∠BAC的平分线。21·cn·jy·com
15.
解析：如图，过点A作AC⊥OB，垂足为C，
∵ 的半径为1，
∴ 的面积 ，OA=OB=1，
∴圆的内接正十二边形的中心角为∠AOB= ，
∴AC= OB= ，
∴S△AOB= OB?AC= ，
∴圆的内接正十二边形的面积S1=12S△AOB=3，
∴则 ，
故答案为： .
【分析】过点A作AC⊥OB，垂足为C，圆的半径为1，就可求出圆O的面积，再利用正多边形的性质，求出中心角∠AOB的度数，利用直角三角形的性质求出AC的长，就可求出△AOB的面积，再根据S1=12S△AOB，求出S1，然后求出S-S1的值即可。21世纪教育网版权所有
16. 22π
解析：设扇形的圆心角为n，则 ＝120π
∴n＝300°
∵扇形的弧长为 ＝20π
∴点O从开始到移动到OB与直线垂直，移动的距离20πcm．
∵∠AOB＝360﹣300＝60°，
则△AOB是等边三角形，
∴AB＝OA＝12cm，
则在最后一个图形的位置旋转到A与直线接触，O移动的距离是： ＝2π，
则O点移动了22π．
故答案为：22π． 【分析】设扇形的圆心角为n，根据扇形面积公式，由扇形的面积建立方程，求解得出灰色扇形的圆心角，然后根据扇形的弧长计算公式算出灰色扇形的弧长，图形从第一个位置，在没有滚动的情况下运动到最后一个位置， O点移动的路径长 就会说灰色扇形的弧长；然后判断出△AOB是等边三角形，则在最后一个图形的位置旋转到A与直线接触，O移动的距离应该是以B为旋转中心，OB为半径，旋转角是30°的一段弧长，根据弧长计算公式算出再与第一次移动的距离即可。21·世纪*教育网
三、解答题
17. 解：∵∠BOD=160°∴∠BAD=
∵A、B、C、D四点共圆，
∴∠BCD+∠BAD=180°，
∴∠BCD=100°.
【分析】由圆周角定理得∠BAD=∠BOD，再根据圆内接四边形的对角互补可求得∠BCD的度数。【来源：
18.解：连结OM、ON，如图， ∵AB是⊙O的直径，C、D是直径AB上两点，且AC＝BD，∴OC=OD，∵CM⊥AB，DN⊥AB，∴∠OCM=∠ODN=90°，在Rt△OMC和Rt△OND中 ?，∴Rt△OMC≌Rt△OND（HL），∴∠COM=∠DON，∴ 21*cnjy*com
【分析】连结OM、ON，由题意用斜边直角边定理易证Rt△OMC≌Rt△OND，所以可得对应角∠COM=∠DON，根据在同圆或等圆中，如果圆心角、弦、弧三组量中，有其中一组量相等，那么其余各组量也分别相等可得弧AM=弧BN。www.21-cn-jy.com
19. 解：连AC，则AC为直径，即AC=20，

∵正方形ABCD中，
AB=BC，∠B=90°，
∴在Rt△ABC中，
AB2+BC2=AC2 ，
2AB2=202 ，
∴AB2=200，
= =（25π﹣50）米2 ．
【分析】连AC，易证AC是圆的直径，利用勾股定理，在Rt△ABC中，求出AB2 ， 再由， 计算可求解。
20. （1）解：所作图形如下图所示：
（2）解：如下图，

连接OA、OB、OC、OD，作OE⊥AB于点E，则由题意可得：OA=OB=6，∠AOB=120°，∠OEB=90°，AE=BE，△BOC，△AOD都是等腰三角形，△OCD的三边三角形，【版权所有：21教育】
∴∠ABO=30°，BC=OC=CD=AD，
∴BE=OB·cos30°= ，OE=3，
∴AB= ，
∴CD= ，
∴S△OCD= ，
∴S阴影=6S△OCD= .
【分析】（1）由正六边形的性质可知，圆的半径等于正六边形的边长，而正六边形将圆分成相等的六部分，所以只需作出以线段a为半径的圆，再以线段a的长为半径顺次在圆周上截取6部分即可求解； （2） 连接OA、OB、OC、OD，作OE⊥AB于点E?。由正六边形和等边三角形的性质即可求解。
21. （1）解：如图所示，连接AD，CF，作AD和CF的垂直平分线，交于点O，则点O即为旋转中心，由点A（﹣4，1）可得直角坐标系，故点O的坐标为（1，﹣1）；
（2）解：点B绕着点O顺时针旋转到点E所经过的路径长为：
【分析】（1）根据旋转的性质：每一对对应点到旋转中心的距离相等，故连接AD，CF，作AD和CF的垂直平分线，其交点O即为旋转中心 ；根据点A的坐标特点，过点A向右数4个单位长度后的点作竖直线，再过点A向下数一个单位长度后的点作水平线，两线的交点为坐标原点，建立平面直角坐标系，利用方格纸的特点即可读出点O的坐标； （2）利用方格纸的特点即可发现： 点B绕着点O顺时针旋转到点E所经过的路径长就是半径为3，旋转角是90°的一段弧长，根据弧长计算公式即可算出答案。www-2-1-cnjy-com
22. （1）证明：∠ABF＝∠ADC＝120°﹣∠ACD＝120°﹣∠DEC
＝120°﹣（60°+∠ADE）＝60°﹣∠ADE，
而∠F＝60°﹣∠ACF，
因为∠ACF＝∠ADE，
所以∠ABF＝∠F，所以AB＝AF． （2）证明：四边形ABCD内接于圆，所以∠ABD＝∠ACD，
又DE＝DC，所以∠DCE＝∠DEC＝∠AEB，
所以∠ABD＝∠AEB，
所以AB＝AE．
∵AB＝AF，
∴AB＝AF＝AE，即A是三角形BEF的外心．
【分析】（1）根据圆的内接四边形的一个外角等于它的内对角得出 ∠ABF＝∠ADC，根据三角形的内角和得出 ∠ADC＝120°﹣∠ACD，根据等边对等角得出 ∠ADC＝ 120°﹣∠DEC，根据三角形的一个外角等于与它不相邻的两个内角的和得出 ∠DEC= 60°+∠ADE，故 ∠ABF= 60°﹣∠ADE， 根据三角形的一个外角等于与它不相邻的两个内角的和得出 ∠F＝60°﹣∠ACF，根据同弧所对的圆周角相等得出 ∠ACF＝∠ADE， 所以∠ABF＝∠F，根据等角对等边得出AB＝AF； （2）根据同弧所对的圆周角相等得出 ∠ABD＝∠ACD，根据等边对等角及对顶角相等得出 ∠DCE＝∠DEC＝∠AEB，故 ∠ABD＝∠AEB，根据等角对等边得出 AB＝AE，又 AB＝AF，故 AB＝AF＝AE，即A是三角形BEF的外心．
23. （1）证明:如图，连接OA，交BC于F，
则OA=OB，
∴∠D=∠DAO，
∵∠D=∠C，
∴∠C=∠DAO，
∵∠BAE=∠C，
∴∠BAE=∠DAO，
∵BD是⊙O的直径，
∴∠BAD=90°，
即∠DAO+∠BAO=90°，
∴∠BAE+∠BAO=90°，即∠OAE=90°，
∴AE⊥OA，
∴AE与⊙O相切于点A（2）解:∵AE∥BC，AE⊥OA，
∴OA⊥BC，
∴ ，FB= BC，
∴AB=AC，
∵BC=2 ，AC=2 ，
∴BF= ，AB=2 ，
在Rt△ABF中，AF= =1，
在Rt△OFB中，OB2=BF2+（OB﹣AF）2 ，
∴OB=4，
∴BD=8，
∴在Rt△ABD中，AD= ．
【分析】（１）连接OA，交BC于F，易知 ∠D=∠DAO，根据同弧所对的圆周角相等可知∠D=∠C，又 ∠BAE=∠C， 即得 ∠BAE=∠DAO，由直径所对的圆周角是直角，可知 ∠BAD=90° ，易证 ∠OAE=90°，?便得到 AE与⊙O相切于点； （２）根据条件可知OA⊥BC，?根据垂径定理可知弧AB＝弧AC，FB=?BC，?易得到AB=AC，利用勾股定理求出AF、OB的长，再利用勾股定理即可求出AD的长。
24. （1）证明：如图2，在CB上截取CG＝AB，连接MA，MB，MC和MG．
∵M是 的中点，
∴MA＝MC．
在△MBA和△MGC中 ，
∴△MBA≌△MGC（SAS），
∴MB＝MG，
又∵MD⊥BC，
∴BD＝GD，
∴DC＝GC+GD＝AB+BD（2）BE＝CE+AC；根据阿基米德折弦定理得，CE＝BD+DE，
∵△BCD的周长为4 +2，
∴BD+CD+BC＝4 +2，
∴BD+DE+CE+BC＝2CE+BC＝4 +2，
∵BC＝2，
∴CE＝2 ，
在Rt△ACE中，∠ACD＝45°，
∴AC＝ CE＝4．
解析：（2）①解：根据阿基米德折弦定理得，BE＝CE+AC，
答案为：BE＝CE+AC；
【分析】（1）在CB上截取CG＝AB，连接MA，MB，MC和MG，圆周角定理可证得MA=MC，再利用SAS证明△MBA≌△MGC，利用全等三角形的性质可知MB=MG，利用等腰三角形三线合一的性质，可证得BD=CG，继而可证得结论。 （2）①由阿基米德折弦定理可得出BE、DE、CE之间的数量的关系；② 根据阿基米德折弦定理得，CE＝BD+DE，再由已知△BCD的周长和BC的长，就可证得BD+CD+BC=2CE+BC=， 从而可求出CE的长，在等腰Rt△ACE中，利用解直角三角形求出AC即可。21*cnjy*com