2019-2020浙教版九年级数学上册第三章圆的基本性质单元培优试卷(解析版)
文档属性
| 名称 | 2019-2020浙教版九年级数学上册第三章圆的基本性质单元培优试卷(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 292.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-26 00:00:00 | ||
图片预览


文档简介
2019-2020浙教版九年级数学上册第三章圆的基本性质单元培优试卷
一、选择题(每小题3分,共30分)
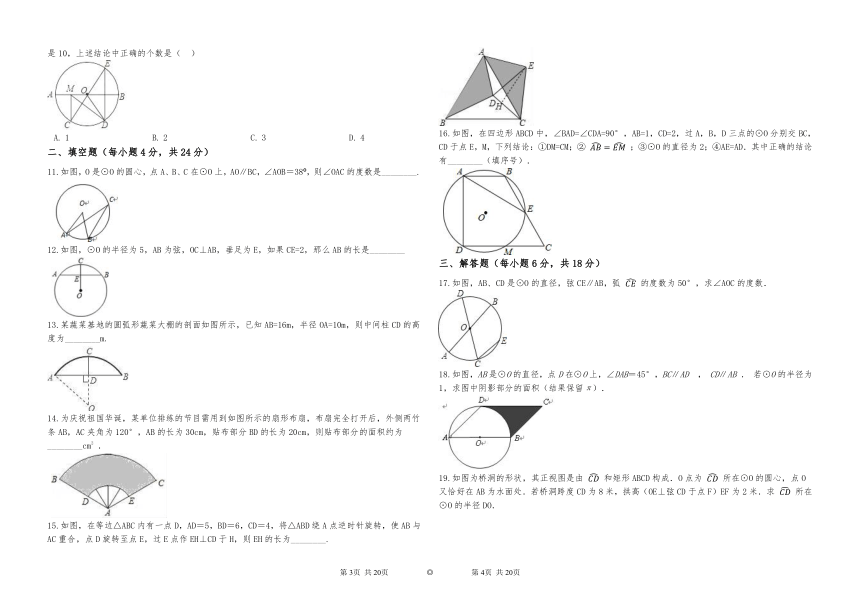
1.△ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是( )
A.80° B.160° C.100° D.80°或100°
2.如图,将△OAB绕点O逆时针旋转80°,得到△OCD.若∠A=2∠D=100°,则∠α的度数是(?? )
A.?50°??????????????????????????????B.?60°??????????????????????????????C.?40°??????????????????????????????D.?30°
3.如图,平面直角坐标系中,已知点B ,若将△ABO绕点O沿顺时针方向旋转90°后得到△A1B1O,则点B的对应点B1的坐标是(???? )
A.?(3,1)??????????????????B.?(3,2)??????????????????C.?(1,3)??????????????????D.?(2,3)
4.如图,四边形 是⊙ 的内接正方形,点 是劣弧 上任意一点(与点 不重合),则 的度数为(?? )
A.?30°???????????????????????????B.?45°???????????????????????????C.?60°???????????????????????????D.?无法确定
5.已知圆的半径为3,扇形的圆心角为 ,则扇形的面积为 (?? )
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
6.如图,在正方形ABCD中,分别取AD、BC的中点E、F,并连接EF;以点F为圆心,FD的长为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则 的值为(?? )
A.? ?? ???C. ?? D.
7.如图,AB是⊙O的弦,AB=5,点C是⊙O上的一个动点,且∠ACB=45°,点M,N分别是AB,AC的中点,则线段MN长的最大值为( ??)
A.?5???????????????????????????B.?????????????????????????????C.?5 ???????????????????????????D.?
8.如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB’C’D’ , 图中阴影部分的面积为(?? ).
A.???????????????????????????B.???????????????????????C.???????????????????????D.?
9.如图,已知圆O的半径为10,AB⊥CD,垂足为P,且AB=CD=16,则OP的长为(?? )
A.?6?????????????????????????????B.?6 ??????????????????????????????C.?8??????????????????????????????D.?8
10.如图,在⊙O中,AB是⊙O的直径,AB=10, = = ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED= ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是(?? )
A.?1??????????????????????????????????B.?2??????????????????????????????????C.?3??????????????????????????????????D.?4
二、填空题(每小题4分,共24分)
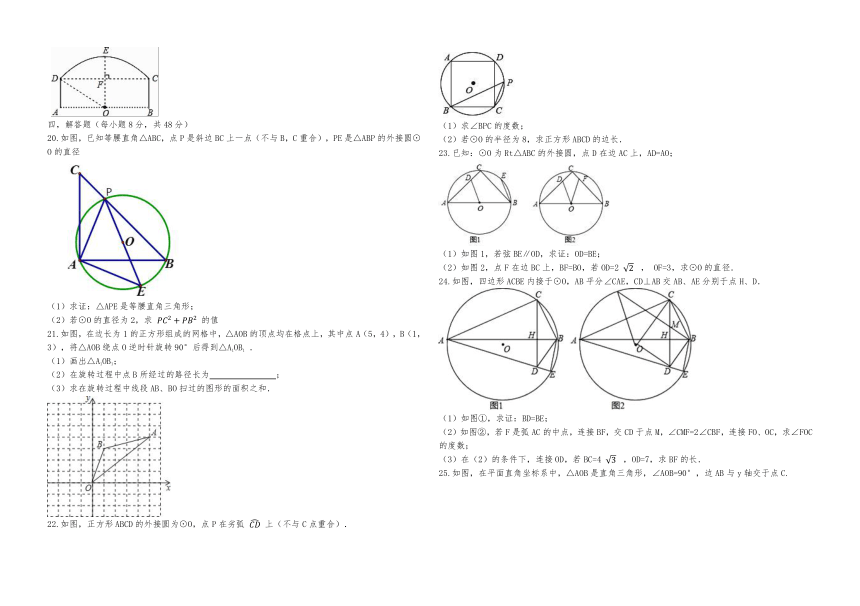
11.如图,O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=38?,则∠OAC的度数是________.
12.如图,⊙O的半径为5,AB为弦,OC⊥AB,垂足为E,如果CE=2,那么AB的长是________
13.某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为________m.
14.为庆祝祖国华诞,某单位排练的节目需用到如图所示的扇形布扇,布扇完全打开后,外侧两竹条AB,AC夹角为120°,AB的长为30cm,贴布部分BD的长为20cm,则贴布部分的面积约为________cm2 .
15.如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,过E点作EH⊥CD于H,则EH的长为________.
16.如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,下列结论:①DM=CM;② ;③⊙O的直径为2;④AE=AD.其中正确的结论有________(填序号).
三、解答题(每小题6分,共18分)
17.如图,AB、CD是⊙O的直径,弦CE∥AB,弧 的度数为50°,求∠AOC的度数.
18.如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD , CD∥AB . 若⊙O的半径为1,求图中阴影部分的面积(结果保留π).
19.如图为桥洞的形状,其正视图是由 和矩形ABCD构成.O点为 所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F)EF为2米.求 所在⊙O的半径DO.
四,解答题(每小题8分,共48分)
20.如图,已知等腰直角△ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求 的值
21.如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1 .
(1)画出△A1OB1;
(2)在旋转过程中点B所经过的路径长为?? ? ? ? ? ? ? ? ? ?;
(3)求在旋转过程中线段AB、BO扫过的图形的面积之和.
22.如图,正方形ABCD的外接圆为⊙O,点P在劣弧 上(不与C点重合).
(1)求∠BPC的度数;
(2)若⊙O的半径为8,求正方形ABCD的边长.
23.已知:⊙O为Rt△ABC的外接圆,点D在边AC上,AD=AO;
(1)如图1,若弦BE∥OD,求证:OD=BE;
(2)如图2,点F在边BC上,BF=BO,若OD=2 ?, OF=3,求⊙O的直径.
24.如图,四边形ACBE内接于⊙O,AB平分∠CAE,CD⊥AB交AB、AE分别于点H、D.
(1)如图①,求证:BD=BE;
(2)如图②,若F是弧AC的中点,连接BF,交CD于点M,∠CMF=2∠CBF,连接FO、OC,求∠FOC的度数;
(3)在(2)的条件下,连接OD,若BC=4 ?,OD=7,求BF的长.
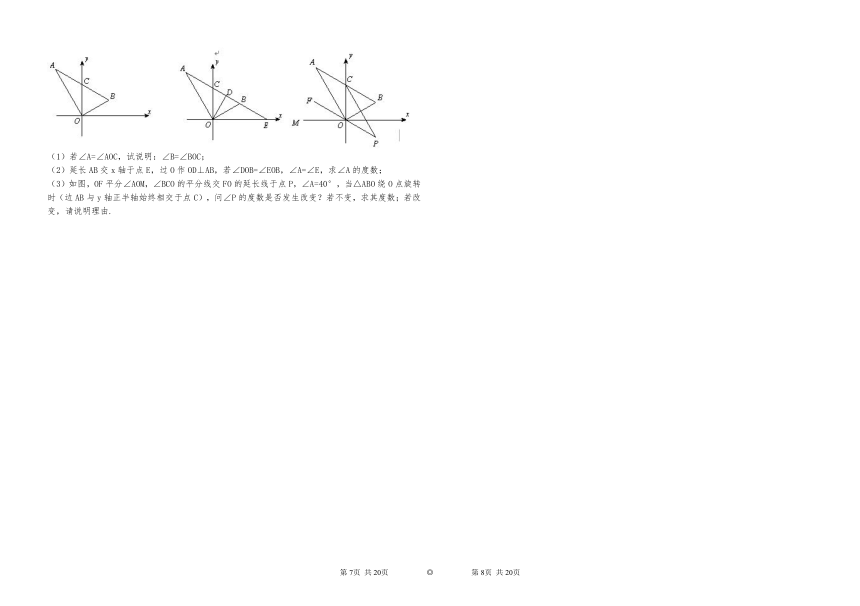
25.如图,在平面直角坐标系中,△AOB是直角三角形,∠AOB=90°,边AB与y轴交于点C.
(1)若∠A=∠AOC,试说明:∠B=∠BOC;
(2)延长AB交x轴于点E,过O作OD⊥AB,若∠DOB=∠EOB,∠A=∠E,求∠A的度数;
(3)如图,OF平分∠AOM,∠BCO的平分线交FO的延长线于点P,∠A=40°,当△ABO绕O点旋转时(边AB与y轴正半轴始终相交于点C),问∠P的度数是否发生改变?若不变,求其度数;若改变,请说明理由.
答案
一、选择题(每小题3分,共30分)
1. 解:∠ABC=∠AOC=×160°=80°或∠ABC=×(360°-160°)=100°.
故答案为:D.
2.解:根据旋转的意义,图片按逆时针方向旋转80°,可得∠AOC=80°,∠C=∠A,
∵∠A=2∠D=100°
∴∠A=100°,∠D=50°,
∴∠DOC=180°-∠C-∠D=30°,
∴∠a=∠AOC-∠DOC=50°
故答案为:A.
3.解:△A1B1O如图所示,点B1的坐标是(2,3).
故答案为:D.
4.解:连接OB,OC,
∵ 四边形 是⊙ 的内接正方形 ,
∴∠BOC==90°,
∴∠BPC=∠BOC=45°;
故答案为:? B.
5.解: 扇形的圆心角为 ,其半径为3,
。
故答案为:C。
6.
解:设正方形的边长为2,则CD=AB=2,CF=1
在直角三角形DCF中,DF== ,∴FG=EH= ,∴DH= -1
∴ = ,
故答案为:A.
7.解:∵ 点M,N分别是AB,AC的中点,
∴MN=BC,
∴当BC最大时,线段MN的长最大,
∴当BC为 ⊙O 直径时,BC长度最大,
∴∠BA=90°,
在Rt△BAC中,
∵ ∠ACB=45°, AB=5,
∴AC=5,BC==5
∴MN=BC= ,
即线段MN的长的最大值为.
故答案为:D.
8. 解:如图,设B′C′与CD的交点为E , 连接AE ,
在Rt△AB′E和Rt△ADE中,
,
∴Rt△AB′E≌Rt△ADE(HL),
∴∠DAE=∠B′AE ,
∵旋转角为30°,
∴∠DAB′=60°,
∴∠DAE= ×60°=30°,
∴DE=1× = ,
∴阴影部分的面积=1×1﹣2×( ×1× )=1﹣ .
故答案为:C .
9.解:作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,
∵AB=CD=16,
∴BM=DN=8,
∴OM=ON= =6,
∵AB⊥CD,
∴∠DPB=90°,
∵OM⊥AB于M,ON⊥CD于N,
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形,
∵OM=ON,
∴四边形MONP是正方形,
∴OP= .
故答案为:B.
10.解:∵ = = , 点E是点D关于AB的对称点,
∴ = ,
∴∠DOB=∠BOE=∠COD= =60°,∴①正确;
∠CED= ∠COD= =30°= ,∴②正确;
∵ 的度数是60°,
∴ 的度数是120°,
∴只有当M和A重合时,∠MDE=60°,
∵∠CED=30°,
∴只有M和A重合时,DM⊥CE,∴③错误;
做C关于AB的对称点F,连接CF,交AB于N,连接DF交AB于M,此时CM+DM的值最短,等于DF长,
连接CD,
∵ = = = ,并且弧的度数都是60°,
∴∠D= =60°,∠CFD= =30°,
∴∠FCD=180°﹣60°﹣30°=90°,
∴DF是⊙O的直径,
即DF=AB=10,
∴CM+DM的最小值是10,∴④正确;
答案为:C.
二、填空题(每小题4分,共24分)
11.解:∵∠AOB=38?,
∴∠ACB=19°,
又∵AO∥BC,
∴∠OAC=∠ACB=19°.
故答案为:19°.
12.解:如图,连接OA;
∵OC=5,CE=2,
∴OE=OC-CE=3,
∵ OC⊥AB ,
∴AB=2AE,
在Rt△AOE中,由勾股定理得:AE2+OE2=AO2 ,
又OA=5,OE=3,
∴AE=4,
∴AB=2AE=8;
故答案为8.
13.解:∵CD垂直平分AB,
∴AD=8.
∴OD= =6m,
∴CD=OC-OD=10-6=4(m).
14.解:贴布部分的面积=S扇形BAC-S扇形DAE
= -
= (cm2).
故答案为 .
15.解:∵△ABC为等边三角形,
∴∠BAC=60°,AB=AC,
∵将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,
∴∠DAE=∠BAC=60°,AD=AE=5,CE=BD=6,
∴△ADE为等边三角形,
∴DE=AD=5,
设DH=x,则CH=CD﹣DH=4﹣x,
在Rt△DHE中,EH2+x2=52 , ①
在Rt△CHE中,EH2+(4﹣x)2=62 , ②
②﹣①得16﹣8x=11,解得x= ,
∴EH= = .
故答案为 .
16.解:如下图,连接AM,连接MB,过点O作OG⊥AM,OH⊥AM,
∵∠BAD=∠CDA=90°,
∴AM过圆心O,而A、D、M、B四点共圆,
∴四边形ADMB为矩形,
∵AB=1,CD=2,
∴CM=2-1=1=AB=DM,
故①正确;
又∵AB∥CD,
∴四边形ABMC为平行四边形,
∴∠AEB=∠MAE, = ,
故②正确;
∵四边形ADMB为矩形,
∴AB=DM,
∴ = ,
∴= ,
∴∠DAM=∠EAM,
过点O作OG⊥AM,OH⊥AM,
∴OG=OH,
∴AD=AE,
故④正确;
由题设条件求不出直径的大小,
故③⊙O的直径为2,错误;
故答案为:①②④.
三、解答题(每小题6分,共18分)
17.解:连接OE,如图,
∵ 的度数为50°,
∴∠COE=50°,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OCE=(180°﹣50°)÷2=65°,
∵CE∥AB,
∴∠AOC=∠OCE=65°.
18.解:∵BC∥AD,CD∥AB,
∴四边形ABCD是平行四边形,
∴CD=AB=2,
∴S梯形OBCD==;
∴图中阴影部分的面积=S梯形OBCD-S扇形OBD=-×π×12=-。
四、解答题(每小题8分,共48分)
19. 解:∵OE⊥弦CD于点F,CD为8米,EF为2米,
∴EO垂直平分CD,DF=4m,FO=DO﹣2,
在Rt△DFO中,DO2=FO2+DF2 , 则DO2=(DO﹣2)2+42 , 解得:DO=5.
答:弧CD所在⊙O的半径DO为5m
20.(1)证明:∵△ABC是等腰直角三角形,
∴∠C=∠ABC=45°,
∴∠PEA=∠ABC=45°
又∵PE是⊙O的直径,
∴∠PAE=90°,
∴∠PEA=∠APE=45°,
∴ △APE是等腰直角三角形.
(2)解:∵△ABC是等腰直角三角形,
∴AC=AB,
同理AP=AE,
又∵∠CAB=∠PAE=90°,
∴∠CAP=∠BAE,
∴△CPA≌△BAE,
∴CP=BE,
在Rt△BPE中,∠PBE=90°,PE=2,
∴PB2+BE2=PE2,
∴CP2+PB2=PE2=4.
21.解:(1)△A1OB1如图所示;
(2)由勾股定理得,BO==,
所以,点B所经过的路径长==π;
故答案为:π.
(3)由勾股定理得,OA==,
∵AB所扫过的面积=S扇形A1OA+S△A1B1O﹣S扇形B1OB﹣S△AOB=S扇形A1OA﹣S扇形B1OB ,
BO扫过的面积=S扇形B1OB ,
∴线段AB、BO扫过的图形的面积之和=S扇形A1OA﹣S扇形B1OB+S扇形B1OB ,
=S扇形A1OA ,
=,
=π.
?
22. (1)解:连接OB,OC,∵四边形ABCD为正方形,∴∠BOC=90°,∴∠BPC= ∠BOC=45°;
(2)解:过点O作OE⊥BC于点E, ∵OB=OC,∠BOC=90°,∴∠OBE=45°,∴OE=BE,∵OE2+BE2=OB2 , ∴BE= ?∴BC=2BE=2×
23.(1)证明:连接AE交OD于点F.
∵AB为直径,
∴AE⊥BE,
∵BE∥OD,
∴AE⊥OD,
∵AD=AO,
∴AE平分∠CAB,
∴OD=2OF,
∵BE=2OF,
∴BE=OD;
(2)解:分别作弦BE∥OD,AH∥OF,连接AE,BH,AE与BH交于点P,
由(1)得:E为弧BC的中点,同理H为弧AC的中点,
∴∠HAE=∠HBE=45°,
∵AB为直径,
∴∠H=∠E=90°,
∴AP= AH,PE=BE,
∵点O为AB的中点,BE∥OD,
∴EB=OD= ,
∴PE=BE= ,同理AH=OF=3,
∴AP= ,在Rt△ABE中,AE= ,BE= ,
根据勾股定理得:AB= ,
则圆的直径为 .
24. (1)解:如图1,连接OB、OC、OE,
∵AB平分∠CAE,
∴∠CAB=∠BAE,
∴∠COB=∠BOE,
∴BC=BE,
∵CD⊥AB,
∴∠CHA=∠DHA=90°,
∵∠CAB=∠BAE,AH=AH,
∴△ACH≌△ADH,
∴CH=DH,
∴AB为线段CD的垂直平分线,
∴BC=BD,
∴BD=BE;
(2)解:∵F是弧AC的中点,
∴ ?,
∴∠CBF=∠ABF,
∵∠CMF=2∠CBF,
∴∠CMF=2∠ABF,
∵CD⊥AB,∠CMF=∠BMH,
∴∠BMH+∠ABF=90°,
∴∠ABF=30°,
∴∠CBF=30°,
∵∠FOC=2∠CBF,
∴∠FOC=60°
(3)解:如图3,连接OM,OB,作ON⊥BF于N,DK⊥OM于K,
由(2)可知:∠CBF=∠ABF=∠BCH=30°,
∴CM=BM,
在Rt△CBH中,∠BCH=30°,BC=4 ,
∴BH=2 ,CH=6,
在Rt△BHM中,∠MBH=30°,BH=2 ,
∴BM=4? HM=2,
∴CM=BM=4,
∵OC=OB,OM=OM,
∴△OMC≌△OMB,
∴∠CMO=∠BMO=120°,∠OMF=∠OMD=60°,
∵CH=DH=6,
∴DM=8,
在Rt△DMK中,∠KMD=60°,DM=8,
∴MK=4,DK=4 ,
在Rt△OKD中,
OD2=OK2+DK2 ,
∵OD=7,DK=4 ,
∴OK=1,
∴OM=5,
在Rt△OMN中,∠OMN=60°,OM=5,
MN= OM= ,
∴BN=BM+MN= ,
∵ON⊥BF,
∴BF=2BN=13.
25. (1)解:∵△AOB是直角三角形??
∴∠A+∠B=90°,∠AOC+∠BOC=90°???
∵∠A=∠AOC???? ∴∠B=∠BOC
(2)解:∵∠A+∠ABO=90°,∠DOB+∠ABO=90°
∴∠A=∠DOB??????? 即∠DOB=∠EOB=∠OAE=∠OEA
∵∠DOB+∠EOB+∠OEA=90°?????? ∴∠A=30°
(3)解:∠P的度数不变,∠P=25°.
∵∠AOM=90°-∠AOC,∠BCO=∠A+∠AOC
又OF平分∠AOM,CP平分∠BCO
∴∠FOM=45°- ∠AOC,∠PCO= ∠A+ ∠AOC
∴∠P=180°-(∠PCO+∠FOM+90°)=45°- ∠A=25°
的度数.
第3页 共4页 ◎ 第4页 共4页
一、选择题(每小题3分,共30分)
1.△ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是( )
A.80° B.160° C.100° D.80°或100°
2.如图,将△OAB绕点O逆时针旋转80°,得到△OCD.若∠A=2∠D=100°,则∠α的度数是(?? )
A.?50°??????????????????????????????B.?60°??????????????????????????????C.?40°??????????????????????????????D.?30°
3.如图,平面直角坐标系中,已知点B ,若将△ABO绕点O沿顺时针方向旋转90°后得到△A1B1O,则点B的对应点B1的坐标是(???? )
A.?(3,1)??????????????????B.?(3,2)??????????????????C.?(1,3)??????????????????D.?(2,3)
4.如图,四边形 是⊙ 的内接正方形,点 是劣弧 上任意一点(与点 不重合),则 的度数为(?? )
A.?30°???????????????????????????B.?45°???????????????????????????C.?60°???????????????????????????D.?无法确定
5.已知圆的半径为3,扇形的圆心角为 ,则扇形的面积为 (?? )
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
6.如图,在正方形ABCD中,分别取AD、BC的中点E、F,并连接EF;以点F为圆心,FD的长为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则 的值为(?? )
A.? ?? ???C. ?? D.
7.如图,AB是⊙O的弦,AB=5,点C是⊙O上的一个动点,且∠ACB=45°,点M,N分别是AB,AC的中点,则线段MN长的最大值为( ??)
A.?5???????????????????????????B.?????????????????????????????C.?5 ???????????????????????????D.?
8.如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB’C’D’ , 图中阴影部分的面积为(?? ).
A.???????????????????????????B.???????????????????????C.???????????????????????D.?
9.如图,已知圆O的半径为10,AB⊥CD,垂足为P,且AB=CD=16,则OP的长为(?? )
A.?6?????????????????????????????B.?6 ??????????????????????????????C.?8??????????????????????????????D.?8
10.如图,在⊙O中,AB是⊙O的直径,AB=10, = = ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED= ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是(?? )
A.?1??????????????????????????????????B.?2??????????????????????????????????C.?3??????????????????????????????????D.?4
二、填空题(每小题4分,共24分)
11.如图,O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=38?,则∠OAC的度数是________.
12.如图,⊙O的半径为5,AB为弦,OC⊥AB,垂足为E,如果CE=2,那么AB的长是________
13.某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为________m.
14.为庆祝祖国华诞,某单位排练的节目需用到如图所示的扇形布扇,布扇完全打开后,外侧两竹条AB,AC夹角为120°,AB的长为30cm,贴布部分BD的长为20cm,则贴布部分的面积约为________cm2 .
15.如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,过E点作EH⊥CD于H,则EH的长为________.
16.如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,下列结论:①DM=CM;② ;③⊙O的直径为2;④AE=AD.其中正确的结论有________(填序号).
三、解答题(每小题6分,共18分)
17.如图,AB、CD是⊙O的直径,弦CE∥AB,弧 的度数为50°,求∠AOC的度数.
18.如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD , CD∥AB . 若⊙O的半径为1,求图中阴影部分的面积(结果保留π).
19.如图为桥洞的形状,其正视图是由 和矩形ABCD构成.O点为 所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F)EF为2米.求 所在⊙O的半径DO.
四,解答题(每小题8分,共48分)
20.如图,已知等腰直角△ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求 的值
21.如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1 .
(1)画出△A1OB1;
(2)在旋转过程中点B所经过的路径长为?? ? ? ? ? ? ? ? ? ?;
(3)求在旋转过程中线段AB、BO扫过的图形的面积之和.
22.如图,正方形ABCD的外接圆为⊙O,点P在劣弧 上(不与C点重合).
(1)求∠BPC的度数;
(2)若⊙O的半径为8,求正方形ABCD的边长.
23.已知:⊙O为Rt△ABC的外接圆,点D在边AC上,AD=AO;
(1)如图1,若弦BE∥OD,求证:OD=BE;
(2)如图2,点F在边BC上,BF=BO,若OD=2 ?, OF=3,求⊙O的直径.
24.如图,四边形ACBE内接于⊙O,AB平分∠CAE,CD⊥AB交AB、AE分别于点H、D.
(1)如图①,求证:BD=BE;
(2)如图②,若F是弧AC的中点,连接BF,交CD于点M,∠CMF=2∠CBF,连接FO、OC,求∠FOC的度数;
(3)在(2)的条件下,连接OD,若BC=4 ?,OD=7,求BF的长.
25.如图,在平面直角坐标系中,△AOB是直角三角形,∠AOB=90°,边AB与y轴交于点C.
(1)若∠A=∠AOC,试说明:∠B=∠BOC;
(2)延长AB交x轴于点E,过O作OD⊥AB,若∠DOB=∠EOB,∠A=∠E,求∠A的度数;
(3)如图,OF平分∠AOM,∠BCO的平分线交FO的延长线于点P,∠A=40°,当△ABO绕O点旋转时(边AB与y轴正半轴始终相交于点C),问∠P的度数是否发生改变?若不变,求其度数;若改变,请说明理由.
答案
一、选择题(每小题3分,共30分)
1. 解:∠ABC=∠AOC=×160°=80°或∠ABC=×(360°-160°)=100°.
故答案为:D.
2.解:根据旋转的意义,图片按逆时针方向旋转80°,可得∠AOC=80°,∠C=∠A,
∵∠A=2∠D=100°
∴∠A=100°,∠D=50°,
∴∠DOC=180°-∠C-∠D=30°,
∴∠a=∠AOC-∠DOC=50°
故答案为:A.
3.解:△A1B1O如图所示,点B1的坐标是(2,3).
故答案为:D.
4.解:连接OB,OC,
∵ 四边形 是⊙ 的内接正方形 ,
∴∠BOC==90°,
∴∠BPC=∠BOC=45°;
故答案为:? B.
5.解: 扇形的圆心角为 ,其半径为3,
。
故答案为:C。
6.
解:设正方形的边长为2,则CD=AB=2,CF=1
在直角三角形DCF中,DF== ,∴FG=EH= ,∴DH= -1
∴ = ,
故答案为:A.
7.解:∵ 点M,N分别是AB,AC的中点,
∴MN=BC,
∴当BC最大时,线段MN的长最大,
∴当BC为 ⊙O 直径时,BC长度最大,
∴∠BA=90°,
在Rt△BAC中,
∵ ∠ACB=45°, AB=5,
∴AC=5,BC==5
∴MN=BC= ,
即线段MN的长的最大值为.
故答案为:D.
8. 解:如图,设B′C′与CD的交点为E , 连接AE ,
在Rt△AB′E和Rt△ADE中,
,
∴Rt△AB′E≌Rt△ADE(HL),
∴∠DAE=∠B′AE ,
∵旋转角为30°,
∴∠DAB′=60°,
∴∠DAE= ×60°=30°,
∴DE=1× = ,
∴阴影部分的面积=1×1﹣2×( ×1× )=1﹣ .
故答案为:C .
9.解:作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,
∵AB=CD=16,
∴BM=DN=8,
∴OM=ON= =6,
∵AB⊥CD,
∴∠DPB=90°,
∵OM⊥AB于M,ON⊥CD于N,
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形,
∵OM=ON,
∴四边形MONP是正方形,
∴OP= .
故答案为:B.
10.解:∵ = = , 点E是点D关于AB的对称点,
∴ = ,
∴∠DOB=∠BOE=∠COD= =60°,∴①正确;
∠CED= ∠COD= =30°= ,∴②正确;
∵ 的度数是60°,
∴ 的度数是120°,
∴只有当M和A重合时,∠MDE=60°,
∵∠CED=30°,
∴只有M和A重合时,DM⊥CE,∴③错误;
做C关于AB的对称点F,连接CF,交AB于N,连接DF交AB于M,此时CM+DM的值最短,等于DF长,
连接CD,
∵ = = = ,并且弧的度数都是60°,
∴∠D= =60°,∠CFD= =30°,
∴∠FCD=180°﹣60°﹣30°=90°,
∴DF是⊙O的直径,
即DF=AB=10,
∴CM+DM的最小值是10,∴④正确;
答案为:C.
二、填空题(每小题4分,共24分)
11.解:∵∠AOB=38?,
∴∠ACB=19°,
又∵AO∥BC,
∴∠OAC=∠ACB=19°.
故答案为:19°.
12.解:如图,连接OA;
∵OC=5,CE=2,
∴OE=OC-CE=3,
∵ OC⊥AB ,
∴AB=2AE,
在Rt△AOE中,由勾股定理得:AE2+OE2=AO2 ,
又OA=5,OE=3,
∴AE=4,
∴AB=2AE=8;
故答案为8.
13.解:∵CD垂直平分AB,
∴AD=8.
∴OD= =6m,
∴CD=OC-OD=10-6=4(m).
14.解:贴布部分的面积=S扇形BAC-S扇形DAE
= -
= (cm2).
故答案为 .
15.解:∵△ABC为等边三角形,
∴∠BAC=60°,AB=AC,
∵将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,
∴∠DAE=∠BAC=60°,AD=AE=5,CE=BD=6,
∴△ADE为等边三角形,
∴DE=AD=5,
设DH=x,则CH=CD﹣DH=4﹣x,
在Rt△DHE中,EH2+x2=52 , ①
在Rt△CHE中,EH2+(4﹣x)2=62 , ②
②﹣①得16﹣8x=11,解得x= ,
∴EH= = .
故答案为 .
16.解:如下图,连接AM,连接MB,过点O作OG⊥AM,OH⊥AM,
∵∠BAD=∠CDA=90°,
∴AM过圆心O,而A、D、M、B四点共圆,
∴四边形ADMB为矩形,
∵AB=1,CD=2,
∴CM=2-1=1=AB=DM,
故①正确;
又∵AB∥CD,
∴四边形ABMC为平行四边形,
∴∠AEB=∠MAE, = ,
故②正确;
∵四边形ADMB为矩形,
∴AB=DM,
∴ = ,
∴= ,
∴∠DAM=∠EAM,
过点O作OG⊥AM,OH⊥AM,
∴OG=OH,
∴AD=AE,
故④正确;
由题设条件求不出直径的大小,
故③⊙O的直径为2,错误;
故答案为:①②④.
三、解答题(每小题6分,共18分)
17.解:连接OE,如图,
∵ 的度数为50°,
∴∠COE=50°,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OCE=(180°﹣50°)÷2=65°,
∵CE∥AB,
∴∠AOC=∠OCE=65°.
18.解:∵BC∥AD,CD∥AB,
∴四边形ABCD是平行四边形,
∴CD=AB=2,
∴S梯形OBCD==;
∴图中阴影部分的面积=S梯形OBCD-S扇形OBD=-×π×12=-。
四、解答题(每小题8分,共48分)
19. 解:∵OE⊥弦CD于点F,CD为8米,EF为2米,
∴EO垂直平分CD,DF=4m,FO=DO﹣2,
在Rt△DFO中,DO2=FO2+DF2 , 则DO2=(DO﹣2)2+42 , 解得:DO=5.
答:弧CD所在⊙O的半径DO为5m
20.(1)证明:∵△ABC是等腰直角三角形,
∴∠C=∠ABC=45°,
∴∠PEA=∠ABC=45°
又∵PE是⊙O的直径,
∴∠PAE=90°,
∴∠PEA=∠APE=45°,
∴ △APE是等腰直角三角形.
(2)解:∵△ABC是等腰直角三角形,
∴AC=AB,
同理AP=AE,
又∵∠CAB=∠PAE=90°,
∴∠CAP=∠BAE,
∴△CPA≌△BAE,
∴CP=BE,
在Rt△BPE中,∠PBE=90°,PE=2,
∴PB2+BE2=PE2,
∴CP2+PB2=PE2=4.
21.解:(1)△A1OB1如图所示;
(2)由勾股定理得,BO==,
所以,点B所经过的路径长==π;
故答案为:π.
(3)由勾股定理得,OA==,
∵AB所扫过的面积=S扇形A1OA+S△A1B1O﹣S扇形B1OB﹣S△AOB=S扇形A1OA﹣S扇形B1OB ,
BO扫过的面积=S扇形B1OB ,
∴线段AB、BO扫过的图形的面积之和=S扇形A1OA﹣S扇形B1OB+S扇形B1OB ,
=S扇形A1OA ,
=,
=π.
?
22. (1)解:连接OB,OC,∵四边形ABCD为正方形,∴∠BOC=90°,∴∠BPC= ∠BOC=45°;
(2)解:过点O作OE⊥BC于点E, ∵OB=OC,∠BOC=90°,∴∠OBE=45°,∴OE=BE,∵OE2+BE2=OB2 , ∴BE= ?∴BC=2BE=2×
23.(1)证明:连接AE交OD于点F.
∵AB为直径,
∴AE⊥BE,
∵BE∥OD,
∴AE⊥OD,
∵AD=AO,
∴AE平分∠CAB,
∴OD=2OF,
∵BE=2OF,
∴BE=OD;
(2)解:分别作弦BE∥OD,AH∥OF,连接AE,BH,AE与BH交于点P,
由(1)得:E为弧BC的中点,同理H为弧AC的中点,
∴∠HAE=∠HBE=45°,
∵AB为直径,
∴∠H=∠E=90°,
∴AP= AH,PE=BE,
∵点O为AB的中点,BE∥OD,
∴EB=OD= ,
∴PE=BE= ,同理AH=OF=3,
∴AP= ,在Rt△ABE中,AE= ,BE= ,
根据勾股定理得:AB= ,
则圆的直径为 .
24. (1)解:如图1,连接OB、OC、OE,
∵AB平分∠CAE,
∴∠CAB=∠BAE,
∴∠COB=∠BOE,
∴BC=BE,
∵CD⊥AB,
∴∠CHA=∠DHA=90°,
∵∠CAB=∠BAE,AH=AH,
∴△ACH≌△ADH,
∴CH=DH,
∴AB为线段CD的垂直平分线,
∴BC=BD,
∴BD=BE;
(2)解:∵F是弧AC的中点,
∴ ?,
∴∠CBF=∠ABF,
∵∠CMF=2∠CBF,
∴∠CMF=2∠ABF,
∵CD⊥AB,∠CMF=∠BMH,
∴∠BMH+∠ABF=90°,
∴∠ABF=30°,
∴∠CBF=30°,
∵∠FOC=2∠CBF,
∴∠FOC=60°
(3)解:如图3,连接OM,OB,作ON⊥BF于N,DK⊥OM于K,
由(2)可知:∠CBF=∠ABF=∠BCH=30°,
∴CM=BM,
在Rt△CBH中,∠BCH=30°,BC=4 ,
∴BH=2 ,CH=6,
在Rt△BHM中,∠MBH=30°,BH=2 ,
∴BM=4? HM=2,
∴CM=BM=4,
∵OC=OB,OM=OM,
∴△OMC≌△OMB,
∴∠CMO=∠BMO=120°,∠OMF=∠OMD=60°,
∵CH=DH=6,
∴DM=8,
在Rt△DMK中,∠KMD=60°,DM=8,
∴MK=4,DK=4 ,
在Rt△OKD中,
OD2=OK2+DK2 ,
∵OD=7,DK=4 ,
∴OK=1,
∴OM=5,
在Rt△OMN中,∠OMN=60°,OM=5,
MN= OM= ,
∴BN=BM+MN= ,
∵ON⊥BF,
∴BF=2BN=13.
25. (1)解:∵△AOB是直角三角形??
∴∠A+∠B=90°,∠AOC+∠BOC=90°???
∵∠A=∠AOC???? ∴∠B=∠BOC
(2)解:∵∠A+∠ABO=90°,∠DOB+∠ABO=90°
∴∠A=∠DOB??????? 即∠DOB=∠EOB=∠OAE=∠OEA
∵∠DOB+∠EOB+∠OEA=90°?????? ∴∠A=30°
(3)解:∠P的度数不变,∠P=25°.
∵∠AOM=90°-∠AOC,∠BCO=∠A+∠AOC
又OF平分∠AOM,CP平分∠BCO
∴∠FOM=45°- ∠AOC,∠PCO= ∠A+ ∠AOC
∴∠P=180°-(∠PCO+∠FOM+90°)=45°- ∠A=25°
的度数.
第3页 共4页 ◎ 第4页 共4页
同课章节目录
