浙教版九年级数学上册第3章 圆的基本性质3.1 圆随堂练习解析版
文档属性
| 名称 | 浙教版九年级数学上册第3章 圆的基本性质3.1 圆随堂练习解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 237.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-13 19:03:52 | ||
图片预览




文档简介
3.1 圆
一.填空题
1.(2018秋?滨海县期末)平面直角坐标系内的三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3), 确定一个圆,(填“能”或“不能”).
2.(2018秋?吴兴区期末)如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD是斜边AB上的高线,以点C为圆心,2.5为半径作圆,则点D在圆 (填“外”,“内”,“上”).
3.(2018秋?泰兴市校级期中)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为x的圆,使点A、B、C三点都在圆外,则x的取值范围是 .
4.(2018秋?汶上县期中)已知一点到圆上的最短距离是2,最长距离是4,则圆的半径为 .
5.(2019?赤峰一模)直角三角形的两直角边长分别为8和6,则此三角形的外接圆半径是 .
6.(2018秋?京口区校级月考)如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,以B为圆心,BC长为半径的圆弧交AB于点D.若B、C、D三点中只有一点在⊙A内,则⊙A的半径r的取值范围是 .
二.选择题
7.(2018秋?鄞州区期末)已知AB是半径为5的圆的一条弦,则AB的长不可能是( )
A.4 B.8 C.10 D.12
8.(2019?嘉定区一模)已知点C在线段AB上(点C与点A、B不重合),过点A、B的圆记作为圆O1,过点B、C的圆记作为圆O2,过点C、A的圆记作为圆O3,则下列说法中正确的是( )
A.圆O1可以经过点C B.点C可以在圆O1的内部
C.点A可以在圆O2的内部 D.点B可以在圆O3的内部
9.(2018秋?潮南区期末)已知⊙O中最长的弦为8cm,则⊙O的半径为( )cm.
A.2 B.4 C.8 D.16
10.(2019春?巨野县期末)已知⊙O的半径为6cm,P为线段OA的中点,若点P在⊙O上,则OA的长( )
A.等于6cm B.等于12cm C.小于6cm D.大于12cm
11.(2018秋?天心区校级月考)下列说法中,错误的是( )
A.半圆是弧 B.半径相等的圆是等圆
C.过圆心的线段是直径 D.直径是弦
12.(2018秋?常熟市期末)已知⊙O的半径为4cm.若点P到圆心O的距离为3cm,则点P( )
A.在⊙O内 B.在⊙O上
C.在⊙O外 D.与⊙O的位置关系无法确定
13.(2018秋?安庆期末)在平面直角坐标系中,⊙O的圆心在点(1,0),半径为2,则下面各点在⊙O上的是( )
A.(2,0) B.(0,2) C.(0,) D.(,0)
14.(2018秋?城厢区期末)在平面直角坐标系xOy中,若点P(4,3)在⊙O内,则⊙O的半径r的取值范围是( )
A.0<r<4 B.3<r<4 C.4<r<5 D.r>5
15.(2019?金山区一模)如图,在Rt△ABC中,∠C=90°,BC=2,∠B=60°,⊙A的半径为3,那么下列说法正确的是( )
A.点B、点C都在⊙A内 B.点C在⊙A内,点B在⊙A外
C.点B在⊙A内,点C在⊙A外 D.点B、点C都在⊙A外
16.(2016秋?柯桥区校级月考)小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )
A.第一块 B.第二块 C.第三块 D.第四块
三.解答题
17.(2017秋?休宁县期中)如图,已知矩形ABCD的边AB=3cm,BC=4cm,以点A为圆心,4cm为半径作⊙A,则点B,C,D与⊙A怎样的位置关系.
18.已知:如图,△ABC中,∠C=90°,AC=2cm,BC=4cm,CM是中线,以C为圆心,以cm长为半径画圆,则点A、B、M与⊙C的关系如何?
19.如图,在△ABC中,∠ABC=90°,AB=4cm,AC=6cm,AM是中线.
(1)以A为圆心,4cm长为半径作⊙A,则点B、C、M与⊙A是什么位置关系?
(2)若以A为圆心作⊙A,使点B、C、M三点中至少有一点在圆内,且至少有一点在圆外,则⊙A的半径r的取值范围是什么?
20.(2018秋?微山县期中)小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点
P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用勾股定理得到结论:P1P2=;他还证明了线段P1P2的中点P(x,y)的坐标公式是:x=,y=;
启发应用
请利用上面的信息,解答下面的问题:
如图,在平面直角坐标系中,已知A(8,0),B(0,6),C(1,7),⊙M经过原点O及点A、B.
(1)求⊙M的半径及圆心M的坐标;
(2)判断点C与⊙M的位置关系,并说明理由.
21.如图,已知直线l和A,B两点,求作经过A,B两点的圆,使圆心在直线l上.
22.如图.已知点A(1,2)、B(4,1)、C(8,3).利用坐标网格和你的观察力.请直按说出△ABC外心的坐标和外接圆半径.
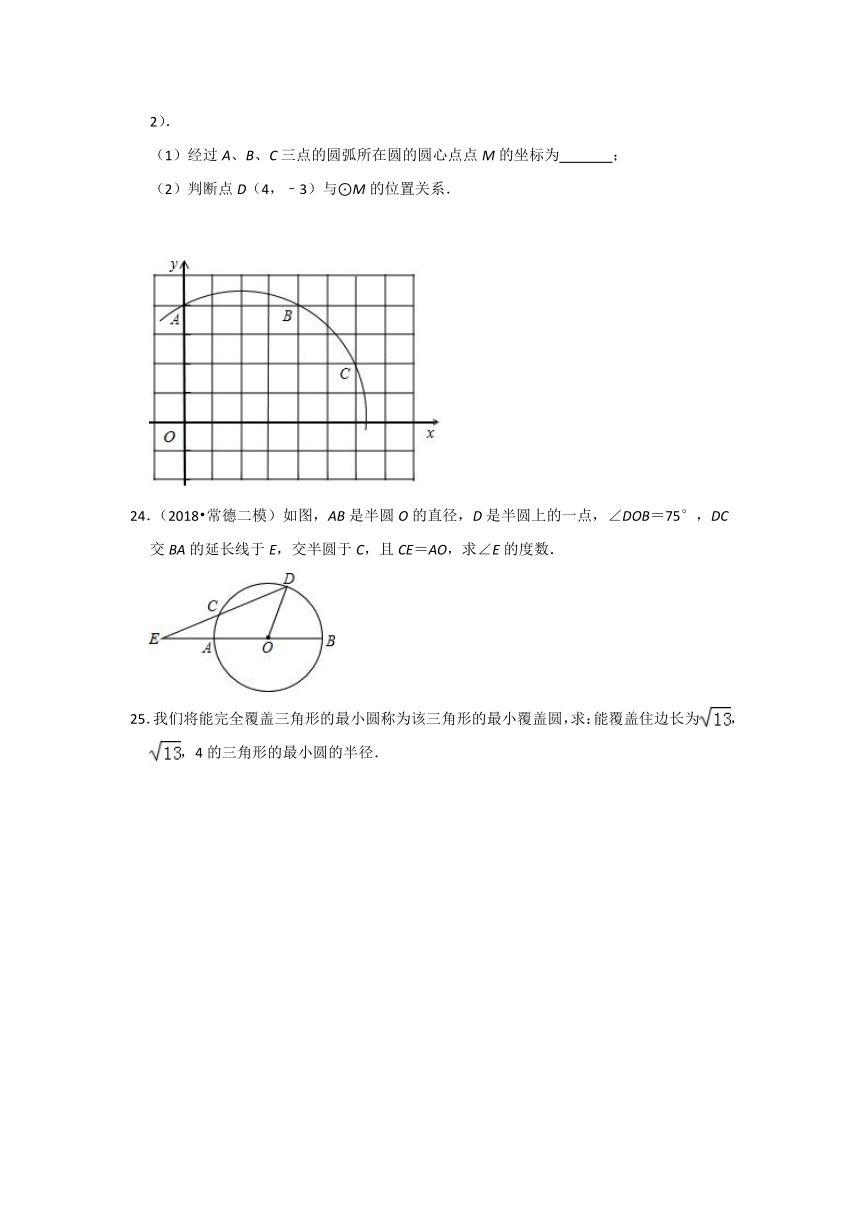
23.(2018秋?兴化市校级月考)如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)经过A、B、C三点的圆弧所在圆的圆心点点M的坐标为 ;
(2)判断点D(4,﹣3)与⊙M的位置关系.
24.(2018?常德二模)如图,AB是半圆O的直径,D是半圆上的一点,∠DOB=75°,DC交BA的延长线于E,交半圆于C,且CE=AO,求∠E的度数.
25.我们将能完全覆盖三角形的最小圆称为该三角形的最小覆盖圆,求:能覆盖住边长为,,4的三角形的最小圆的半径.
参考答案
一.填空题
1.(2018秋?滨海县期末)平面直角坐标系内的三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3), 不能 确定一个圆,(填“能”或“不能”).
【思路点拨】根据三个点的坐标特征得到它们共线,于是根据确定圆的条件可判断它们不能确定一个圆.
【答案】解:∵B(0,﹣3)、C(2,﹣3),
∴BC∥x轴,
而点A(1,﹣3)在x轴上,
∴点A、B、C共线,
∴三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3)不能确定一个圆.
故答案为:不能.
【点睛】本题考查了确定圆的条件:不在同一直线上的三点确定一个圆.
2.(2018秋?吴兴区期末)如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD是斜边AB上的高线,以点C为圆心,2.5为半径作圆,则点D在圆 内 (填“外”,“内”,“上”).
【思路点拨】直角三角形中根据勾股定理可以计算AB的长度,CD为AB边上的高,根据面积法AC×BC=AB×DC可以求得CD的长,与半径比较后即可得到点D与圆的位置关系.
【答案】解:直角△ABC中,AB2=AC2+BC2,
AC=4,BC=3,
∴AB==5,
△ABC的面积S=?AC?BC=?AB?CD
CD=.
∵<2.5,
∴点D在⊙C内,
故答案为:内.
【点睛】本题考查了直角三角形中勾股定理的运用及点与圆的位置关系,根据勾股定理计算斜边长是解题的关键.
3.(2018秋?泰兴市校级期中)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为x的圆,使点A、B、C三点都在圆外,则x的取值范围是 x<3 .
【思路点拨】要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
【答案】解:在直角△ABD中,CD=AB=4,AD=3,
则BD==5.
∵点A、B、C三点都在圆外,
∴x<3.
故答案为:x<3;
【点睛】此题主要考查了点与圆的位置关系,解决本题要注意点与圆的位置关系,要熟悉勾股定理,及点与圆的位置关系.
4.(2018秋?汶上县期中)已知一点到圆上的最短距离是2,最长距离是4,则圆的半径为 1或3 .
【思路点拨】根据已知条件能求出圆的直径,即可求出半径.
【答案】解:当点P在圆外时:
∵圆外一点和圆周的最短距离为2,最长距离为4,
∴圆的直径为4﹣2=2,
∴该圆的半径是1.
当点P在圆内时:
∵到圆上的最短距离是2,最长距离是4,
∴该圆的直径为4+2=6,
∴该圆的半径为3,
∴圆的半径为1或3,
故答案为:1或3.
【点睛】本题考查了点和圆的位置关系的应用,能根据已知条件求出圆的直径是解此题的关键.
5.(2019?赤峰一模)直角三角形的两直角边长分别为8和6,则此三角形的外接圆半径是 5 .
【思路点拨】根据直角三角形外接圆的圆心是斜边的中点,由勾股定理求得斜边,即可得出答案.
【答案】解:如图,∵AC=8,BC=6,
∴AB==10,
∴外接圆半径为5.
故答案为:5.
【点睛】本题考查了三角形的外接圆以及外心,注意:直角三角形的外心是斜边的中点.
6.(2018秋?京口区校级月考)如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,以B为圆心,BC长为半径的圆弧交AB于点D.若B、C、D三点中只有一点在⊙A内,则⊙A的半径r的取值范围是 2<r≤4 .
【思路点拨】先根据勾股定理AB的长,然后由B,C,D与⊙A的位置,确定⊙A的半径的取值范围.
【答案】解:由勾股定理得到:AB==5,
则AD=AB﹣BD=5﹣3=2,
∵B、C、D三点中只有一点在⊙A内,AC=4,
∴⊙A的半径r的取值范围是2<r≤4.
故答案是:2<r≤4.
【点睛】本题考查的是勾股定理、点与圆的位置关系,要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
二.选择题
7.(2018秋?鄞州区期末)已知AB是半径为5的圆的一条弦,则AB的长不可能是( )
A.4 B.8 C.10 D.12
【思路点拨】根据圆中最长的弦为直径求解.
【答案】解:因为圆中最长的弦为直径,所以弦长L≤10.
故选:D.
【点睛】考查了圆的认识,在本题中,圆的弦长的取值范围0<L≤10.
8.(2019?嘉定区一模)已知点C在线段AB上(点C与点A、B不重合),过点A、B的圆记作为圆O1,过点B、C的圆记作为圆O2,过点C、A的圆记作为圆O3,则下列说法中正确的是( )
A.圆O1可以经过点C B.点C可以在圆O1的内部
C.点A可以在圆O2的内部 D.点B可以在圆O3的内部
【思路点拨】根据已知条件对个选项进行判断即可.
【答案】解:∵点C在线段AB上(点C与点A、B不重合),过点A、B的圆记作为圆O1,
∴点C可以在圆O1的内部,故A错误,B正确;
∵过点B、C的圆记作为圆O2,
∴点A可以在圆O2的外部,故C错误;
∵过点C、A的圆记作为圆O3,
∴点B可以在圆O3的外部,故D错误.
故选:B.
【点睛】本题考查了圆的认识,根据已知条件正确的作出判断是解题的关键.
9.(2018秋?潮南区期末)已知⊙O中最长的弦为8cm,则⊙O的半径为( )cm.
A.2 B.4 C.8 D.16
【思路点拨】⊙O最长的弦就是直径从而不难求得半径的长.
【答案】解:∵⊙O中最长的弦为8cm,即直径为8cm,
∴⊙O的半径为4cm.
故选:B.
【点睛】本题考查弦,直径等知识,记住圆中的最长的弦就是直径是解题的关键.
10.(2019春?巨野县期末)已知⊙O的半径为6cm,P为线段OA的中点,若点P在⊙O上,则OA的长( )
A.等于6cm B.等于12cm C.小于6cm D.大于12cm
【思路点拨】点在圆上,则d=r;点在圆外,d>r;点在圆内,d<r(d即点到圆心的距离,r即圆的半径).
【答案】解:根据点和圆的位置关系,得OP=6,再根据线段的中点的概念,得OA=2OP=12.
故选:B.
【点睛】注意点和圆的位置关系与数量之间的等价关系是解决问题的关键.
11.(2018秋?天心区校级月考)下列说法中,错误的是( )
A.半圆是弧 B.半径相等的圆是等圆
C.过圆心的线段是直径 D.直径是弦
【思路点拨】根据圆的有关概念进行判断.
【答案】解:A、半圆是弧,所以A选项的说法正确;
B、半径相等的圆是等圆,所以B选项的说法正确;
C、过圆心的弦为直径,所以C选项的说法错误;
D、直径是弦,所以D选项的说法正确.
故选:C.
【点睛】本题考查了圆的认识:熟练掌握与圆有关的概念( 弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).
12.(2018秋?常熟市期末)已知⊙O的半径为4cm.若点P到圆心O的距离为3cm,则点P( )
A.在⊙O内 B.在⊙O上
C.在⊙O外 D.与⊙O的位置关系无法确定
【思路点拨】直接根据点与圆的位置关系进行判断.
【答案】解:∵点P到圆心的距离为3cm,
而⊙O的半径为4cm,
∴点P到圆心的距离小于圆的半径,
∴点P在圆内,
故选:A.
【点睛】本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.
13.(2018秋?安庆期末)在平面直角坐标系中,⊙O的圆心在点(1,0),半径为2,则下面各点在⊙O上的是( )
A.(2,0) B.(0,2) C.(0,) D.(,0)
【思路点拨】根据点的坐标性质结合勾股定理得出斜边长,进而得出点与⊙O关系.
【答案】解:A、点(2,0)到⊙O的圆心(1,0)的距离为:2﹣1=1<2,所以点(2,0)在⊙O内,错误;
B、点(0,2)到⊙O的圆心(1,0)的距离为:>2,所以点(2,0)在⊙O外,错误;
C、点(0,)到⊙O的圆心(1,0)的距离为:=2,所以点(2,0)在⊙O上,正确;
D、点(,0)到⊙O的圆心(1,0)的距离为:﹣1<2,所以点(2,0)在⊙O内,错误;
故选:C.
【点睛】此题主要考查了点与圆的位置关系,点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点P在圆外d>r,②点P在圆上d=r,③点P在圆内d<r.
14.(2018秋?城厢区期末)在平面直角坐标系xOy中,若点P(4,3)在⊙O内,则⊙O的半径r的取值范围是( )
A.0<r<4 B.3<r<4 C.4<r<5 D.r>5
【思路点拨】本题可先由勾股定理等性质算出点与圆心的距离d,再根据点与圆心的距离与半径的大小关系,即当d>r时,点在圆外;当d=r时,点在圆上;点在圆外;当d<r时,点在圆内;来确定点与圆的位置关系.
【答案】解:∵点P(4,3),
∴PO==5,
∵点P在⊙O内,
∴r>OP,即r>5,
故选:D.
【点睛】本题主要考查点与圆的位置关系,解题的关键是能够根据勾股定理求得点到圆心的距离,根据数量关系判断点和圆的位置关系.
15.(2019?金山区一模)如图,在Rt△ABC中,∠C=90°,BC=2,∠B=60°,⊙A的半径为3,那么下列说法正确的是( )
A.点B、点C都在⊙A内 B.点C在⊙A内,点B在⊙A外
C.点B在⊙A内,点C在⊙A外 D.点B、点C都在⊙A外
【思路点拨】先解直角△ABC,求出AB、AC的长,再根据点到圆心距离与半径的关系可以确定点B、点C与⊙A的位置关系.
【答案】解:∵在Rt△ABC中,∠C=90°,BC=2,∠B=60°,
∴∠A=30°,
∴AB=2BC=4,AC=BC=2,
∵⊙A的半径为3,4>3,2>3,
∴点B、点C都在⊙A外.
故选:D.
【点睛】本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.也考查了含30°角的直角三角形的性质.
16.(2016秋?柯桥区校级月考)小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )
A.第一块 B.第二块 C.第三块 D.第四块
【思路点拨】要确定圆的大小需知道其半径.根据垂径定理知第①块可确定半径的大小.
【答案】解:第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
【点睛】本题考查了确定圆的条件,解题的关键是熟练掌握:圆上任意两弦的垂直平分线的交点即为该圆的圆心.
三.解答题
17.(2017秋?休宁县期中)如图,已知矩形ABCD的边AB=3cm,BC=4cm,以点A为圆心,4cm为半径作⊙A,则点B,C,D与⊙A怎样的位置关系.
【思路点拨】连接AC,根据勾股定理求出AC的长,进而得出点B,C,D与⊙A的位置关系.
【答案】解:连接AC
,
∵AB=3cm,BC=AD=4cm,
∴AC=5cm,
∴点B在⊙A内,点D在⊙A上,点C在⊙A外.
【点睛】此题主要考查了点与圆的位置关系,解决本题要注意点与圆的位置关系,要熟悉勾股定理,及点与圆的位置关系.
18.已知:如图,△ABC中,∠C=90°,AC=2cm,BC=4cm,CM是中线,以C为圆心,以cm长为半径画圆,则点A、B、M与⊙C的关系如何?
【思路点拨】点与圆的位置关系由三种情况:设点到圆心的距离为d,则当d=R时,点在圆上;当d>R时,点在圆外;当d<R时,点在圆内.
【答案】解:根据勾股定理,有AB==2(cm);
∵CA=2cm<cm,
∴点A在⊙O内,
∵BC=4cm>cm,
∴点B在⊙C外;
由中线定理得:CM=cm
∴M点在⊙C上.
【点睛】本题主要考查了点与圆的位置关系.
19.如图,在△ABC中,∠ABC=90°,AB=4cm,AC=6cm,AM是中线.
(1)以A为圆心,4cm长为半径作⊙A,则点B、C、M与⊙A是什么位置关系?
(2)若以A为圆心作⊙A,使点B、C、M三点中至少有一点在圆内,且至少有一点在圆外,则⊙A的半径r的取值范围是什么?
【思路点拨】(1)根据点与圆的位置关系判定方法,比较AB,AC,AM与AB的大小关系即可得出答案;
(2)利用分界点当B、C、M三点中至少有一点在⊙A内时,以及当至少有一点在⊙A外时,分别求出即可.
【答案】解:(1)∵AB=4cm=⊙A的半径,
∴点B在⊙A上;
∵AC=6cm>4cm,
∴点C在⊙A外;
由勾股定理,得BC==2cm,
∵AM是BC边上的中线,
∴AM=BC=cm<4cm,
∴点M在⊙A内;
(2)以点A为圆心作⊙A,使B、C、M三点中至少有一点在⊙A内时,r>cm,
当至少有一点在⊙A外时,r<6cm,
故⊙A的半径r的取值范围为:cm<r<6cm.
【点睛】此题主要考查了点与圆的位置关系
20.(2018秋?微山县期中)小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用勾股定理得到结论:P1P2=
;他还证明了线段P1P2的中点P(x,y)的坐标公式是:x=,y=;
启发应用
请利用上面的信息,解答下面的问题:
如图,在平面直角坐标系中,已知A(8,0),B(0,6),C(1,7),⊙M经过原点O及点A、B.
(1)求⊙M的半径及圆心M的坐标;
(2)判断点C与⊙M的位置关系,并说明理由.
【思路点拨】(1)先确定出AB=10,进而求出圆M的半径,最后用线段的中点坐标公式即可得出结论;
(2)求出CM=5和圆M的半径比较大小,即可得出结论.
【答案】解:(1)∵∠AOB=90°,
∴AB是⊙M的直径,
∵A(8,0),B(0,6),
∴AB==10,
∴⊙M的半径为5,
由线段中点坐标公式x=,y=,得x=4,y=3,
∴M(4,3),
(2)点C在⊙M上,
理由:∵C(1,7),M(4,3),
∴CM==5,
∴点C在⊙M上.
【点睛】本题主要考查了点与圆的位置关系,解题的关键是对两点间的距离公式的理解和掌握,灵活运用线段中点坐标公式和两点间距离公式.
21.如图,已知直线l和A,B两点,求作经过A,B两点的圆,使圆心在直线l上.
【思路点拨】连接AB,作出AB的垂直平分线交直线l于O点,以O为圆心,OA为半径作圆.
【答案】解:如图所示,⊙O即为所求.
【点睛】本题主要考查确定圆的条件的知识点,本题要求有较强的作图能力,对同学来说需要熟练掌握.
22.如图.已知点A(1,2)、B(4,1)、C(8,3).利用坐标网格和你的观察力.请直按说出△ABC外心的坐标和外接圆半径.
【思路点拨】作CD⊥AB于D,点O为外心,根据图形和坐标的性质得到AD和CD的长度,根据外心的概念和勾股定理列出方程,解方程得到答案.
【答案】解:分别作AB、BC的垂直平分线交于点P,
由图形可知,点P的坐标为:(4,6),
外接圆的半径为5.
答:△ABC外心的坐标为(4,6),外接圆半径为5.
【点睛】本题考查的是坐标与图形的性质、三角形的外心的性质和勾股定理的应用,正确根据坐标求出线段的长度、根据题意列出方程是解题的关键.
23.(2018秋?兴化市校级月考)如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)经过A、B、C三点的圆弧所在圆的圆心点M的坐标为 (2,0) ;
(2)判断点D(4,﹣3)与⊙M的位置关系.
【思路点拨】(1)根据垂径定理的推论:弦的垂直平分线必过圆心,可以作弦AB和BC的垂直平分线,交点即为圆心.
(2)求出⊙M的半径,MD的长即可判断;
【答案】解:(1)根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,0)
故答案为:2,0.
(2)圆的半径AM==2,
线段MD==<2,
所以点D在⊙M内.
【点睛】本题主要考查确定圆的条件和坐标与图形性质的知识点,点与圆的位置关系等知识,能够根据垂径定理的推论得到圆心的位置是解决问题的关键.
24.(2018?常德二模)如图,AB是半圆O的直径,D是半圆上的一点,∠DOB=75°,DC交BA的延长线于E,交半圆于C,且CE=AO,求∠E的度数.
【思路点拨】连结OC,如图,由CE=AO,OA=OC得到OC=EC,则根据等腰三角形的性质得∠E=∠1,再利用三角形外角性质得∠2=∠E+∠1=2∠E,加上∠D=∠2=2∠E,
所以∠BOD=∠E+∠D,即∠E+2∠E=75°,然后解方程即可.
【答案】解:连结OC,如图,
∵CE=AO,
而OA=OC,
∴OC=EC,
∴∠E=∠1,
∴∠2=∠E+∠1=2∠E,
∵OC=OD,
∴∠D=∠2=2∠E,
∵∠BOD=∠E+∠D,
∴∠E+2∠E=75°,
∴∠E=25°.
【点睛】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质.
25.我们将能完全覆盖三角形的最小圆称为该三角形的最小覆盖圆,求:能覆盖住边长为,,4的三角形的最小圆的半径.
【思路点拨】根据等腰三角形的三边长可知,此等腰三角形是锐角三角形,因此能盖住三角形的最小圆应该是三角形的外接圆;可过等腰三角形的顶角顶点作圆的直径,通过勾股定理和相交弦定理求出此圆的外接圆半径.
【答案】解:如图;△ABC中,AB=AC=,BC=4;
由于△ABC是锐角三角形,因此能覆盖此三角形的最小圆应该是△ABC的外接圆⊙O;
过A作⊙O的直径AE,交BC于D;
在Rt△ABD中,AB=,BD=2,
由勾股定理得:AD=3;
由相交弦定理知:BD2=AD?DE,即DE=BD2÷AD=;
故⊙O的半径最小为:(AD+DE)=×(3+)=.
【点睛】此题考查了等腰三角形的性质、勾股定理、垂径定理、相交弦定理等知识的综合应用,首先判断出△ABC的形状是解题的关键.
一.填空题
1.(2018秋?滨海县期末)平面直角坐标系内的三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3), 确定一个圆,(填“能”或“不能”).
2.(2018秋?吴兴区期末)如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD是斜边AB上的高线,以点C为圆心,2.5为半径作圆,则点D在圆 (填“外”,“内”,“上”).
3.(2018秋?泰兴市校级期中)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为x的圆,使点A、B、C三点都在圆外,则x的取值范围是 .
4.(2018秋?汶上县期中)已知一点到圆上的最短距离是2,最长距离是4,则圆的半径为 .
5.(2019?赤峰一模)直角三角形的两直角边长分别为8和6,则此三角形的外接圆半径是 .
6.(2018秋?京口区校级月考)如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,以B为圆心,BC长为半径的圆弧交AB于点D.若B、C、D三点中只有一点在⊙A内,则⊙A的半径r的取值范围是 .
二.选择题
7.(2018秋?鄞州区期末)已知AB是半径为5的圆的一条弦,则AB的长不可能是( )
A.4 B.8 C.10 D.12
8.(2019?嘉定区一模)已知点C在线段AB上(点C与点A、B不重合),过点A、B的圆记作为圆O1,过点B、C的圆记作为圆O2,过点C、A的圆记作为圆O3,则下列说法中正确的是( )
A.圆O1可以经过点C B.点C可以在圆O1的内部
C.点A可以在圆O2的内部 D.点B可以在圆O3的内部
9.(2018秋?潮南区期末)已知⊙O中最长的弦为8cm,则⊙O的半径为( )cm.
A.2 B.4 C.8 D.16
10.(2019春?巨野县期末)已知⊙O的半径为6cm,P为线段OA的中点,若点P在⊙O上,则OA的长( )
A.等于6cm B.等于12cm C.小于6cm D.大于12cm
11.(2018秋?天心区校级月考)下列说法中,错误的是( )
A.半圆是弧 B.半径相等的圆是等圆
C.过圆心的线段是直径 D.直径是弦
12.(2018秋?常熟市期末)已知⊙O的半径为4cm.若点P到圆心O的距离为3cm,则点P( )
A.在⊙O内 B.在⊙O上
C.在⊙O外 D.与⊙O的位置关系无法确定
13.(2018秋?安庆期末)在平面直角坐标系中,⊙O的圆心在点(1,0),半径为2,则下面各点在⊙O上的是( )
A.(2,0) B.(0,2) C.(0,) D.(,0)
14.(2018秋?城厢区期末)在平面直角坐标系xOy中,若点P(4,3)在⊙O内,则⊙O的半径r的取值范围是( )
A.0<r<4 B.3<r<4 C.4<r<5 D.r>5
15.(2019?金山区一模)如图,在Rt△ABC中,∠C=90°,BC=2,∠B=60°,⊙A的半径为3,那么下列说法正确的是( )
A.点B、点C都在⊙A内 B.点C在⊙A内,点B在⊙A外
C.点B在⊙A内,点C在⊙A外 D.点B、点C都在⊙A外
16.(2016秋?柯桥区校级月考)小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )
A.第一块 B.第二块 C.第三块 D.第四块
三.解答题
17.(2017秋?休宁县期中)如图,已知矩形ABCD的边AB=3cm,BC=4cm,以点A为圆心,4cm为半径作⊙A,则点B,C,D与⊙A怎样的位置关系.
18.已知:如图,△ABC中,∠C=90°,AC=2cm,BC=4cm,CM是中线,以C为圆心,以cm长为半径画圆,则点A、B、M与⊙C的关系如何?
19.如图,在△ABC中,∠ABC=90°,AB=4cm,AC=6cm,AM是中线.
(1)以A为圆心,4cm长为半径作⊙A,则点B、C、M与⊙A是什么位置关系?
(2)若以A为圆心作⊙A,使点B、C、M三点中至少有一点在圆内,且至少有一点在圆外,则⊙A的半径r的取值范围是什么?
20.(2018秋?微山县期中)小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点
P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用勾股定理得到结论:P1P2=;他还证明了线段P1P2的中点P(x,y)的坐标公式是:x=,y=;
启发应用
请利用上面的信息,解答下面的问题:
如图,在平面直角坐标系中,已知A(8,0),B(0,6),C(1,7),⊙M经过原点O及点A、B.
(1)求⊙M的半径及圆心M的坐标;
(2)判断点C与⊙M的位置关系,并说明理由.
21.如图,已知直线l和A,B两点,求作经过A,B两点的圆,使圆心在直线l上.
22.如图.已知点A(1,2)、B(4,1)、C(8,3).利用坐标网格和你的观察力.请直按说出△ABC外心的坐标和外接圆半径.
23.(2018秋?兴化市校级月考)如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)经过A、B、C三点的圆弧所在圆的圆心点点M的坐标为 ;
(2)判断点D(4,﹣3)与⊙M的位置关系.
24.(2018?常德二模)如图,AB是半圆O的直径,D是半圆上的一点,∠DOB=75°,DC交BA的延长线于E,交半圆于C,且CE=AO,求∠E的度数.
25.我们将能完全覆盖三角形的最小圆称为该三角形的最小覆盖圆,求:能覆盖住边长为,,4的三角形的最小圆的半径.
参考答案
一.填空题
1.(2018秋?滨海县期末)平面直角坐标系内的三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3), 不能 确定一个圆,(填“能”或“不能”).
【思路点拨】根据三个点的坐标特征得到它们共线,于是根据确定圆的条件可判断它们不能确定一个圆.
【答案】解:∵B(0,﹣3)、C(2,﹣3),
∴BC∥x轴,
而点A(1,﹣3)在x轴上,
∴点A、B、C共线,
∴三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3)不能确定一个圆.
故答案为:不能.
【点睛】本题考查了确定圆的条件:不在同一直线上的三点确定一个圆.
2.(2018秋?吴兴区期末)如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD是斜边AB上的高线,以点C为圆心,2.5为半径作圆,则点D在圆 内 (填“外”,“内”,“上”).
【思路点拨】直角三角形中根据勾股定理可以计算AB的长度,CD为AB边上的高,根据面积法AC×BC=AB×DC可以求得CD的长,与半径比较后即可得到点D与圆的位置关系.
【答案】解:直角△ABC中,AB2=AC2+BC2,
AC=4,BC=3,
∴AB==5,
△ABC的面积S=?AC?BC=?AB?CD
CD=.
∵<2.5,
∴点D在⊙C内,
故答案为:内.
【点睛】本题考查了直角三角形中勾股定理的运用及点与圆的位置关系,根据勾股定理计算斜边长是解题的关键.
3.(2018秋?泰兴市校级期中)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为x的圆,使点A、B、C三点都在圆外,则x的取值范围是 x<3 .
【思路点拨】要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
【答案】解:在直角△ABD中,CD=AB=4,AD=3,
则BD==5.
∵点A、B、C三点都在圆外,
∴x<3.
故答案为:x<3;
【点睛】此题主要考查了点与圆的位置关系,解决本题要注意点与圆的位置关系,要熟悉勾股定理,及点与圆的位置关系.
4.(2018秋?汶上县期中)已知一点到圆上的最短距离是2,最长距离是4,则圆的半径为 1或3 .
【思路点拨】根据已知条件能求出圆的直径,即可求出半径.
【答案】解:当点P在圆外时:
∵圆外一点和圆周的最短距离为2,最长距离为4,
∴圆的直径为4﹣2=2,
∴该圆的半径是1.
当点P在圆内时:
∵到圆上的最短距离是2,最长距离是4,
∴该圆的直径为4+2=6,
∴该圆的半径为3,
∴圆的半径为1或3,
故答案为:1或3.
【点睛】本题考查了点和圆的位置关系的应用,能根据已知条件求出圆的直径是解此题的关键.
5.(2019?赤峰一模)直角三角形的两直角边长分别为8和6,则此三角形的外接圆半径是 5 .
【思路点拨】根据直角三角形外接圆的圆心是斜边的中点,由勾股定理求得斜边,即可得出答案.
【答案】解:如图,∵AC=8,BC=6,
∴AB==10,
∴外接圆半径为5.
故答案为:5.
【点睛】本题考查了三角形的外接圆以及外心,注意:直角三角形的外心是斜边的中点.
6.(2018秋?京口区校级月考)如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,以B为圆心,BC长为半径的圆弧交AB于点D.若B、C、D三点中只有一点在⊙A内,则⊙A的半径r的取值范围是 2<r≤4 .
【思路点拨】先根据勾股定理AB的长,然后由B,C,D与⊙A的位置,确定⊙A的半径的取值范围.
【答案】解:由勾股定理得到:AB==5,
则AD=AB﹣BD=5﹣3=2,
∵B、C、D三点中只有一点在⊙A内,AC=4,
∴⊙A的半径r的取值范围是2<r≤4.
故答案是:2<r≤4.
【点睛】本题考查的是勾股定理、点与圆的位置关系,要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
二.选择题
7.(2018秋?鄞州区期末)已知AB是半径为5的圆的一条弦,则AB的长不可能是( )
A.4 B.8 C.10 D.12
【思路点拨】根据圆中最长的弦为直径求解.
【答案】解:因为圆中最长的弦为直径,所以弦长L≤10.
故选:D.
【点睛】考查了圆的认识,在本题中,圆的弦长的取值范围0<L≤10.
8.(2019?嘉定区一模)已知点C在线段AB上(点C与点A、B不重合),过点A、B的圆记作为圆O1,过点B、C的圆记作为圆O2,过点C、A的圆记作为圆O3,则下列说法中正确的是( )
A.圆O1可以经过点C B.点C可以在圆O1的内部
C.点A可以在圆O2的内部 D.点B可以在圆O3的内部
【思路点拨】根据已知条件对个选项进行判断即可.
【答案】解:∵点C在线段AB上(点C与点A、B不重合),过点A、B的圆记作为圆O1,
∴点C可以在圆O1的内部,故A错误,B正确;
∵过点B、C的圆记作为圆O2,
∴点A可以在圆O2的外部,故C错误;
∵过点C、A的圆记作为圆O3,
∴点B可以在圆O3的外部,故D错误.
故选:B.
【点睛】本题考查了圆的认识,根据已知条件正确的作出判断是解题的关键.
9.(2018秋?潮南区期末)已知⊙O中最长的弦为8cm,则⊙O的半径为( )cm.
A.2 B.4 C.8 D.16
【思路点拨】⊙O最长的弦就是直径从而不难求得半径的长.
【答案】解:∵⊙O中最长的弦为8cm,即直径为8cm,
∴⊙O的半径为4cm.
故选:B.
【点睛】本题考查弦,直径等知识,记住圆中的最长的弦就是直径是解题的关键.
10.(2019春?巨野县期末)已知⊙O的半径为6cm,P为线段OA的中点,若点P在⊙O上,则OA的长( )
A.等于6cm B.等于12cm C.小于6cm D.大于12cm
【思路点拨】点在圆上,则d=r;点在圆外,d>r;点在圆内,d<r(d即点到圆心的距离,r即圆的半径).
【答案】解:根据点和圆的位置关系,得OP=6,再根据线段的中点的概念,得OA=2OP=12.
故选:B.
【点睛】注意点和圆的位置关系与数量之间的等价关系是解决问题的关键.
11.(2018秋?天心区校级月考)下列说法中,错误的是( )
A.半圆是弧 B.半径相等的圆是等圆
C.过圆心的线段是直径 D.直径是弦
【思路点拨】根据圆的有关概念进行判断.
【答案】解:A、半圆是弧,所以A选项的说法正确;
B、半径相等的圆是等圆,所以B选项的说法正确;
C、过圆心的弦为直径,所以C选项的说法错误;
D、直径是弦,所以D选项的说法正确.
故选:C.
【点睛】本题考查了圆的认识:熟练掌握与圆有关的概念( 弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).
12.(2018秋?常熟市期末)已知⊙O的半径为4cm.若点P到圆心O的距离为3cm,则点P( )
A.在⊙O内 B.在⊙O上
C.在⊙O外 D.与⊙O的位置关系无法确定
【思路点拨】直接根据点与圆的位置关系进行判断.
【答案】解:∵点P到圆心的距离为3cm,
而⊙O的半径为4cm,
∴点P到圆心的距离小于圆的半径,
∴点P在圆内,
故选:A.
【点睛】本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.
13.(2018秋?安庆期末)在平面直角坐标系中,⊙O的圆心在点(1,0),半径为2,则下面各点在⊙O上的是( )
A.(2,0) B.(0,2) C.(0,) D.(,0)
【思路点拨】根据点的坐标性质结合勾股定理得出斜边长,进而得出点与⊙O关系.
【答案】解:A、点(2,0)到⊙O的圆心(1,0)的距离为:2﹣1=1<2,所以点(2,0)在⊙O内,错误;
B、点(0,2)到⊙O的圆心(1,0)的距离为:>2,所以点(2,0)在⊙O外,错误;
C、点(0,)到⊙O的圆心(1,0)的距离为:=2,所以点(2,0)在⊙O上,正确;
D、点(,0)到⊙O的圆心(1,0)的距离为:﹣1<2,所以点(2,0)在⊙O内,错误;
故选:C.
【点睛】此题主要考查了点与圆的位置关系,点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点P在圆外d>r,②点P在圆上d=r,③点P在圆内d<r.
14.(2018秋?城厢区期末)在平面直角坐标系xOy中,若点P(4,3)在⊙O内,则⊙O的半径r的取值范围是( )
A.0<r<4 B.3<r<4 C.4<r<5 D.r>5
【思路点拨】本题可先由勾股定理等性质算出点与圆心的距离d,再根据点与圆心的距离与半径的大小关系,即当d>r时,点在圆外;当d=r时,点在圆上;点在圆外;当d<r时,点在圆内;来确定点与圆的位置关系.
【答案】解:∵点P(4,3),
∴PO==5,
∵点P在⊙O内,
∴r>OP,即r>5,
故选:D.
【点睛】本题主要考查点与圆的位置关系,解题的关键是能够根据勾股定理求得点到圆心的距离,根据数量关系判断点和圆的位置关系.
15.(2019?金山区一模)如图,在Rt△ABC中,∠C=90°,BC=2,∠B=60°,⊙A的半径为3,那么下列说法正确的是( )
A.点B、点C都在⊙A内 B.点C在⊙A内,点B在⊙A外
C.点B在⊙A内,点C在⊙A外 D.点B、点C都在⊙A外
【思路点拨】先解直角△ABC,求出AB、AC的长,再根据点到圆心距离与半径的关系可以确定点B、点C与⊙A的位置关系.
【答案】解:∵在Rt△ABC中,∠C=90°,BC=2,∠B=60°,
∴∠A=30°,
∴AB=2BC=4,AC=BC=2,
∵⊙A的半径为3,4>3,2>3,
∴点B、点C都在⊙A外.
故选:D.
【点睛】本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.也考查了含30°角的直角三角形的性质.
16.(2016秋?柯桥区校级月考)小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )
A.第一块 B.第二块 C.第三块 D.第四块
【思路点拨】要确定圆的大小需知道其半径.根据垂径定理知第①块可确定半径的大小.
【答案】解:第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
【点睛】本题考查了确定圆的条件,解题的关键是熟练掌握:圆上任意两弦的垂直平分线的交点即为该圆的圆心.
三.解答题
17.(2017秋?休宁县期中)如图,已知矩形ABCD的边AB=3cm,BC=4cm,以点A为圆心,4cm为半径作⊙A,则点B,C,D与⊙A怎样的位置关系.
【思路点拨】连接AC,根据勾股定理求出AC的长,进而得出点B,C,D与⊙A的位置关系.
【答案】解:连接AC
,
∵AB=3cm,BC=AD=4cm,
∴AC=5cm,
∴点B在⊙A内,点D在⊙A上,点C在⊙A外.
【点睛】此题主要考查了点与圆的位置关系,解决本题要注意点与圆的位置关系,要熟悉勾股定理,及点与圆的位置关系.
18.已知:如图,△ABC中,∠C=90°,AC=2cm,BC=4cm,CM是中线,以C为圆心,以cm长为半径画圆,则点A、B、M与⊙C的关系如何?
【思路点拨】点与圆的位置关系由三种情况:设点到圆心的距离为d,则当d=R时,点在圆上;当d>R时,点在圆外;当d<R时,点在圆内.
【答案】解:根据勾股定理,有AB==2(cm);
∵CA=2cm<cm,
∴点A在⊙O内,
∵BC=4cm>cm,
∴点B在⊙C外;
由中线定理得:CM=cm
∴M点在⊙C上.
【点睛】本题主要考查了点与圆的位置关系.
19.如图,在△ABC中,∠ABC=90°,AB=4cm,AC=6cm,AM是中线.
(1)以A为圆心,4cm长为半径作⊙A,则点B、C、M与⊙A是什么位置关系?
(2)若以A为圆心作⊙A,使点B、C、M三点中至少有一点在圆内,且至少有一点在圆外,则⊙A的半径r的取值范围是什么?
【思路点拨】(1)根据点与圆的位置关系判定方法,比较AB,AC,AM与AB的大小关系即可得出答案;
(2)利用分界点当B、C、M三点中至少有一点在⊙A内时,以及当至少有一点在⊙A外时,分别求出即可.
【答案】解:(1)∵AB=4cm=⊙A的半径,
∴点B在⊙A上;
∵AC=6cm>4cm,
∴点C在⊙A外;
由勾股定理,得BC==2cm,
∵AM是BC边上的中线,
∴AM=BC=cm<4cm,
∴点M在⊙A内;
(2)以点A为圆心作⊙A,使B、C、M三点中至少有一点在⊙A内时,r>cm,
当至少有一点在⊙A外时,r<6cm,
故⊙A的半径r的取值范围为:cm<r<6cm.
【点睛】此题主要考查了点与圆的位置关系
20.(2018秋?微山县期中)小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用勾股定理得到结论:P1P2=
;他还证明了线段P1P2的中点P(x,y)的坐标公式是:x=,y=;
启发应用
请利用上面的信息,解答下面的问题:
如图,在平面直角坐标系中,已知A(8,0),B(0,6),C(1,7),⊙M经过原点O及点A、B.
(1)求⊙M的半径及圆心M的坐标;
(2)判断点C与⊙M的位置关系,并说明理由.
【思路点拨】(1)先确定出AB=10,进而求出圆M的半径,最后用线段的中点坐标公式即可得出结论;
(2)求出CM=5和圆M的半径比较大小,即可得出结论.
【答案】解:(1)∵∠AOB=90°,
∴AB是⊙M的直径,
∵A(8,0),B(0,6),
∴AB==10,
∴⊙M的半径为5,
由线段中点坐标公式x=,y=,得x=4,y=3,
∴M(4,3),
(2)点C在⊙M上,
理由:∵C(1,7),M(4,3),
∴CM==5,
∴点C在⊙M上.
【点睛】本题主要考查了点与圆的位置关系,解题的关键是对两点间的距离公式的理解和掌握,灵活运用线段中点坐标公式和两点间距离公式.
21.如图,已知直线l和A,B两点,求作经过A,B两点的圆,使圆心在直线l上.
【思路点拨】连接AB,作出AB的垂直平分线交直线l于O点,以O为圆心,OA为半径作圆.
【答案】解:如图所示,⊙O即为所求.
【点睛】本题主要考查确定圆的条件的知识点,本题要求有较强的作图能力,对同学来说需要熟练掌握.
22.如图.已知点A(1,2)、B(4,1)、C(8,3).利用坐标网格和你的观察力.请直按说出△ABC外心的坐标和外接圆半径.
【思路点拨】作CD⊥AB于D,点O为外心,根据图形和坐标的性质得到AD和CD的长度,根据外心的概念和勾股定理列出方程,解方程得到答案.
【答案】解:分别作AB、BC的垂直平分线交于点P,
由图形可知,点P的坐标为:(4,6),
外接圆的半径为5.
答:△ABC外心的坐标为(4,6),外接圆半径为5.
【点睛】本题考查的是坐标与图形的性质、三角形的外心的性质和勾股定理的应用,正确根据坐标求出线段的长度、根据题意列出方程是解题的关键.
23.(2018秋?兴化市校级月考)如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)经过A、B、C三点的圆弧所在圆的圆心点M的坐标为 (2,0) ;
(2)判断点D(4,﹣3)与⊙M的位置关系.
【思路点拨】(1)根据垂径定理的推论:弦的垂直平分线必过圆心,可以作弦AB和BC的垂直平分线,交点即为圆心.
(2)求出⊙M的半径,MD的长即可判断;
【答案】解:(1)根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,0)
故答案为:2,0.
(2)圆的半径AM==2,
线段MD==<2,
所以点D在⊙M内.
【点睛】本题主要考查确定圆的条件和坐标与图形性质的知识点,点与圆的位置关系等知识,能够根据垂径定理的推论得到圆心的位置是解决问题的关键.
24.(2018?常德二模)如图,AB是半圆O的直径,D是半圆上的一点,∠DOB=75°,DC交BA的延长线于E,交半圆于C,且CE=AO,求∠E的度数.
【思路点拨】连结OC,如图,由CE=AO,OA=OC得到OC=EC,则根据等腰三角形的性质得∠E=∠1,再利用三角形外角性质得∠2=∠E+∠1=2∠E,加上∠D=∠2=2∠E,
所以∠BOD=∠E+∠D,即∠E+2∠E=75°,然后解方程即可.
【答案】解:连结OC,如图,
∵CE=AO,
而OA=OC,
∴OC=EC,
∴∠E=∠1,
∴∠2=∠E+∠1=2∠E,
∵OC=OD,
∴∠D=∠2=2∠E,
∵∠BOD=∠E+∠D,
∴∠E+2∠E=75°,
∴∠E=25°.
【点睛】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质.
25.我们将能完全覆盖三角形的最小圆称为该三角形的最小覆盖圆,求:能覆盖住边长为,,4的三角形的最小圆的半径.
【思路点拨】根据等腰三角形的三边长可知,此等腰三角形是锐角三角形,因此能盖住三角形的最小圆应该是三角形的外接圆;可过等腰三角形的顶角顶点作圆的直径,通过勾股定理和相交弦定理求出此圆的外接圆半径.
【答案】解:如图;△ABC中,AB=AC=,BC=4;
由于△ABC是锐角三角形,因此能覆盖此三角形的最小圆应该是△ABC的外接圆⊙O;
过A作⊙O的直径AE,交BC于D;
在Rt△ABD中,AB=,BD=2,
由勾股定理得:AD=3;
由相交弦定理知:BD2=AD?DE,即DE=BD2÷AD=;
故⊙O的半径最小为:(AD+DE)=×(3+)=.
【点睛】此题考查了等腰三角形的性质、勾股定理、垂径定理、相交弦定理等知识的综合应用,首先判断出△ABC的形状是解题的关键.
同课章节目录
