浙教版九年级数学上册《3.2 图形的旋转》同步练习(解析版)
文档属性
| 名称 | 浙教版九年级数学上册《3.2 图形的旋转》同步练习(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 337.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-17 00:00:00 | ||
图片预览


文档简介
3.2 图形的旋转
一.填空题
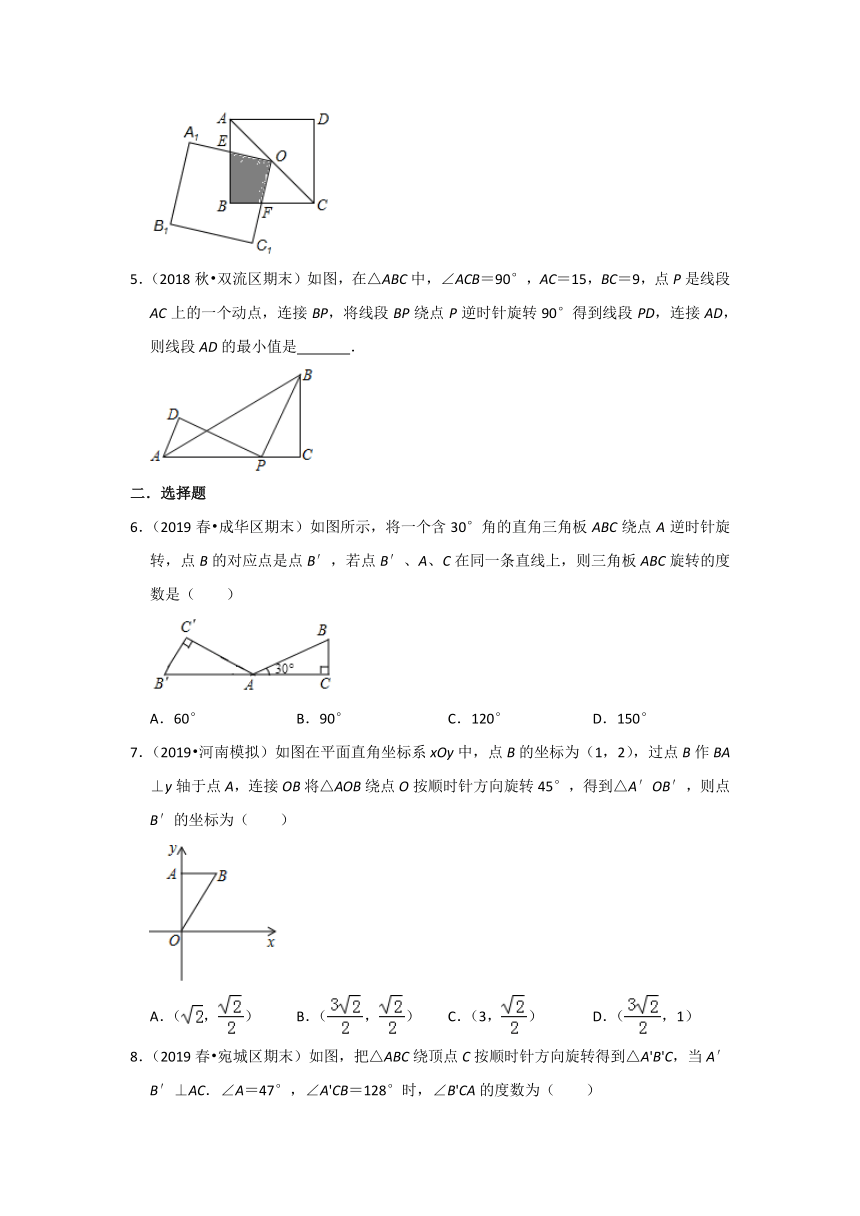
1.(2019春?高邮市期中)如图,在Rt△ABC中,∠ACB=90°,∠A=35°,将△ABC绕点C顺时针旋转,使点B落在AB边上的点D处,则∠ACD= .
2.(2019春?锦州期末)如图,将△ABC绕点A逆时针旋转140°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为 .
3.(2019春?海陵区校级月考)如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且∠DAG=60°,若EC=,则AB= .
4.(2019春?天津期末)如图,已知正方形ABCD,对角线AC的中点为O,点O同时是正方形A1B1C1O的一个顶点,A1O交AB于点E,C1O交BC于点F.若这两个正方形的边长都是3,将正方形A1B1C1O绕点O转动.
(1)两个正方形重叠部分的面积 改变(填“会”或“不会”).
(2)两个正方形重叠部分的面积若改变,说明理由;若不改变,直接写出重叠部分的面积.请将答案写在横线上 .
5.(2018秋?双流区期末)如图,在△ABC中,∠ACB=90°,AC=15,BC=9,点P是线段AC上的一个动点,连接BP,将线段BP绕点P逆时针旋转90°得到线段PD,连接AD,则线段AD的最小值是 .
二.选择题
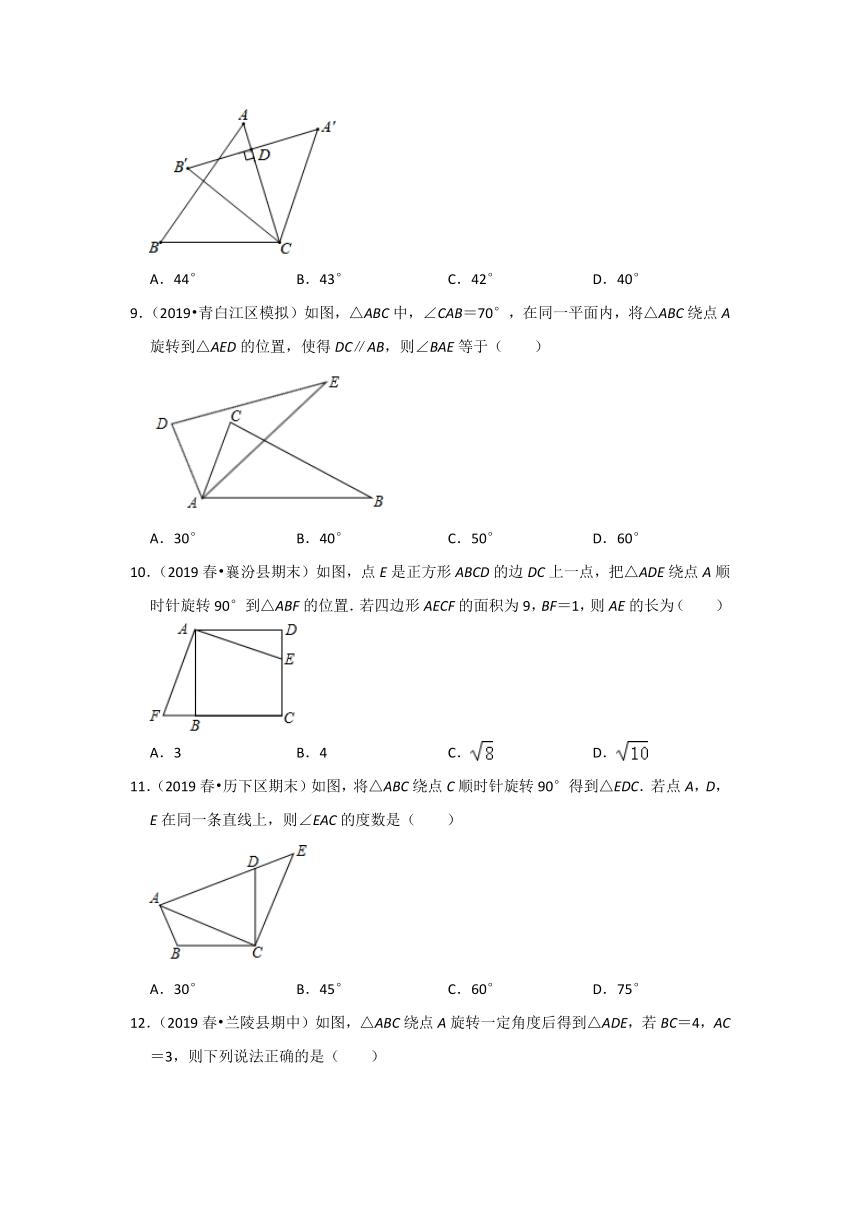
6.(2019春?成华区期末)如图所示,将一个含30°角的直角三角板ABC绕点A逆时针旋转,点B的对应点是点B′,若点B′、A、C在同一条直线上,则三角板ABC旋转的度数是( )
A.60° B.90° C.120° D.150°
7.(2019?河南模拟)如图在平面直角坐标系xOy中,点B的坐标为(1,2),过点B作BA⊥y轴于点A,连接OB将△AOB绕点O按顺时针方向旋转45°,得到△A′OB′,则点B′的坐标为( )
A.(,) B.(,) C.(3,) D.(,1)
8.(2019春?宛城区期末)如图,把△ABC绕顶点C按顺时针方向旋转得到△A'B'C,当A′B′⊥AC.∠A=47°,∠A'CB=128°时,∠B'CA的度数为( )
A.44° B.43° C.42° D.40°
9.(2019?青白江区模拟)如图,△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使得DC∥AB,则∠BAE等于( )
A.30° B.40° C.50° D.60°
10.(2019春?襄汾县期末)如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置.若四边形AECF的面积为9,BF=1,则AE的长为( )
A.3 B.4 C. D.
11.(2019春?历下区期末)如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,则∠EAC的度数是( )
A.30° B.45° C.60° D.75°
12.(2019春?兰陵县期中)如图,△ABC绕点A旋转一定角度后得到△ADE,若BC=4,AC=3,则下列说法正确的是( )
A.DE=3 B.AE=4
C.∠ACB是旋转角 D.∠CAE是旋转角
13.(2019春?南海区期末)如图,△ABC中,∠ACB=90°,∠ABC=22.5°,将△ABC绕着点C顺时针旋转,使得点A的对应点D落在边BC上,点B的对应点是点E,连接BE.下列说法中,正确的有( )
①DE⊥AB; ②∠BCE是旋转角; ③∠BED=30°;④△BDE与△CDE面积之比是:1.
A.1个 B.2个 C.3个 D.4个
14.(2019春?沙县期末)如图,在△ABC中,AB=3,AC=2,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC,则BC1的长为( )
A. B. C.4 D.6
15.(2019春?桂林期末)如图,正方形ABCD的对角线AC与BD相交于点O.将∠COB绕点O顺时针旋转,设旋转角为α(0<α<90°),角的两边分别与BC,AB交于点M,N,连接DM,CN,MN,下列四个结论:
①∠CDM=∠COM;②CN⊥DM;③△CNB≌△DMC;④AN2+CM2=MN2;其中正确结论的个数是( )
A.1 B.2 C.3 D.4
三.解答题
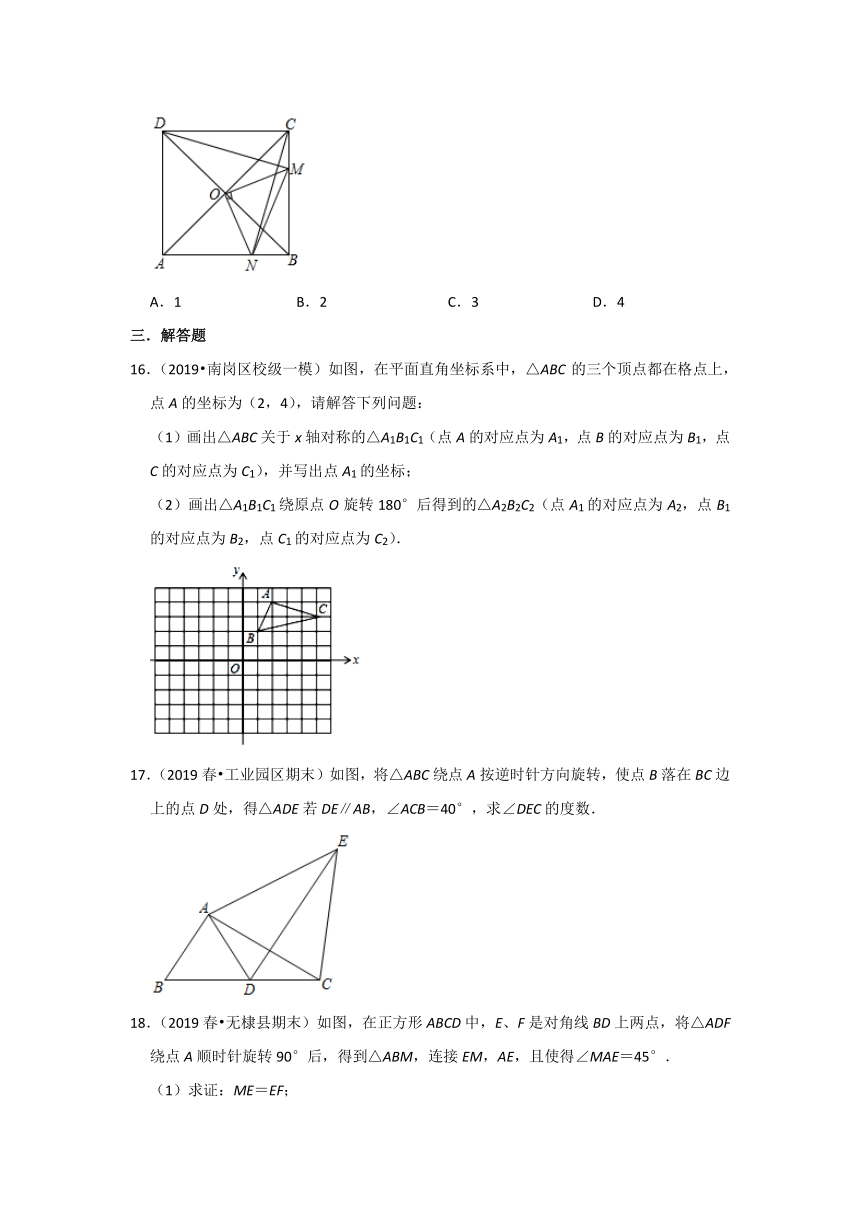
16.(2019?南岗区校级一模)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1(点A的对应点为A1,点B的对应点为B1,点C的对应点为C1),并写出点A1的坐标;
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2(点A1的对应点为A2,点B1的对应点为B2,点C1的对应点为C2).
17.(2019春?工业园区期末)如图,将△ABC绕点A按逆时针方向旋转,使点B落在BC边上的点D处,得△ADE若DE∥AB,∠ACB=40°,求∠DEC的度数.
18.(2019春?无棣县期末)如图,在正方形ABCD中,E、F是对角线BD上两点,将△ADF绕点A顺时针旋转90°后,得到△ABM,连接EM,AE,且使得∠MAE=45°.
(1)求证:ME=EF;
(2)求证:EF2=BE2+DF2.
19.(2019?道里区三模)如图,在△ABC中,AC=AB,把△ABC绕点A顺时针旋转得到△ADE(点B、C分别对应点D、E),BD和CE交于点F.
(1)求证:CE=BD;
(2)若AB=2,∠BAC=45°,当四边形ADFC是平行四边形时,求BF的长.
20.(2019春?商河县期中)如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°.若固定△ABC,将△DEC绕点C旋转.
(1)当△DEC统点C旋转到点D恰好落在AB边上时,如图2.
①当∠B=∠E=30°时,此时旋转角的大小为 ;
②当∠B=∠E=α时,此时旋转角的大小为 (用含α的式子表示).
(2)当△DEC绕点C旋转到如图3所示的位置时,小杨同学猜想:△BDC的面积与△AEC的面积相等,试判断小杨同学的猜想是否正确,若正确,请你证明小杨同学的猜想.若不正确,请说明理由.
参考答案
一.填空题
1.(2019春?高邮市期中)如图,在Rt△ABC中,∠ACB=90°,∠A=35°,将△ABC绕点C顺时针旋转,使点B落在AB边上的点D处,则∠ACD= 20° .
【思路点拨】由旋转的性质可得CD=CB,可得∠B=∠CDB=55°,由三角形的外角的性质可求∠ACD的度数.
【答案】解:∵∠ACB=90°,∠A=35°,
∴∠B=55°,
∵将△ABC绕点C顺时针旋转,使点B落在AB边上的点D处,
∴CD=CB
∴∠B=∠CDB=55°,
∵∠CDB=∠A+∠ACD
∴∠ACD=55°﹣35°=20°
故答案为:20°
【点睛】本题是旋转的性质,等腰三角形的性质,熟练运用旋转的性质是本题的关键.
2.(2019春?锦州期末)如图,将△ABC绕点A逆时针旋转140°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为 20° .
【思路点拨】由旋转的性质可得AB=AD,∠BAD=140°,由等腰三角形的性质可求∠B的度数.
【答案】解:∵将△ABC绕点A逆时针旋转140°,得到△ADE,
∴AB=AD,∠BAD=140°
∴∠B=20°
故答案为:20°
【点睛】本题考查了旋转的性质,熟练运用旋转的性质是本题的关键.
3.(2019春?海陵区校级月考)如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且∠DAG=60°,若EC=,则AB= 2 .
【思路点拨】根据旋转的性质可知AB=AE=DC=x,则在Rt△ADE中,根据30°直角三角形的性质可知AE=2DE,构造关于x的方程即可.
【答案】解:∵将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,
∴AE=AB.
设AB=x,则CD=AE=x,DE=x﹣,
∵∠DAG=60°,∠GAE=90°,
∴∠DAE=30°,
在Rt△ADE中,AE=2DE,
∴x=2(x﹣),解得x=2.
故答案为2.
【点睛】此题考查了旋转的性质,矩形的性质,熟练掌握旋转的性质是解本题的关键.
4.(2019春?天津期末)如图,已知正方形ABCD,对角线AC的中点为O,点O同时是正方形A1B1C1O的一个顶点,A1O交AB于点E,C1O交BC于点F.若这两个正方形的边长都是3,将正方形A1B1C1O绕点O转动.
(1)两个正方形重叠部分的面积 不会 改变(填“会”或“不会”).
(2)两个正方形重叠部分的面积若改变,说明理由;若不改变,直接写出重叠部分的面积.请将答案写在横线上 .
【思路点拨】(1)由“ASA”可证△AOE≌△BOF,可得S△AOE=S△BOF,即可求解;
(2)求出正方形的面积,即可求解.
【答案】解:(1)连接BO,
在正方形ABCD中,AO=BO,∠AOB=90°,∠OAB=∠OBC=45°,
∵∠AOE+∠EOB=90°,∠BOF+∠EOB=90°,
∴∠AOE=∠BOF,且OA=OB,∠OAE=∠OBF=45°
∴△AOE≌△BOF(ASA).
∴S△AOE=S△BOF,
∴S四边形OEBF=S△EOB+S△OBF=S△EOB+S△AOE=S△AOB=S正方形ABCD,
故答案为:不会
(2)∵两个正方形的边长都是3,
∴重叠部分的面积=×9=
故答案为:
【点睛】本题考查了旋转的性质,正方形的性质,全等三角形的判定和性质,证明△AOE≌△BOF是本题的关键.
5.(2018秋?双流区期末)如图,在△ABC中,∠ACB=90°,AC=15,BC=9,点P是线段AC上的一个动点,连接BP,将线段BP绕点P逆时针旋转90°得到线段PD,连接AD,则线段AD的最小值是 3 .
【思路点拨】如图,过点D作DE⊥AC于E,有旋转的性质可得DP=BP,∠DPB=90°,由“AAS”可证△DEP≌△PCB,可得DE=CP,EP=BC=9,可求AE+DE=6,由勾股定理和二次函数的性质可求解.
【答案】解:如图,过点D作DE⊥AC于E,
∵将线段BP绕点P逆时针旋转90°得到线段PD,
∴DP=BP,∠DPB=90°,
∴∠DPE+∠BPC=90°,且∠BPC+∠PBC=90°,
∴∠DPE=∠PBC,且DP=BP,∠DEP=∠C=90°,
∴△DEP≌△PCB(AAS)
∴DE=CP,EP=BC=9,
∵AE+PC=AC﹣EP=6
∴AE+DE=6,
∵AD2=AE2+DE2,
∴AD2=AE2+(6﹣AE)2,
∴AD2=2(AE﹣3)2+18,
当AE=3时,AD有最小值为3,
故答案为3
【点睛】本题考查了旋转的性质,全等三角形的判定和性质,勾股定理,利用二次函数的性质求最小值是本题的关键.
二.选择题
6.(2019春?成华区期末)如图所示,将一个含30°角的直角三角板ABC绕点A逆时针旋转,点B的对应点是点B′,若点B′、A、C在同一条直线上,则三角板ABC旋转的度数是( )
A.60° B.90° C.120° D.150°
【思路点拨】根据旋转角的定义,两对应边的夹角就是旋转角,即可求解.
【答案】解:旋转角是∠BAB′=180°﹣30°=150°.
故选:D.
【点睛】本题考查的是旋转的性质,掌握对应点与旋转中心所连线段的夹角等于旋转角是解题的关键.
7.(2019?河南模拟)如图在平面直角坐标系xOy中,点B的坐标为(1,2),过点B作BA⊥y轴于点A,连接OB将△AOB绕点O按顺时针方向旋转45°,得到△A′OB′,则点B′的坐标为( )
A.(,) B.(,) C.(3,) D.(,1)
【思路点拨】将线段OB绕点O顺时针旋转90°得到OE.连接BE交OB′于F,作FH⊥x轴于H,B′G⊥x轴于G.首先确定点F的坐标,再利用平行线分线段成比例定理解决问题即可.
【答案】解:将线段OB绕点O顺时针旋转90°得到OE.连接BE交OB′于F,作FH⊥x轴于H,B′G⊥x轴于G.
∵B(1,2),可得E(2,﹣1),
∵∠BOF=∠EOF,OB=OE,
∴BF=EF,
∴F(,),
∴OF==,OB=OB′==,
∵FH∥B′G,
∴==,
∴==,
∴OG=,B′G=,
∴B′(,)
故选:B.
【点睛】本题考查坐标与图形变化﹣旋转,等腰三角形的性质,平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,构造特殊三角形解决问题,属于中考常考题型.
8.(2019春?宛城区期末)如图,把△ABC绕顶点C按顺时针方向旋转得到△A'B'C,当A′B′⊥AC.∠A=47°,∠A'CB=128°时,∠B'CA的度数为( )
A.44° B.43° C.42° D.40°
【思路点拨】根据旋转的性质可知∠A′=∠A=47°,则∠A′CA=90°﹣47°=43°,由∠BCB′=∠A′CA=43°,则∠B′CA=∠A′CB﹣∠A′CA﹣∠BCB′可求.
【答案】解:根据旋转的性质可知∠A′=∠A=47°,
∴∠A′CA=90°﹣47°=43°.
根据旋转的性质可知旋转角相等,即∠BCB′=∠A′CA=43°,
∴∠B′CA=∠A′CB﹣∠A′CA﹣∠BCB′=128°﹣43°﹣43°=42°.
故选:C.
【点睛】本题主要考查了旋转的性质,解决这类问题要找准旋转角、以及旋转后对应的线段和角.
9.(2019?青白江区模拟)如图,△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使得DC∥AB,则∠BAE等于( )
A.30° B.40° C.50° D.60°
【思路点拨】由旋转的性质可得AD=AC,∠DAC=∠EAB,由等腰三角形的性质和三角形的内角和定理可求解.
【答案】解:如图,
∵DC∥AB,
∴∠DCA=∠CAB=70°,
∵将△ABC绕点A旋转到△AED的位置,
∴AD=AC,∠DAC=∠EAB,
∴∠ADC=∠DCA=70°
∴∠DAC=∠EAB=40°
故选:B.
【点睛】本题考查了旋转的性质,平行线的性质,熟练运用旋转的旋转是本题的关键.
10.(2019春?襄汾县期末)如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置.若四边形AECF的面积为9,BF=1,则AE的长为( )
A.3 B.4 C. D.
【思路点拨】由旋转的性质可得BF=DE=1,S△AFB=S△ADE,可求AD=3,由勾股定理可求AE的长.
【答案】解:∵把△ADE绕点A顺时针旋转90°到△ABF的位置
∴BF=DE=1,S△AFB=S△ADE,
∴S正方形ABCD=S四边形AECF=9
∴AD=3
∴AE==
故选:D.
【点睛】本题考查了旋转的性质,正方形的性质,求出AD的长是本题的关键.
11.(2019春?历下区期末)如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,则∠EAC的度数是( )
A.30° B.45° C.60° D.75°
【思路点拨】用性质的性质可知△ACE是等腰直角三角形,由此即可解决问题.
【答案】解:由题意:A,D,E共线,
又∵CA=CE,∠ACE=90°,
∴∠EAC=∠E=45°,
故选:B.
【点睛】本题考查旋转变换,等腰直角三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题.
12.(2019春?兰陵县期中)如图,△ABC绕点A旋转一定角度后得到△ADE,若BC=4,AC=3,则下列说法正确的是( )
A.DE=3 B.AE=4
C.∠ACB是旋转角 D.∠CAE是旋转角
【思路点拨】由旋转的意义可得,将△ABC绕点A逆时针旋转一个角度后得到△ADE,此时对应边为;AC=AE,AB=AD,CB=ED,旋转角为∠CAE或∠BAD,以此逐个进行判断,得出答案.
【答案】解:由旋转的性质得:DE=BC=4,故A不正确;AE=AC=3,故B不正确;旋转角是∠CAE,故D正确;∠ACB不是旋转角,故C不正确;
故选:D.
【点睛】考查旋转的性质,对应边相等、对应角相等,理解旋转角的意义等知识,掌握这些知识是前提和基础.
13.(2019春?南海区期末)如图,△ABC中,∠ACB=90°,∠ABC=22.5°,将△ABC绕着点C顺时针旋转,使得点A的对应点D落在边BC上,点B的对应点是点E,连接BE.下列说法中,正确的有( )
①DE⊥AB; ②∠BCE是旋转角; ③∠BED=30°;④△BDE与△CDE面积之比是:1.
A.1个 B.2个 C.3个 D.4个
【思路点拨】由旋转的性质可得AC=DC,BC=CE,∠ABC=∠CED=22.5°,∠BCE是旋转角,可判断①②,由等腰三角形的性质可判断③④.
【答案】解:如图,连接AD,延长ED交AB于点F,
∵将△ABC绕着点C顺时针旋转,使得点A的对应点D落在边BC上,
∴AC=DC,BC=CE,∠ABC=∠CED=22.5°,∠BCE是旋转角,
∵∠ABC+∠BAC=90°,
∴∠BAC+∠CED=90°
∴∠AFE=90°
∴DE⊥AB,
故①②正确
∵∠BCE=90°,BC=CE
∴∠BEC=45°
∴∠BED=∠BEC﹣∠CED=22.5°
故③错误
∵AC=CD,
∴AD=CD,∠DAC=∠ADC=45°
∵∠ADC=∠ABC+∠BAD
∴∠ABC=∠BAD=22.5°
∴AD=BD=CD
∴△BDE与△CDE面积之比是:1.
故④正确
故选:C.
【点睛】本题考查了旋转的性质,等腰三角形的性质,熟练运用旋转的性质是本题的关键.
14.(2019春?沙县期末)如图,在△ABC中,AB=3,AC=2,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC,则BC1的长为( )
A. B. C.4 D.6
【思路点拨】根据旋转的性质得出AC=AC1,∠BAC1=90°,进而利用勾股定理解答即可.
【答案】解:∵将△ABC绕点A逆时针旋转60°得到△AB1C1,
∴AC=AC1=2,∠CAC1=60°,
∵AB=3,AC=2,∠BAC=30°,
∴∠BAC1=90°,
∴在Rt△BAC1中,BC1==.
故选:B.
【点睛】此题考查旋转的性质,解题时注意:对应点到旋转中心的距离相等,对应点与旋转中心所连线段的夹角等于旋转角.
15.(2019春?桂林期末)如图,正方形ABCD的对角线AC与BD相交于点O.将∠COB绕点O顺时针旋转,设旋转角为α(0<α<90°),角的两边分别与BC,AB交于点M,N,连接DM,CN,MN,下列四个结论:
①∠CDM=∠COM;②CN⊥DM;③△CNB≌△DMC;④AN2+CM2=MN2;其中正确结论的个数是( )
A.1 B.2 C.3 D.4
【思路点拨】由“ASA”可证△OCM≌△OBN,可得CM=BN,∠CDM=∠BCN,由余角的性质可判断②,由点O,点M,点B,点N四点共圆可判断①,由“SAS”可证△DCM≌△CNB,由勾股定理可判断④.
【答案】解:∵四边形ABCD是正方形
∴CD=BC,BO=CO,AC⊥BD,∠ACB=∠ABD=45°
∵将∠COB绕点O顺时针旋转,
∴∠COM=∠BON,且BO=CO,∠ACB=∠ABD
∴△OCM≌△OBN(ASA)
∴CM=BN,∠CDM=∠BCN
∵∠CDM+∠CMD=90°
∴∠BCN+∠CMD=90°
∴CN⊥DM
故②正确
∵∠MON=∠ABC=90°
∴点O,点M,点B,点N四点共圆
∴∠BON=∠BMN=∠COM>∠BCN=∠CDM
故①错误
∵CM=BN,CD=BC,∠ABC=∠DCB=90°
∴△DCM≌△CNB(SAS)
故③正确
∵AB=BC,BN=CM
∴AN=BM
∵BN2+BM2=MN2,
∴AN2+CM2=MN2;
故④正确
故选:C.
【点睛】本题主要考查了旋转的性质,正方形的性质、全等三角形的判定与性质,勾股定理的综合应用,熟练掌握正方形的性质,证明三角形全等是解题的关键.
三.解答题
16.(2019?南岗区校级一模)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1(点A的对应点为A1,点B的对应点为B1,点C的对应点为C1),并写出点A1的坐标;
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2(点A1的对应点为A2,点B1的对应点为B2,点C1的对应点为C2).
【思路点拨】(1)分别作出A,B,C的对应点A1,B1,C1即可.
(2)分别作出点A1,B1,C1的对应点A2,B2,C2即可.
【答案】解:(1)△ABC关于x轴对称的△A1B1C1如图所示.
(2)△A2B2C2即为所求.
【点睛】本题考查作图﹣旋转变换,轴对称等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
17.(2019春?工业园区期末)如图,将△ABC绕点A按逆时针方向旋转,使点B落在BC边上的点D处,得△ADE若DE∥AB,∠ACB=40°,求∠DEC的度数.
【思路点拨】根据旋转的性质得到∠ADE=∠B,AB=AD,AC=AE,∠AED=∠ACD=40°,根据平行线的性质得到∠ADE=∠BAD,推出△ABD是等边三角形,△ACE是等边三角形,于是得到结论.
【答案】解:∵将△ABC绕点A按逆时针方向旋转得△ADE,
∴∠ADE=∠B,AB=AD,AC=AE,∠AED=∠ACD=40°,
∵DE∥AB,
∴∠ADE=∠BAD,
∴∠B=∠BAD,
∴BD=AD=AB,
∴△ABD是等边三角形,
∴∠BAD=60°,
∴∠CAE=60°,
∴△ACE是等边三角形,
∴∠AEC=60°,
∴∠DEC=60°﹣40°=20°.
【点睛】本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.
18.(2019春?无棣县期末)如图,在正方形ABCD中,E、F是对角线BD上两点,将△ADF绕点A顺时针旋转90°后,得到△ABM,连接EM,AE,且使得∠MAE=45°.
(1)求证:ME=EF;
(2)求证:EF2=BE2+DF2.
【思路点拨】(1)直接利用旋转的性质得出△AME≌△AFE(SAS),进而得出∠AEM=∠AEF,即可得出答案;
(2)利用(1)中所求,再结合勾股定理得出答案.
【答案】证明:(1)∵将△ADF绕点A顺时针旋转90°后,得到△ABM,
∴MB=DF,AM=AF,∠BAM=∠DAF,
∵∠EAM=45°,∠MAF=90°
∴∠FAE=45°,
∴∠MAE=∠FAE,
在△AME和△AFE中
,
∴△AME≌△AFE(SAS)
ME=EF.
(2)由(1)得△AME≌△AFE,
∴ME=EF,
∵∠ABM=∠ADF=45°,∠ABD=45°,
∴∠MBE=90°.
在Rt△MBE中,∵MB2+BE2=ME2,
又∵MB=DF,
∴EF2=BE2+DF2.
【点睛】此题主要考查了旋转的性质以及全等三角形的判定与性质和勾股定理等知识,正确得出△AQE≌△AFE(SAS)是解题关键.
19.(2019?道里区三模)如图,在△ABC中,AC=AB,把△ABC绕点A顺时针旋转得到△ADE(点B、C分别对应点D、E),BD和CE交于点F.
(1)求证:CE=BD;
(2)若AB=2,∠BAC=45°,当四边形ADFC是平行四边形时,求BF的长.
【思路点拨】(1)由旋转的性质可得AD=AB,AE=AC,∠DAE=∠BAC,由“SAS”可证△AEC≌△ADB,可得CE=BD;
(2)由平行四边形的性质可得DF=AC,AC∥BD,可得∠ABD=∠BAC=45°,可求∠BAD=90°,可得BD=AB=2,即可求BF的长.
【答案】证明:(1)∵把△ABC绕点A顺时针旋转得到△ADE
∴△ABC≌△ADE
∴AD=AB,AE=AC,∠DAE=∠BAC
∴∠DAE+∠BAE=∠BAC+∠BAE
∴∠DAB=∠EAC,
∵AB=AC
∴AD=AB=AC=AE
∵∠DAB=∠EAC,AD=AB,AC=AE
∴△AEC≌△ADB(SAS)
∴CE=BD
(2)∵四边形ADFC是平行四边形
∴DF=AC,AC∥BD
∴∠ABD=∠BAC=45°
∵AB=AD
∴∠DBA=∠BDA=45°
∴∠BAD=90°
∴BD=AB=2
∵DF=AC=AB=2
∴BF=BD﹣DF=2﹣2
【点睛】本题考查了旋转的性质,平行四边形的性质,全等三角形的判定和性质,熟练运用旋转的性质是本题的关键.
20.(2019春?商河县期中)如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°.若固定△ABC,将△DEC绕点C旋转.
(1)当△DEC统点C旋转到点D恰好落在AB边上时,如图2.
①当∠B=∠E=30°时,此时旋转角的大小为 60° ;
②当∠B=∠E=α时,此时旋转角的大小为 2α (用含α的式子表示).
(2)当△DEC绕点C旋转到如图3所示的位置时,小杨同学猜想:△BDC的面积与△AEC的面积相等,试判断小杨同学的猜想是否正确,若正确,请你证明小杨同学的猜想.若不正确,请说明理由.
【思路点拨】(1)①证明△ADC是等边三角形即可.
②如图2中,作CH⊥AD于H.想办法证明∠ACD=2∠B即可解决问题.
(2)小扬同学猜想是正确的.过B作BN⊥CD于N,过E作EM⊥AC于M,如图3,想办法证明△CBN≌△CEM(AAS)即可解决问题.
【答案】解:(1)①∵∠B=30°,∠ACB=90°,
∴∠CAD=90°﹣30°=60°,
∵CA=CD,
∴△ACD是等边三角形,
∴∠ACD=60°,
∴旋转角为60°,
故答案为60°.
②如图2中,作CH⊥AD于H.
∵CA=CD,CH⊥AD,
∴∠ACH=∠DCH,
∵∠ACH+∠CAB=90°,∠CAB+∠B=90°,
∴∠ACH=∠B,
∴∠ACD=2∠ACH=2∠B=2α,
∴旋转角为2α.
故答案为2α.
(2)小扬同学猜想是正确的,证明如下:
过B作BN⊥CD于N,过E作EM⊥AC于M,如图3,
∵∠ACB=∠DCE=90°,
∴∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3,
∵BN⊥CD于N,EM⊥AC于M,
∴∠BNC=∠EMC=90°,
∵△ACB≌△DCE,
∴BC=EC,
在△CBN和△CEM中,
∠BNC=∠EMC,∠1=∠3,BC=EC,
∴△CBN≌△CEM(AAS),
∴BN=EM,
∵S△BDC=?CD?BN,S△ACE=?AC?EM,
∵CD=AC,
∴S△BDC=S△ACE.
【点睛】本题考查旋转变换,全等三角形的判定和性质,等边三角形的判定和性质,等腰三角形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
一.填空题
1.(2019春?高邮市期中)如图,在Rt△ABC中,∠ACB=90°,∠A=35°,将△ABC绕点C顺时针旋转,使点B落在AB边上的点D处,则∠ACD= .
2.(2019春?锦州期末)如图,将△ABC绕点A逆时针旋转140°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为 .
3.(2019春?海陵区校级月考)如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且∠DAG=60°,若EC=,则AB= .
4.(2019春?天津期末)如图,已知正方形ABCD,对角线AC的中点为O,点O同时是正方形A1B1C1O的一个顶点,A1O交AB于点E,C1O交BC于点F.若这两个正方形的边长都是3,将正方形A1B1C1O绕点O转动.
(1)两个正方形重叠部分的面积 改变(填“会”或“不会”).
(2)两个正方形重叠部分的面积若改变,说明理由;若不改变,直接写出重叠部分的面积.请将答案写在横线上 .
5.(2018秋?双流区期末)如图,在△ABC中,∠ACB=90°,AC=15,BC=9,点P是线段AC上的一个动点,连接BP,将线段BP绕点P逆时针旋转90°得到线段PD,连接AD,则线段AD的最小值是 .
二.选择题
6.(2019春?成华区期末)如图所示,将一个含30°角的直角三角板ABC绕点A逆时针旋转,点B的对应点是点B′,若点B′、A、C在同一条直线上,则三角板ABC旋转的度数是( )
A.60° B.90° C.120° D.150°
7.(2019?河南模拟)如图在平面直角坐标系xOy中,点B的坐标为(1,2),过点B作BA⊥y轴于点A,连接OB将△AOB绕点O按顺时针方向旋转45°,得到△A′OB′,则点B′的坐标为( )
A.(,) B.(,) C.(3,) D.(,1)
8.(2019春?宛城区期末)如图,把△ABC绕顶点C按顺时针方向旋转得到△A'B'C,当A′B′⊥AC.∠A=47°,∠A'CB=128°时,∠B'CA的度数为( )
A.44° B.43° C.42° D.40°
9.(2019?青白江区模拟)如图,△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使得DC∥AB,则∠BAE等于( )
A.30° B.40° C.50° D.60°
10.(2019春?襄汾县期末)如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置.若四边形AECF的面积为9,BF=1,则AE的长为( )
A.3 B.4 C. D.
11.(2019春?历下区期末)如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,则∠EAC的度数是( )
A.30° B.45° C.60° D.75°
12.(2019春?兰陵县期中)如图,△ABC绕点A旋转一定角度后得到△ADE,若BC=4,AC=3,则下列说法正确的是( )
A.DE=3 B.AE=4
C.∠ACB是旋转角 D.∠CAE是旋转角
13.(2019春?南海区期末)如图,△ABC中,∠ACB=90°,∠ABC=22.5°,将△ABC绕着点C顺时针旋转,使得点A的对应点D落在边BC上,点B的对应点是点E,连接BE.下列说法中,正确的有( )
①DE⊥AB; ②∠BCE是旋转角; ③∠BED=30°;④△BDE与△CDE面积之比是:1.
A.1个 B.2个 C.3个 D.4个
14.(2019春?沙县期末)如图,在△ABC中,AB=3,AC=2,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC,则BC1的长为( )
A. B. C.4 D.6
15.(2019春?桂林期末)如图,正方形ABCD的对角线AC与BD相交于点O.将∠COB绕点O顺时针旋转,设旋转角为α(0<α<90°),角的两边分别与BC,AB交于点M,N,连接DM,CN,MN,下列四个结论:
①∠CDM=∠COM;②CN⊥DM;③△CNB≌△DMC;④AN2+CM2=MN2;其中正确结论的个数是( )
A.1 B.2 C.3 D.4
三.解答题
16.(2019?南岗区校级一模)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1(点A的对应点为A1,点B的对应点为B1,点C的对应点为C1),并写出点A1的坐标;
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2(点A1的对应点为A2,点B1的对应点为B2,点C1的对应点为C2).
17.(2019春?工业园区期末)如图,将△ABC绕点A按逆时针方向旋转,使点B落在BC边上的点D处,得△ADE若DE∥AB,∠ACB=40°,求∠DEC的度数.
18.(2019春?无棣县期末)如图,在正方形ABCD中,E、F是对角线BD上两点,将△ADF绕点A顺时针旋转90°后,得到△ABM,连接EM,AE,且使得∠MAE=45°.
(1)求证:ME=EF;
(2)求证:EF2=BE2+DF2.
19.(2019?道里区三模)如图,在△ABC中,AC=AB,把△ABC绕点A顺时针旋转得到△ADE(点B、C分别对应点D、E),BD和CE交于点F.
(1)求证:CE=BD;
(2)若AB=2,∠BAC=45°,当四边形ADFC是平行四边形时,求BF的长.
20.(2019春?商河县期中)如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°.若固定△ABC,将△DEC绕点C旋转.
(1)当△DEC统点C旋转到点D恰好落在AB边上时,如图2.
①当∠B=∠E=30°时,此时旋转角的大小为 ;
②当∠B=∠E=α时,此时旋转角的大小为 (用含α的式子表示).
(2)当△DEC绕点C旋转到如图3所示的位置时,小杨同学猜想:△BDC的面积与△AEC的面积相等,试判断小杨同学的猜想是否正确,若正确,请你证明小杨同学的猜想.若不正确,请说明理由.
参考答案
一.填空题
1.(2019春?高邮市期中)如图,在Rt△ABC中,∠ACB=90°,∠A=35°,将△ABC绕点C顺时针旋转,使点B落在AB边上的点D处,则∠ACD= 20° .
【思路点拨】由旋转的性质可得CD=CB,可得∠B=∠CDB=55°,由三角形的外角的性质可求∠ACD的度数.
【答案】解:∵∠ACB=90°,∠A=35°,
∴∠B=55°,
∵将△ABC绕点C顺时针旋转,使点B落在AB边上的点D处,
∴CD=CB
∴∠B=∠CDB=55°,
∵∠CDB=∠A+∠ACD
∴∠ACD=55°﹣35°=20°
故答案为:20°
【点睛】本题是旋转的性质,等腰三角形的性质,熟练运用旋转的性质是本题的关键.
2.(2019春?锦州期末)如图,将△ABC绕点A逆时针旋转140°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为 20° .
【思路点拨】由旋转的性质可得AB=AD,∠BAD=140°,由等腰三角形的性质可求∠B的度数.
【答案】解:∵将△ABC绕点A逆时针旋转140°,得到△ADE,
∴AB=AD,∠BAD=140°
∴∠B=20°
故答案为:20°
【点睛】本题考查了旋转的性质,熟练运用旋转的性质是本题的关键.
3.(2019春?海陵区校级月考)如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且∠DAG=60°,若EC=,则AB= 2 .
【思路点拨】根据旋转的性质可知AB=AE=DC=x,则在Rt△ADE中,根据30°直角三角形的性质可知AE=2DE,构造关于x的方程即可.
【答案】解:∵将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,
∴AE=AB.
设AB=x,则CD=AE=x,DE=x﹣,
∵∠DAG=60°,∠GAE=90°,
∴∠DAE=30°,
在Rt△ADE中,AE=2DE,
∴x=2(x﹣),解得x=2.
故答案为2.
【点睛】此题考查了旋转的性质,矩形的性质,熟练掌握旋转的性质是解本题的关键.
4.(2019春?天津期末)如图,已知正方形ABCD,对角线AC的中点为O,点O同时是正方形A1B1C1O的一个顶点,A1O交AB于点E,C1O交BC于点F.若这两个正方形的边长都是3,将正方形A1B1C1O绕点O转动.
(1)两个正方形重叠部分的面积 不会 改变(填“会”或“不会”).
(2)两个正方形重叠部分的面积若改变,说明理由;若不改变,直接写出重叠部分的面积.请将答案写在横线上 .
【思路点拨】(1)由“ASA”可证△AOE≌△BOF,可得S△AOE=S△BOF,即可求解;
(2)求出正方形的面积,即可求解.
【答案】解:(1)连接BO,
在正方形ABCD中,AO=BO,∠AOB=90°,∠OAB=∠OBC=45°,
∵∠AOE+∠EOB=90°,∠BOF+∠EOB=90°,
∴∠AOE=∠BOF,且OA=OB,∠OAE=∠OBF=45°
∴△AOE≌△BOF(ASA).
∴S△AOE=S△BOF,
∴S四边形OEBF=S△EOB+S△OBF=S△EOB+S△AOE=S△AOB=S正方形ABCD,
故答案为:不会
(2)∵两个正方形的边长都是3,
∴重叠部分的面积=×9=
故答案为:
【点睛】本题考查了旋转的性质,正方形的性质,全等三角形的判定和性质,证明△AOE≌△BOF是本题的关键.
5.(2018秋?双流区期末)如图,在△ABC中,∠ACB=90°,AC=15,BC=9,点P是线段AC上的一个动点,连接BP,将线段BP绕点P逆时针旋转90°得到线段PD,连接AD,则线段AD的最小值是 3 .
【思路点拨】如图,过点D作DE⊥AC于E,有旋转的性质可得DP=BP,∠DPB=90°,由“AAS”可证△DEP≌△PCB,可得DE=CP,EP=BC=9,可求AE+DE=6,由勾股定理和二次函数的性质可求解.
【答案】解:如图,过点D作DE⊥AC于E,
∵将线段BP绕点P逆时针旋转90°得到线段PD,
∴DP=BP,∠DPB=90°,
∴∠DPE+∠BPC=90°,且∠BPC+∠PBC=90°,
∴∠DPE=∠PBC,且DP=BP,∠DEP=∠C=90°,
∴△DEP≌△PCB(AAS)
∴DE=CP,EP=BC=9,
∵AE+PC=AC﹣EP=6
∴AE+DE=6,
∵AD2=AE2+DE2,
∴AD2=AE2+(6﹣AE)2,
∴AD2=2(AE﹣3)2+18,
当AE=3时,AD有最小值为3,
故答案为3
【点睛】本题考查了旋转的性质,全等三角形的判定和性质,勾股定理,利用二次函数的性质求最小值是本题的关键.
二.选择题
6.(2019春?成华区期末)如图所示,将一个含30°角的直角三角板ABC绕点A逆时针旋转,点B的对应点是点B′,若点B′、A、C在同一条直线上,则三角板ABC旋转的度数是( )
A.60° B.90° C.120° D.150°
【思路点拨】根据旋转角的定义,两对应边的夹角就是旋转角,即可求解.
【答案】解:旋转角是∠BAB′=180°﹣30°=150°.
故选:D.
【点睛】本题考查的是旋转的性质,掌握对应点与旋转中心所连线段的夹角等于旋转角是解题的关键.
7.(2019?河南模拟)如图在平面直角坐标系xOy中,点B的坐标为(1,2),过点B作BA⊥y轴于点A,连接OB将△AOB绕点O按顺时针方向旋转45°,得到△A′OB′,则点B′的坐标为( )
A.(,) B.(,) C.(3,) D.(,1)
【思路点拨】将线段OB绕点O顺时针旋转90°得到OE.连接BE交OB′于F,作FH⊥x轴于H,B′G⊥x轴于G.首先确定点F的坐标,再利用平行线分线段成比例定理解决问题即可.
【答案】解:将线段OB绕点O顺时针旋转90°得到OE.连接BE交OB′于F,作FH⊥x轴于H,B′G⊥x轴于G.
∵B(1,2),可得E(2,﹣1),
∵∠BOF=∠EOF,OB=OE,
∴BF=EF,
∴F(,),
∴OF==,OB=OB′==,
∵FH∥B′G,
∴==,
∴==,
∴OG=,B′G=,
∴B′(,)
故选:B.
【点睛】本题考查坐标与图形变化﹣旋转,等腰三角形的性质,平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,构造特殊三角形解决问题,属于中考常考题型.
8.(2019春?宛城区期末)如图,把△ABC绕顶点C按顺时针方向旋转得到△A'B'C,当A′B′⊥AC.∠A=47°,∠A'CB=128°时,∠B'CA的度数为( )
A.44° B.43° C.42° D.40°
【思路点拨】根据旋转的性质可知∠A′=∠A=47°,则∠A′CA=90°﹣47°=43°,由∠BCB′=∠A′CA=43°,则∠B′CA=∠A′CB﹣∠A′CA﹣∠BCB′可求.
【答案】解:根据旋转的性质可知∠A′=∠A=47°,
∴∠A′CA=90°﹣47°=43°.
根据旋转的性质可知旋转角相等,即∠BCB′=∠A′CA=43°,
∴∠B′CA=∠A′CB﹣∠A′CA﹣∠BCB′=128°﹣43°﹣43°=42°.
故选:C.
【点睛】本题主要考查了旋转的性质,解决这类问题要找准旋转角、以及旋转后对应的线段和角.
9.(2019?青白江区模拟)如图,△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使得DC∥AB,则∠BAE等于( )
A.30° B.40° C.50° D.60°
【思路点拨】由旋转的性质可得AD=AC,∠DAC=∠EAB,由等腰三角形的性质和三角形的内角和定理可求解.
【答案】解:如图,
∵DC∥AB,
∴∠DCA=∠CAB=70°,
∵将△ABC绕点A旋转到△AED的位置,
∴AD=AC,∠DAC=∠EAB,
∴∠ADC=∠DCA=70°
∴∠DAC=∠EAB=40°
故选:B.
【点睛】本题考查了旋转的性质,平行线的性质,熟练运用旋转的旋转是本题的关键.
10.(2019春?襄汾县期末)如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置.若四边形AECF的面积为9,BF=1,则AE的长为( )
A.3 B.4 C. D.
【思路点拨】由旋转的性质可得BF=DE=1,S△AFB=S△ADE,可求AD=3,由勾股定理可求AE的长.
【答案】解:∵把△ADE绕点A顺时针旋转90°到△ABF的位置
∴BF=DE=1,S△AFB=S△ADE,
∴S正方形ABCD=S四边形AECF=9
∴AD=3
∴AE==
故选:D.
【点睛】本题考查了旋转的性质,正方形的性质,求出AD的长是本题的关键.
11.(2019春?历下区期末)如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,则∠EAC的度数是( )
A.30° B.45° C.60° D.75°
【思路点拨】用性质的性质可知△ACE是等腰直角三角形,由此即可解决问题.
【答案】解:由题意:A,D,E共线,
又∵CA=CE,∠ACE=90°,
∴∠EAC=∠E=45°,
故选:B.
【点睛】本题考查旋转变换,等腰直角三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题.
12.(2019春?兰陵县期中)如图,△ABC绕点A旋转一定角度后得到△ADE,若BC=4,AC=3,则下列说法正确的是( )
A.DE=3 B.AE=4
C.∠ACB是旋转角 D.∠CAE是旋转角
【思路点拨】由旋转的意义可得,将△ABC绕点A逆时针旋转一个角度后得到△ADE,此时对应边为;AC=AE,AB=AD,CB=ED,旋转角为∠CAE或∠BAD,以此逐个进行判断,得出答案.
【答案】解:由旋转的性质得:DE=BC=4,故A不正确;AE=AC=3,故B不正确;旋转角是∠CAE,故D正确;∠ACB不是旋转角,故C不正确;
故选:D.
【点睛】考查旋转的性质,对应边相等、对应角相等,理解旋转角的意义等知识,掌握这些知识是前提和基础.
13.(2019春?南海区期末)如图,△ABC中,∠ACB=90°,∠ABC=22.5°,将△ABC绕着点C顺时针旋转,使得点A的对应点D落在边BC上,点B的对应点是点E,连接BE.下列说法中,正确的有( )
①DE⊥AB; ②∠BCE是旋转角; ③∠BED=30°;④△BDE与△CDE面积之比是:1.
A.1个 B.2个 C.3个 D.4个
【思路点拨】由旋转的性质可得AC=DC,BC=CE,∠ABC=∠CED=22.5°,∠BCE是旋转角,可判断①②,由等腰三角形的性质可判断③④.
【答案】解:如图,连接AD,延长ED交AB于点F,
∵将△ABC绕着点C顺时针旋转,使得点A的对应点D落在边BC上,
∴AC=DC,BC=CE,∠ABC=∠CED=22.5°,∠BCE是旋转角,
∵∠ABC+∠BAC=90°,
∴∠BAC+∠CED=90°
∴∠AFE=90°
∴DE⊥AB,
故①②正确
∵∠BCE=90°,BC=CE
∴∠BEC=45°
∴∠BED=∠BEC﹣∠CED=22.5°
故③错误
∵AC=CD,
∴AD=CD,∠DAC=∠ADC=45°
∵∠ADC=∠ABC+∠BAD
∴∠ABC=∠BAD=22.5°
∴AD=BD=CD
∴△BDE与△CDE面积之比是:1.
故④正确
故选:C.
【点睛】本题考查了旋转的性质,等腰三角形的性质,熟练运用旋转的性质是本题的关键.
14.(2019春?沙县期末)如图,在△ABC中,AB=3,AC=2,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC,则BC1的长为( )
A. B. C.4 D.6
【思路点拨】根据旋转的性质得出AC=AC1,∠BAC1=90°,进而利用勾股定理解答即可.
【答案】解:∵将△ABC绕点A逆时针旋转60°得到△AB1C1,
∴AC=AC1=2,∠CAC1=60°,
∵AB=3,AC=2,∠BAC=30°,
∴∠BAC1=90°,
∴在Rt△BAC1中,BC1==.
故选:B.
【点睛】此题考查旋转的性质,解题时注意:对应点到旋转中心的距离相等,对应点与旋转中心所连线段的夹角等于旋转角.
15.(2019春?桂林期末)如图,正方形ABCD的对角线AC与BD相交于点O.将∠COB绕点O顺时针旋转,设旋转角为α(0<α<90°),角的两边分别与BC,AB交于点M,N,连接DM,CN,MN,下列四个结论:
①∠CDM=∠COM;②CN⊥DM;③△CNB≌△DMC;④AN2+CM2=MN2;其中正确结论的个数是( )
A.1 B.2 C.3 D.4
【思路点拨】由“ASA”可证△OCM≌△OBN,可得CM=BN,∠CDM=∠BCN,由余角的性质可判断②,由点O,点M,点B,点N四点共圆可判断①,由“SAS”可证△DCM≌△CNB,由勾股定理可判断④.
【答案】解:∵四边形ABCD是正方形
∴CD=BC,BO=CO,AC⊥BD,∠ACB=∠ABD=45°
∵将∠COB绕点O顺时针旋转,
∴∠COM=∠BON,且BO=CO,∠ACB=∠ABD
∴△OCM≌△OBN(ASA)
∴CM=BN,∠CDM=∠BCN
∵∠CDM+∠CMD=90°
∴∠BCN+∠CMD=90°
∴CN⊥DM
故②正确
∵∠MON=∠ABC=90°
∴点O,点M,点B,点N四点共圆
∴∠BON=∠BMN=∠COM>∠BCN=∠CDM
故①错误
∵CM=BN,CD=BC,∠ABC=∠DCB=90°
∴△DCM≌△CNB(SAS)
故③正确
∵AB=BC,BN=CM
∴AN=BM
∵BN2+BM2=MN2,
∴AN2+CM2=MN2;
故④正确
故选:C.
【点睛】本题主要考查了旋转的性质,正方形的性质、全等三角形的判定与性质,勾股定理的综合应用,熟练掌握正方形的性质,证明三角形全等是解题的关键.
三.解答题
16.(2019?南岗区校级一模)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1(点A的对应点为A1,点B的对应点为B1,点C的对应点为C1),并写出点A1的坐标;
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2(点A1的对应点为A2,点B1的对应点为B2,点C1的对应点为C2).
【思路点拨】(1)分别作出A,B,C的对应点A1,B1,C1即可.
(2)分别作出点A1,B1,C1的对应点A2,B2,C2即可.
【答案】解:(1)△ABC关于x轴对称的△A1B1C1如图所示.
(2)△A2B2C2即为所求.
【点睛】本题考查作图﹣旋转变换,轴对称等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
17.(2019春?工业园区期末)如图,将△ABC绕点A按逆时针方向旋转,使点B落在BC边上的点D处,得△ADE若DE∥AB,∠ACB=40°,求∠DEC的度数.
【思路点拨】根据旋转的性质得到∠ADE=∠B,AB=AD,AC=AE,∠AED=∠ACD=40°,根据平行线的性质得到∠ADE=∠BAD,推出△ABD是等边三角形,△ACE是等边三角形,于是得到结论.
【答案】解:∵将△ABC绕点A按逆时针方向旋转得△ADE,
∴∠ADE=∠B,AB=AD,AC=AE,∠AED=∠ACD=40°,
∵DE∥AB,
∴∠ADE=∠BAD,
∴∠B=∠BAD,
∴BD=AD=AB,
∴△ABD是等边三角形,
∴∠BAD=60°,
∴∠CAE=60°,
∴△ACE是等边三角形,
∴∠AEC=60°,
∴∠DEC=60°﹣40°=20°.
【点睛】本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.
18.(2019春?无棣县期末)如图,在正方形ABCD中,E、F是对角线BD上两点,将△ADF绕点A顺时针旋转90°后,得到△ABM,连接EM,AE,且使得∠MAE=45°.
(1)求证:ME=EF;
(2)求证:EF2=BE2+DF2.
【思路点拨】(1)直接利用旋转的性质得出△AME≌△AFE(SAS),进而得出∠AEM=∠AEF,即可得出答案;
(2)利用(1)中所求,再结合勾股定理得出答案.
【答案】证明:(1)∵将△ADF绕点A顺时针旋转90°后,得到△ABM,
∴MB=DF,AM=AF,∠BAM=∠DAF,
∵∠EAM=45°,∠MAF=90°
∴∠FAE=45°,
∴∠MAE=∠FAE,
在△AME和△AFE中
,
∴△AME≌△AFE(SAS)
ME=EF.
(2)由(1)得△AME≌△AFE,
∴ME=EF,
∵∠ABM=∠ADF=45°,∠ABD=45°,
∴∠MBE=90°.
在Rt△MBE中,∵MB2+BE2=ME2,
又∵MB=DF,
∴EF2=BE2+DF2.
【点睛】此题主要考查了旋转的性质以及全等三角形的判定与性质和勾股定理等知识,正确得出△AQE≌△AFE(SAS)是解题关键.
19.(2019?道里区三模)如图,在△ABC中,AC=AB,把△ABC绕点A顺时针旋转得到△ADE(点B、C分别对应点D、E),BD和CE交于点F.
(1)求证:CE=BD;
(2)若AB=2,∠BAC=45°,当四边形ADFC是平行四边形时,求BF的长.
【思路点拨】(1)由旋转的性质可得AD=AB,AE=AC,∠DAE=∠BAC,由“SAS”可证△AEC≌△ADB,可得CE=BD;
(2)由平行四边形的性质可得DF=AC,AC∥BD,可得∠ABD=∠BAC=45°,可求∠BAD=90°,可得BD=AB=2,即可求BF的长.
【答案】证明:(1)∵把△ABC绕点A顺时针旋转得到△ADE
∴△ABC≌△ADE
∴AD=AB,AE=AC,∠DAE=∠BAC
∴∠DAE+∠BAE=∠BAC+∠BAE
∴∠DAB=∠EAC,
∵AB=AC
∴AD=AB=AC=AE
∵∠DAB=∠EAC,AD=AB,AC=AE
∴△AEC≌△ADB(SAS)
∴CE=BD
(2)∵四边形ADFC是平行四边形
∴DF=AC,AC∥BD
∴∠ABD=∠BAC=45°
∵AB=AD
∴∠DBA=∠BDA=45°
∴∠BAD=90°
∴BD=AB=2
∵DF=AC=AB=2
∴BF=BD﹣DF=2﹣2
【点睛】本题考查了旋转的性质,平行四边形的性质,全等三角形的判定和性质,熟练运用旋转的性质是本题的关键.
20.(2019春?商河县期中)如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°.若固定△ABC,将△DEC绕点C旋转.
(1)当△DEC统点C旋转到点D恰好落在AB边上时,如图2.
①当∠B=∠E=30°时,此时旋转角的大小为 60° ;
②当∠B=∠E=α时,此时旋转角的大小为 2α (用含α的式子表示).
(2)当△DEC绕点C旋转到如图3所示的位置时,小杨同学猜想:△BDC的面积与△AEC的面积相等,试判断小杨同学的猜想是否正确,若正确,请你证明小杨同学的猜想.若不正确,请说明理由.
【思路点拨】(1)①证明△ADC是等边三角形即可.
②如图2中,作CH⊥AD于H.想办法证明∠ACD=2∠B即可解决问题.
(2)小扬同学猜想是正确的.过B作BN⊥CD于N,过E作EM⊥AC于M,如图3,想办法证明△CBN≌△CEM(AAS)即可解决问题.
【答案】解:(1)①∵∠B=30°,∠ACB=90°,
∴∠CAD=90°﹣30°=60°,
∵CA=CD,
∴△ACD是等边三角形,
∴∠ACD=60°,
∴旋转角为60°,
故答案为60°.
②如图2中,作CH⊥AD于H.
∵CA=CD,CH⊥AD,
∴∠ACH=∠DCH,
∵∠ACH+∠CAB=90°,∠CAB+∠B=90°,
∴∠ACH=∠B,
∴∠ACD=2∠ACH=2∠B=2α,
∴旋转角为2α.
故答案为2α.
(2)小扬同学猜想是正确的,证明如下:
过B作BN⊥CD于N,过E作EM⊥AC于M,如图3,
∵∠ACB=∠DCE=90°,
∴∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3,
∵BN⊥CD于N,EM⊥AC于M,
∴∠BNC=∠EMC=90°,
∵△ACB≌△DCE,
∴BC=EC,
在△CBN和△CEM中,
∠BNC=∠EMC,∠1=∠3,BC=EC,
∴△CBN≌△CEM(AAS),
∴BN=EM,
∵S△BDC=?CD?BN,S△ACE=?AC?EM,
∵CD=AC,
∴S△BDC=S△ACE.
【点睛】本题考查旋转变换,全等三角形的判定和性质,等边三角形的判定和性质,等腰三角形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
同课章节目录
