浙教版九年级数学上册第3章 圆的基本性质3.3垂径定理同步练习题(25道题解析版)
文档属性
| 名称 | 浙教版九年级数学上册第3章 圆的基本性质3.3垂径定理同步练习题(25道题解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 453.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-22 19:40:00 | ||
图片预览

文档简介
浙教新版数学九年级上册:3.3垂径定理同步练习题
一.选择题(共7小题)
1.过⊙O内一点N的最长弦为6,最短的弦长为4,那么ON的长为( )
A. B.2 C. D.
2.圆的半径为13cm,两弦AB∥CD,AB=24cm,CD=10cm,则两弦AB,CD的距离是( )
A.7cm B.17cm C.12cm D.7cm或17cm
3.如图,已知⊙O的半径为5,弦AB=7,M是AB上任意一点,则线段OM的长不可能是( )
A.3.5 B.4.5 C.4 D.5
4.在圆柱形油槽内装有一些油,截面如图,油面宽AB为6dm,如果再注入一些油后,油面AB上升ldm,油面宽为8dm,圆柱形油槽直径MN为( )
A.6dm B.8dm C.10dm D.12dm
5.若P为半径长是6cm的⊙O内一点,OP=2cm,则过P点的最短的弦长为( )
A.12cm B.cm C.cm D.cm
6.下列命题中,正确的是( )
A.平分弦的直线必垂直于这条弦
B.垂直于弦的直线必过圆心
C.平分弦的直径必垂直于这条弦,并且平分这条弦所对的两条弧
D.垂直平分弦的直线必平分这条弦所对的弧
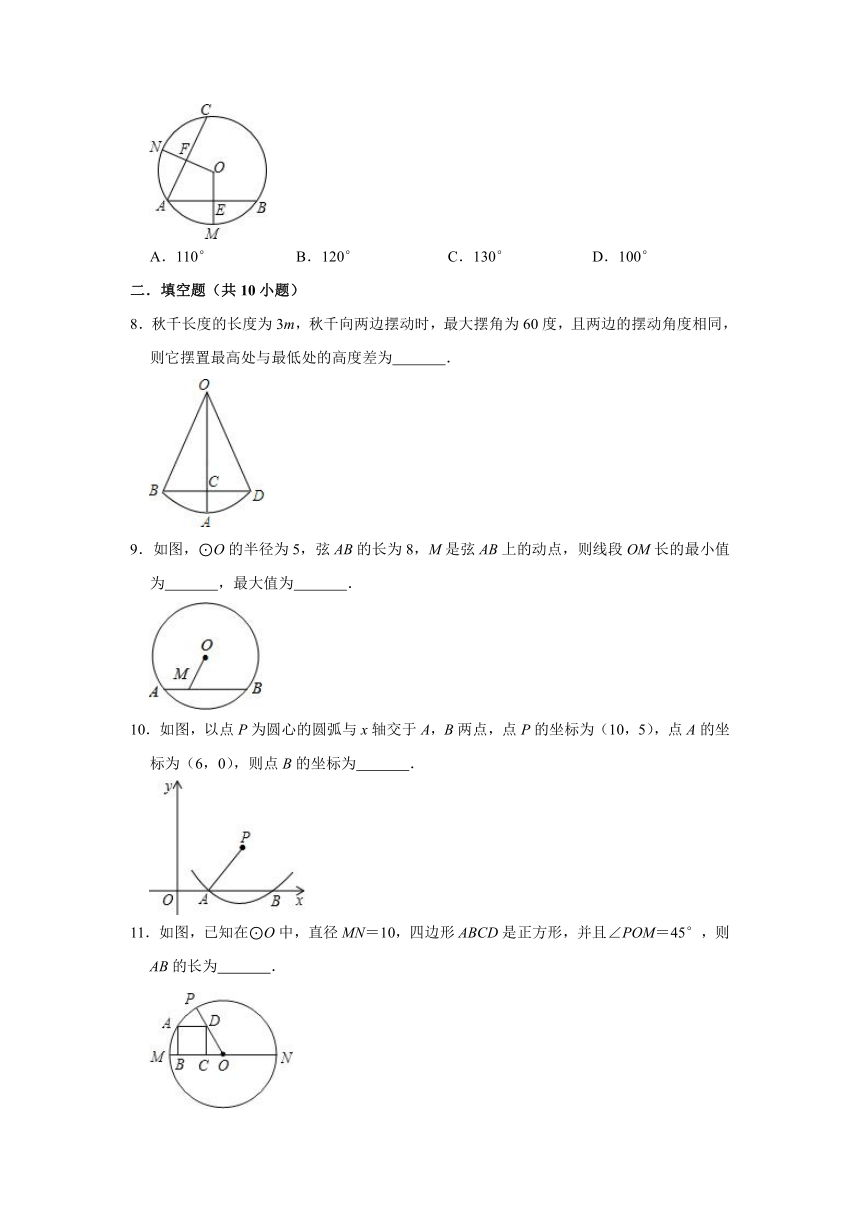
7.如图所示,⊙O的弦AB、AC的夹角为50°,MN分别为弧AB和弧AC的中点,OM、ON分别交AB、AC于点E、F,则∠MON的度数为( )
A.110° B.120° C.130° D.100°
二.填空题(共10小题)
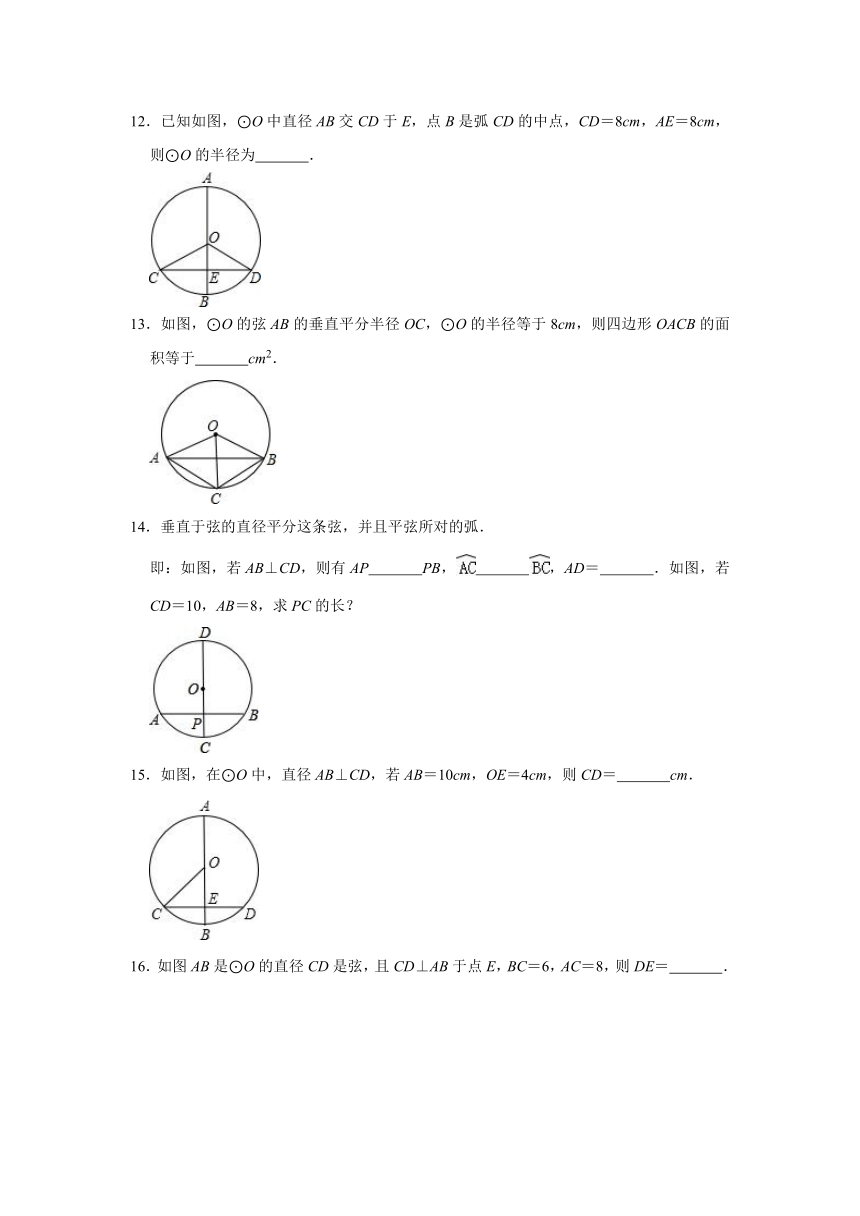
8.秋千长度的长度为3m,秋千向两边摆动时,最大摆角为60度,且两边的摆动角度相同,则它摆置最高处与最低处的高度差为 .
9.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM长的最小值为 ,最大值为 .
10.如图,以点P为圆心的圆弧与x轴交于A,B两点,点P的坐标为(10,5),点A的坐标为(6,0),则点B的坐标为 .
11.如图,已知在⊙O中,直径MN=10,四边形ABCD是正方形,并且∠POM=45°,则AB的长为 .
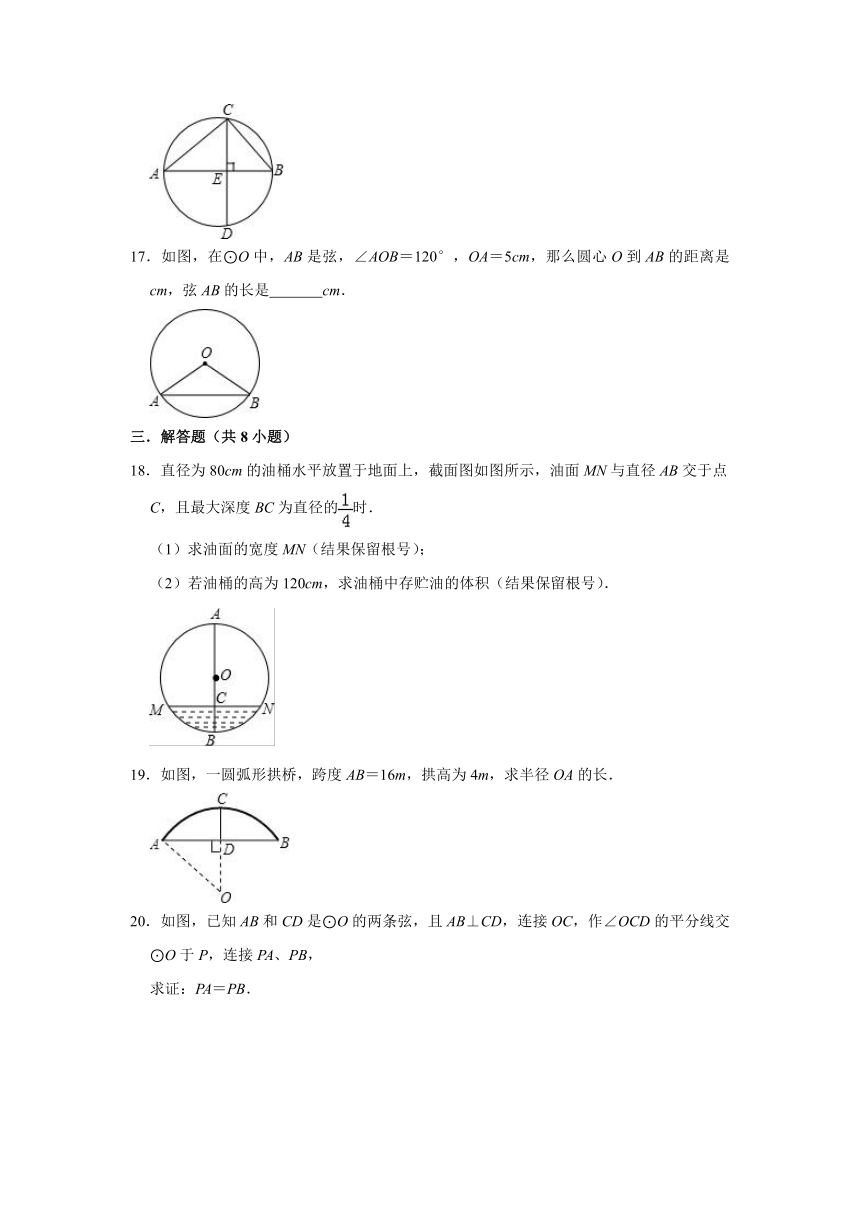
12.已知如图,⊙O中直径AB交CD于E,点B是弧CD的中点,CD=8cm,AE=8cm,则⊙O的半径为 .
13.如图,⊙O的弦AB的垂直平分半径OC,⊙O的半径等于8cm,则四边形OACB的面积等于 cm2.
14.垂直于弦的直径平分这条弦,并且平弦所对的弧.
即:如图,若AB⊥CD,则有AP PB, ,AD= .如图,若CD=10,AB=8,求PC的长?
15.如图,在⊙O中,直径AB⊥CD,若AB=10cm,OE=4cm,则CD= cm.
16.如图AB是⊙O的直径CD是弦,且CD⊥AB于点E,BC=6,AC=8,则DE= .
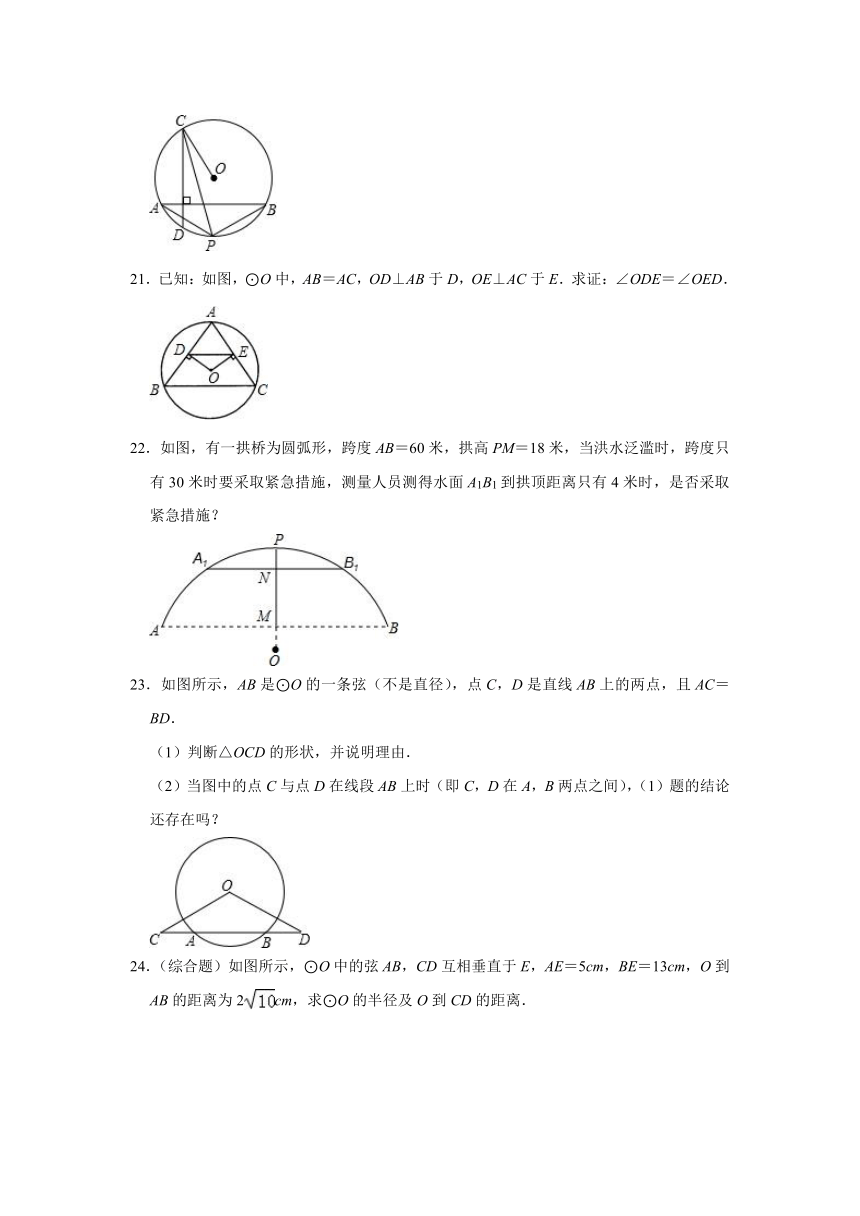
17.如图,在⊙O中,AB是弦,∠AOB=120°,OA=5cm,那么圆心O到AB的距离是 cm,弦AB的长是 cm.
三.解答题(共8小题)
18.直径为80cm的油桶水平放置于地面上,截面图如图所示,油面MN与直径AB交于点C,且最大深度BC为直径的时.
(1)求油面的宽度MN(结果保留根号);
(2)若油桶的高为120cm,求油桶中存贮油的体积(结果保留根号).
19.如图,一圆弧形拱桥,跨度AB=16m,拱高为4m,求半径OA的长.
20.如图,已知AB和CD是⊙O的两条弦,且AB⊥CD,连接OC,作∠OCD的平分线交⊙O于P,连接PA、PB,
求证:PA=PB.
21.已知:如图,⊙O中,AB=AC,OD⊥AB于D,OE⊥AC于E.求证:∠ODE=∠OED.
22.如图,有一拱桥为圆弧形,跨度AB=60米,拱高PM=18米,当洪水泛滥时,跨度只有30米时要采取紧急措施,测量人员测得水面A1B1到拱顶距离只有4米时,是否采取紧急措施?
23.如图所示,AB是⊙O的一条弦(不是直径),点C,D是直线AB上的两点,且AC=BD.
(1)判断△OCD的形状,并说明理由.
(2)当图中的点C与点D在线段AB上时(即C,D在A,B两点之间),(1)题的结论还存在吗?
24.(综合题)如图所示,⊙O中的弦AB,CD互相垂直于E,AE=5cm,BE=13cm,O到AB的距离为2cm,求⊙O的半径及O到CD的距离.
25.在直径为1米的圆柱形油槽内装入一些油后,截面如图所示,若油面宽AB=0.6米,求油的最大深度.
浙教新版数学九年级上册:3.3垂径定理同步练习题
参考答案
一.选择题(共7小题)
1.过⊙O内一点N的最长弦为6,最短的弦长为4,那么ON的长为( )
A. B.2 C. D.
【解答】解:如图所示,则直径AB是过点N的最长的弦.
过N点作弦CD⊥AB,则CD是过N的最短的弦.
连接OC.
∵ON⊥CD,
∴CN=CD=2,
又OC=3,
∴ON=.
故选:C.
2.圆的半径为13cm,两弦AB∥CD,AB=24cm,CD=10cm,则两弦AB,CD的距离是( )
A.7cm B.17cm C.12cm D.7cm或17cm
【解答】解:作OE⊥CD,
∵AB∥CD,∴OE⊥AB,
当两弦在圆心的同侧时,
已知CD=10cm,
∴由垂径定理得DE=5.
∵OD=13,
∴利用勾股定理可得:OE=12.
同理可求OF=5,
∴EF=7.
当两弦在圆心的两侧时,
EF=OE+OF=17.
故选:D.
3.如图,已知⊙O的半径为5,弦AB=7,M是AB上任意一点,则线段OM的长不可能是( )
A.3.5 B.4.5 C.4 D.5
【解答】解:连接OA,过点O作OD⊥AB于点D,当点M与点A重合时OM最长,当点M于点D重合时OM最短,
∵OD⊥AB,AB=7,
∴AD=AB=,
∴OD===,
∴≤OM≤5.
∵>=3.5,
∴A不合题意.
故选:A.
4.在圆柱形油槽内装有一些油,截面如图,油面宽AB为6dm,如果再注入一些油后,油面AB上升ldm,油面宽为8dm,圆柱形油槽直径MN为( )
A.6dm B.8dm C.10dm D.12dm
【解答】解:根据题意画出图形,如图所示,EF=1dm,AB=6dm,CD=8dm,设圆的半径为r,
∵OE⊥CD,OF⊥AB,
∴CE=DE=4dm,AF=BF=3dm,
在Rt△OCE和△OAF中,
根据勾股定理得:OE==,OF==,
∴OE﹣OF=1,即﹣=1,
=+1,
两边平方得,r2﹣9=r2﹣16+2+1,
=3,
两边平方得,r2﹣16=9,
r2=25,
解得:r=5,
则圆柱形油槽直径MN为10dm.
故选:C.
5.若P为半径长是6cm的⊙O内一点,OP=2cm,则过P点的最短的弦长为( )
A.12cm B.cm C.cm D.cm
【解答】解:如图,∵OA=6cm,OP=2cm,
∴AP===4cm,
∴AB=8cm,
∴过P的最短的弦长等于8cm,
故选:D.
6.下列命题中,正确的是( )
A.平分弦的直线必垂直于这条弦
B.垂直于弦的直线必过圆心
C.平分弦的直径必垂直于这条弦,并且平分这条弦所对的两条弧
D.垂直平分弦的直线必平分这条弦所对的弧
【解答】解:A、过弦的中点的直线都是平分线的直线,有无数条,所以平分弦的直线不一定垂直于这条弦;故A错误.
B、垂直于弦的直线有无数条,所以垂直于弦的直线不一定过圆心,垂直平分弦的直线过圆心;故B错误.
C、根据垂径定理的推论,平分弦(不是直径)的直径必垂直于这条弦,因为任意两条直径互相平分,但不一定垂直;故C错误.
D、垂直平分弦的直线必过圆心,并且平分这条弦所对的弧;故D正确.
故选:D.
7.如图所示,⊙O的弦AB、AC的夹角为50°,MN分别为弧AB和弧AC的中点,OM、ON分别交AB、AC于点E、F,则∠MON的度数为( )
A.110° B.120° C.130° D.100°
【解答】解:∵M、N分别为弧AB和弧AC的中点,
∴OF⊥AC,OE⊥AB,
∴∠OFA=∠OEA=90°,
∴在四边形OEAF中,∠MON=360°﹣∠OFA﹣∠OEA﹣∠A=360°﹣90°﹣90°﹣50°=130°.
故选:C.
二.填空题(共10小题)
8.秋千长度的长度为3m,秋千向两边摆动时,最大摆角为60度,且两边的摆动角度相同,则它摆置最高处与最低处的高度差为 (3﹣)米 .
【解答】解:∵最大摆角为60度,
∴∠BOD=60°,
∴∠BOA=∠DOA=30°.
∵OB=OD=3米,
∴BC=OB=米,
∴OC===(米),
∴AC=OA﹣AC=(3﹣)米.
故答案为:(3﹣)米.
9.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM长的最小值为 3 ,最大值为 5 .
【解答】解:如图所示,
过O作OM′⊥AB,连接OA,
∵过直线外一点与直线上的所有连线中垂线段最短,
∴当OM于OM′重合时OM最短,
∵AB=8,OA=5,
∴AM′=×8=4,
∴在Rt△OAM′中,OM′===3,
∴线段OM长的最小值为3,最大值为5.
故答案为:3,5.
10.如图,以点P为圆心的圆弧与x轴交于A,B两点,点P的坐标为(10,5),点A的坐标为(6,0),则点B的坐标为 (14,0) .
【解答】解:过点P作PM⊥AB于M,则M的坐标是(10,0).
又∵A的坐标为(6,0),
∴OA=6,AM=OM﹣OA=10﹣6=4,
∵A,B两点一定关于PM对称.
∴MB=AM=4,
∴OB=OM+MB=10+4=14,
∴点B的坐标是(14,0).
故答案为:(14,0).
11.如图,已知在⊙O中,直径MN=10,四边形ABCD是正方形,并且∠POM=45°,则AB的长为 .
【解答】解:∵∠POM=45°,∠DCO=90°,
∴∠DOC=∠CDO=45°,
∴△CDO为等腰直角三角形,
∴CO=CD.
连接OA,则△OAB是直角三角形,
∵四边形ABCD是正方形,
∴AB=BC=CD=CO,BO=BC+CO=BC+CD=2AB,
∴AB2+OB2=52,即AB2+(2AB)2=52,
∴AB的长为.
故答案为:.
12.已知如图,⊙O中直径AB交CD于E,点B是弧CD的中点,CD=8cm,AE=8cm,则⊙O的半径为 5 .
【解答】解:设⊙O的半径为rcm,
∵点B是弧CD的中点,CD=8cm,AB是直径,
∴AB⊥CD,CE=ED=CD=4cm,
在Rt△COE中,由勾股定理得:OC2=CE2+OE2,
r2=42+(8﹣r)2,
解得r=5.
故答案为:5.
13.如图,⊙O的弦AB的垂直平分半径OC,⊙O的半径等于8cm,则四边形OACB的面积等于 cm2.
【解答】解:∵AB垂直平分OC,
∴OA=AC,又半径OA=OC,
∴△OAC为等边三角形,四边形OACB为菱形,
∵OA=OC=8,
∴AB=8,S四边形OACB=×OC×AB=×8×8=32.
故答案为:32.
14.垂直于弦的直径平分这条弦,并且平弦所对的弧.
即:如图,若AB⊥CD,则有AP = PB, = ,AD= BD .如图,若CD=10,AB=8,求PC的长?
【解答】解:∵AB⊥CD,
∴由垂径定理,可得AP=BP,=,AD=BD,
连接OA,∵AB⊥CD,CD=10,AB=8,
∴AP=4,OA=5,
∴由勾股定理得,OP=3,
∴PC=OC﹣OP=5﹣3=2.
15.如图,在⊙O中,直径AB⊥CD,若AB=10cm,OE=4cm,则CD= 6 cm.
【解答】解:由题意得:OC=5,OE=4
∴Rt△OCE中可求得CE==3cm
根据垂径定理可得:CD=2CE=6cm.
16.如图AB是⊙O的直径CD是弦,且CD⊥AB于点E,BC=6,AC=8,则DE= .
【解答】解:∵AB是⊙O的直径CD是弦,且CD⊥AB于点E
∴CE=DE,AC⊥BC
∵BC=6,AC=8
∴AB=10
∵S△ABC=×AC×BC=×CE×AB
∴AC×BC=CE×AB
∴CE==
∴DE=CE=
故此题应该填.
17.如图,在⊙O中,AB是弦,∠AOB=120°,OA=5cm,那么圆心O到AB的距离是 cm,弦AB的长是 5 cm.
【解答】解:过O作OC⊥AB交AB于C点,如右图所示:
由垂径定理可知,OC垂直平分AB,
∵OA=OB,∠AOB=120°
∴∠OAB=30°
∴OC=OA=cm
∴由勾股定理可得:AC=cm
∴AB=5cm
故此题应该填,5.
三.解答题(共8小题)
18.直径为80cm的油桶水平放置于地面上,截面图如图所示,油面MN与直径AB交于点C,且最大深度BC为直径的时.
(1)求油面的宽度MN(结果保留根号);
(2)若油桶的高为120cm,求油桶中存贮油的体积(结果保留根号).
【解答】解:(1)如图,连接OM,
∵AB=80cm,BC为直径的,
∴OM=OB=40cm,BC=20cm,
∴OC=20cm,
∴MC=cm,
∴MN=2CM=40cm;
(2)∵OC=20cm,OM=40cm,
∴sin∠OMC=,
∴∠OMC=30°,
∴∠MOC=60°,
∴∠MON=120°,
∴阴影部分的面积是:=,
∵油桶的高为120cm,
∴油桶中存贮油的体积是:()×120=64000π﹣48000,
即油桶中存贮油的体积是(64000π﹣48000)cm3.
19.如图,一圆弧形拱桥,跨度AB=16m,拱高为4m,求半径OA的长.
【解答】解:∵AB=16m,OC⊥AB,
∴AD=AB=8m,
设OA=r,则OD=r﹣4,
在Rt△AOD中,OA2=AD2+OD2,即r2=82+(r﹣4)2,解得r=10m,即半径OA的长是10m.
20.如图,已知AB和CD是⊙O的两条弦,且AB⊥CD,连接OC,作∠OCD的平分线交⊙O于P,连接PA、PB,
求证:PA=PB.
【解答】证明:∵OC=OP,
∴∠1=∠2.
∵CP平分∠OCD,
∴∠2=∠3,
∴∠3=∠1,
∴CD∥OP,
∵CD⊥AB,
∴OP⊥AB.
∴=,
∴PA=PB.
21.已知:如图,⊙O中,AB=AC,OD⊥AB于D,OE⊥AC于E.求证:∠ODE=∠OED.
【解答】解:连接OA并延长交BC于点F,
∵⊙O是△ABC的外接圆,
∴点O是△ABC的外心,
∵AB=AC,
∴AF是BC的垂直平分线,
∴∠BAF=∠CAF,
∵OD⊥AB,OE⊥AC,
∴OD、OE分别是AB、AC的垂直平分线,
∵AB=AC,
∴AD=AE,
在Rt△AOD与Rt△AOE中,
,
∴Rt△AOD≌Rt△AOE,
∴OD=OE,
∴△ODE是等腰三角形,
∴∠ODE=∠OED.
22.如图,有一拱桥为圆弧形,跨度AB=60米,拱高PM=18米,当洪水泛滥时,跨度只有30米时要采取紧急措施,测量人员测得水面A1B1到拱顶距离只有4米时,是否采取紧急措施?
【解答】解:连接OA、OA1,如下图所示:
由题可得:AB=60m,PM=18m,PN=4m,OA=OA1=OP=R
OP⊥AB,OP⊥A1B1
由垂径定理可得:AM=MB=30m
在Rt△AMO中,由勾股定理可得:
AO2=AM2+MO2
即R2=302+(R﹣18)2
解得R=34m
∵PN=4m,OP=R=34m
∴ON=30m
在Rt△ONA1中,由勾股定理可得:
A1N2=A1O2﹣ON2
可得A1N=16m
故A1B1=32m>30m
故不用采取紧急措施.
23.如图所示,AB是⊙O的一条弦(不是直径),点C,D是直线AB上的两点,且AC=BD.
(1)判断△OCD的形状,并说明理由.
(2)当图中的点C与点D在线段AB上时(即C,D在A,B两点之间),(1)题的结论还存在吗?
【解答】解:(1)△OCD是等腰三角形
如左图所示,过点O作OM⊥AB,垂足为M,则有MA=MB
又AC=BD
∴AC+MA=BD+MB
即CM=DM
又OM⊥CD,即OM是CD的垂直平分线
∴OC=OD
∴△OCD为等腰三角形
(2)当点C,D在线段AB上时,如右图所示
同(1)题作OM⊥AB,垂足为M
由垂径定理,得AM=BM
又AC=BD
∴CM=AM﹣AC=BM﹣BD=MD
∴OC=OD
∴△OCD为等腰三角形.
24.(综合题)如图所示,⊙O中的弦AB,CD互相垂直于E,AE=5cm,BE=13cm,O到AB的距离为2cm,求⊙O的半径及O到CD的距离.
【解答】解:AB=AE+BE=5+13=18(cm),
连接OB,过O作OM⊥AB,
∴AM=AB=9(cm),
又∵OM=2(cm),
∴在Rt△OBM中,
BO====11cm,
ON=EM=AM﹣AE=9﹣5=4(cm).
25.在直径为1米的圆柱形油槽内装入一些油后,截面如图所示,若油面宽AB=0.6米,求油的最大深度.
【解答】解:连接OA.
∵OA=OD=0.5米,AC=AB=0.3米
∴OC2=OA2﹣AC2
∴OC==0.4米
∴CD=OD﹣OC=0.5﹣0.4=0.1米
故油的最大深度是0.1米.
同课章节目录
